一类具有修正的Leslie-Gower功能反应的生态-流行病模型
2022-07-07周学勇刘爽李永凤
周学勇, 刘爽, 李永凤
(1.信阳师范学院数学与统计学院, 河南信阳 464000;2.郑州轻工业大学数学与信息科学学院, 河南郑州 450001)
1.引言
结合传染病动力学[1]和种群动力学[2]的生态-流行病模型是探究疾病在种群内传播和发展规律的重要工具[3−4].本文研究一类具有修正的Leslie-Gower功能反应的生态流行病模型:
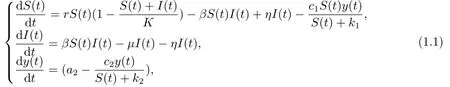
其中S(t), I(t)分别表示食饵中易感者和染病者在t时刻的密度, y(t)表示t时刻捕食者的密度.参数β, r, µ, η, a2, c1, c2, K, k1和k2均为正常数.β表示传染率, r表示食饵易感者的内禀增长率, K为食饵的环境容纳量, µ表示染病食饵的死亡率, η为恢复率, a2为捕食者的内禀增长率,c1为易感食饵的平均被捕获率, c2为捕食者的平均减少率, k1(k2)为环境对易感食饵(捕食者)提供保护的程度.
系统(1.1)的初值条件为
2.系统(1.1)的动力学性质
定理2.1系统(1.1)满足初始条件(1.2)的解是正不变的.
证因为所以系统(1.1)满足初始条件(1.2)的解是正不变的.
定理2.2系统(1.1)满足初始条件(1.2)的解满足
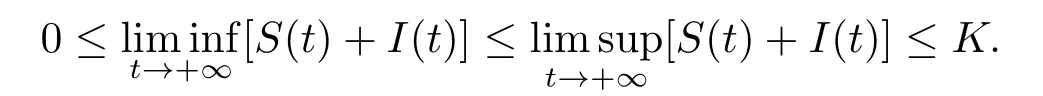
证分两种情形去证.
(I) 当初始条件S(0)+I(0)≥K时:
若S(t)+I(t)≥K对任意的t ≥0均成立, 由系统(1.1)的前两个方程知, 对所有的t ≥0有


假设ζ >K, 因为S(t)+I(t)满足Barbalat引理[5], 所以

显然构成矛盾.所以假设ζ >K不成立, 故有
若对任意的t ≥0, S(t)+I(t)≥K不成立, 则存在t0≥0, 在第一个时间有S(t0)+I(t0)=K.由系统(1.1)的前两个方程得
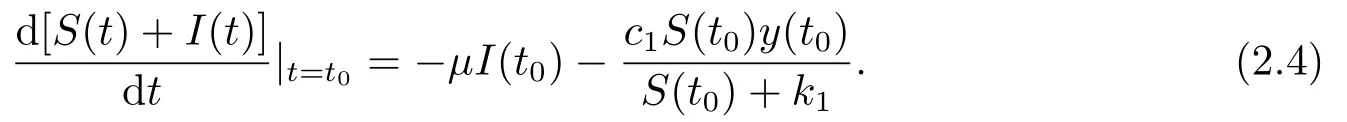
这意味着, 一旦S(t)+I(t)进入区间(0,K), 那么对所有的t ≥t0它将仍然有界.即: 对所有的t ≥t0有S(t)+I(t)≤K.
(II) 当S(0)+I(0) ≤K时, 利用(I)的相似的推导过程可知, 对任意的t ≥0, S(t)+I(t) ≤K成立.
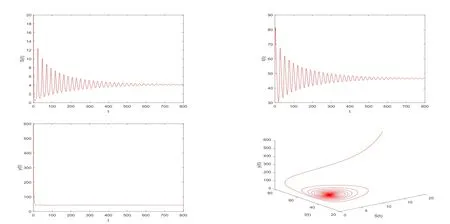
定理2.3存在M >0, 使得对系统(1.1)的任意解(S(t),I(t),y(t))有: 对充分大的t, y(t) 证由定理2.2知, 对满足S(0)+I(0)≥K的初值(S(0),I(0),y(0)), 存在t0>0有 定理2.4平衡点E0(0,0,0)是不稳定的. 证系统(1.1)在E0(0,0,0)处的雅克比矩阵为 显然, E0(0,0,0)是不稳定的. 定理2.5平衡点E1(K,0,0)是不稳定的. 证系统(1.1)在E1(K,0,0)处的雅克比矩阵为 显然, E1(K,0,0)是不稳定的. 易知, 在E3(S3,I3,0)处有特征值为λ3=a2>0.所以, E3(S3,I3,0)是不稳定的. 下面研究正平衡点的稳定性. 证当βKrc2(k1β+η) > βKc1a2(µ+η+k2β)+c2r(µ+η+k1β) 时, 系统(1.1)存在正平衡点E∗(S∗,I∗,y∗).系统(1.1)在E∗(S∗,I∗,y∗)处的雅克比矩阵为 特征方程为 由定理2.8的条件知b1>0且b1b2−b3>0.利用Hurwitz判据[7]知, 特征方程的所有特征根具有负实部, 从而平衡点E∗(S∗,I∗,y∗)是局部渐近稳定的. 为了验证理论结果的正确性, 利用MATLAB 2018a对系统(1.1)进行数值模拟. 1)取参数值r = 1,β = 0.02,K = 1000,µ = 0.08,η = 0.002,c1= 0.0085,c2= 0.25,k1= 5,k2= 50,a2= 0.2, 初值为S(0) = 20,I(0) = 60,y(0) = 600.系统(1.1)存在正平衡点E∗(4.1,46.58075943,43.28), 定理2.8的条件是满足的, 平衡点E∗(4.1,46.58075943,43.28)是局部渐近稳定的(见图1). 图1 系统(1.1)的正平衡点是渐近稳定的 2)取参数值r = 1,β = 0.02,K = 1000,µ = 0.08,η = 0.002,c1= 0.0085,c2= 0.25,k1= 5,k2= 50,a2= 2, 初值为S(0) = 20,I(0) = 60,y(0) = 600.系统(1.1)存在正平衡点E∗(4.1,28.84314722,432.8), 定理2.9的条件是满足的, 平衡点E∗(4.1,28.84314722,432.8)是不稳定的, 系统产生周期解(见图2). 图2 系统(1.1)的正平衡点是不稳定的 3)设a2为分支参数, 取参数值r = 1,β = 0.02,K = 1000,µ = 0.08,η = 0.002,c1=0.0085,c2=0.25, k1=5,k2=50, 画出Hopf分支图(见图3). 图3 Hopf分支图 本文提出并分析了一类具有修正的Leslie-Gower功能反应的生态流行病模型.首先, 我们得到解的正性和有界性,计算出模型的平衡点.其次, 利用Hurwitz判据得到了非负平衡点的局部渐近稳定性.最后, 应用常微分方程定性与稳定性方法, 得到了系统(1.1)从正平衡点分叉出周期解的条件.由数值结果可以看出当参数a2通过临界值a2=时, 系统(1.1)的正平衡点E∗(S∗,I∗,y∗)失去稳定性, 经历Hopf分支, 分支出周期解.
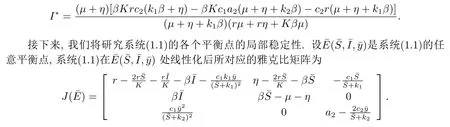
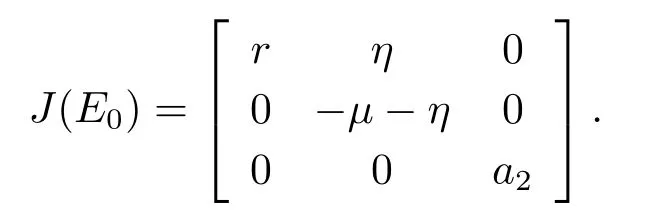
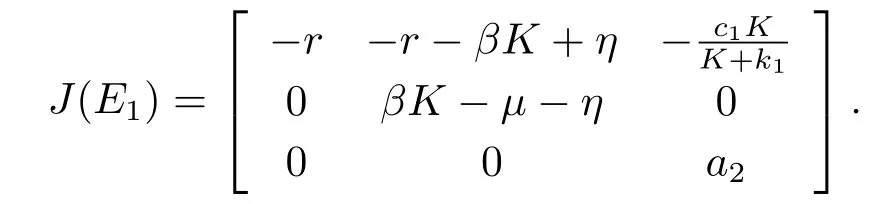

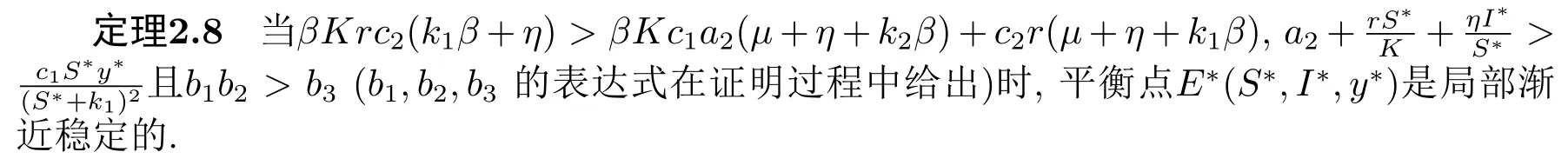

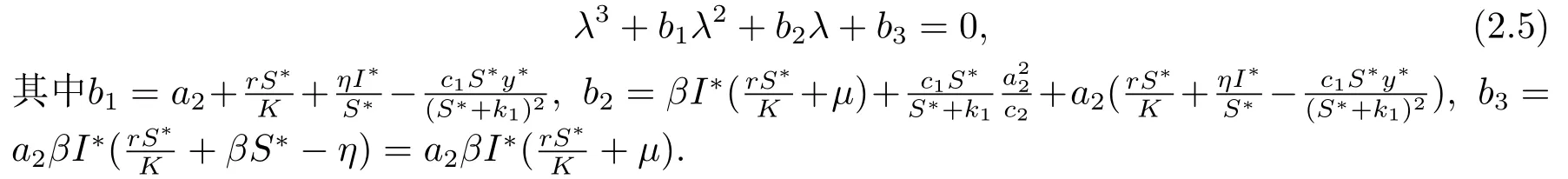

3.数值模拟


4.结论
