气固流化系统多尺度跨流域EMMS建模
2022-07-06胡善伟刘新华
胡善伟,刘新华
(中国科学院过程工程研究所,多相复杂系统国家重点实验室,北京 100190)
引 言
气固流化床内的气体、颗粒与壁面之间的相互作用导致该类系统通常呈现复杂的时空多尺度结构。随着流化气速从低到高的变化,气固系统可能会依次出现鼓泡、湍动、快速流态化以及稀相输送等跨流域流动特征[1]。在系统内部,局部非均匀性表现为气泡和团聚物的动态生成和湮灭,具有时间相依性;而整体非均匀性则表现为反应器在轴向和径向呈现有序分布的特征,具有空间相依性[1]。介尺度结构被认为是流化床反应器内多尺度非均匀性产生的根源,但目前人们对其认识程度仍不能满足实际工艺设计的需要。深入理解气固两相流介尺度动态结构特性是流化床反应器定量放大和优化设计的基础和前提。
针对气固流态化系统,无论是颗粒解析的直接数值模拟(DNS)或是流体解析的离散颗粒模型(DPM),均由于计算量巨大而难以应用于工业尺度反应器的模拟和优化。因此,基于粗粒化(coarsegrained)的离散颗粒模拟和基于粗网格(coarsegrid)的连续介质模拟仍然是现阶段主要的工业数值模拟策略。粗网格处理带来的显著问题是平均方法的失效,此时必须考虑非解析的亚网格结构对相间作用力和固相应力等本构关系的贡献[2-3],且相间曳力关系的合理构建是模拟取得成功的关键[2-6]。目前主要有三种相间曳力建模方法。(1)经验参数修正法[5-8]。通过对比实验和模拟数据,逆推出曳力系数的修正关系。例如,根据实验获得的最小流化速度及空隙率对传统均匀曳力模型进行校正[7];或采用恒定的团聚物直径(dcl)替代均匀曳力模型中的单颗粒直径(dp)来计算实际曳力系数[8]等。这类方法的主要缺点是缺乏对物理机制的分析,因而模型的可拓展性较差。(2)滤波函数法[3,9-15]。通过滤波函数对守恒方程各项进行卷积计算,以获得空间平均化的控制方程。滤波方程产生的余项来源于局部非均匀结构,需要采用亚网格模型进行封闭。以曳力系数βe(x1,x2,…)为例,一般可通过高分辨率的连续介质模拟、离散颗粒模拟或直接数值模拟获得的数据进行关联[9-15]。根据研究体系或选择参量集xi的不同,众多的βe(x1,x2,…)关联函数被相继提出。虽然它们最终形式差别很大,但一般均是滤波特征尺寸、固相分率、滑移速度等变量的函数[9-17]。近期还进一步在模型中考虑了材料性质、各向异性、压力梯度等因素的影响[18-20]。如何选择合适的标记参量(marker)组合是目前研究的热点之一[20-21]。与传统滤波方法不同,基于湍流的建模方法则是在质量和动量守恒方程的基础上严格推导本构关系[22-23],并通过对滤波余项的权重分析简化封闭关系的表达。(3)介尺度结构建模法[24-31]。通过在亚网格尺度上对局部非均匀流动结构进行分解,以气泡或团聚物为研究对象建立一系列守恒关系,并在附加约束条件下通过解析求解或数值求解方法获得曳力系数的显式表达。典型的代表是能量最小多尺度(EMMS)曳力模型[25-26]。它将系统分解为稀密两相并分别建立质量和动量守恒方程,进一步引入团聚物方程和稳定性约束条件,实现模型的封闭和数值求解[1,27]。
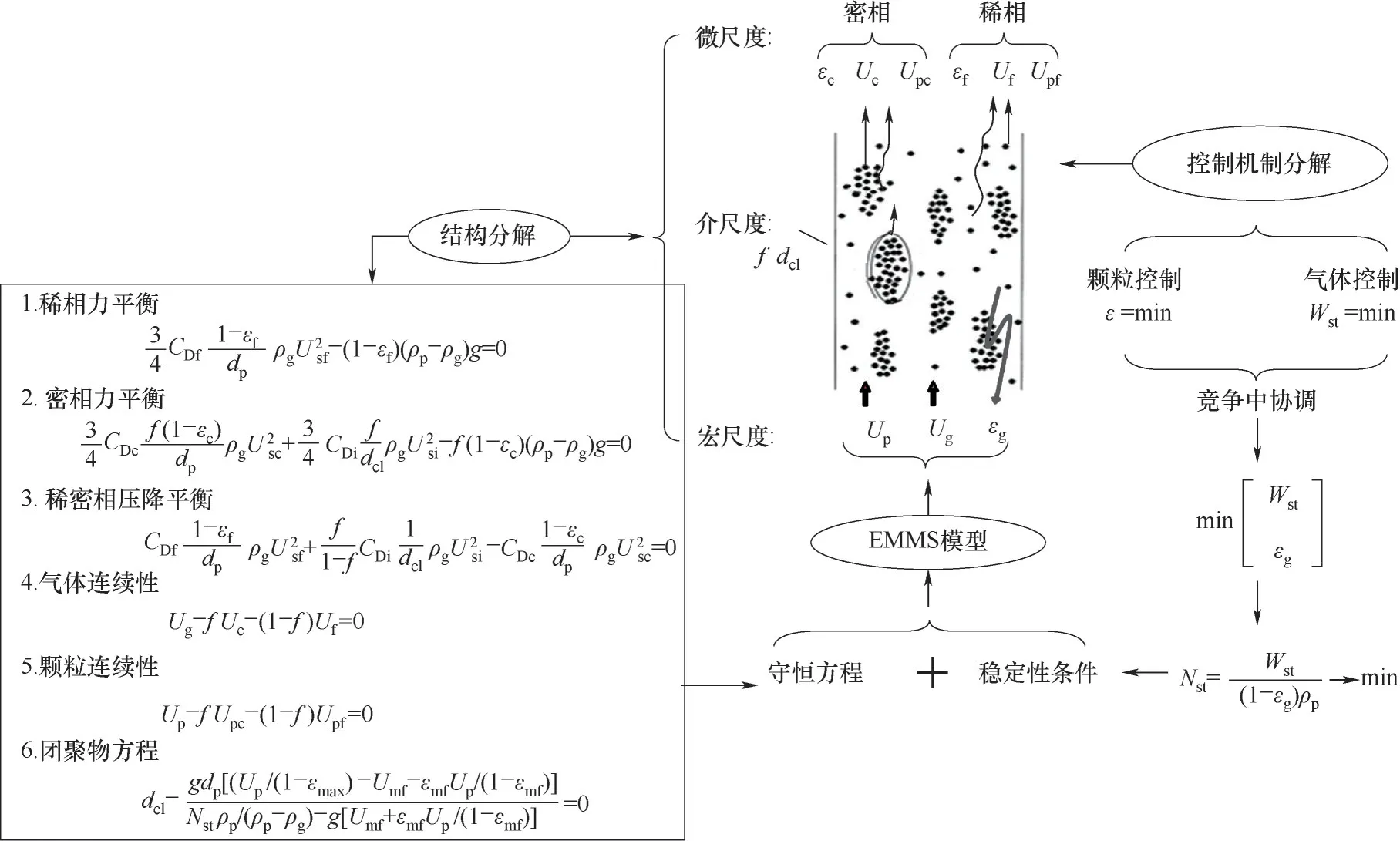
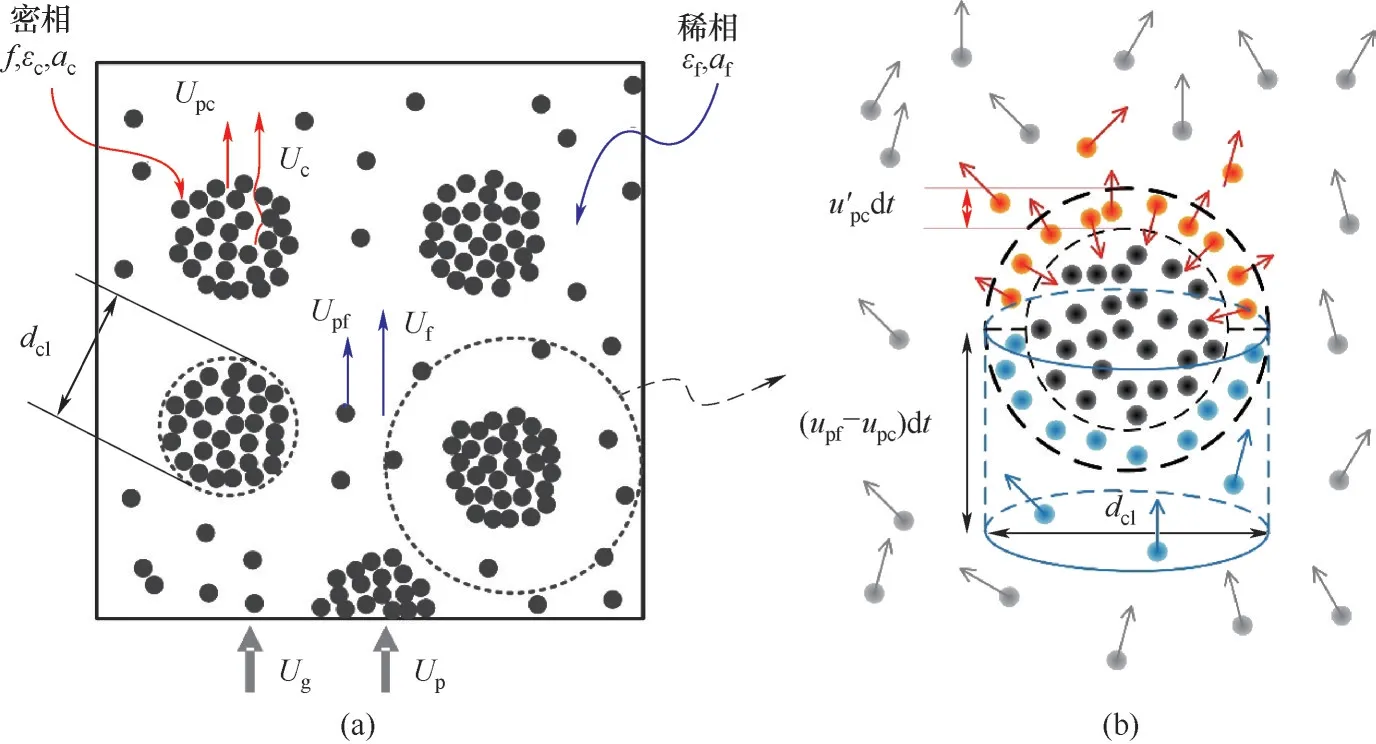
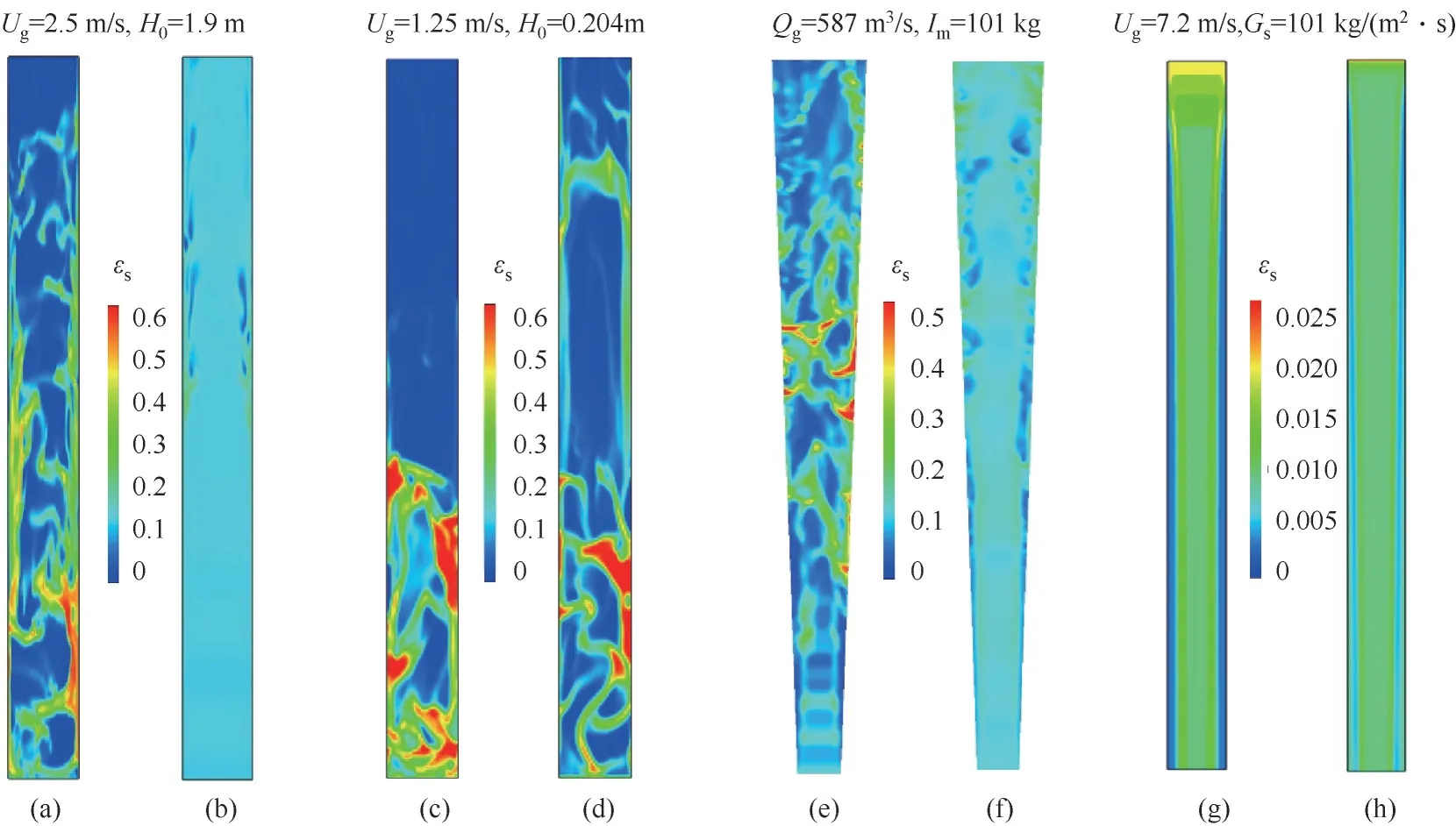
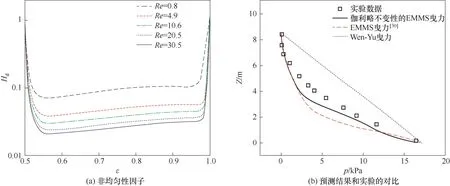
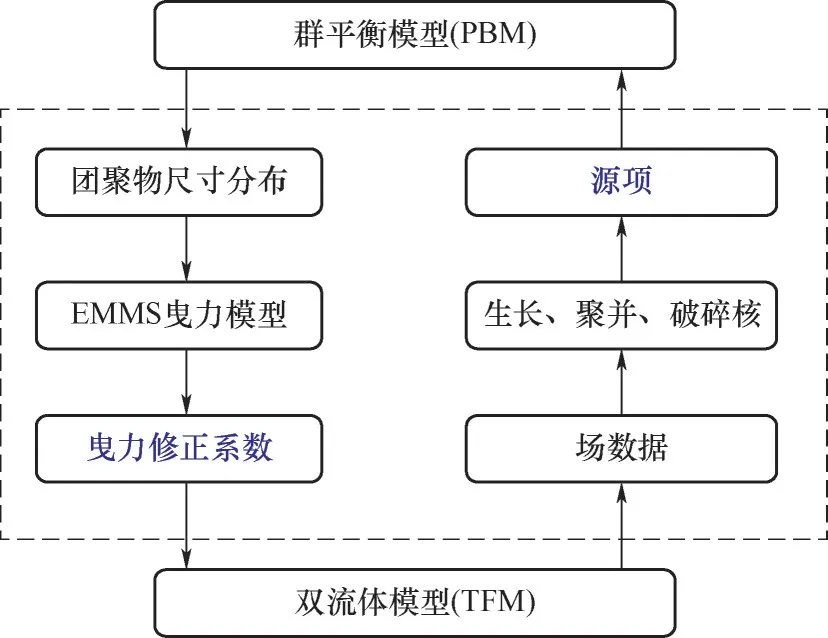
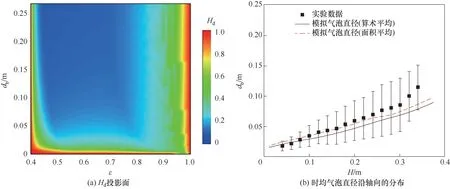
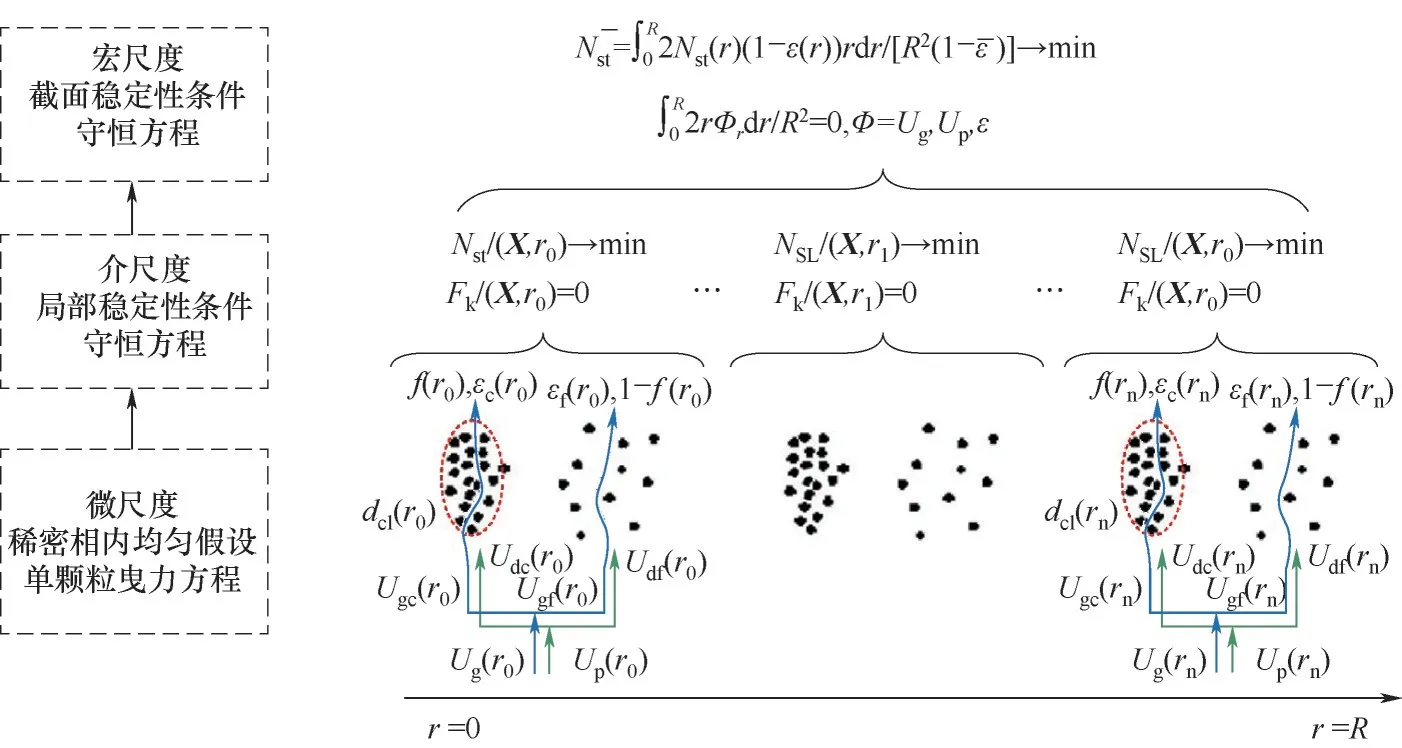
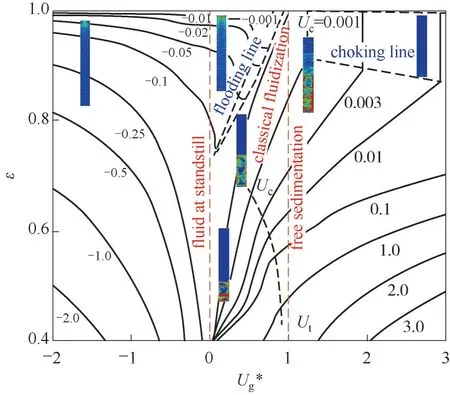
与经验方法及滤波模型不同,EMMS 模型通过量化局部非均匀结构来更直接地表征操作条件或流域变化时局部介尺度结构的演变及其对曳力的影响。EMMS模型的提出最初是为了计算快速流化床的整体非均匀结构。为了与计算流体动力学(CFD)相结合,Yang 等[26]在EMMS 模型中引入了颗粒加速度并将其应用于计算网格,从而给出了一种基于结构的EMMS 曳力系数表达式。此后,该思想被研究者广泛采用,许多改进模型被相继提出以适应更广泛的操作条件[28-37]。由于原模型中团聚物方程在低颗粒通量、强惯性力和负颗粒速度情况下并不适用(可能导致dcl 尽管EMMS模型有效考虑了局部非均匀结构对曳力本构关系的影响,但既往研究大多围绕静态的气泡和团聚物建立模型,网格内介尺度结构特征在特定操作参数和局部空隙率情况下为一定值。这样的处理方式忽略了气泡和团聚物动态演化的历史信息,很大可能导致计算网格内实际的介尺度结构信息和EMMS 预测值不匹配,因此有必要在模型中进一步引入时间变量并考虑气泡和团聚物的时空动态演化。群平衡模型(PBM)考虑了离散相的聚并破碎动力学对数密度函数的影响,已经被广泛应用于多相体系中离散相尺寸分布的时空演化特征表征[59-61]。Hu 等[62-63]通过量化稀密相质量交换建立了团聚物的连续生长模型以及低通量床中的团聚物群平衡方程,并在此基础上完善了连续介质模型、EMMS 曳力和群平衡模型的耦合框架,随后还拓展了PBM 和EMMS 耦合模型在鼓泡流化床中的应用。由于考虑了介尺度结构时空动态演化行为对局部气泡和团聚物尺寸分布的影响,所以PBM 模型的引入使得EMMS 曳力的修正结果更加可靠。 计算流体动力学模拟方法在被应用于工业反应器时可能会难以兼顾效率、精度和成本,但通过优化模拟初场、从特定的整体分布开始迭代可以改善上述问题[64-65]。一方面,相对颗粒均匀分布和紧密堆积的初始状态,通过宏尺度模型对拟稳态流场进行预测无疑更符合实际工况[30]。另一方面,人们有时更关注反应器在不同操作条件下的整体表现,采用大批量的数值模拟成本高昂且效率低下,此时稳态建模也可以为反应器的设计优化提供直接依据[66-70]。然而,气固流化床操作方式多变,且伴随着状态多值性和流域转变等复杂的非线性跨流域特征。随操作气速的变化,反应器内的气固流动还可能经历从移动床到快速床等连续演化过程。这些特征给流化床反应器的宏尺度建模带来了挑战[1]。经验的稳态模型往往很难捕捉流域转变过程中出现的“噎塞”和“液泛”等跨流域特征,但EMMS 思想为气固系统的跨流域统一建模提供了理论基础[65]。Hu等[30,67]通过考虑提升管反应器内颗粒加速效应和壁面的影响,在局部和全局稳定性条件的约束下将EMMS模型进行了轴径向二维扩展。通过分析不同流域条件下的控制机制及稳定性条件表达,相继提出了鼓泡EMMS稳态模型[45]和并/逆流EMMS稳态模型[68-69]。在此基础上,Liu 等[69-70]建立了基于EMMS的全流域统一建模方法并绘制了操作相图。Tu等[71]进一步指出,当对多回路循环流化床系统进行全回路模拟时,必须恰当地考虑各子反应器模块的边界条件及单元操作之间的强耦合作用。EMMS操作相图为循环流化床反应器内的流域识别和量化表征提供了可行途径。通过考虑各模块之间的压降平衡和全床物料守恒关系,所谓的EMMS 全回路建模方法可以实现对该类反应器整体稳态动力学的准实时预测[70,72]。 本文将重点介绍和总结本课题组在气固系统介尺度建模和EMMS模型扩展方面的工作。首先介绍基于团聚物或气泡的EMMS曳力模型的改进和发展;第二部分论述介尺度结构时空动态演化行为对本构关系的影响,以及群平衡模型在气固流态化系统中的应用;第三部分介绍基于EMMS 的反应器宏尺度建模方法,包括模型的扩展、相图绘制和全回路建模等;最后是对未来工作的展望。 如图1 所示,EMMS 模型将非均匀气固系统分解为颗粒富集的密相和气体富集的稀相,两者之间通过相界面相互作用[1]。假设两相内的气固相互作用可以用均匀模型描述,则特定操作条件系统状态可以用8个参数X={Upf,Uf,εf,Upc,Uc,εc,f,dcl}来定义。通过对稀密两相分别建立质量和动量守恒方程,再加上两者之间的压降平衡方程及团聚物直径关联式,总共6 个守恒方程得以建立。Li 等[1,27]认为在气固流态化系统存在两种控制机制:当流体控制时,Wst=min;颗粒控制时,ε=min。两者的竞争协调关系构成了系统的稳定性条件,即 图1 EMMS模型的物理图谱和表达式[65]Fig.1 Physical concept and formulation of the EMMS model[65] 以上稳定性条件和守恒方程共同构成EMMS模型。在给定的宏尺度操作条件下时,X可以通过数值方法求解。然而,由于EMMS 模型最初用于描述流化床系统的整体流动结构,将其拓展到计算网格求解有效曳力时至少需要解决和考虑以下问题:(1)局部结构远离平衡态,模型方程如何考虑颗粒加速度的影响;(2)原稳定性条件在拓展到其他流域时应该如何改进;(3)曳力关联式的形式及其计算方法。 EMMS模型基于能量平衡假设建立了团聚物方程,但该方程难以适用于低通量、高加速度和顺重力情形,这限制了模型在曳力计算中的应用。为了改进对颗粒团聚动力学的描述以提高EMMS曳力模型的普适性,Hu 等[30]通过量化团聚物和稀相颗粒之间的质量交换关系,提出了团聚物动态平衡方程,并以此替换原团聚物方程对EMMS 模型进行了改进。如图2(a)所示,通常情况下,流体计算网格中呈现稀密相共存的非均匀两相结构。在团聚物存续时间内,稀相和密相颗粒之间的质量交换可以认为由两个可逆的过程组成。如图2(b)所示,对于球形颗粒物,在迎风面,稀相颗粒和团聚物发生非弹性碰撞导致颗粒被聚团捕捉;而在背风面,团聚物表面颗粒在随机脉动作用下进入稀相。两者满足动态平衡时可得 图2 EMMS曳力模型中亚网格非均匀性(a)和稀密相质量传递过程(b)Fig.2 Sub-grid heterogeneity(a)and solids mass transfer between the dilute and dense phases(b)in the EMMS drag model 其中,w是常数,本研究取1/12。密相颗粒温度Θc的计算可参考文献[30]。根据图2(a)可以分别对稀相和密相建立守恒方程。连续性方程同原EMMS模型(图1)一致,但由于局部结构往往远离平衡态,颗粒的加速效应常不能忽略,稀密两相的力平衡方程应改写为 非均匀性因子定义为EMMS曳力系数和均匀曳力系数的比值,即 图3 改进EMMS曳力[(a),(c),(e),(g)]和均匀曳力[(b),(d),(f),(h)]对快速床提升管[(a)]、湍动床[(c)]、变径提升管[(e))及下行床[(g)]的预测结果[30,51,73]Fig.3 Snapshot of solids concentration in the fast fluidized riser[(a)],turbulent bed[(c)],tapered riser[(e)]and co-current downer[(g)]by using the improved EMMS drag model[(a),(c),(e),(g)]and the homogeneous drag model[(b),(d),(f),(h)][30,51,73] 传统的EMMS曳力计算依赖系统宏观操作参数(如Ug、Gs等),构建满足伽利略不变性的EMMS曳力模型可以避免当操作条件改变时必须重构Hd系数关联式的问题,并可以适应具有复杂几何结构的流化床反应器的曳力计算。建立满足伽利略不变性EMMS曳力模型的重要步骤是将方程中的绝对速度项转化为相对速度项。根据滑移速度的定义,式(2)可以重组为 借助相间压降平衡方程消去式(3)、式(4)中的Fi可得稀密相力平衡方程(k=c 代表密相;k=f 代表稀相) 为了获得满足伽利略不变性的稳定性条件的等价表达,Hu 等[54]分析了不同操作条件下EMMS 模型的解集,发现当气固物性不变时,密相空隙率可以近似表达为平均空隙率的函数。对于典型A类颗粒(dp=60 μm,ρp=1490 kg/m3)有 质量守恒方程(气相、固相和固含率)、模型基本假设(εf→εmax,af→0)及式(7)~式(9)共同构成满足伽利略不变性的EMMS 曳力模型。可见,相对原来的非线性优化求解,上述模型的求解复杂度大大下降,可以容易地构建Hd关于(ε,Re)的关联式或在模拟过程中直接对模型进行在线求解。图4(a)展示了采用该模型计算得到的非均匀因子,其随空隙率和Reynolds 数的变化符合物理规律[54]。图4(b)进一步比较了本模型、改进EMMS 模型和实验数据的对比。可见式(9)的简化并未降低模型的准确性,但模型的普适性有了很大提高。 图4 满足伽利略不变性的EMMS曳力模型[54]Fig.4 EMMS drag model following Galilean invariance[54] EMMS 曳力模型也被拓展到气固鼓泡流态化系统[43-44,46,49-50]。但由于经验性的气泡关联式往往基于特定的实验条件获得而难以被推广到其他情况,因而Liu 等[45]提出了采用改进稳定性条件来约束气泡尺寸的方法。 如图5 所示,气固鼓泡流态化系统可以分解为气泡相和乳化相,共采用9 个结构参数X={Ub,fb,εb,db,ab,Uge,Upe,εe,ape}来定义。但为了简化计算,一般假设气泡中不含颗粒,即εb=1.0。分别以颗粒和气泡为研究对象可以建立一系列连续性方程和力平衡方程。与上述基于团聚物的EMMS 模型不同,EMMS鼓泡模型一开始就考虑了颗粒和气泡的加速效应,且在稳定性条件的表达上也有很大的变化。这是因为气泡在长大过程中会因为相界面的正压力而产生能量耗散,因此在计算单位质量床层的悬浮输送能耗(Nst)时,除了曳力做功外,还应额外考虑气泡克服乳化相压力膨胀所做的体积功。系统的稳定性条件定义为相对悬浮输送能耗趋于最小,其具体形式见图5。改进后的稳定性条件中包含了气泡直径的影响,这为气泡直径的取值提供了自然约束,避免了经验关联式的引入。 图5 EMMS鼓泡曳力模型的物理图解和公式Fig.5 Physical diagram and formulation of the bubbling EMMS drag model 在鼓泡床中,非均匀性因子可以表达为 鼓泡EMMS 曳力的计算及与CFD 耦合的方式同1.1 节类似,此处不再赘述。如图6 所示,相对均匀曳力模型,EMMS 鼓泡曳力模型可以更好地预测反应器的非均匀结构,与实验数据呈现更好的一致性,这也说明了模型的合理性。关于模型方程的推导和实验验证的详细信息可以见文献[45]。 图6 采用EMMS鼓泡曳力和均匀曳力对A类颗粒鼓泡床的模拟结果对比[45]Fig.6 Comparison between the bubbling EMMS model and homogeneous model in predicting the gas-solid bubbling beds of Geldart A particles[45] 在传统的EMMS 曳力模型中,所取团聚物直径可以认为是当前操作条件(Ug,Up,ε)下的最概然值或统计均值,而团聚物的动态特征及尺寸分布(CSD)信息未被考虑。为了定量描述团聚物的时空动态分布及其对网格内曳力的影响,Hu 等[62]提出了基于团聚物的群平衡方程,并进一步建立了CFD、PBM及EMMS模型的耦合计算框架。 以团聚物直径(L)为内坐标,团聚物尺寸演化的群平衡方程可以表达为 式中,n(L,x,t)表示尺寸为L的团聚物在t时刻和x位置的数密度;B(L,x,t)和D(L,x,t)分别表示由于聚并和破碎效应导致的团聚物生成项和消亡项,一般表达为 由于流化床中颗粒湍流及团聚物聚并、破碎的机制尚不明确,因此初步研究主要聚焦于团聚物和稀相颗粒的碰撞和离析等连续演化过程。通过分析单位时间颗粒和团聚物的非弹性碰撞及稀相流体对聚团表面颗粒的侵蚀效应,Hu 等[62]建立了团聚物的连续生长方程,代入PBM可得 式(14)理论上更适用于床层较稀的工况。通过离散法或矩方法可以对上述方程进行求解,进而可以获得团聚物的数密度函数及网格内的平均直径分布。 前述信息可以用来封闭EMMS曳力模型中的团聚物直径项。图7 展示了CFD-PBM-EMMS 的耦合计算框架:首先利用CFD 模型计算得到的t时刻所有网格内的相速度、空隙率、湍流特征量并传递给PBM;求解PBM 可以得到t时刻网格内团聚物的尺寸分布(CSD);将以上CFD 和PBM 的求解信息传递给EMMS 曳力模型,进而获得粗网格的有效曳力系数,并提高CFD的计算精度。 图7 CFD、PBM和EMMS模型的耦合Fig.7 Integration of the CFD,PBM and EMMS models 耦合模型可以有效避免实际团聚物直径和传统EMMS预测值不一致的现象,具有更好的自洽性。更重要的是,该算法可以直接计算反应器内不同位置处团聚物的尺寸分布随时间的演化规律,这对反应器的设计和优化无疑具有重要的意义。图8(a)展示了基于PBM 修正的EMMS 曳力校正系数,可见该模型合理地预测了团聚物尺寸这一关键参数对Hd的影响。通过图8(b)可见,相对均匀曳力和传统EMMS 曳力,本模型可以更好地预测流化床内的非均匀分布。另外,群平衡模型还可以对团聚物的尺寸分布进行直接预测,如图8(c)所示。 图8 CFD-PBM-EMMS耦合模型在快速流态化中的应用[62]Fig.8 Implement of the CFD-PBM-EMMS model in the fast fluidized beds[62] 在气固鼓泡流态化中,气泡自分布板上部生成之后,往往经历复杂的聚并、破碎等动态演化过程[74-75]。很多研究采用实验和经验建模的方式对气泡的尺寸分布进行研究和建模,不仅难以适应各种复杂操作条件,也无法对气泡的动态时空分布进行准确计算。采用这些经验方程进行封闭也在很大程度上影响了曳力模型的准确性和合理性。 根据Hu等[63]的研究,气泡的聚并主要由大小气泡的上升速度差异和气泡的尾流加速引起的,因此根据两者的物理过程可分别建立其聚并核函数。大小为di和dj的两个气泡的聚并频率可以表达为 式中,λr和λw分别表示由于气泡追赶和尾流效应导致的聚并效率[63];θw表示尾流的平均张角;urel,w表示由于尾流诱导产生的碰撞速度,实验发现该附加速度和碰撞发生时的气泡上升速度大小相当。气泡的破碎机制则更加复杂,一般认为是顶部颗粒快速下落导致的气泡切割和分裂。通过对实验数据回归发现气泡的破碎频率和其直径的2.9 次幂成正比。因此,直径为di的气泡破碎频率可以通过式(16)关联获得 而破裂导致的子气泡概率分布函数则采用实验统计的拟合函数。体积为Vʹ的气泡破碎生成的子气泡近似满足以下高斯分布 将式(15)~式(17)代入式(11)~式(13)可以得到气泡的群平衡方程。采用和图7一致的建模思路建立鼓泡床的CFD-PBM-EMMS 模型。如图9(a)所示,借助PBM 封闭的鼓泡EMMS 模型合理地考虑了气泡直径对非均匀曳力的影响。在气泡直径趋于0时,曳力自然趋于均匀曳力。图9(b)是模型预测结果和实验的对比,可见该模型可以较好地预测气泡尺寸沿床层高度的分布规律。 图9 CFD-PBM-EMMS耦合模型在鼓泡流态化中的应用[63]Fig.9 Implementation of the CFD-PBM-EMMS model in the bubbling fluidized beds[63] 研究表明气固流态化和物质相变具有相似的多状态特征,随操作条件改变呈现不同的非均匀分布和连续的流域转变[76-78]。量化流化床的宏尺度稳态动力学不仅可以快速了解反应器的操作状况,亦可以作为初始分布加速工业级反应的数值模拟过程。Hu 等[67]发现在提升管底部团聚物具有强烈的碰撞、聚并作用,而在顶部团聚物组织松散,稀密相差异很小。在此基础上,通过引入颗粒加速度建立了EMMS 轴向模型,首次实现了对提升管反应器中轴向S 形非均匀分布的EMMS 预测[67]。根据轴向模型获得各截面处的平均空隙率和气固速度信息,Hu等[30]进一步改进和完善了径向EMMS 模型,并通过函数逼近的方法实现了对提升管中径向环核结构的数学预测。 图10 展示了径向EMMS 模型的物理框架。自上而下,在截面尺度,各物理量必须满足截面稳定性条件和边界约束的守恒方程;在单元介尺度,各径向微元体内参数服从于稳定性条件和质量动量守恒方程;而在颗粒微尺度,气固相互作用在稀密两相内呈现均匀结构,可以用均匀曳力计算。与提升管反应器类似,气固下行床中也存在颗粒团聚现象。因此,上述轴径向建模思路也被应用到气固并/逆流下行床的计算。将气固并/逆流下行床进行结构分解,分别建立各相的质量和动量守恒方程以及不同发展阶段的稳定性条件,最终可建立EMMS 并/逆流下行床数学模型[68-69]。至于鼓泡流态化系统,气泡的形成和演化代替了提升管中颗粒团聚物的聚并和破碎而成为系统的主要非均匀结构特征。假设乳化相的颗粒加速度为0,则图5所示方程可以直接用于鼓泡床稳态动力学的求解。模型无须经验气泡直径的辅助就可对鼓泡床动力学进行预测[45]。 更多研究细节和实验验证可参考文献[30,45,67-70]。 图10 提升管径向非均匀分布的EMMS稳态建模[64-65]Fig.10 Modelling of radial hydrodynamics of risers by using the EMMS model[64-65] EMMS模型在二维空间以及不同流域的扩展使广义流态化相图的绘制成为可能。根据Kwauk 广义流态化相图的绘制思路[79],遍历不同操作范围的气体速度(=Ug/Ut)和颗粒速度(=Up/Ut),判断其所处流域,进而采用相应的EMMS 模型或扩展模型计算床层的平均空隙率,最终可得如图11所示的操作相图。值得说明的是,该相图给出了典型流域转变时的特征速度曲线,如噎塞曲线、液泛曲线和湍动流态化速度的参考值。噎塞的预测作为EMMS模型的重要特征已经被广泛讨论,这里不再赘述。而湍动流域的确定一直存在广泛争议,不同研究者对湍动气速的确定标准持有不同的观点。本研究根据基于团聚物的原始EMMS模型和基于气泡的鼓泡EMMS 模型联立求解,所获得的二者的交叉点被认为是连续相从密相转变为稀相的相转变点,并将其所对应的流体速度定义为湍动流态化速度,如图中黑色虚线Uc所示。而液泛作为另外一个重要的流域转折特征,一般发生在当逆流床的气速或颗粒通量过大时,颗粒被气流带出从而中断系统操作的状态。通过考察EMMS 逆流下行床模型解的特点,本研究将空隙率对气速二阶导的最大值点设为液泛发生速度,而EMMS 无解点设为液泛终止速度[65],并通过和实验对比验证了这种定义的合理性。 图11 Geldart B类颗粒的EMMS广义流态化相图[69]Fig.11 EMMS-based generalized fluidization phase diagrams for Geldart B particles[69] 基于以上各扩展模型和操作相图,本课题组进一步完善了基于EMMS方法的循环流化床全回路稳态计算模型[70,72]。 图12(a)展示了循环流化床全回路建模的基本流程:(1)首先根据系统的边界和接口情况将其划分为不同的循环通路和相应的子反应器组合;(2)遍历各循环通路内的颗粒循环量等参数,并根据所处的气固流速选择合适的计算模型,如果操作处于广义流态化状态,则选取EMMS 扩展模型计算或通过相图查阅该单元内的动力学参数,其他单元模块如旋风、出口管等则使用经验关联式求解;(3)根据系统的压降平衡和物料平衡迭代计算直到收敛。图12(b)是一套多产异构烷烃的催化裂化过程冷态实验装置。图12(c)是对该反应器进行全回路计算的结果,可见模型可以合理预测反应器内流动参数的宏观分布。 图12 基于EMMS的循环流化床统一建模[72]Fig.12 EMMS-based general method for global hydrodynamic calculation of typical CFB systems[72] 为实现流化床反应器整体稳态动力学的快速计算,EMMS 全回路建模方法还被封装成软件Virtual Fluidization(2015SRBJ0279)。软件采用模块化设计,可以根据实际的工业装置自定义搭建、更改和优化反应器设计。软件系统通过调用全循环计算代码可以在几秒到几分钟之内完成稳态动力学的计算和显示。如图13所示,系统合理预测了不同操作条件下反应器内的各模块的颗粒浓度非均匀分布。通过导出整体分布数据作为后续CFD 计算的初场,可以提高CFD模拟的效率和速度。 图13 采用Virtual Fluidization软件对循环流化床系统的稳态动力学进行模拟[72]Fig.13 Simulation of steady-state hydrodynamics in a CFB system by using the software Virtual Fluidization[72] 能量最小多尺度方法为多相非均匀系统的数学建模提供了一种可行的理论框架。采用该方法能够计算局部介尺度结构对相间曳力等本构关系的影响。但经典EMMS曳力模型所采用的团聚物方程在极端操作条件下存在求解不适定的问题,而通过量化稀密相间固相质量传递可以建立更通用的颗粒团聚动态平衡方程,基于该方程的改进EMMS曳力可以更合理地计算快速床、湍动床和下行床的非均匀分布。通过改进EMMS鼓泡模型的稳定性条件,无需气泡经验关联式辅助即可实现对亚网格鼓泡曳力的直接预测。 通过考虑气泡和团聚物的聚并、破碎演化动力学,群平衡模型实现了对该类介尺度结构时空动态演化行为的定量表征。通过群平衡方程在线封闭EMMS 模型中的气泡/团聚物直径项可以更准确地计算局部结构曳力系数,从而提高CFD 模拟的可靠性。 通过对EMMS 模型在轴径向二维空间、鼓泡床和下行床进行拓展,建立了适应不同操作模式和操作条件以及流域的反应器宏尺度稳态模型,并绘制基于EMMS 的气固广义流态化相图,反映不同操作模式下床层空隙率、噎塞和液泛气速等特征变量随操作条件的变化。原EMMS及其拓展模型被应用到循环流化床系统的全回路建模,实现了对复杂回路气固系统的准实时稳态动力学计算。 未来的工作可聚焦介尺度结构的动态演化机制,通过实验和模拟等手段探索局部非均匀结构的时间演化特征并量化这种动态结构对曳力、固相应力及湍流耗散等本构关系的影响。另外,复杂反应器的快速准确建模对工业应用具有重要意义,如何结合介尺度模型、高效数值模拟方法以及神经网络方法建立完善的多尺度计算模式也是值得努力的方向。 符 号 说 明 a——加速度,m/s2 a(L,λ)——直径为L和λ的单体聚并频率,m3/s B——生成源项,m-4/s CD——单颗粒曳力系数 D——消亡源项,m-4/s dcl——团聚物直径,m dp——颗粒直径,m Fc——单位体积密相颗粒所受曳力,kg/(m2·s2) Ff——单位体积稀相颗粒所受曳力,kg/(m2·s2) Fi——单位体积床层团聚物所受稀相曳力,kg/(m2·s2) f——密相体积分数 Gs——颗粒循环率,kg/(m2·s) g——重力加速度,m/s2 g(λ)——破碎频率,s-1 Hd——非均匀性因子 L——内基变量,此处为单体直径,m Nst——气体流过单位质量颗粒床层的悬浮输送能耗,J/(kg·s) NT——气体流过单位质量颗粒床层的总能耗,J/(kg·s) n——基于长度的数密度函数,m-4 p——破碎元 Re——Reynolds数 U——表观速度,m/s Umf——起始流态化速度,m/s Ut——颗粒终端速度,m/s u,u——速度,m/s Wst——气体流过单位体积床层的悬浮输送能耗,J/(m3·s) βE,βhomo——分别为微元体的有效曳力系数和均匀曳力系数,kg/(m3·s) β(L|λ)——碎片分布函数 ε——体积分数 εmax——团聚物存在的最大空隙率 λr,λw——气泡追赶和尾流导致的碰撞效率 ρ——密度,kg/m3 Θc——密相颗粒温度,m2/s2 θw——尾流的平均张角 ω——概率因子 下角标 b——气泡 c——密相 e——乳化相 f——稀相 g——气体 p——颗粒 s——滑移1 EMMS曳力模型
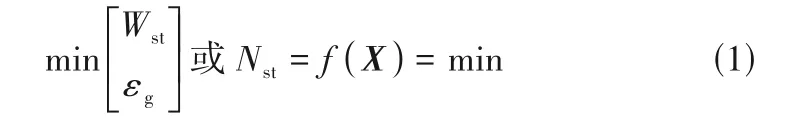
1.1 改进的基于团聚物的EMMS曳力
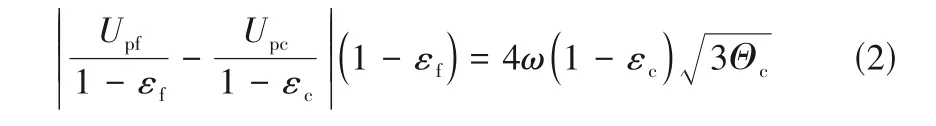

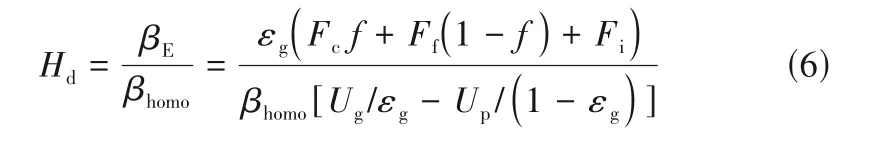

1.2 具有伽利略不变性的EMMS曳力

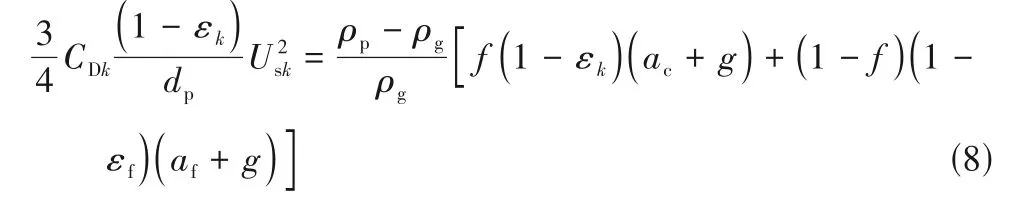
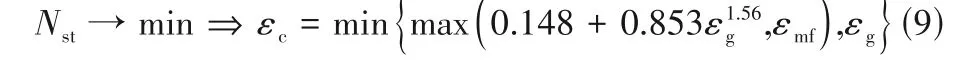
1.3 改进的基于气泡的EMMS曳力

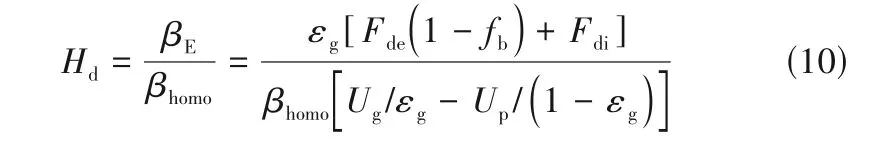
2 介尺度结构时空动态演化的群平衡建模
2.1 基于团聚物动态演化的群平衡建模


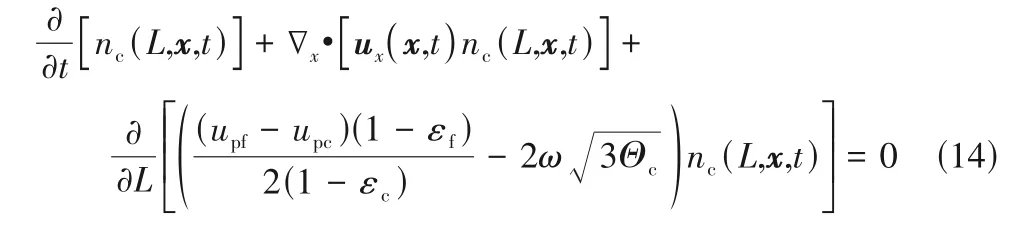

2.2 基于气泡动态演化的群平衡建模



3 基于EMMS的全流域操作相图和全回路稳态建模
3.1 稳态EMMS模型的扩展和相图绘制
3.2 循环流化床全回路稳态建模及软件开发

4 总结与展望
