基于微量热法对多孔碳与双氧水相互作用过程的传质阻力分析

2022-07-06曹健叶南南蒋管聪覃瑶王士博朱家华陆小华

化工学报 2022年6期

曹健，叶南南，蒋管聪，覃瑶，王士博，朱家华，陆小华

（南京工业大学材料化学工程国家重点实验室，江苏南京 211816）

引言

近年来，各种新型高效多功能催化剂如分子筛[1-2]、贵金属催化剂[3]等，能够大幅提高反应转化率，反应工艺条件却更缓和，很大程度上推动了化学工业的发展[4-5]。其中，多孔材料作为催化剂具有大比表面积，反应性能优异，但反应物在纳米受限孔道下的物性、状态变化等传递行为对催化的作用与反应等量齐观[6-11]，不容忽视，不仅要考虑该尺度下分子之间发生反应的可能性与条件，还要研究流体的传递及其对反应过程与产物的影响。如何阐明纳微界面传递与反应竞争博弈的介尺度机制迫在眉睫[12]。

在面向现制即用绿色过程的双氧水(H2O2)直接合成过程的课题组前期研究中，发现H2和O2直接合成的H2O2是该多相反应的中间产物[13]，将生成的H2O2及时从催化剂表面脱附是提高产率的重要途径；掺碳可有效降低H2O2与TiO2表面的相互作用强度以强化脱附[14]。并从反应热和熔化焓的角度剖析了直接法合成H2O2负载型纳米金属催化剂的传递-反应机制[15]。作为典型的介尺度问题，目前仍存在界面传递机制内涵模糊且尚无普适性表达、界面传递和反应交织的复杂过程缺少定量描述等问题。因此，仅通过化工经典“三传一反”理论难以解释其复杂机制。

非平衡态热力学理论利用化学势梯度（通用推动力）为解耦界面扩散与反应过程提供了统一框架[16]。陆小华团队利用非平衡热力学线性化方法简化接近平衡态系统的界面传递模型[17-19]。基于离子选择性电极(ISEs)准确测定含钾化合物溶解结晶的传质通量[20]，剥离出钛酸钾制备过程中离子交换速率的受控因素并加以强化，实现其低成本、规模化的生产；基于热重分析(TGA)测定离子液体支撑膜吸收CO2传质通量[21-23]，揭示过程关键阻力是扩散层厚度。将此研究思想拓展至多相催化的扩散反应介尺度机制研究时，缺少准确通量测定方法，多孔结构等带来的纳微尺度复杂界面结构尚无通用手段能够进行描述。

因此，本文设计多孔碳与双氧水(H2O2)相互作用的微量热实验，利用热效应求解H2O2的传质通量及化学位推动力，构建扩散-反应传质阻力模型。利用分子模拟获取介孔及微孔特征结构参数有效传质距离，结合比表面积测试，对扩散及反应的传质面积进行差异性描述，实现扩散与反应阻力的定量描述，从而获得体相及界面处浓度的动态时空变化，为多孔催化剂中扩散及反应过程的介尺度机制及调控研究提供助力。

1 实验设计及方法

1.1 实验设计

为研究H2O2在催化剂表面的反应及脱附过程，应用线性非平衡热力学方法需要准确测得H2O2的传质通量[24]。而界面处的脱附起始时间难以确定，缺少相关表征手段。脱附过程的传递能力强，则对应吸附过程的传递性能优异。故设计以H2O2吸附的传递过程等当在同样孔道结构下脱附的传递过程，通过溶液中H2O2的浓度变化即可获得传质通量。由于需要对传质过程的动力学数据进行大量处理，要求通量测定方法具有足够精度，ISEs 和TGA 均满足精度要求，但适用范围分别是离子浓度及液体质量的变化，在本研究中不再适用。

反应热是构建H2O2传质通量的媒介，并可通过高精度的微量热实验准确获取过程的热效应。H2O2经过孔道扩散后，在多孔材料表面发生反应或吸附相互作用会产生一定热效应，通过热效应可以获得H2O2的传质动力学数据。一定量的H2O2(可完全消耗) 与多孔材料相互作用过程中，单位时间下的热通量与相互作用总热量的比值反映的就是固定量H2O2在单位时间下的消耗量，从而获得H2O2传质通量随时间的变化曲线。

1.2 实验材料及方法

本实验所用试剂及材料见表1。其中，生物骨架碳BioMC、负载Pd 金属的碳材料1%（质量）Pd/BioMC和1%（质量）Pd/Cabot均在实验室制备。

表1 本实验所用试剂及材料Table1 Reagents and materials used in this experiment

微量热实验采用美国TA Instruments 公司TAM Air 热导式恒温滴定量热仪，其热流检测限为±4 μW，控制温度的波动为±0.01℃。测定氯化钾在纯水中的溶解热，与其标准热力学数据[25]相对误差为0.9%，可见实验具有足够精确性。

测量过程使用平行的双腔测量通道，即测量通道和参考通道。在测量通道中，使用灵敏度为10-5g、不确定度为± 6×10-5g 的数字分析天平(型号：Sartorius SECURA225D-1CN)称量30 mg碳材料加入20 ml安瓿瓶中，同时使用5 ml的移液枪向安瓿瓶中加入2 ml 纯水，使碳材料充分混合分散。利用安瓿顶部带自动搅拌的Hamilton 注射器取1%（质量）的H2O2水溶液2 ml。在参比通道中，Hamilton 注射器中的H2O2水溶液换为等量纯水，用于消除外部温度变化引起的测量误差。测试过程中将测量通道及参考通道Hamilton 注射器内溶液注入安瓿瓶内，H2O2与多孔碳相互作用的热信号可被自动记录。当系统达到平衡时，即热流随时间保持恒定时，热量由进样后基线上观察到的峰面积确定。

比表面积及孔隙结构分布采用Micromeritics Tristar Ⅱ3020 分析仪（Micromeritics，美国）测定，使用N2等温线吸附法测试。测试前样品在250℃下真空脱气6 h。基于测量的吸附/解吸等温线，使用Brunauer-Emmett-Teller (BET) 方法计算碳材料的比表面积、微孔和介孔的孔容。

2 模型构建

2.1 H2O2传质通量

在多孔碳与H2O2之间发生催化反应或吸附过程时，H2O2的传质通量为：

式中，JH2O2为H2O2的传质通量，mg/s；dmH2O2,t为体相溶液中H2O2消耗量，mg；t为时间，s。通过微量热实验的热信号求解传质通量动力学数据时，单位时间的热效应及传质通量分别与总热量及总传质量符合定量比例关系：

式中，mH2O2为体相水溶液中H2O2的总量，mg；q为单位时间时的热效应，J/s；T0和Tf分别代表多孔碳与H2O2相互作用的起始和终止时间，s。

2.2 基于化学势的传质阻力

基于线性非平衡热力学理论将化学位梯度(ΔμH2O2)作为推动力[18]，则有：

式中，KA为基于化学势的H2O2表观总传质系数，mg/s；ΔμH2O2为化学位梯度；μH2O2,e及μH2O2,t分别代表H2O2在平衡及t时刻的化学位；R为气体常数；T为温度，K。值得一提的是，基于化学势推导出的KA不是简单的模型回归参数，具有一定物理意义。

在H2O2浓度较低时，忽略溶液的非理想性[26]，此时H2O2的活度等于其浓度。因此H2O2在溶液中的化学位可以表示为：

其中，xH2O2为H2O2在体相溶液中的浓度，结合式(1)～式(4)，可以给出传质阻力1/KA的表达式：

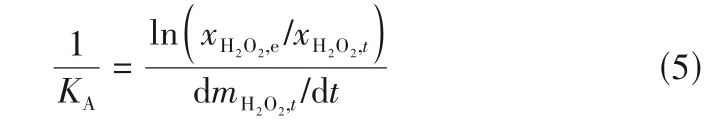
2.3 扩散-反应模型

多孔碳与H2O2的相互作用可以视为扩散与反应两个过程的串联[19]。如图1 所示，H2O2分子自多孔碳孔口处，首先经过孔道内的分子扩散，到达活性位点处发生反应（吸附可视为表面的“拟化学反应”过程）[26]。若以化学势梯度为推动力，则该过程扩散速率和表面反应过程速率分别描述为:

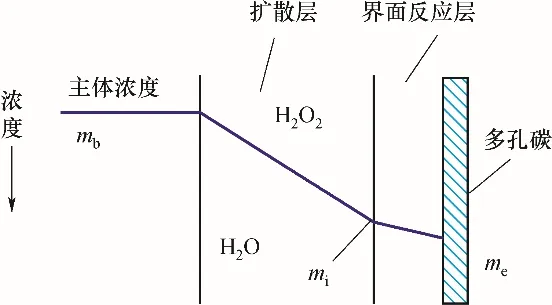
图1 线性非平衡热力学传质模型Fig.1 Linear non-equilibrium thermodynamic mass transfer model

式中，kd和ks分别代表扩散速率系数及相互作用(反应)速率系数，mg/(m2·s)；μe、μi及μb分别为固相、固液界面和主体相的化学位。与离子液体膜吸收/解析CO2过程[23]扩散与“拟反应”面积等当不同的是，多孔碳扩散与反应过程的速率不能单因素化于比表面积，扩散通量还取决于孔径与孔个数。如图2 所示，提出将扩散与反应面积进行差异性描述，A及ap分别代表扩散截面积及比表面积。因此过程传质总阻力可以分解为扩散层阻力与反应层阻力之和：

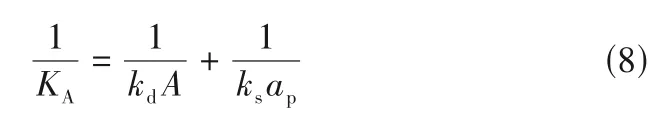
扩散层阻力可以进一步分解为介孔扩散阻力与微孔扩散阻力。如图2所示，孔道结构错综复杂，既有微孔呈现介孔分叉的等级孔形式[27-28]，视为介孔与微孔阻力的串联；亦存在微孔与介孔的竞争扩散，可以视为介孔与微孔阻力的并联。引入结构参数η，代表等级孔形式的微孔占所有微孔的比例，则1-η代表与介孔竞争扩散的微孔占所有微孔的比例。将介孔与微孔理想化为圆柱孔[29]，扩散层阻力可以表示为：

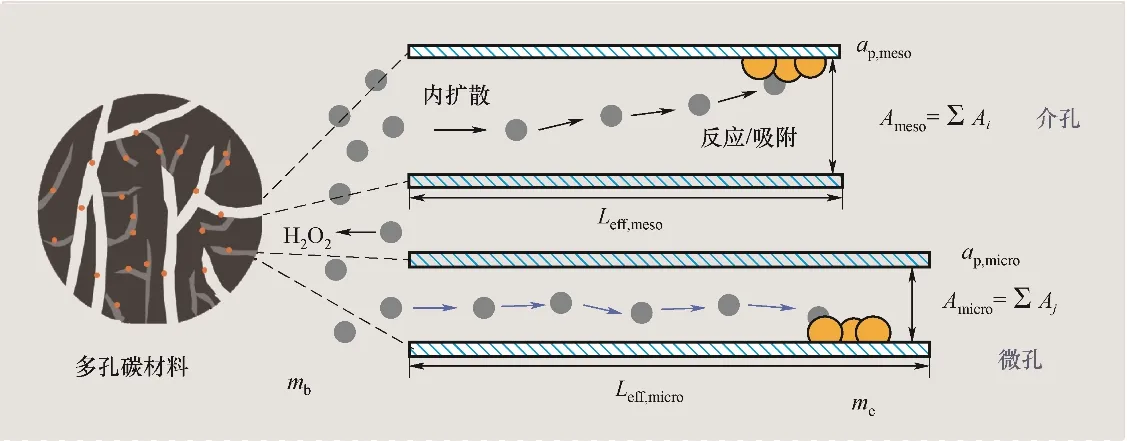
图2 多孔碳反应/吸附H2O2过程示意图Fig.2 Schematic diagram of reaction or adsorption between porous carbon and H2O2

其中，Ai代表一个孔径为2ri介孔的扩散截面积；Aj代表一个孔径为2rj微孔的扩散截面积。式(9)代表了每个孔道对扩散层阻力的影响，但该方程难以求解，故将孔径分布以平均孔径代替。

ap可以通过BET 实验测定，而扩散截面积无法通过实验直接测定。借鉴课题组关于多孔碳材料中的甲烷传质研究[30]，利用有效传质距离Leff描述分子在孔道内的平均扩散长度，Leff可以通过分子模拟手段定性获取，主要考虑孔道结构与流体相互作用影响下对物性、状态的改变，体现分子在不同孔径孔道内的扩散难易程度。基于Leff，扩散截面积可以通过实验可测定的孔容Vg获得：

式中，m为多孔碳的质量，g；介孔与微孔的有效传质距离以平均孔径计，分别为Leff,meso和Leff,micro。为便于计算，可以定义kd,meso和kd,micro为考虑Leff后下的碳孔扩散速率系数：

结合式(8)～式(12)，可以给出多孔碳的传质总阻力表达式：

3 结果及讨论

3.1 实验结果

对四种多孔碳材料分别进行与H2O2相互作用的量热实验，采集到的热信号如图3(a)所示。图3（a）反映了不同时间下的瞬时热量变化。将图3(a)所示四条曲线以时间积分，可以获得总热量随时间的变化,如图3(b)所示。可以发现，四种多孔碳材料与H2O2相互作用的总热量变化差异较小。然而，图3(a)中1% Pd/BioMC 与H2O2相互作用的热信号呈现与其他三种碳材料极其显著的差异。可以定量描述从开始产生热效应到放热量趋于平衡的时间，1% Pd/BioMC 与H2O2相互作用的平衡时间约为30 min，而BioMC、1% Pd/Cabot、Cabot 分别约为160、220、240 min。将热效应的速率等当H2O2在不同多孔碳内传质通量，由实验室自制的1% Pd/BioMC 较商业碳Cabot的传质通量能够提高高达7倍。另外，相互作用的总热量包含吸附放热过程及H2O2分解反应的吸热，由图3(b)可以看出BioMC 和Cabot 担载1% Pd 对平衡态总放热量的影响接近，可代表反应活化能之差。

图3 四种多孔碳材料与H2O2相互作用的微量热实验结果Fig.3 Microthermal experiment results of interaction between four porous carbon materials and H2O2

由表2 多孔碳材料的BET 表征结果可知，实验室自制的BioMC 较商业碳Cabot 具有更大的孔容，主要体现在介孔孔容的大幅提高。负载1%Pd可少量提高材料的比表面积及孔容，这是因为酸性前体溶液在浸渍过程中可酸洗去除部分活性炭活化过程中产生的灰分。从四种活性炭与H2O2相互作用的平衡时间来看，负载Pd金属或高介孔孔容均能一定程度上强化传质通量，可以认为两种途径主要提高了图1中界面反应层与扩散层的传质速率。但经过单一方法强化的BioMC 和1% Pd/Cabot 并未出现数量级的传质通量强化。可见比表面积及孔容的提升并非关键优化因素，1% Pd/BioMC 反应层与扩散层的传质强化不是简单的叠加。

表2 多孔碳材料的BET表征结果Table 2 The BET characterization of porous carbon materials

3.2 阻力解耦

如式(5)所示，为求解非平衡热力学的传质阻力1/KA需要获取体相浓度、平衡浓度和传质通量。

根据式(2)可以通过微量热实验获得H2O2与四种多孔碳材料相互作用过程的传质通量，如图4 所示，进而可以获得体相浓度及平衡浓度随时间的变化。以ln(xH2O2,exH2O2,t)为x轴，dmH2O2,tdt为y轴绘制如图5 所示四种多孔碳材料不同时刻下的数据点，可以看出均呈现非常好的线性关系。对其进行线性拟合，所得线性关系的斜率为多孔碳材料与H2O2相互作用的总传质系数KA；斜率的倒数即为总传质阻力。

图4 H2O2的传质通量Fig.4 Mass transfer flux of H2O2

图5 四种多孔碳材料的总传质阻力Fig.5 Total mass transfer resistance of four porous carbon materials

通过分子模拟手段可以获得不同碳孔下H2O2与H2O 的扩散通量比[31]，发现介孔结构下，H2O2更易扩散至相互作用位点。Leff,meso和Leff,micro虽无法定量给出，但能基于分子模拟结果限定两者的比例关系：

以图3(b)所示平衡状态下的总放热量差异作为基于Arrhenius 方程反应活化能之差，可以通过微量热实验求解得到担载1%Pd对反应速率系数的增强关系：

其中，下角标pd 和null 分别代表担载和不担载Pd 元素多孔碳的反应速率系数。考虑到η的复杂性，本文将η理想化处理，BioMC 较好地利用了生物骨架结构，微孔与介孔主要呈现并联组合，η取0[32]；而Cabot 主要遵从等级孔造孔机理，微孔与介孔主要呈现串联组合，η取1。基于式(12)，结合式(14)、式(15)，可以任选两种多孔碳材料的总传质阻力建立方程组，求解kd,meso和ks,pd，kd,micro和ks,null根据比例系数求解获得。以1%Pd/BioMC 和1%Pd/Cabot求解，结果如表3所示，用于反求BioMC 和Cabot的总传质阻力，误差分别为4.5%和1.4%，说明该阻力求解方法具有一定可靠性。

表3 传质系数求解结果Table 3 Results of mass transfer coefficients

表4 展示了四种多孔碳的阻力分布，1% Pd/Cabot 的传质速率并未出现数量级变化的原因是其扩散阻力成为关键速率控制因素。BioMC及1%Pd/BioMC 由于其丰富的介孔结构，具有足够的传递通量，因此扩散阻力主要受介孔截面积影响；而Cabot及1%Pd/Cabot的介孔相对较少，扩散阻力的关键控制因素为微孔阻力，分别呈现并联及串联的阻力加和形式。1% Pd/BioMC 之所以具有超常传递性能，关键在于扩散阻力与反应阻力的匹配。

表4 四种多孔碳的传质阻力分布Table 4 Mass transfer resistance distribution of four porous carbons

3.3 介尺度机制

基于表4 所示传质阻力分布，可以求解图1 所示界面处浓度mi的时空变化，如图6 所示，以mi处H2O2的变化为研究体系，H2O2从体相扩散至界面的速率如黑色曲线所示，为正数，代表输入；界面反应层所消耗界面处H2O2的速率如红色曲线所示，为负数，代表输出。两者相加和即为蓝色曲线，反映界面处H2O2的动态变化。

图6很好地反映出传质通量受到传质阻力及推动力的综合影响。四种多孔碳材料界面处的扩散速率均呈现下降趋势，反应速率皆呈现先增强再下降趋势。这是因为传质阻力代表该材料的固有属性，为一定值，速率随着推动力的改变而变化。对扩散速率而言，体相H2O2不断消耗，推动力逐渐降低至0；对反应速率而言，由于扩散至界面需要一定时间，因此前期随着扩散量增大速率加快，到达一定极值后，扩散量降低，导致反应速率的降低。

从界面处H2O2的动态变化可以直观看出多孔碳材料与H2O2相互作用中介尺度机制A（扩散主导）和机制B（反应主导）的竞争与协调，蓝色曲线为正则代表机制A 占主导，为负则代表机制B 占主导。从反应阻力来看，1% Pd/Cabot 应该具有和1% Pd/BioMC 相接近的反应速率，但图6(b)所呈现的反应速率较图6(a)中的低几乎一个数量级，是由于扩散量不足以满足反应需求导致反应过程的推动力不足；图6(c)所示BioMC 虽然具有高的扩散能力，但扩散至界面的H2O2由于反应速率过慢而堆积，使得扩散过程的推动力迅速降低；由于相接近的扩散与反应速率，Cabot 中界面处H2O2的浓度变化呈现振荡，体现介尺度机制的竞争。此外，能够明确定量H2O2在复杂多孔材料中扩散及反应的相互作用机制，通过推动力实现两者的反馈与协调，定量揭示了研究中的两种传质强化并非简单叠加的关键原因，有望为揭示更复杂纳微界面传递与反应竞争博弈的介尺度机制提供理论依据。

图6 界面处H2O2浓度的时空变化Fig.6 Temporal and spatial variation of H2O2 concentration at the interface

4 结论

本文利用微量热实验测定1%（质量）H2O2与四种多孔碳相互作用的热效应，准确获得H2O2的传质通量及化学位梯度，基于非平衡热力学线性化方法解耦过程的扩散及反应阻力，揭示了多孔碳材料的界面传递结构，实现了扩散和反应交织的复杂介尺度问题的定量描述，得到结论如下。

（1）通过微量热实验、分子模拟及BET 孔结构信息可以求解揭示多孔材料扩散-反应的关键参数kd,meso和ks,pd，实现线性非平衡热力学的定量阻力分析，在本研究中该阻力分析方法误差仅为4.5%。

（2）实验室自制的1%Pd/BioMC 较商业碳Cabot的H2O2传质通量能够提高7 倍，是因为1% H2O2在多孔碳介孔中的扩散速率系数是在微孔中的2.45倍；在H2O2扩散过程中，生物骨架碳BioMC 的介孔与微孔的组合形式要明显优于商业碳的孔道组合形式；担载1% Pd 元素能够大幅增强反应速率系数达26.3倍。

（3）利用非平衡热力学方法所求解的扩散及反应阻力可以获得扩散-反应耦合的复杂介尺度过程的表界面浓度场动态分布，是揭示多相反应过程介尺度机制的重要定量描述方法，有望为过程的调控及优化提供理论依据。

符号说明

A——扩散截面积，m2

ap——比表面积，m2/g

J——传质通量，mg/s

KA——总传质系数，mg/s

k——速率系数，mg/(m2·s)

Leff——有效传质距离，m

m——质量，mg

R——气体常数，J/(mol·K)

r——孔道半径，m

T——温度，K