A hybrid genetic algorithm for the electric vehicle routing problem with time windows

Qixing Liu·Peng Xu·Yuhu Wu·Tielong Shen

Abstract Driven by the new legislation on greenhouse gas emissions，carriers began to use electric vehicles(EVs)for logistics transportation.This paper addresses an electric vehicle routing problem with time windows(EVRPTW).The electricity consumption of EVs is expressed by the battery state-of-charge(SoC).To make it more realistic，we take into account the terrain grades of roads，which affect the travel process of EVs.Within our work，the battery SoC dynamics of EVs are used to describe this situation.We aim to minimize the total electricity consumption while serving a set of customers.To tackle this problem，we formulate the problem as a mixed integer programming model.Furthermore，we develop a hybrid genetic algorithm(GA)that combines the 2-opt algorithm with GA.In simulation results，by the comparison of the simulated annealing(SA)algorithm and GA，the proposed approach indicates that it can provide better solutions in a short time.

Keywords Electric vehicles·Vehicle routing·Battery SoC·Hybrid genetic algorithm

1 Introduction

Over the years， the research of logistics and supply chains is increasing. Distribution tasks are usually represented as vehicle routing problems(VRPs).The objective of VRPs is to minimize the total transportation costs of serving a set of customers through some paths starting and ending at the depot.In recent years， many variants of VRP have been proposed to combine the constraints and conditions of the real-world[1].The capacitated VRP(CVRP)[2]and the VRP with time windows (VRPTW) [3]. The CVRP indicates that vehicles have a limited loading capacity， while the VRPTW means that the customers must be serviced within a specified period time. VRPs in different scenarios have also attracted much attention[4，5].To reduce the impact on the environment，an intuitive method is to use less polluting vehicles，such as EVs.The study of this paper belongs to this field.

EVs are one of the cleanest means of transportation，because they can be powered by sustainable and renewable energy sources [6]. Although in the early years， the high price of batteries and the short driving ranges once delayed the development of EVs.With the increasing battery life and rising fuel cost，EVs have gradually become one of the main research fields in the automotive industry. In some large companies， such as DHL， EVs have been used for urban transportation.

Most electric VRPs (EVRPs) only consider the energy consumption of paths and charging at the power stations with insufficient energy，without terrain factors.Within our work，we take into account the EVRPTW traveling on the terrain with grades. The EVs need to accelerate to overcome the grade resistance， and their energy consumption intends to increase.Furthermore，the EVs need to reduce the downhill speed such that they can partially recover the kinetic energy lostduringdeceleration，whichiscalledregenerativebraking.Our objective is to minimize the total energy consumption，while a fleet of EVs serves a set of customers.

The main contributions of this paper are:1)Based on the terrain with grades，we formulate the EVRPTW as a mixed integer programming model.Although the terrain modeling is not accurate enough， it does have a certain practical significance for the study of EVs driving on different slopes.2)A hybrid GA method is proposed to solve the EVRPTW.The addition of the 2-opt algorithm to the traditional GA can improve the equality of solutions.In addition to the contribution made in methodology，this paper mainly aims to propose a problem with practical motivation and design a comprehensive and customized solution to the problem. Extensive numerical studies on test instances demonstrate that the proposed method is very effective.

This paper is organized as follows.The literature review is in Sect.2.In Sect.3，problem formulation and some definitions are presented. In Sect. 4， we introduce our method for solving the EVRPTW.Simulation results on benchmark sets and the comparison experiments are shown in Sect. 5.The conclusions of this paper are given in Sect.6.

2 Literature review

Electric VRP(EVRP)is one of the research hotspots of VRP over the past few years.Linetal.[7]studied a general EVRP and considered the vehicle load effect on battery consumption.The objective was to minimize the total travel cost and energy cost as well as number of EVs.Samueletal.[8]investigated an EVRP with the energy consumption uncertainties.The objective was to determine the minimum cost delivery routes.Liaoetal.[9]also studied the EV shortest travel time path problem.

From the above discussion，the objective of EVRP is generally minimizing the total travel cost. There are still some variants of EVRP [10]. One of the most important variants is EVRP with time windows(EVRPTW).Guoetal.[11]addressed an EVRP with time windows.The authors considered the driving cost and punishment cost for time windows violation simultaneously.Schneideretal.[12]considered the constraints on vehicles and customer time windows.The aim was to minimize the number of employed vehicles and total travel distance on a flat terrain. Shaoetal. [13] considered the routes， charging plan and driving paths of EVRP. The objective function consists of vehicle fixed cost，travel cost and charging cost.The driving process of EVs in this problem considered the terrain without grades.Frogeretal.[14]studied the EVRP with capacitated charging stations，which was to minimize the total driving，charging and waiting time.

The solution methods of EVRPTW are usually heuristic approaches[15，16].To solve this proposed problem，we first make a comparison between GA and SA on the test instances using Solomon’s data sets. Based on the simulation results betweenGAandSA，wedevelopahybridGAwhichcombine the GA and 2-opt algorithm.Moreover，numerical simulation results show the better performance of our method.

To the authors’ knowledge， the topic of this paper， the EVRPTW with terrain grades， has not been studied previously by other researchers.

3 Problem formulation and definition

In the EVRPTW，let the depot be located at node 0，the set of customers is denoted byN1={1，...，r}，andNorepresents the other nodes along the paths.The set of all nodes is thenN={0}∪N1∪No.The set of all edges is denoted byE⊂N×Nsuch that an incomplete undirected graphG=(N，E)represents a road network of EVRPTW.Each edgeei j∈Eassociates with an actual distanceLi j.The demand of each customeriis denoted bydi，which needs to be served as soon as possible.Moreover，the time window of each customeriis denoted by [ei，li]， whereeiandlirepresent the earliest and latest time to start to service the customeri.The depot also has a time window[e0，l0]，indicating that EVs leave the depot no earlier thane0and return no later thanl0.

In our assumptions， the set of EVs is denoted byK={1，...，k0}. All EVs are assumed to be homogeneous， andQdenotes the loading capacity of each EV，qrepresents the electricity capacity of each EV. In particular， eachkth EV with battery SoC at nodeiis denoted by SoCki.The battery SoC consumed of unit distance is denoted byΔSoC.Therefore，the battery SoC consumed of edgeei jis represented asLi j·ΔSoC.

As is known to all， the terrain of the road network on a real-world situation is complicated. To be closer to reality，we consider each EV with dynamic of SoC traversing the edgeei j∈Eis as follows:

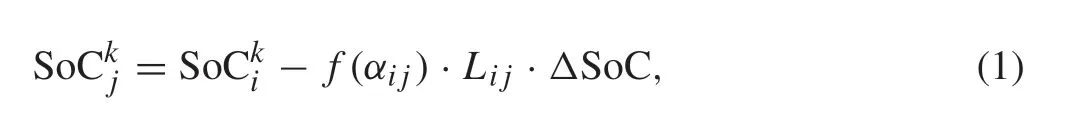
whereαi jis the average terrain grade from nodeito nodej.f(αi j)as a function of grade and electricity consumption from nodeito nodej.Let ¯αbe the critical value of average terrain grade.Iff(αi j)＞¯α，which indicates the EV is driving uphill;when thef(αi j)= ¯α，the EV travels on a flat terrain;iff(αi j)＜¯α，the EV is driving downhill.Accordingly，the velocity of EV from nodeito nodejis denoted byv(αi j).

The decision variablesxi jk(i／=j，ei j∈E) are binary variables that indicate whether thekth EV travels directly from nodeito nodej. If thekth EV travels directly from nodeito nodej，xi jk= 1， and otherwise is 0. We also let a continuous variableyikbe the arrival time at customeriof thekth EV that servesi.The mixed integer programming model for EVRPTW is as follows:

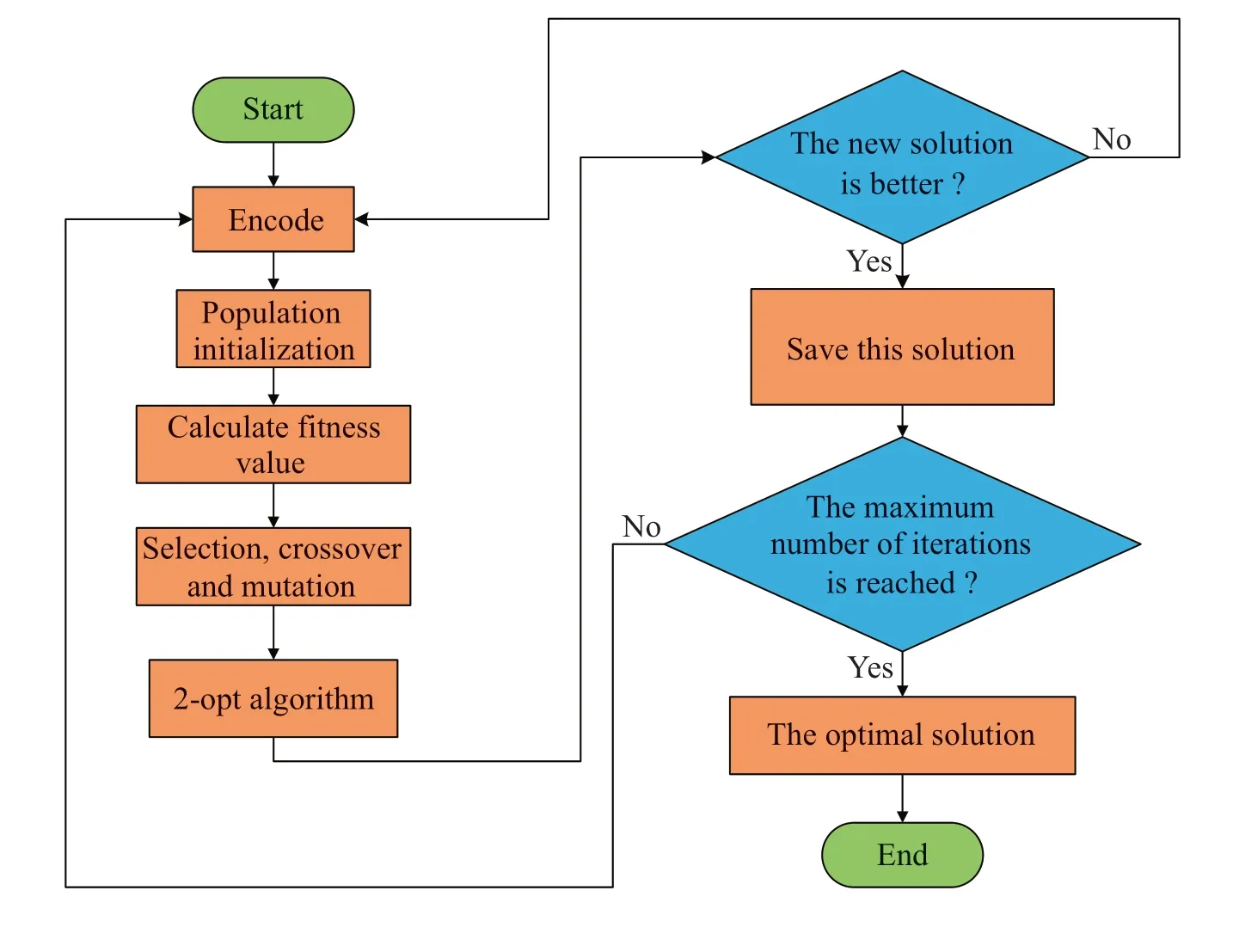
Fig.1 Flowchart of hybrid GA

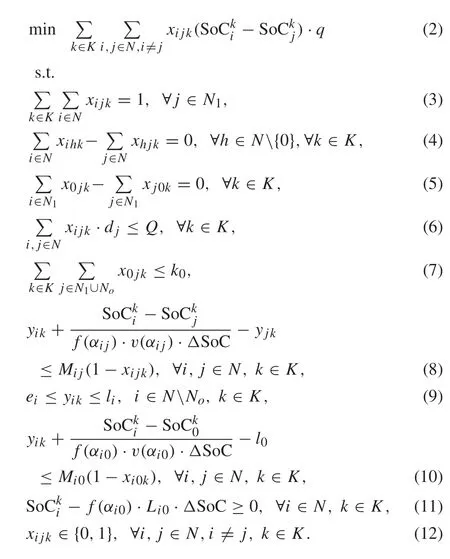
Equation(2)indicates the minimization of total electricity consumption of EVs. Constraints (3) require that each customer is assigned to exactly one EV.Constraints(4)state that to arrive at and leave each customer with the same EV.Constraints(5)ensure that EVs depart from the depot should eventually return to the depot.Constraints(6)guarantee that the vehicle capacity must be respected.Constraints(7)make sure that the number of served EVs should not exceed the maximum number of EVs used at the depot.

4 A hybrid GA solution method for the EVRPTW

As a solution method for EVRPTW，we propose a hybrid GA that consists of GA and 2-opt.GA was first proposed by Holland in 1975[17].It is an intelligent optimization algorithm according to the principle of“genetic inheritance”and“natural selection”in the process of biological evolution in nature.When GA is solving combinatorial optimization problem，the feasible solution of the problem forms chromosomes in some way， and some individuals are randomly selected to generate the initial population. Then， the objective function of combinatorial optimization problem is transformed into a fitness function in a certain way， and individuals are selected by calculating the fitness function value of individuals. Finally， individuals are finally selected， crossed，and mutated to produce individuals with higher fitness values. By continuous reproduction， the offsprings are more adaptable to the environment until the desired termination conditions appear. Thus， the optimal solution for the population is formed.

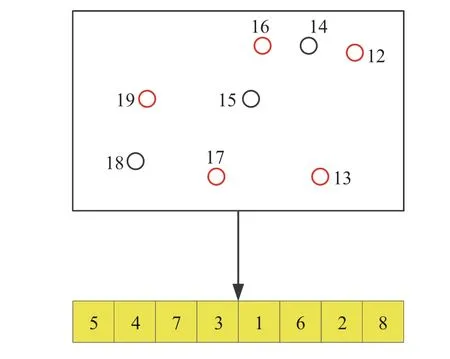
Fig.2 Practicable chromosome representation

However，the basic GA has poor local search ability，making it easy to fall into local optima prematurely. Therefore，the 2-opt algorithm as a pair-wise interchange heuristic[18]is added to solve the EVRPTW in this paper so as to improve the quality of the solution.

Figure 1 presents the flowchart of our method.

4.1 Chromosome representation

A solution to the problem is presented by an integer string of lengthn+k0-1，wherenis the number of nodes，k0represents at most the number of EVs used.We use a sampling area as an instance to indicate the encoding process.All paths are encoded together and a practicable chromosome representation is shown in Fig.2.

In Fig.2，we suppose 3 customers that are black circles;5 nodes along the path which are red circles;at most 1 EV used and the only depot. Then the chromosome can decode one delivery path:0 →5 →4 →7 →3 →1 →6 →2 →8.

4.2 Fitness function

Fitness function plays an important role in GA.GA does not rely on external factors in evolutionary search，instead solely on the fitness function. The fitness value is the main factor to describe the performance of individuals.According to the size of fitness value，the survival of the fittest is carried out on individuals.Fitness function is the driving force of GA.

In general，the larger the fitness value is，the better individuals with higher fitness values are， and the individuals are more likely to be inherited by the next generation. The mapping between the objective function of the optimization problem and the fitness value of individuals.Within this work，the objective function is to minimize the total energy consumption，thus the fitness function is defined as follows:

4.3 Population initialization

Constructing appropriate initial solutions can aid the algorithm in quickly reaching optimal solutions. We first randomly select a customerjfrom all customers，wherej∈N1;at the same time，initialize the number of EVs usedk←1;form a sequence of customers[j，j+1，...，n，1，...，j-1].The number of traversal customers isr，add a customerS(i)to some path，here the loading capacity of EVs must be taken into account. If the path satisfies the loading capacity， we should consider the time window constraints and insert it into an appropriate position.If the path does not satisfy the loading capacity of EVs，we store the customers on the current path，then update another EVk+1.

After constructing the initial solutions，the process is the same as the chromosome representation.As a result，the population initialization can be completed.

4.4 Selection

We let roulette be the method of our selection. The purpose of roulette is that the probability of each individual being selected is directly proportional to the fitness value.We denote some individual asvi， then the selection probability of this individual is

From Eq.(15)，we can see that the higher the fitness value of an individual，the greater the selection probability of the corresponding individual.

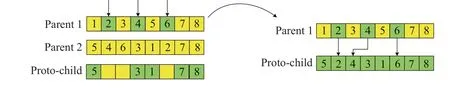
Fig.3 Crossover operator

4.5 Crossover

The crossover operator in this paper is order-based crossover(OBX).In the first step，we randomly select some positions in parents，the position can be discontinuous，but the two parent(yellow)chromosomes are selected at the same position.Here，we choose the position 2，4，and 6，and take parent 1 as an example，and the process of parent 2 is the same.The next step is to find the selected genes of parent 1 in parent 2，while leaving the positions of other unselected genes unchanged.Finally，put the selected genes in parent 1 into the offspring(green) in order. Another offspring can be obtained in the same way.The process of crossover is shown as Fig.3.

4.6 Mutation

In this paper，we adopt mobile mutation as the mutation operator.The mobile mutation is also randomly select a gene，we choose 4; moving one random digit left or right， we move the gene 4 two digits left.The process of mutation is shown in Fig.4.

4.7 2-opt algorithm

2-opt algorithm is an exchange-based algorithm， which is one of the local search algorithms.Given a feasible solution，randomly select 2 positions，reverse the selected segment，as long as the operation can reduce the total power consumed by the EV，the 2-opt algorithm will operate repeatedly until it can no longer be updated，and then a local optimal solution will be generated.In our problem，we select 3 and 6，reverse this selected segment，and a new individual is generated;and by comparing the total electricity consumption of the new generated individual with that of the original individual，the smaller one is chosen.The process of the 2-opt algorithm is shown in Fig.5.

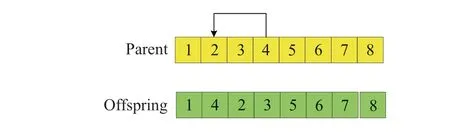
Fig.4 Mutation operator

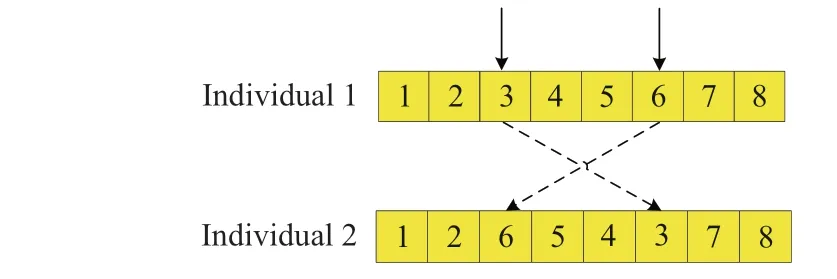
Fig.5 Process of 2-opt algorithm

5 Numerical simulation results

In light of the above our method procedure，the hybrid GA is implemented using Matlab 2016.In this section，we use three size instances VRP10，VRP30，VRP50，which are captured in the Solomon’s data sets(https://www.sintef.no/projectweb/top/vrptw/solomon-benchmark/100-customers/). VRP10 represents that the number of nodes is 10，which contains the nodes of customers and the nodes along the path.VRP30 and VRP50 are represented in the same way.Each size instance we give the comparison simulation results of GA，SA and the hybrid GA.

Before the numerical simulation，we first consider Eq.(1)，for simplify，letf(αi j)= 1+αi jbe a linear function，and¯α=1.The black arrows and red arrows represent the grades of uphill and downhill，respectively.In hybrid GA，the maximum iteration is set to 100，the number of EVs at the depot is set to 3，the probability of crossover is 0.95，the probability of mutation is 0.05，and the electricity capacity of each EV is 50kWh.

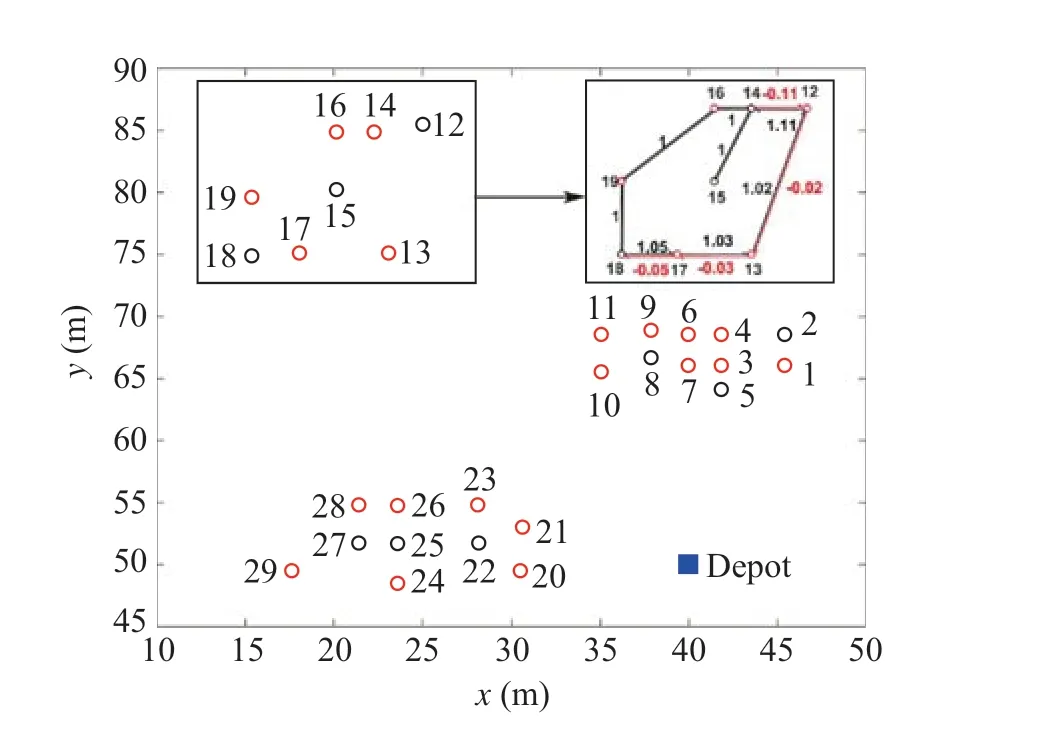
Fig.6 Distribution of each node and the given terrain grades

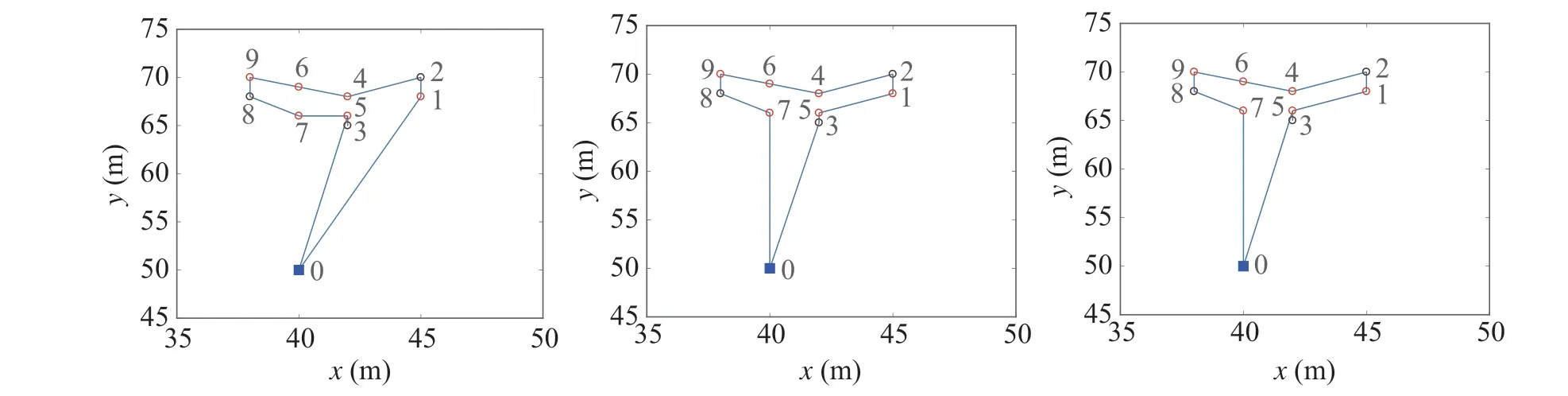
Fig.7 Simulation results of small size instances from c101 to c103

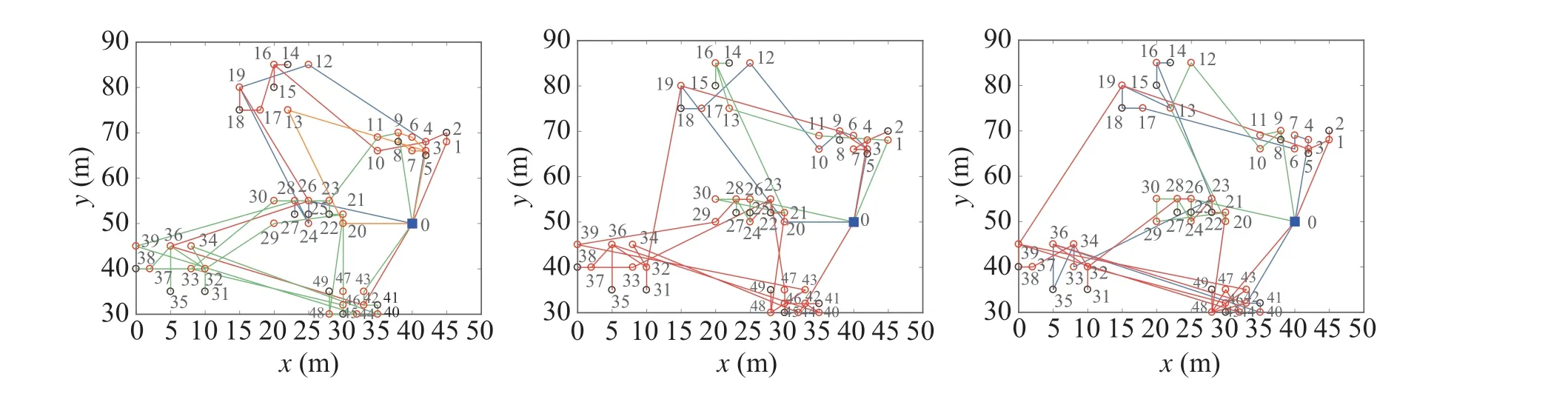
Fig.9 Simulation results of large size instances from c101 to c103

Figure6 shows the distribution of each node in VRP30，and by using a segment as an example to indicate the average terraingrades，other terrains areset inthesameway.Thenode customer we set are 2，5，8，14，15，18，22，25，27.Figures 7，8 and 9 show that three size instances simulated using three Solomon’s data sets from c101 to c103 can be achieved by our method.

In Fig.7，the small size instance contains 10 nodes，where node 2， 3， 8 are customers. Three data sets from c101 to c103 give the optimal delivery scheme only needs one EV.Figure8 shows the optimal schemes of medium size instance with three data sets from c101 to c103.It can be observed that the optimal schemes need three EVs and different data sets because of different delivery routes according to the settings of data sets. Figure9 illustrates the large size instance with three size instances from c101 to c103.The node customer we set are 2，5，8，14，15，18，22，25，27，31，35，40，41，45，and 49.With the increase of nodes，the number of EVs usedby the optimal delivery schemes becomes greater， and the optimal delivery routes become more complex.

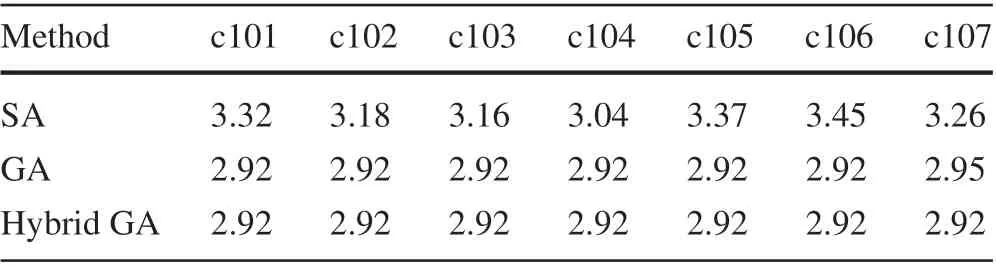
Table 1 Comparison results between GA， SA and Hybrid GA with seven data sets of VRP10

From Tables 1，2 and 3，the simulation results from small size instances to large size instances are given， each size instance contains the results of seven data sets. Column 1 gives the three methods，column 2 to 8 shows the test results from data set c101 to c107，two decimal places are reserved for each test result，and the unit of test results is kWh.

Table 2 Comparison results between GA，SA and Hybrid GA with seven data sets of VRP30

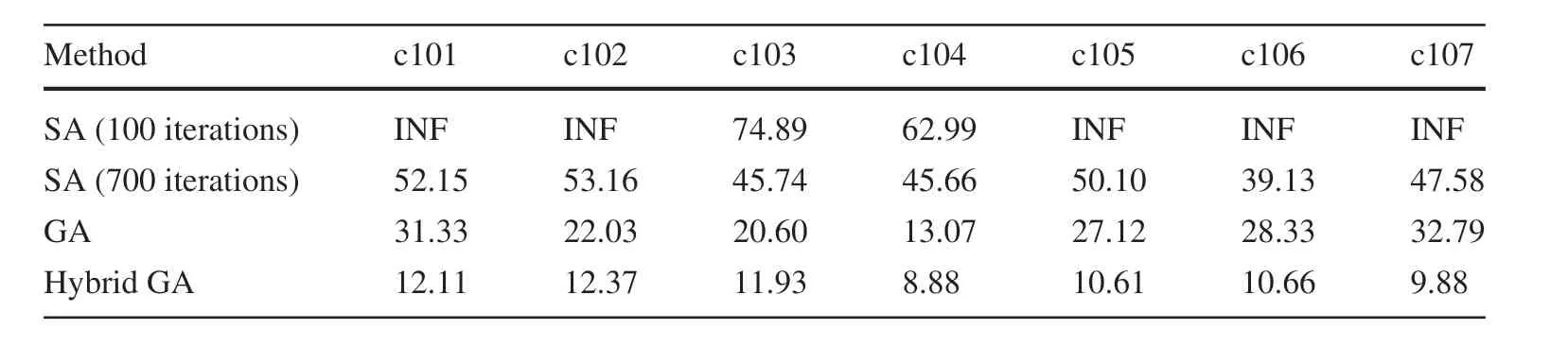
Table 3 Comparison results between GA，SA and Hybrid GA with seven data sets of VRP50

In Table 1， we can see that each method is able to solve the small size of our problem.Furthermore，each test result is extremely close to our proposed approach，which is slightly better.

Table 2 shows the test results of medium size instances.The simulation results indicate that the results of SA seem not so good，and the results of GA are much better than SA.However， the results of our method are still slightly better than GA.From the numerical results，our approach improves the results of SA by over 70% and the results of GA are improved by about 30%on average.

ThetestresultsoflargesizeinstancesareshowninTable3.We can see that when the number of iterations of SA is 100，the results of some data sets cannot run out(INF in Table 3)，i.e.， some problem constraints are not satisfied. Only when the number of iterations is large(such as 700)，can appropriate results be run out.Compared with the 100 iterations of the previous small and medium size instances，when the number of nodes of SA is larger，the solution time becomes longer and the solution quality is not so good.Although the test results of GA are better than those of SA， the improvement of the results is not significant.Our method shows its superiority in large size instances.The results of SA are improved by about 78%，and the results of GA are improved by about 56%on average.

It can be seen that when the number of nodes is larger，our method presents better solution quality.Compared with the simulation results of SA and GA， the performance of our method improves more and more with the increase of the number of nodes， which reflects the advantages of our method.

6 Conclusions

In this paper， we present a new vehicle routing problem to determine consumption-optimal paths for EVs. We formulate the problem as a mixed integer programming model with customer time windows，loading capacity of EVs and terrain grades are incorporated to represent the real-world requirements.

We develop a hybrid GA algorithm that incorporates a 2-opt algorithm into GA for improving the performance of solutions.In numerical simulation results，we first use three Solomon’s data sets to verify our method， and construct a comparison simulation results between SA，GA and hybrid GA.With the increase of node number，the simulation results illustrate that our method has a better performance of the solution.

Thus，our method seems able to successfully apply to the routing decisions for EVs employed in real-world delivery operations.Thiscanalsosupportthespreadingofgreenlogistics practices.

Acknowledgements The authors would like to acknowledge the Toyota Motor Corporation for supports in this work.