Fuel consumption reduction effect of pre-acceleration before gliding of a vehicle with free-wheeling

Wenjing Cao·Taketoshi Kawabe·Tsuyoshi Yuno·Xiaoliang Huang

Abstract Advanced fuel economy strategies are expected to reduce the fuel consumption of vehicles.An internal combustion engine(ICE)driving vehicle equipped with free-wheeling turns off the fuel injection and decouples the engine from the drivetrain when the driving force is not required.This paper proposes a method to reduce the fuel consumption of a vehicle equipped with free-wheeling. First， an optimization problem is formulated to minimize the fuel consumption of a vehicle with freewheeling when the traveling distance，the initial and final speed are specified and the vehicle needs to glide before arriving at the end point for fuel economy. The speed profile of the vehicle， engine operating point， and engine on/off timing are obtained as the results of the optimization.The analytical and numerical analyses results demonstrate the effectiveness and the fuel-saving mechanism of the obtained speed profile.The main finding of the analyses is that rather than starting a gliding stage immediately after an acceleration or a constant speed stage，adding a pre-acceleration stage before the gliding stage is more fuel-economic under some conditions independent of the complexity of the vehicle model.The obtained speed profile including a pre-acceleration stage is applied to a driving scenario including traffic congestions.The results demonstrate the effectiveness of the pre-acceleration stage in reducing fuel consumption for a vehicle equipped with free-wheeling.

Keywords Powertrain·Free-wheeling·Speed profile·Operational mode of engine·Fuel economy·Nonlinear optimization

1 Introduction

Despite renewable energy being adopted globally，petroleum products still account for about 91% of the total energy used in U.S.transportation systems[1].The development of advanced fuel reduction strategies are expected to reduce fuel consumption and air pollution caused by the transportation systems. Extensive research has been conducted to reduce the fuel consumption and emissions [2-7]. The fuel economy of a vehicle with an internal combustion engine(ICE)depends not only on the performance of the powertrain，but also on the driving practice of the vehicle.Subsequently，two categories of fuel-saving strategies have been identified for a vehicle with an ICE.

The first category of fuel-saving strategies includes the development and the implementation of new fuel-saving technologies in the next generation of powertrains. Freewheeling is one of the recently developed fuel-saving technologies[8-10].It turns off the fuel injection and decouples the engine from the drivetrain when the driving force is not required [11-13]. The basic activation strategy of freewheeling is a simple rule-based control method.This method stops the engine according to the pedal operation of the driver and the vehicle speed.It does not consider the traffic conditions.However，the distance to the next stop sign，the distance to the front vehicle，the status of traffic lights may lead to the frequent shifting of the pedal operation of the driver. Consequently，to fully demonstrate the fuel-saving capability of free-wheeling， the traffic conditions must be considered in the activation strategy of free-wheeling.However，to the best of our knowledge，this subject has not been addressed in other literatures.

The second category of fuel-saving strategies involves improving the fuel economy by modifying the driving practices of the vehicles.This involves two approaches.The first approach involves educating the drivers on how to drive the cars economically[14，15].The other involves introducing an automatic powertrain operating system to improve the fuel economy.Although educating the drivers does not result in optimal driving practices， it contributes to 10-15% of fuel saving [15]. Conversely， the second approach operates the powertrain optimally [16-18]. Two specific methods have been researched in previous studies to improve the fuel economy of a vehicle using the second approach. One method involves the optimization of the longitudinal speed profile of a vehicle.This method considering the traffic information when optimize the speed profile of the vehicle to reduce the fuel consumption of it.The second method involves the optimization of the operational methods of the components of the powertrain while tracking a given speed profile.It includes the optimization of the operational mode of the engine，the operating point of the engine， the shifting solution of the transmission，and the gear ratio of the transmission.

In this paper， the two aforementioned methods are combined to optimize the fuel economy of a vehicle with free-wheeling.The proposed method is targeted to be implemented on a vehicle equipped with an automatic powertrain operating system.To obtain optimal fuel economy，the operational method of the powertrain is optimized. The speed profile of the vehicle is obtained as the optimization result but not decided by the driver or specified to follow some driving cycle.

Driving toward the end of a traffic congestion (or a stop sign， a traffic light， etc.) is a potential scenario that free-wheeling can be applied to. In this scenario， the traffic information can be obtained through vehicle-to-vehicle(V2V) or vehicle-to-infrastructure (V2I) communication.The traffic information can be used when modifying the operational method of the powertrain and the speed profile of the vehicle to improve the fuel economy[19-25].In this paper， we first consider the driving scenario when the traveling distance， the initial speed， and the final speed are specified.The initial speed and the final speed are lower than the economic cruising speed of the vehicle.In this scenario，the vehicle must accelerate， and then glide before arriving at the end point for fuel economy. The fuel consumption minimization problem of a vehicle with free-wheeling in the considered scenario is resolved by optimizing the operating points of the components in the powertrain to obtain a fueleconomic speed profile. Since the vehicle is equipped with free-wheeling，the fuel consumption minimization problem in the considered scenario includes two successive phases:the engine-on mode and the engine-off mode.The vehicle is first operated in the engine-on mode and is then switched to the engine-off mode.During the engine-on mode，the vehicle is driven by the engine，which implies that the clutch is engaged，and that the engine generates the driving power.In the engine-off mode， the vehicle glides， which implies that the clutch is released，and that the engine is not ignited.The optimization problem is solved using a numerical method.The effectiveness and condition of free-wheeling to reduce fuel consumption is clarified. The differences between the obtained speed profile and conventional speed strategies，such as constant speed (CS) and pulse and glide (PnG)strategies [26]， are also discussed. To further evaluate the effectiveness of the obtained speed profile， the application of the speed profile in a traffic scenario including two traffic congestion spots is demonstrated.

The rest of the paper is organized as follows: Sect.2 presents the basic assumption and the problem setting.Section3 presents the model of the controlled vehicle and the formulation of the optimization problem. The calculation results for the considered scenarios with different traveling distances are presented in Sect.4.The effectiveness and the fuel-saving mechanism of the pre-acceleration stage and the analysis results are presented in Sect.5.The application results of pre-acceleration stages in a traffic scenario including two congestion spots are also shown in Sect.6.Finally，Sect.7 concludes the paper.

2 Basic setting and assumption

The configuration of the considered powertrain is shown in Fig.1.Four components in the powertrain are considered:an ICE， a clutch， a continuously variable transmission (CVT)，and wheels.

The diagram of the considered scenario，which including two successive phases(the engine-on mode and the engineoff mode)， is shown in Fig.2. In the considered driving scenario，the vehicle starts from the starting point at the given initial speedvstart，drives towards the end point，and arrives at the end point with the final speed，vfinal.The distance between the start and end points is given.Here，assume thatvstart＞0 andvfinal＞0 are smaller than the economic cruising speed of the considered vehicle. In this condition， the vehicle must first accelerate to a higher speed， and then decelerate to arrive at the end point with the final speed to maintain the fuel economy. Therefore， the vehicle must initially operate in the engine-on mode，and then switch to the engineoff mode before arriving at the end point. The scenario is defined such that it represents all candidate application driving scenarios.

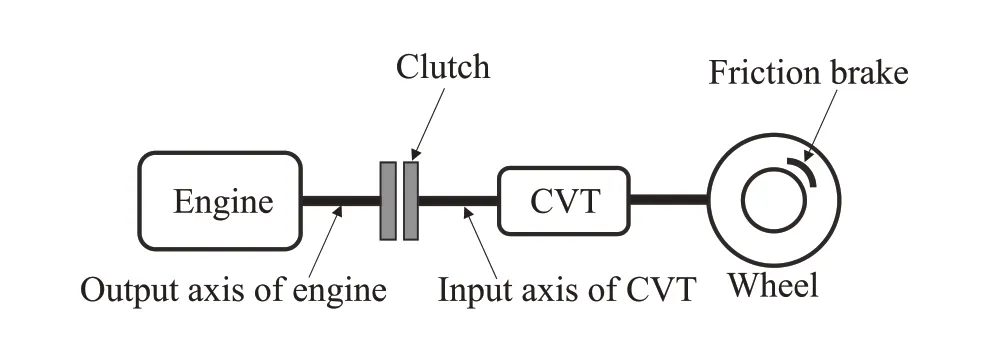
Fig.1 Configuration diagram of the considered powertrain

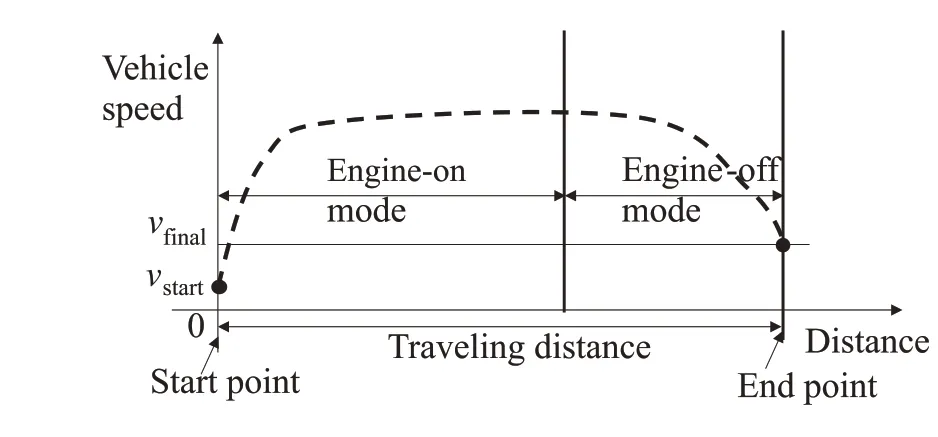
Fig.2 Considered driving scenario

The following assumptions are made to further simplify the problem so that it can be formulated into an optimization problem:

· The problem consists of two phases:the engine-on phase and the engine-off phase. The engine operates in the engine-on mode in the first phase， and operates in the engine-off mode in the second phase.

· There are no traffic lights or obstacles between the start point and the end point.

· The road slope is 0 from the start point to the end point.

· The clutch is always engaged when the vehicle operates in the engine-on mode.

· The clutch is always released when the vehicle operates in engine-off mode，i.e.，free-wheeling is activated.

· The operational mode is switched instantaneously， and no extra energy is consumed during the mode switching(as assumed in[13，27-29]).

· The CVT has a wide speed ratio and is selected to synchronize the vehicle speed and the engine speed when the vehicle operates in the engine-on mode， to ensure that the engine operates in the best brake specific fuel consumption(BSFC)line.

· There is no energy loss from the output axis of the engine to the wheels.

· The dynamics of the components of the powertrain，including the engine，the CVT and the tires，are all disregarded.

· The tires do not slip.

The first assumption is adopted because it is the simplest and themostpracticalwaytooperateavehiclewithfree-wheeling in the considered scenario. In the considered scenario， the engine is switched from engine-on to engine-off mode only once. Furthermore， the fuel consumed during the restart process can be considered as a constant value according to [30，31]. Therefore， regardless of whether the fuel consumed during the stop and restart process is considered，the obtained optimal operational method for fuel economy will be the same. The statement of the above sentence can be expressed using the following equation arg minu J(x，u)=arg minu(J(x，u)+c)，whereJis the fuel consumption of the vehicle，xis the state vector，uis the input vector，cis the fuel consumed during one time of stop and restart process of the engine(a constant value).In the scenario shown in Fig.2，since there is only one time of mode switch，we ignoredcto simplify the problem.

3 Fuel consumption minimization problem

The objective of the optimization is to minimize the total fuel consumption of the vehicle in the scenario shown in Fig.2. This problem can be expressed as the minimization of a performance index subject to the state space equation of the vehicle and the constraints of the state variables，parameters，and control inputs.This optimization problem includes two successive phases according to the operational modes of the powertrain: engine-on phase and engine-off phase. The formulation of the optimization problem is described in the following sections.

3.1 Performance index

The following optimization problem is formulated to minimize the fuel consumption over the problem horizon for the scenario shown in Fig.2:

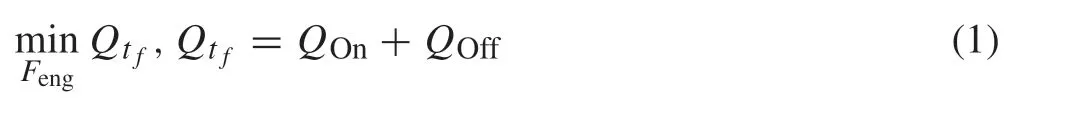
subjects to the state-space equation of the vehicle (5) and other constraints Eqs.(7)-(11).The state-space equation and the constraints are described in later sections of the paper.In Eq.(1)，Fengis the driving force acting on the body of the vehicle，t fdenotes the time when the vehicle arrives at the end point，Qt fis the performance index representing the total fuel consumption in the considered scenario，QOnis the fuel consumption in the engine-on phase，andQOffis the fuel consumption in the engine-off phase. The driving power to generateFengis initially produced by the engine.Under the assumptions introduced in Sect.2，only the fuel consumption of the engine needs to be considered. No fuel is consumed during the engine-off mode since the engine is turned off.Consequently，the following equations are obtained:

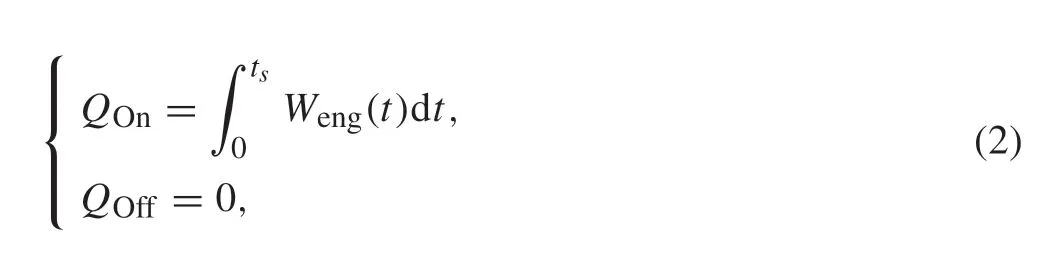
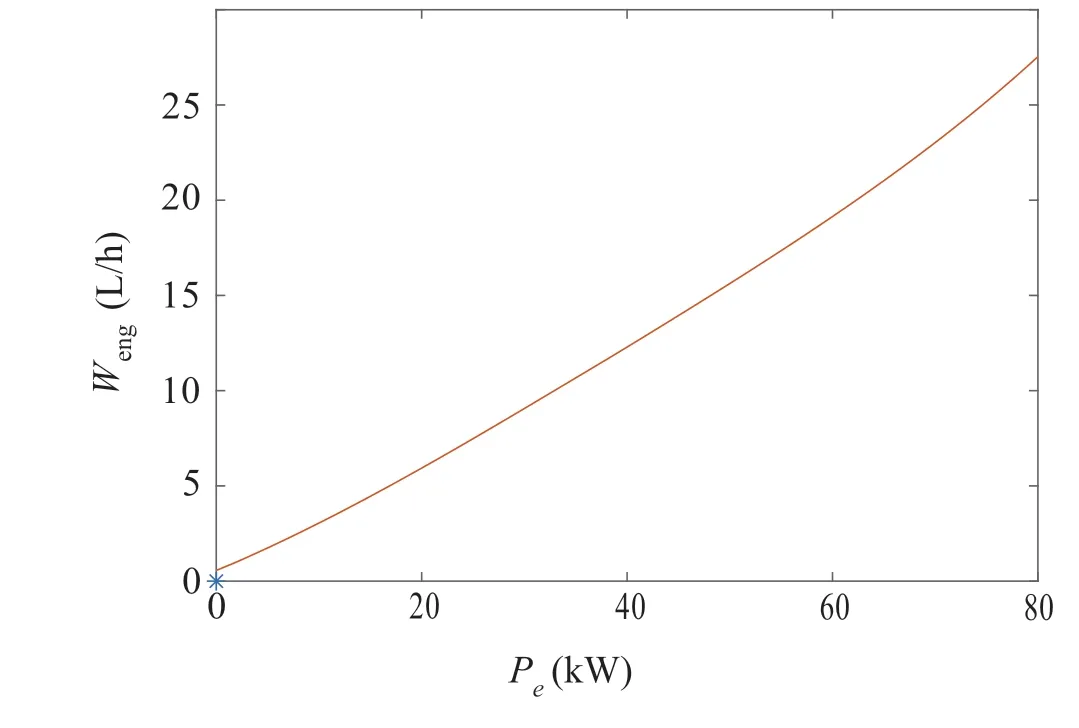
Fig.3 Fuel consumption rate of the engine

whereWeng(t)is the fuel consumption rate of the engine at the timet，andtsis the time when the operation mode of the powertrain is switched from engine-on mode to the engineoff mode.tsandt fare not specified beforehand，but obtained as the optimization results.In this paper，similar to[25，32-36]，Wengis approximated as a polynomial function of the engine power，Pe， according to the static fuel consumption map whenPe ＞0. Only the minimum BSFC line is used for simplicity. Furthermore， considering that the engine is turned off when the driving power is not required，Wengis approximated by Eq.(3):

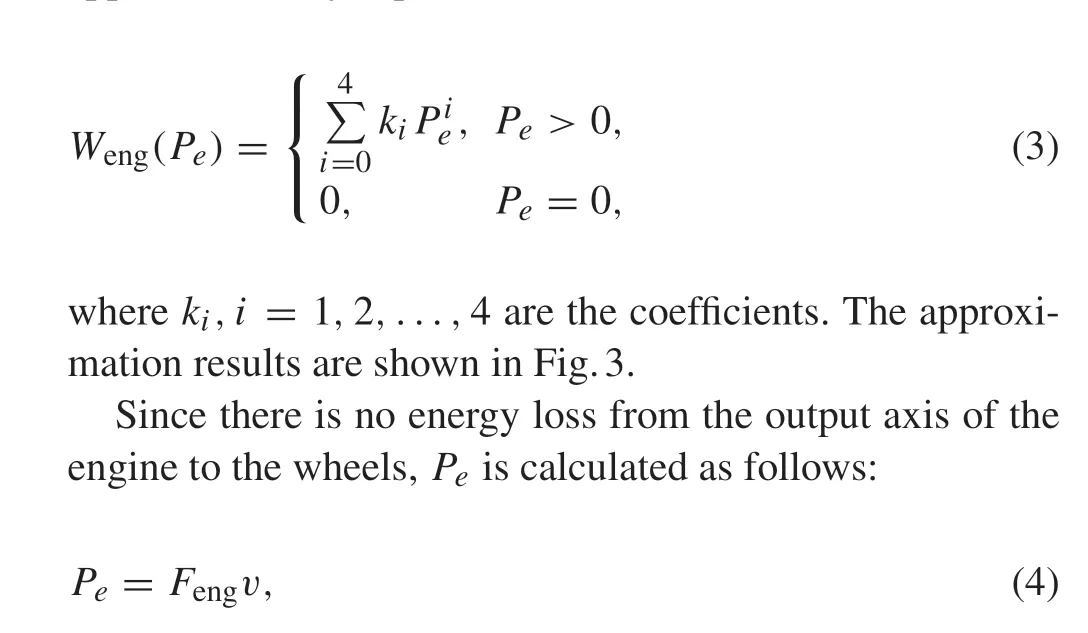
wherevis the vehicle speed.

3.2 State space equation of the vehicle

The mass point assumption is used to simplify the vehicle dynamics and to reduce the calculation load. The obtained vehicle dynamics are expressed as follows:

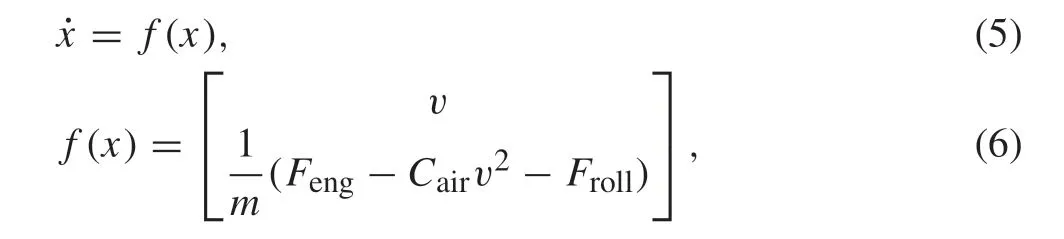
Table 1 Meanings of variables and parameters

wherex= [p v]Tdenotes the state vector andFengis the control input. The definitions of the symbols are listed in Table 1.

3.3 Constraints

The condition of the considered driving scenario and the physical limit of the vehicle are included as the constraints in the optimization problem.

The constraints of the control input，based on the physical limit of the vehicle，are set as follows:

wherevmin，vmaxare the lower and the upper boundaries of the vehicle speed，respectively.As in[38，39]，only the upper and lower limits of the vehicle speed are considered and these values are determined by the road speed limits. The initial constraints of the problem are set as Eqs.(10)and(11):

3.4 Optimization method

The optimization problem includes two phases.It is formulated within the FALCON.m[40]framework and transcribed into a nonlinear programming problem using the direct collocation method.IPOPT，introduced in[41-43]，is used as the solver to numerically solve the resultant optimization problem.

4 Calculation results and analysis

In this paper， eight cases are analyzed to understand the behavior of the optimization results. The only difference among the parameter settings of the eight cases is the traveling distance.The parameter setting and the calculation results are presented in the following subsections.

4.1 Calculation results

The values of the parameters used in the calculations are listed in Table 2.

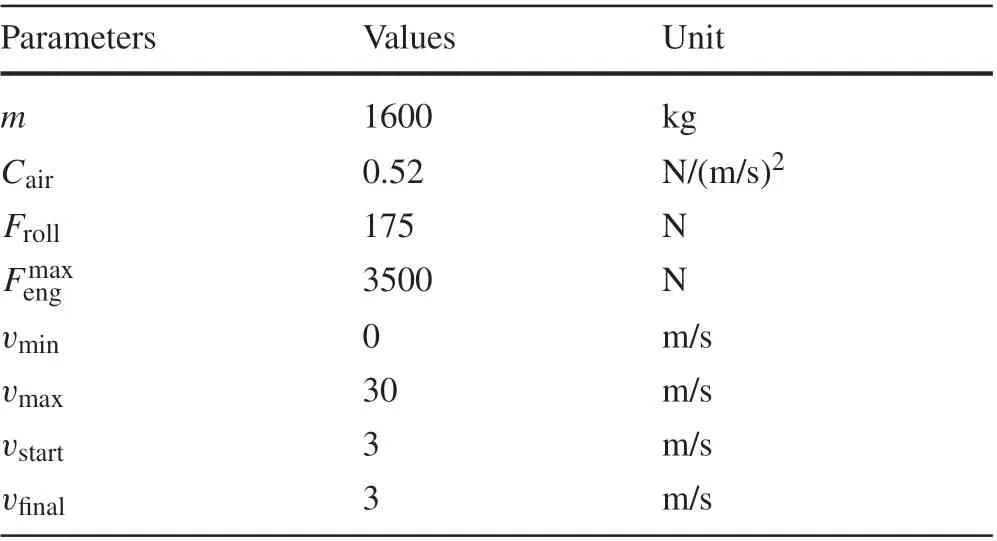
Table 2 Values of variables and parameters

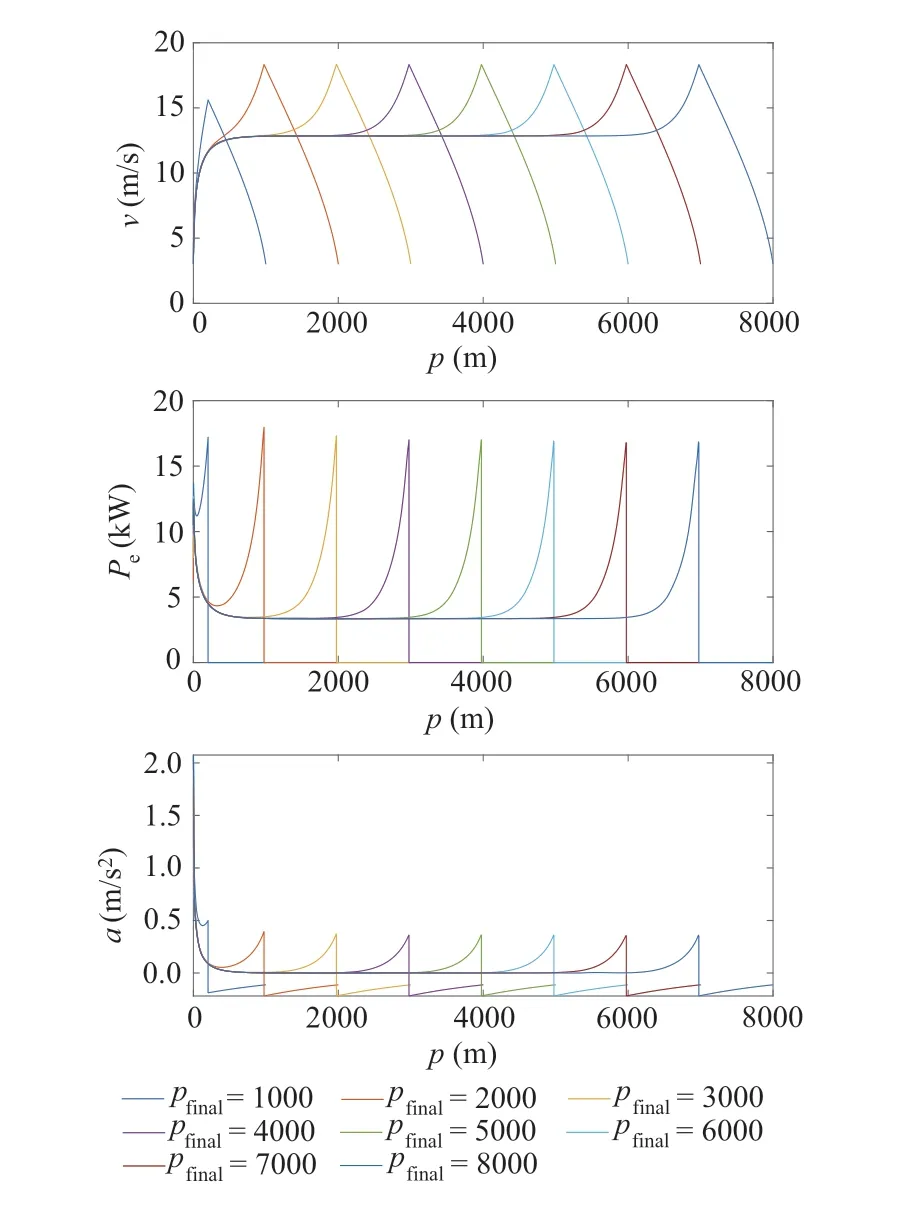
Fig.4 Correlation between traveling distance and other variables

It is observed from Fig.4 that forpfinal= 1000， 2000m the obtained speed profile consists of three stages: acceleration， pre-acceleration， and gliding. For the casespfinal=3000，4000， 5000， 6000，7000，8000m， the obtained speed profiles consist of four stages:acceleration，constant speed，pre-acceleration，and gliding.The gliding stage corresponds to the engine-off phase and the other stages comprise the engine-on phase.

The following conclusions are inferred from Fig.4:

· The acceleration during the pre-acceleration stage keeps increasing until the start of the gliding stage in the obtained speed profile，while in CS and PnG strategies，the acceleration before a glide mode is 0 or larger than 0 but decreasing.

· Whenpfinalis less than a certain value，the fuel-economic speed profile varies according to the traveling distance.

· Whenpfinalis larger than the certain value， the speed profile follows a four-stage pattern.

· There is a pre-acceleration stage in all the obtained speed profiles.

· The cruising speed during the constant speed stage is 12.8m/s. This speed is consistent with the economic cruising speed of the vehicle.

· The maximum speed in the pre-acceleration stage is 18.3m/s， which is higher than the economic cruising speed of the vehicle and is lower than the upper limit of the vehicle speedvmax.

· In the four-stage speed profiles， the speed， the engine power，and the acceleration are the same in the profile for different traveling distances. The traveling distances of the vehicle during the acceleration，pre-acceleration，the and gliding stages arepa= 1074m，pp= 1331m，andpg= 1025m， respectively. The only difference among the speed profiles is the traveling distance during the constant speed stagepc.

Here，definepacaspac=pfinal-pp-pg.pacrepresents the total traveling distance during the acceleration stage and the constant speed stage.The following variable is created to compare the speed profiles during the pre-acceleration and the gliding stages for the different values ofpfinal:

ppgis the traveling distance after the constant speed stage.The correlation betweenvandppgis shown in Fig.5.Figure5 shows that the speed profiles during the pre-acceleration and the gliding stage for different traveling distances are identical.

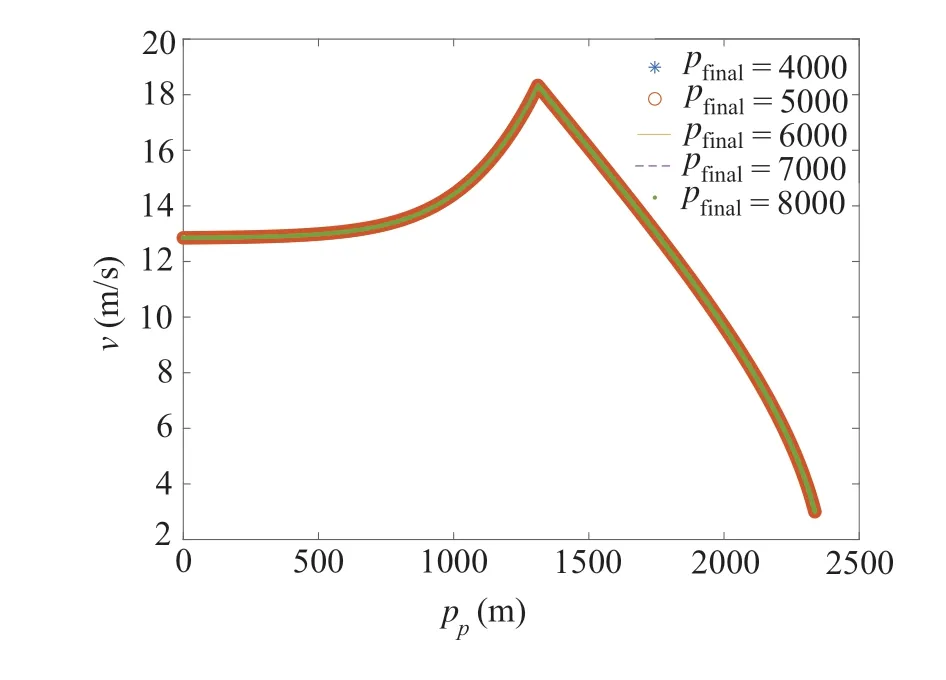
Fig.5 Comparison of speed profiles during pre-acceleration stage for different traveling distances

The obtained fuel-economic speed profile in the considered scenario for a conventional vehicle consists of three stages:the acceleration stage，the constant speed stage，and the gliding stage [25]. This is different from the results obtained for the considered vehicle，which is equipped with free-wheeling.It is observed that optimization calculation is not required to obtain the fuel-economic speed profile for a longer traveling distance due to which， it can be obtained instantly. Therefore， the method used to construct the fueleconomic speed profile can be used in the automatic driving systems of vehicles as a real-time reference speed when traveling between intersections to reduce the fuel consumption.

5 Mechanism analysis of the calculation results

To clarify if and how it is possible to use the obtained results， the effectiveness and the fuel-saving mechanism of the obtained speed profile are analysed in this section. In this section it is assumed that the traveling distance is sufficiently long，and we focus on the four-stage pattern of the speed profile at first. Further， a discussion about the threestage pattern of the speed profile，which is optimal solution for short traveling distance，is given.

The speed profile consisting of four stages is divided into two parts. The first part consists of the acceleration stage and constant speed stage. The second part consists of the pre-acceleration and the gliding stages.Firstly，the optimality of the speed profile in the acceleration stage and the value of the constant speed are validated.A speed profile without pre-accelerationstageisthencomparedwiththespeedprofile including pre-acceleration stage to demonstrate the effectiveness and fuel-saving mechanism of the pre-acceleration stage for vehicles with free-wheeling.

5.1 Optimality of the speed profile in the acceleration stage and the constant speed stage

The analysis method used in [25，47] is adopted to demonstrate the optimality of the speed profile for the acceleration and the constant speed stages. The traveling distance may be different for different speed profiles， even for the same initial and final speeds. Therefore， the traveling distance is set to be equal in order to accurately compare the different speed profiles.The acceleration optimization problem shown in Fig.6 is used to find the optimal speed profile for the considered vehicle during the acceleration stage and the constant speed stage.It is assumed that the vehicle starts from point A with the initial speedv0，accelerates，and arrives at point B at the speedv f.It then cruises with the speedv f，from point B to the destination C.This problem has a fixed initial state，[p0，v0]T，which is independent of the final speedv f，the free traveling distancep f，and the free traveling timetfinal.The total fuel consumption from point A to point C is calculated as follows:

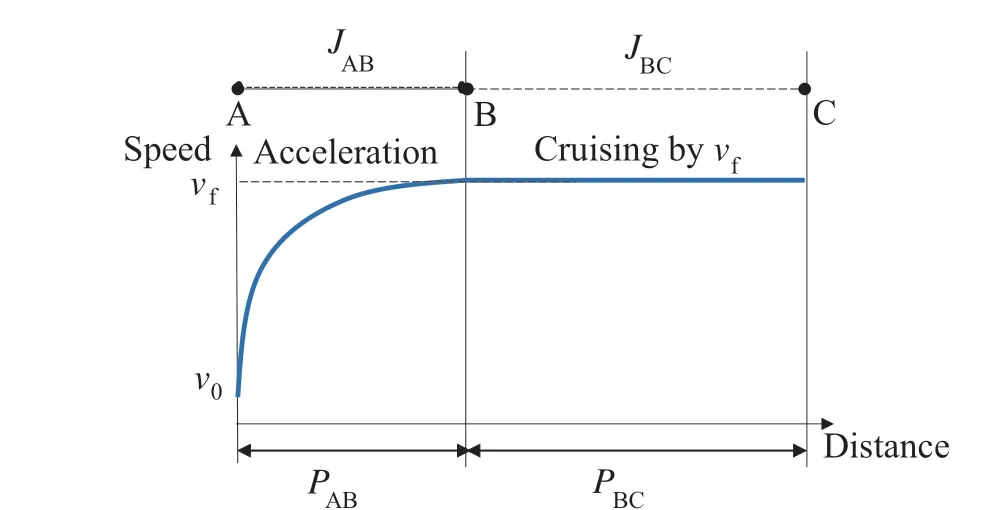
Fig.6 The considered driving scenario in the acceleration optimization problem

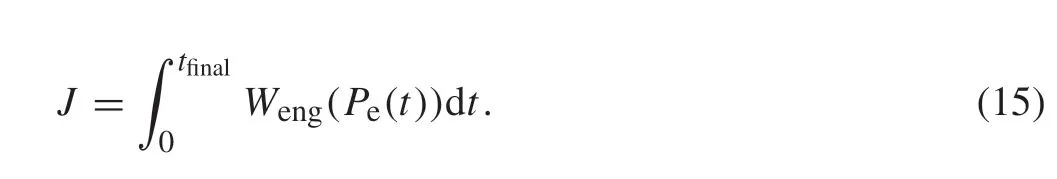
The definition of the scenario shown in Fig.6 ensures that all the resultant acceleration profiles can be considered as a feasiblesolutionoftheproblem.Thesolutiontothefollowing problem yields the optimal speed profile for minimum fuel consumption:

Here，a(t)is the acceleration of the vehicle at timet，andpAC. is the distance between the points A and C. The optimization problem (16) is solved to obtain the optimal acceleration profile which minimize the total fuel consumption in the scenario shown in Fig.6.

The solution to the above problem can be divided into the following three conditions according to the conditions (17)and(18)according to KKT conditions:

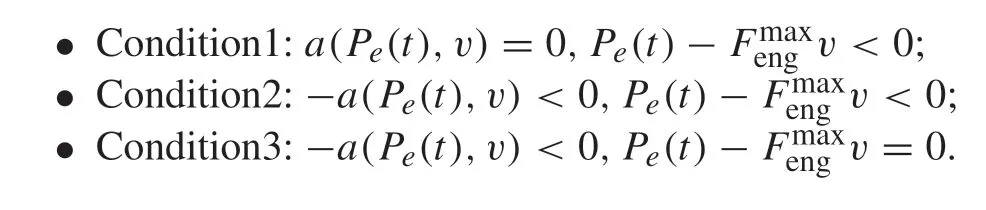
This problem is solved analytically in the same way as in[25，47].

5.2 Compare of analytical and numerical acceleration

Combining the optimal solutions in Conditions 1-3，the optimal acceleration values，aana1，aana2，andaana3are obtained for the different values ofv. The correlations between the vehicle speedv， and the optimal accelerationsaana1，aana2，andaana3，are shown in Fig.7.To compare the results of the numericalcalculationwiththoseoftheanalyticalcalculation，the correlation between the vehicle speed，v，and the vehicle acceleration in Fig.4 are also given in Fig.7.In Fig.7，anumdenotes the acceleration obtained by the numerical method.

Figure7 shows that the acceleration obtained from the numerical analysis is generally consistent with that of the analytical results.Whenv=veco，anum= 0m/s2，which is consistent withaana1. Whenv ＞4m/s，anumis consistent withaana2. Whenv ＜3m/s，anumis consistent withaana3.The difference betweenaana2，aana3，andanumin the interval，v∈[3，4]m/s，is assumed to be caused by the discretization of the original optimization problem in the numerical calculation.This figure proves the validity of the speed profile for the acceleration stage and the constant speed stage，shown in Fig.4.The obtained optimal speed profile during the acceleration stage and the constant speed stage can be implemented when starting up from a traffic light，stop sign，etc.

By the end of the constant speed stage，the engine works in the engine-on mode.The optimal speed profile for the vehicle with free-wheeling is consistent with that of a vehicle without free-wheeling described in[47]because the vehicle has not yet decelerated.Furthermore，the speed profile in the gliding stage is determined by the characteristic parameters of the vehicle.Therefore，it is considered that in the obtained speed profile， the main contribution of free-wheeling in reducing fuel consumption is attributed to the pre-acceleration stage.Therefore，the next step is to clarify the fuel-saving mechanism of the pre-acceleration stage.

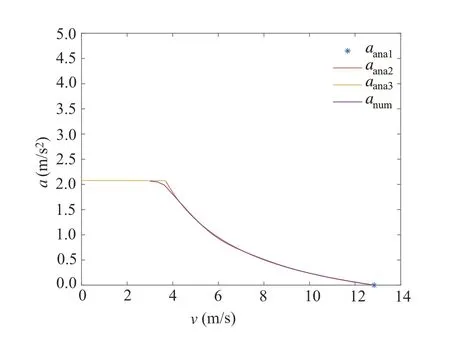
Fig. 7 Comparison of numerically obtained vehicle acceleration and the analytically obtained optimal acceleration

5.3 Effectiveness of the pre-acceleration stage in reducing fuel consumption

In this section， two speed profiles are compared to clarify the effectiveness and the mechanism of the pre-acceleration stage in reducing fuel consumption for the vehicle with free-wheeling.A conventional vehicle without free-wheeling should continue to cruise until the start of gliding mode to minimize the fuel consumption [47]. However， as shown in Fig.4 the vehicle with free-wheeling conducts preacceleration and glides to the end thereafter. These two speed profiles (one includes a pre-acceleration stage， the other one does not include a pre-acceleration stage)are compared numerically to demonstrate the effectiveness of the pre-acceleration stage in reducing fuel consumption.

The overall picture of two speed profiles is shown in Fig.8. It is assumed that the traveling distance of the two speed profiles are bothpfinal. The comparison between the time histories of the vehicle speeds is provided in Fig.9.The speed profile without pre-acceleration is denoted as“No-pre”， and the speed profile including pre-acceleration is denoted as“Do-pre”. These abbreviations are used here after.In Figs.8 and 9pfinal=5000m.The same results can be obtained for different values ofpfinalwhen focusing on the fuel consumption during the pre-acceleration and the gliding stages，as long as the speed profile follows the four-stage pattern.The speed profiles are identical during these two stages for the different values ofpfinal，as shown in Fig.5.

As shown in Fig.9， the speed profiles No-pre and Dopre are identical in the time interval， [0，tp]m. Here，tpis the start time of the pre-acceleration stage. The speed profile No-pre continues the cruising，whereas the speed profile Do-pre starts the pre-acceleration aftertp. Figure10 shows that the maximum difference between the traveling distance of Do-pre and No-pre is 161.4m.This means，when there is a vehicle driving in front of the ego vehicle，the relative distance should be longer than 161.4m to implement Do-pre for fuel economy.161.4m is a comparatively large number in a car-following scenario.Compared with PnG strategy which is suitable for car-following scenarios， it is considered that Do-pre is more suitable for scenarios where there are no front vehicles or the relative distance is longer.Driving toward a red light，a stop sign，a toll gate，or an end of traffic congestion can be given as candidate application scenarios.

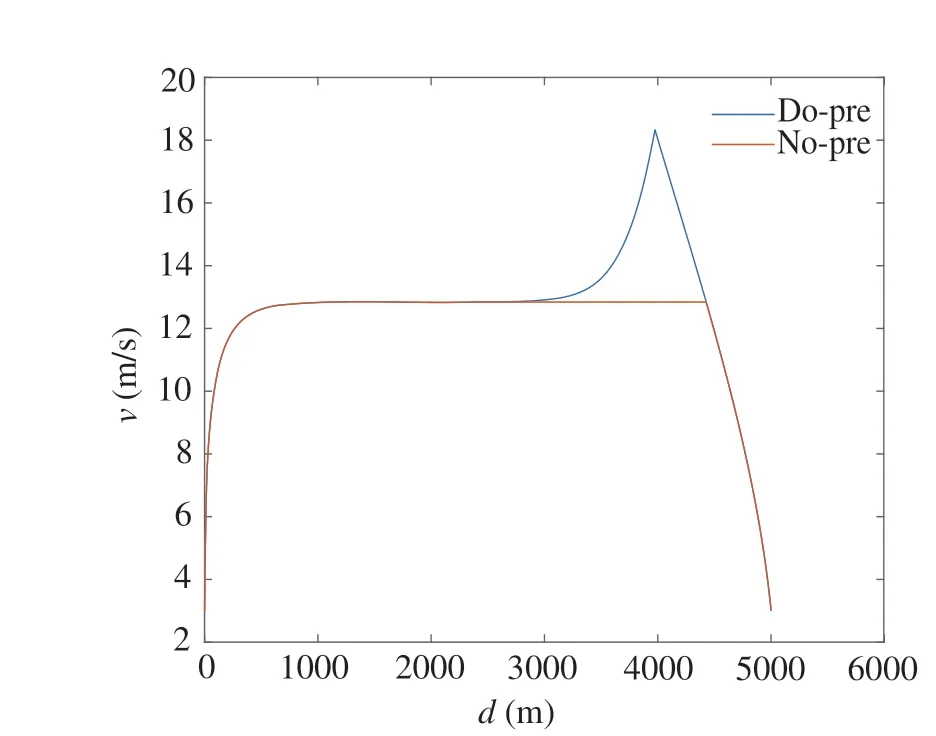
Fig.8 Assumption of the speed profile compare problem

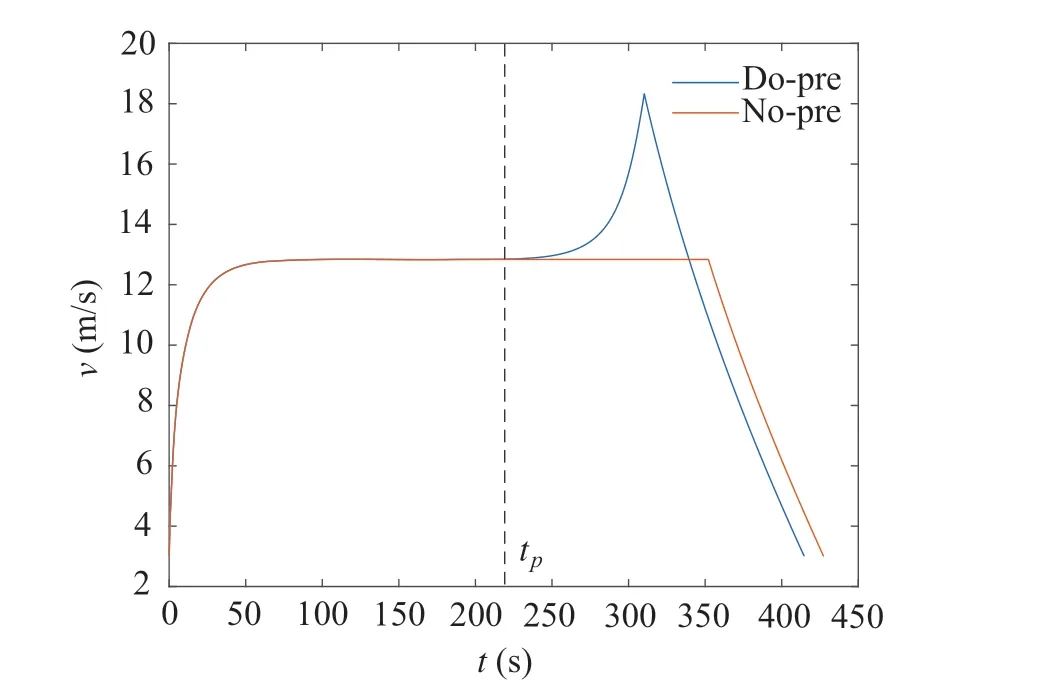
Fig.9 Compare of Do-pre and No-pre

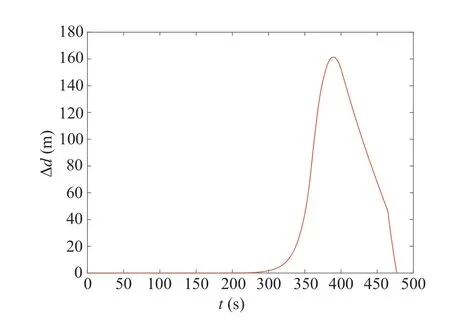
Fig.10 The difference between the traveling distance of Do-pre and that of No-pre

The fuel consumption of the two speed profiles are shown in Fig.11.

Since the two speed profiles are identical by the timetp，their fuel consumption is also identical by the timetp. The difference between the fuel consumption in these two speed profiles occurs after the timetp.When using the speed profile No-pre，it is observed that the vehicle consumes 0.137L of fuel aftertp.When using the speed profile Do-pre，the vehicle consumes 0.134L of fuel. By conducting pre-acceleration，the fuel consumption of the vehicle is reduced by 2.2%.This result demonstrates that the pre-acceleration stage contributes to reducing the total fuel consumption of the vehicle.

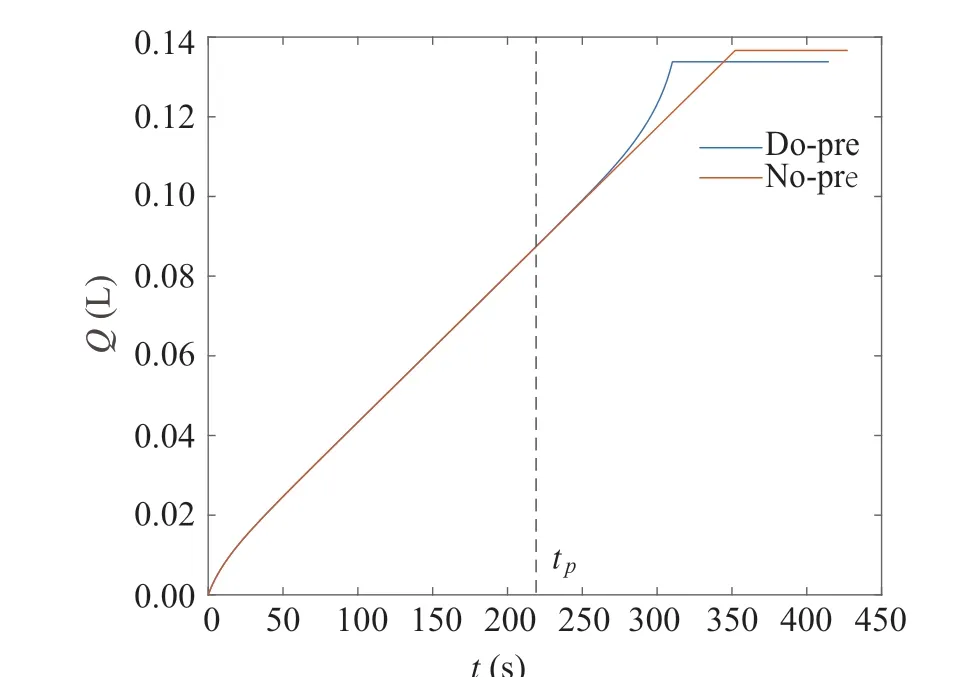
Fig.11 Comparison of the fuel consumption of Do-pre and No-pre

5.4 Mechanism of the pre-acceleration stage in reducing fuel consumption

To further clarify the fuel-saving mechanism of the preacceleration stage，the considered speed profiles are extended from Do-pre and No-pre to Do-prex and No-prex， respectively.The definition of Do-prex and No-prex are as follows:(1) the speed profiles of Do-prex and No-prex during the acceleration and constant speed stages are identical;(2)Doprex includes a pre-acceleration stage before the gliding stage，whereas No-prex does not;(3)the traveling distances of Do-prex and No-prex are the same; (4) the speed profiles during the acceleration， the constant speed stage and the pre-acceleration stages of the two speed profiles do not necessarily consistent with the optimization results shown in Fig.4.The schematic diagram of the two speed profiles after the start of the pre-acceleration stage is shown in Fig.12.A qualitative analysis based on this diagram is given here after.

The nomenclature of Fig.12 is presents as follows. The cruising speed of No-prex is denoted asvc. The following variables correspond to the speed profile Do-prex:tpgis the start time of the gliding stage;tc1is the time when the vehicle decelerates tovc;andteg1is the end time of the gliding stage.The following variables correspond to the speed profile No-prex:tcgis the start time of the gliding stage andteg2is the end time of the gliding stage. As shown in Fig.12，S1，S2，Sc1，Sc2，Sc3，Sg1， andSg2denote the area of each region marked by different colors or lines. The traveling distance of No-prex fromtptoteg2is denoted asp3. The traveling distance of Do-prex fromtptoteg1is denoted asp4.According to Fig.12，

Fig.12 Fuel saving mechanism of the proposed speed profile Do-prex

The fuel consumption of the speed profile No-prex in the time intervals，[tp，tpg]，[tpg，tc1]，[tc1，tcg]is denoted asQc1，Qc2，Qc3， respectively. The fuel consumption of the speed profile Do-prex in the time interval，[tp，tpg]is denoted asQ p.Q pcan be expressed asQ p=Qc1+Qa，whereQais the additional fuel consumption used to produce acceleration during the pre-acceleration stage.The speed profile Do-prex is more fuel-economic than the speed profile No-prex as long asQ p ＜(Qc1+Qc2+Qc3).This condition is equivalent toQa ＜(Qc2+Qc3).The difference between the duration of the engine driving time of No-prex and Do-prex isΔtd=tcg-tpg. Sincev(tp)=vc，Qc2+Qc3=cs(vc)vcΔtd，wherecs(vc)is the fuel consumed to travel 1(m)of distance when driving with the constant speedvc.Notice that even ifvc／=veco，a pre-acceleration stage will still be fuel-economic as long asQa ＜(Qc2+Qc3)holds.

DefineΔtd1=tcg-tc1andΔtd2=tc1-tpg， thenΔtd=Δtd1+Δtd2. In summary， the pre-acceleration reduces the duration of the engine driving time in the following to manners:

· Reducing the duration of the engine driving time forΔtd1by increasing the traveling distance forS1+S2during the pre-acceleration stage and the gliding stage.

· Bringing forward the shut-off time of the engine forΔtd2by increasing the initial speed of the gliding stage.

In summary，Qa ＜(Qc2+Qc3)is the sufficient condition for a pre-acceleration stage to be effective to reduce the fuel consumption. Because this sufficient conditionQa ＜(Qc2+Qc3)is derived by a qualitative analysis，the following remark can be summarized.

Remark 1A pre-acceleration stage is effective to reduce the fuel consumption as long asQa ＜(Qc2+Qc3)holds.

· It does not matter whethervc=vecoor not.

· It does not matter whether Do-prex includes a constant speed stage or not.

· It does not matter whether the acceleration profile during the pre-acceleration stage consistent with the optimization results for the scenario.

· Itdoesnotmatterhowthefuelconsumptioncharacteristic of the engine is approximated or how the dynamics of powertrain is modelled，since the analysis about Fig.12 is not related to the modelling manner of the powertrain.

From the above conclusions，it can be derived that the acceleration profile during the pre-acceleration stage of Do-prex can be adjusted so that it can be applied to driving scenarios where the relative distances between vehicles are less than 161.4m.A precise calculation should be conducted for a specified scenario to ensure that the application of a preacceleration stage contributes to improving fuel economy.

6 Application of a pre-acceleration stage to reduce the fuel consumption

An application example of using a pre-acceleration stage to reduce the fuel consumption is given in this section. The considered scenario is shown in Fig.13.

Considering the condition of the city highway in Tokyo，the parameters for the considered scenario are set as follows:The speed limit is 22.2m/s(80km/h).The vehicle enter the highway at the point A with the initial speed 5.56m/s(20km/h) and exit the highway at the end point F with the speed 5.56m/s.The initial and final speeds are set to 5.56m/s considering the speed limit of an electronic toll collection(ETC)system set at the entrance and the exit of the highway.In the scenario， there are traffic congestion in two places along the way(one between the point B and the point C，the other between the point D and the point E). It is assumed that the distance between each of the two points among A，B，C，D，E，F，and the speeds of the vehicles during the traffic congestions are obtained through V2V and/or V2I communication.For precise information，in this application example，the distances between the points and the speeds during the congestions are specified as follows:dAB=5.00km，dBC=1.00km，dCD= 6.50km，dDE= 0.80km，dEF= 5.00km，vBC= 3.00m/s，vDE= 5.00m/s， whered*+denote the distances between the point*and the point+(*and+represent for two different points among A，B，C，D，E，F).The speed of the vehicle during congestion is specified to avoid being overtaken by other vehicles.The optimal speed profile including three pre-acceleration stages and the speed profile without any pre-acceleration stage are shown in Fig.14.

The speed profiles with and without pre-acceleration stages are denoted as No-prexa and Do-prexa，respectively.It can be observed from the results that Do-prexa includes three pre-acceleration stages while No-prexa does not. The time historyies of the fuel consumption of the two speed profiles are shown in Fig.15.

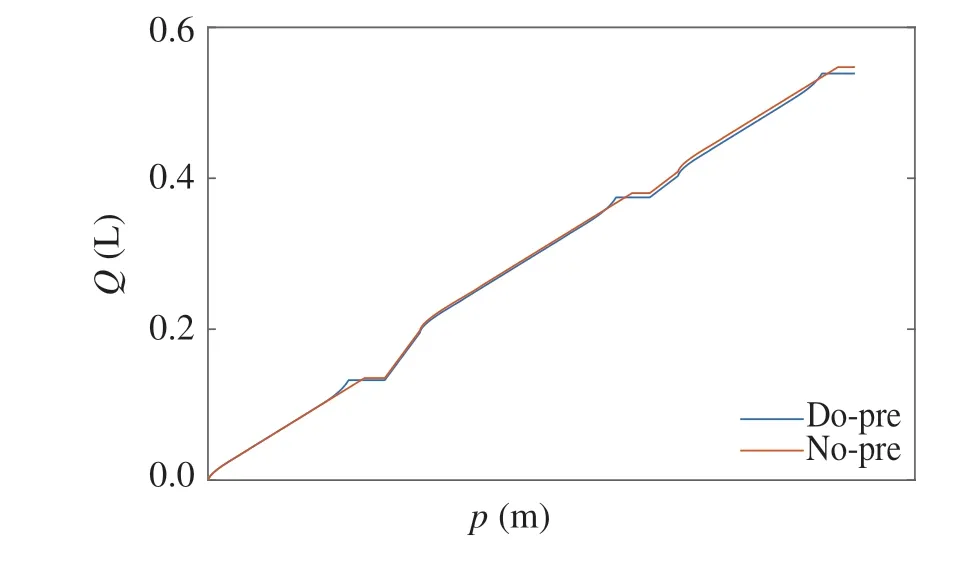
Fig.15 Fuel consumption in the application scenario

It can be observed from the results that in this scenario Doprexa consumed 0.5388g of fuel，while No-prexa consumed 0.5473g of fuel. This means by applying pre-acceleration stage it saved 1.56%of the total fuel consumption.Therefore，it is concluded that the proposed speed profile Do-prexa is more fuel-economic compared with the speed profile without any pre-acceleration stage.

Pre-acceleration stages can be applied in other scenarios to reduce the fuel consumption of the vehicle where there is a deceleration stage.Notice that the acceleration and deceleration might cause a decrease in the relative distance between vehicles.Therefore，when applying a pre-acceleration stage for fuel economy，it should be ensured that the relative distances are long enough.At the same time，the vehicle which is driving behind the considered vehicle should be noted with the speed plan of the considered vehicle，so that the behind vehicle can change its lane or follows a similar speed profile to keep relative distance for safety and fuel economy.The speeds of surrounding vehicles can be predicted to ensure that no accident occurs when implementing a pre-acceleration stage in real traffic as in[48].A precise calculation should be conducted for each case to avoid accidents while improving fuel economy.In a word，pre-acceleration should be applied to a driving scenario where there are no front vehicles or the relative distances between vehicles are comparatively long.Driving toward a red light，a stop sign，a toll gate，or an end of traffic congestion can be given as candidate application scenarios.

7 Conclusions

We proposed a method to reduce the fuel consumption of a vehicle equipped with free-wheeling，which means that the engine can be switched off when the driving force is not required.First，the driving scenario which includes enginedriven and engine off phases is considered.An optimization problem is formulated to reveal the most fuel-economic operating method of the powertrain of the vehicle with freewheeling. The effectiveness of the obtained speed profile in reducing the fuel consumption was demonstrated by the analytical and numerical analysis of the results. A significant finding of the analyses is that rather than starting the gliding stage immediately after the cruising stage， adding a pre-accelerating stage before the gliding stage is more fuel-economic under a condition that is independent of the complexity of the vehicle model.The conclusion holds true even the speed profiles during the acceleration， constant speed，and the pre-acceleration stage are not consistent with the optimization results.Furthermore，the conclusion holds true irrespective of how the powertain is modelled.

To further evaluate the effectiveness of a pre-acceleration stage in reducing fuel consumption，it is applied in a specific driving scenario including two traffic congestion spots.The results validated the effectiveness of using a pre-acceleration stage to reduce the fuel consumption. It should be noticed that when implementing a pre-acceleration stage，the behind vehicle should be noticed about the speed plan of the ego vehicle so that the behind vehicle can change its lane or follows a similar speed profile for safety and fuel economy.

The relation between the traveling distance ahead and the quantity of the fuel that can be reduced by including a preacceleration stage will be investigated to obtain the optimal speed profile in real time.A more precise approximation of the powertrain can be adopted to generate a more practically implementable speed profile for a specified scenario.The fuel consumption and the dynamics of the powertrain during the stop and restart process of the engine will be considered in the future.The effect of the pre-acceleration stage on traffic flow will also be studied in the future.Whether outputing higher engine power before engine stop contributes to reduce fuel economy can be investigated in the future.