Optimization of fuel consumption and NOx emission for mild HEV via hierarchical model predictive control

Yuka Umezawa·Ken Yamauchi·Hiroki Seto·Toshiro Imamura·Toru Namerikawa

Abstract In this paper，we consider the fuel economy optimization problem for a mild hybrid electric vehicle(HEV)using hierarchical model predictive control.In the proposed algorithm，two problems are addressed:eco-driving and torque distribution.In the eco-driving problem，vehicle speed was controlled.Considering the reduction in fuel consumption and NOx emissions，the torque required to follow the target speed was calculated.Subsequently，in the torque distribution problem，the distribution between the engine and motor torques were calculated.In this phase，engine characteristics were considered.These problems differ in terms of time scales;therefore，a hierarchical model predictive control is proposed.Lastly，the numerical simulation results demonstrated the efficacy of this research.

Keywords Mild HEV·Energy management·Model predictive control·Hierarchical control

1 Introduction

In recent years， environmental problems such as the depletion of non-renewable energy resources and global warming have become increasingly serious.It has been predicted that global warming will lead to a rise in global sea levels and changes in meteorological and oceanographic phenomena.Greenhouse gases are a primary cause of global warming.Admittedly， the total amount of greenhouse gas emissions in Japan has been decreasing annually since 2014.However，the reduction target(6%reduction)adopted at COP3 in 1997 has not been achieved. Therefore， issues related to greenhouse gases remain largely unaddressed.

Under such circumstances， the development of vehicles with high energy efficiency and low exhaust emissions is urgentlyrequired.Therefore，hybridelectricvehicles(HEVs)have attracted attention as environment-friendly vehicles.Typically，a HEV is powered by an engine and a motor.Since HEVs use two different power sources， HEVs can reduce the load on the engine， improve fuel efficiency， and reduce exhaust gas emissions compared with general engine vehicles.

Since the main power source is the engine，the vehicle can maintain a long cruising range and because the vehicle can be charged by regenerating the deceleration energy，so it does not require an external power source for recharging.In addition，because the motors and batteries are small，they can be manufactured at a lower cost than EVs.However， although HEVs can improve fuel efficiency，they have complex powertrain mechanisms and limited battery capacity.Therefore，HEVs require proper control schemes.

ManystudieshavebeenconductedonHEVsystems.Since an HEV uses two power sources，it is necessary to consider the optimal power distribution. Various studies have been conducted on this power distribution， such as [1]， which proposes an optimization algorithm based on Pontryagin’s minimum principle.In[2]，a method of applying linear model predictive control was proposed.There are also studies that focus on batteries and battery power management [3]. In these studies，the nonlinear HEV model was linearized considering the calculation cost.However，in several studies，the nonlinearity of the HEV model was considered，and nonlinear MPC was applied.The C/GMRES method was adopted in[4]to deal with the computational cost problem，and East and Cannon[5]used the ADMM algorithm.

Recently，the development of automated driving technology and connected cars has been remarkable，and eco-driving hasbeenconsideredtoimprovefuelefficiencybyconsidering future vehicle speed trajectories based on acquired information related to traffic conditions.In eco-driving research[6]，future traffic conditions based on ambient traffic information and road gradients has been predicted. Moreover， an analysis to learn the schedule pattern of the entire route using machine learning has been reported in [7]. Similarly， the heat load for air conditioning and battery cooling inside the vehicle was considered in [8]. Since there are differences in the time response scales of individual elements，there has been considerable research in recent years aimed at addressing the problem using optimization methods with hierarchical structures.For instance，in[9]，the speed trajectory is considered to be determined according to the driver’s demand.In[10]，multi-horizon MPC was proposed to design an evaluation function that includes multiple horizons in a single optimization problem. Moreover， Uebel etal. [11]proposed a method that combines dynamic programming and Pontryagin’s maximum principle[12]based on available future velocity predictions.Dynamic programming controls the vehicle’s kinetic energy， engine on/off， and gear， given the costates for the battery energy and travel time， wherein the costates are obtained by applying Pontryagin’s maximum principle. However， the behavior of the model soon is not considered. In [13]， a co-optimization scheme is proposed to optimize fuel efficiency for HEVs，using obtainable future speed prediction as the basis to optimally tune control parameters for the existing powertrain control system，but without considering NOxemissions.

Several studies have focused on developing catalysts for exhaust gas research[14-16].In[14]，the NOxremoval rate was improved in a vehicle after-treatment system，and in[15，16]，a method for controlling the ammonia surface coverage of the catalyst was proposed.Additionally，studies on power control have focused on NOxemissions in engines[17-19].A stochastic dynamic programming method for controlling the engine and motor in real time using a Markov driver model was proposed in[17];however，the dynamic characteristics of the engine were not considered.An offline calculation was performed by applying game theory to improve the NOxemissions[18].Moreover，an objective function that considers fuel consumption and engine emissions;by using the dynamic programming method is presented in[19]，and NOxemissions reduced while suppressing the increase in fuel consumption.However，it is difficult to control the system in real time in[18，19].A distributed control design for the energy and thermal management system was presented in [20]， aiming to optimize fuel economy and reduce catalyst warm-up time by cooperation between electrical heating and engine load upshift without considering NOxemissions.To the best of our knowledge，no study has developed a NOxemission model and integrated it into an energy management system to improve fuel efficiency and reduce NOxemissions.

This paper considers the fuel economy optimization problem to improve the fuel economy and reduce NOxemissions.The contribution of this paper is the construction of an NOxemission model and the integration of the NOxemissions model with the energy management system of the HEV to simultaneously achieve improvements in fuel economy and NOxemissions.As an approach，we consider the power distribution problem between the engine and motor and the eco-driving problem.In the eco-driving problem，under the assumption that the target vehicle speed soon is known，the power (torque) required to follow the target vehicle speed is calculated while reducing the fuel consumption and NOxemissions.Subsequently，in the power distribution problem，the distribution of the engine torque and motor torque are determined for the required power.In this process，the characteristics of the engine， such as the fuel consumption and NOxemissions，are considered.At each operating point，the engine torque that is optimal in terms of fuel consumption and NOxemission rate is set，and an evaluation function is designed based on it. As a control algorithm， the distribution of the torque calculated in the eco-driving problem was determined in the power distribution problem. Since these two problems have different time scales， we consider two problems with different time scales and propose a hierarchical control method.

The remainder of this paper is organized as follows.Section2.1 provides an explanation of the fuel economy optimization problem and describes the mild HEV model.In Sect.3， the eco-driving and torque distribution problems are discussed and an approach using hierarchical model predictive control is proposed. In Sect.4， we show numerical simulation results to confirm the approach. Section5 provides a summary of this paper and discusses future issues and prospects.

2 Problem definition

2.1 Fuel economy optimization of HEV

HEVs have two power sources，a motor，and an engine.As such，the load on the engine can be reduced by distributing the driving power required to achieve the target vehicle speed between the motor and engine.When the vehicle decelerates，the motor can regenerate the energy of the vehicle，and can utilize the energy. In this research， the fuel economy optimization problem refers to maximizing fuel economy and minimizing NOxemissions in the driving cycle.

The constraints for speedv(t)(km·h-1)were set as follows to ensure the tracking performance at the target speed:

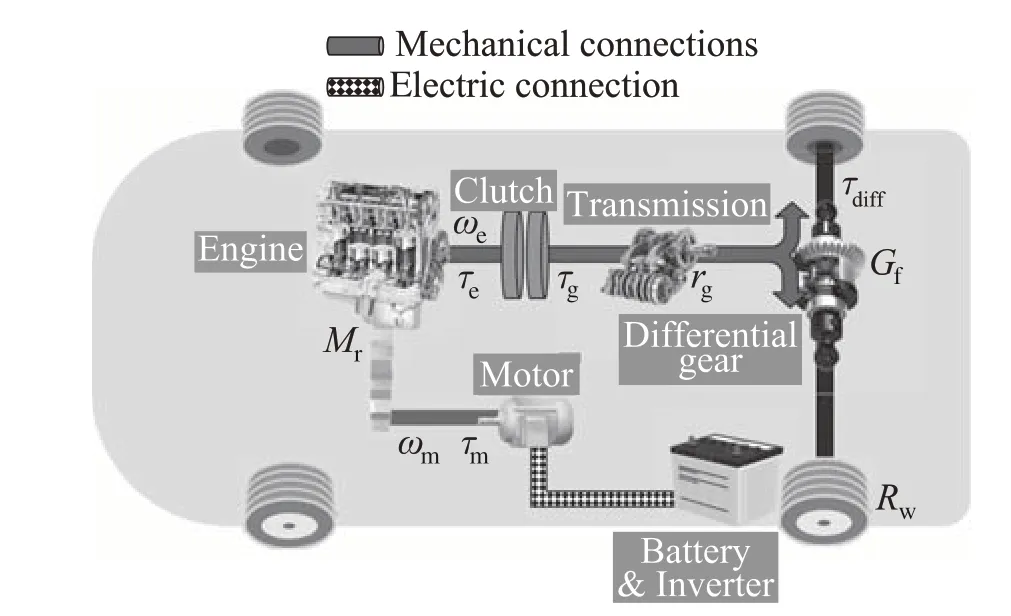
Fig.1 HEV structure

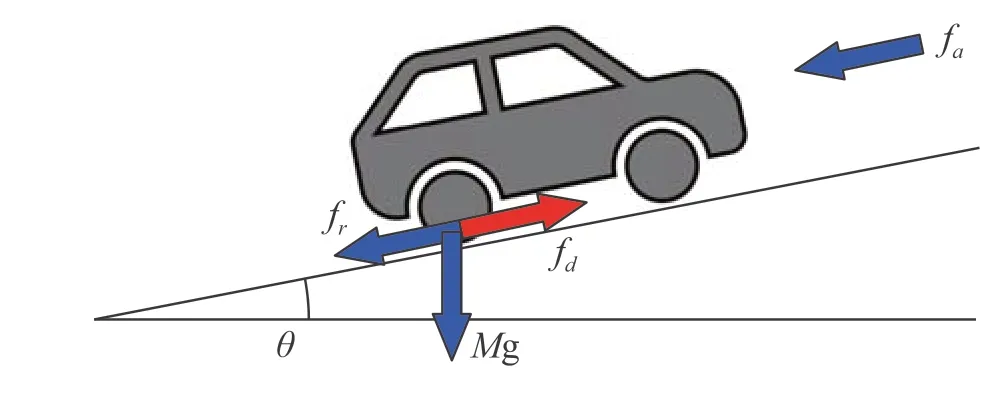
Fig.2 Car force

2.2 Mild HEV model

In this section，we describe the mild HEV model.The structure of a mild HEV is shown in Fig.1. Because the battery capacity of mild HEV used in this research is small， it is impossible to run it only using the motor. Therefore， the engine is always used as the primary power source and the motor is only used as an auxiliary power source.

Next，we model each component of the mild HEV.

2.3 Motion equation of vehicle body

The forces on the vehicle are shown in Fig.2.The equations of motion for the vehicle are shown in Eq.(3).

The definitions of the symbols are listed in Table 1.

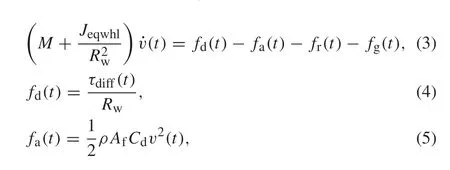
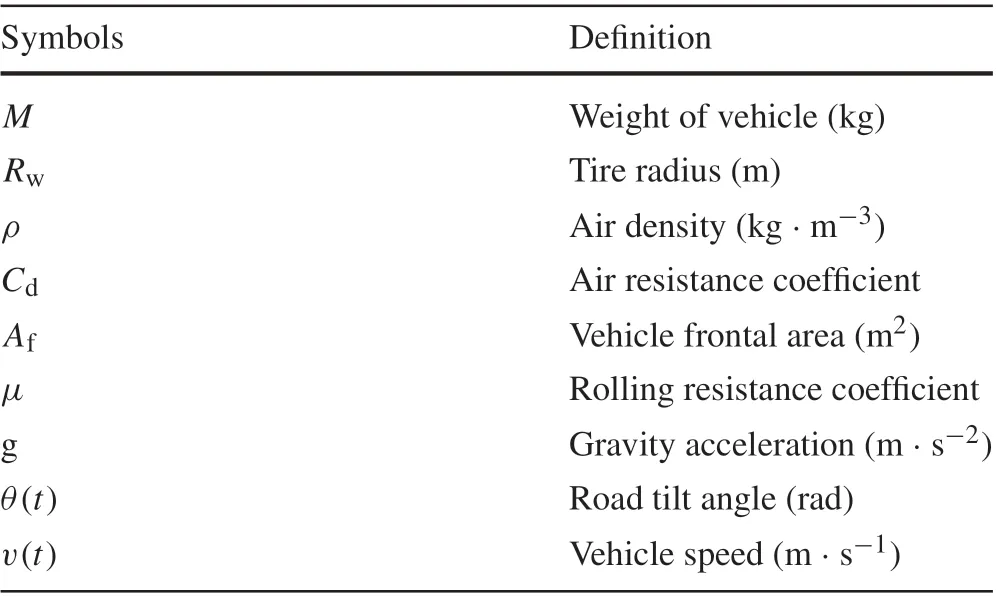
Table 1 Symbols

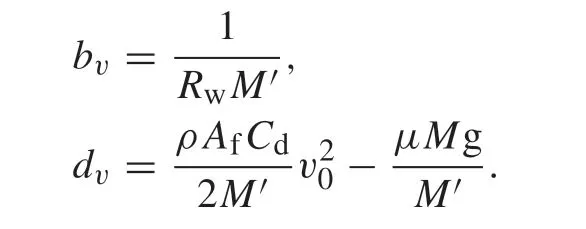
Note thatav，bv，anddvare calculated for each time.

2.4 Input shaft

The shaft that connects the engine to the transmission gear through a clutch is called the input shaft. The propulsion torqueτg(t)is the combination of engine torque and motor torque on the input shaft. Hence， the relationship betweenτdiff(t)andτg(t)can be expressed as

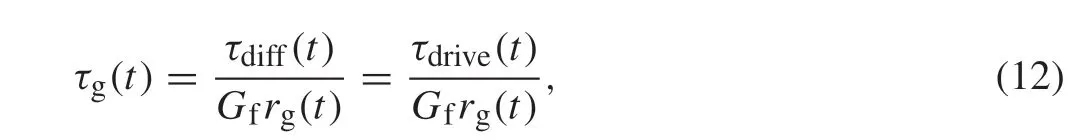
whereGfrepresents the differential gear ratio，rgrepresents the transmission gear ratio，and the engine torque and motor torque are distributed to achieve the required torque，τdrive(t).Subsequently，the relationship between the propulsion torqueτg(t)， the engine torqueτe(t)， and motor torqueτm(t)is expressed as follows:

Mrdenotes the motor gear ratio.Accordingly，τe(t)andτm(t)must be determined to satisfy Eq.(13).

2.5 Engine

Since fuel consumption and NOxemission are critical in the fuel economy optimization problem，we describe them.

2.5.1 Fuel consumption

Using the actual data，we modeled the relationship between the fuel consumptionmf(t)，engine torqueτe(t)，and engine speedwe(t).This relationship is shown in Fig.3 and its equation is shown as

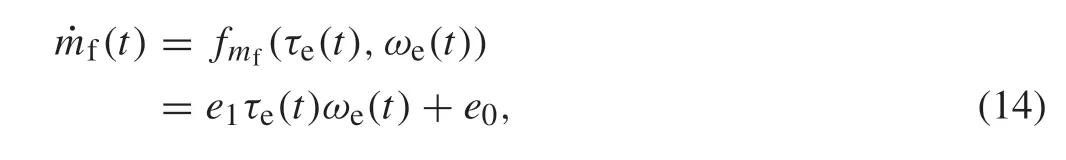
wheree0，e1are coefficients，and the black line is an approximated function.

2.5.2 NOx emission

In addition to fuel consumption， NOxemissions NOx(t)were modeled using actual data. The relationship between engine torque and NOxemissions was analyzed using a set of 18001 data based on actual HEVs.Here，the relation between NOx(t)andτe(t)is described.This relationship is shown in Fig.4，and its equation is shown as

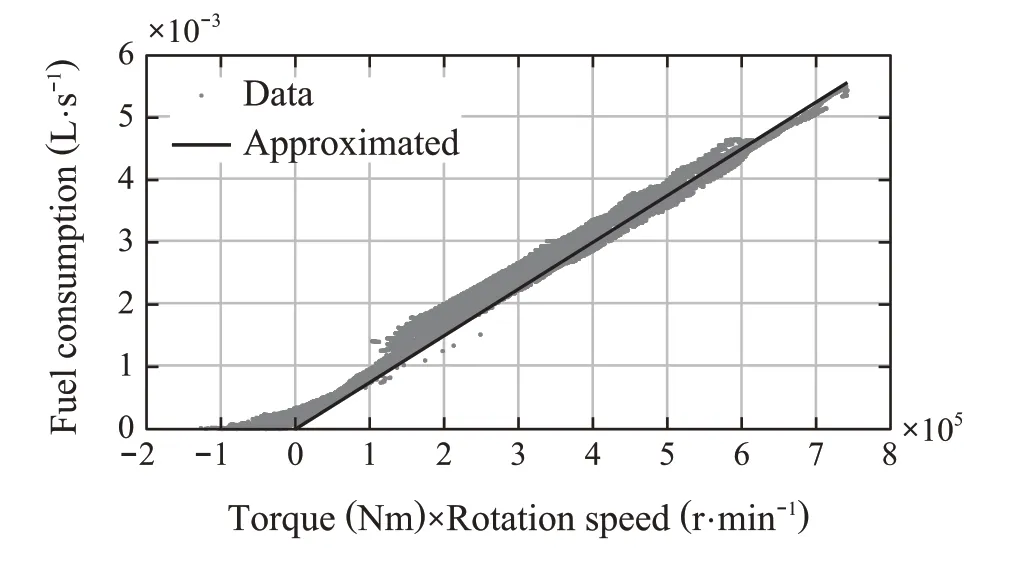
Fig.3 Approximated function of fuel consumption

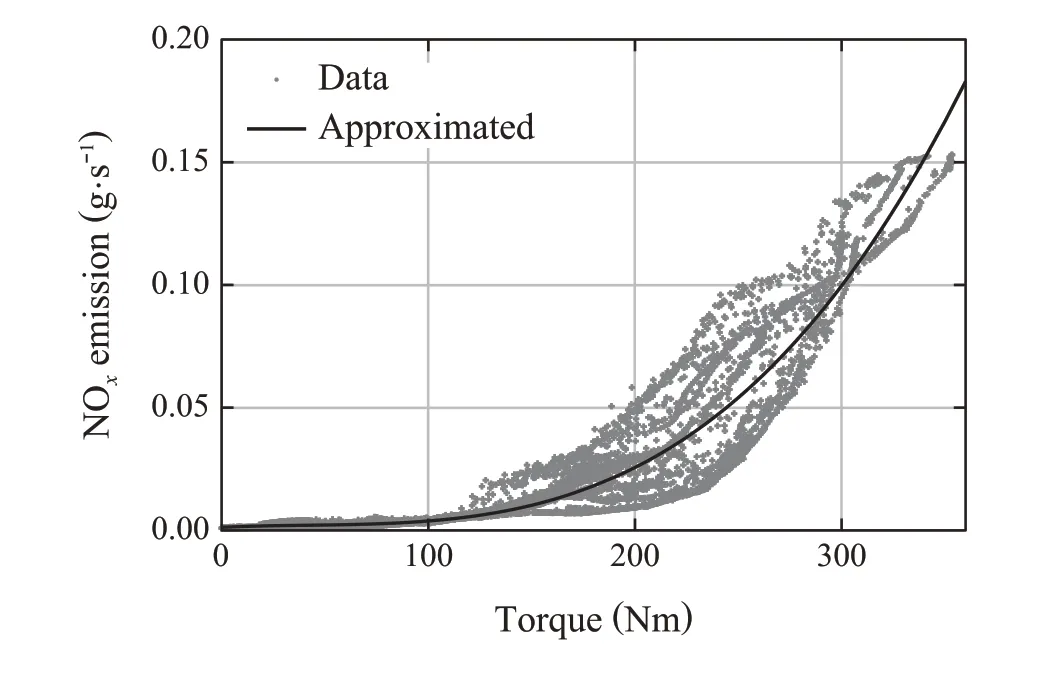
Fig.4 Approximated function of NOx emission

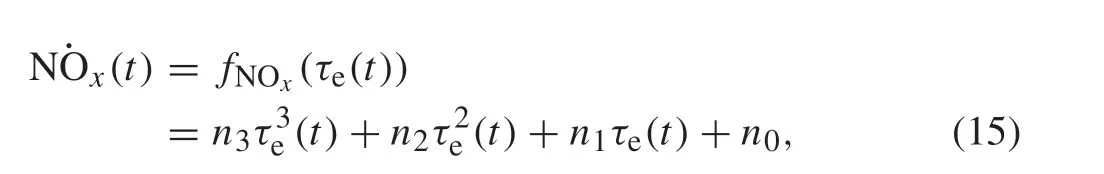
wheren0，n1，n2，andn3are the coefficients，and the black line is the approximated function. We modeled the 3-order function using the least-squares method.However，the above equations are nonlinear，and we derived a linear model equation by linearization.The engine torque at the previous time can be defined asτe(t-1)=τe0to approximate Eq.(15)as follows:

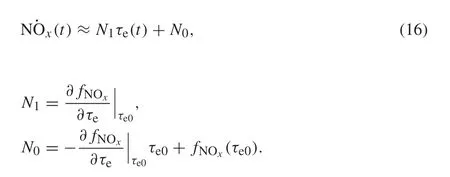
Note thatN1andN0are calculated for each time.

2.5.3 Relationship between driver required torque，fuel consumption，and NOx emissions

The relationship between the driver’s required torque， fuel consumption and NOxemissions are derived based on a model that has been considered so far. ˙mf(k)and ˙ NOx(k)are calculated as follows.From Eqs.(12)and(13)，we obtain

The above model is used in the high-level controller in hierarchical model predictive control.

2.6 Battery and motor

Let the battery output bepbatt， the battery current beIbatt，the voltage beVbatt，the internal resistance beRbatt，and the closed-circuit voltage beVOC，Ibatt(t)can be expressed as follows:

2.7 State-space representation

The relationship between fuel consumptionmf(t)， battery SOC soc(t)， NOxemission NOx(t)， engine torqueτe， and motor torqueτmcan be summarized in the following statespace representation.

Fig.5 Hierarchical control scheme

3 Hierarchical model predictive control

In this section，we describe a fuel consumption optimization method using hierarchical MPC.

This paper deals with two problems: an eco-driving problem that achieves low-load driving through gradual acceleration，and a torque distribution problem that considers the power distribution between the engine and motor.

3.1 Control algorithm

We consider a hierarchical algorithm such as Fig.5.

First，thehigh-levelcontrollercalculatesthetorquerequired by the driver to follow the target speed (eco-driving problem). The speed is relaxed within the constraint range and gradual acceleration is performed， so that fuel consumption and NOxemission are planned to be reduced. Second，the low-level controller determines torque distribution of the engine and motor(torque distribution problem)，in response to the driver’s required torque calculated by the high-level controller.Considering engine characteristics related to fuel economy and NOxemission， the engine torque， which is considered optimal at each operating point， was set. By attempting to drive at the engine torque，Fuel economy and NOxemissions should be improved.Because the time scales handled by the high-level and low-level controller are different，the above hierarchical structure is adopted.

The low-level controller calculates for a short period，The high-level controller performs calculations over a long period. When the actual torque distribution is determined by the low-level controller， the problem is solved with a short sampling time to emphasize the instantaneous operation. However， the future state can barely be considered on a short time scale.However，in the high-level controller，a gradual velocity trajectory is achieved by considering a longer future state.Hence，this problem is solved with a long sampling time. Accordingly， because different time scales should be adapted for the high-level and low-level by using a hierarchical structure，we can consider each time scale.

3.2 High-level controller:eco-driving problem

In this section， we address the problem of eco-driving in a high-level level controller.

3.2.1 Optimization problem

whereHu，1denotes the control horizon，Hp，1corresponds to the predictive horizon，vref(k+i)is the vehicle speed target value and ˆv(k+i)denotes the predicted vehicle speed.The first equation of Eq.(34)is a discretization of Eq.(11)with sampling timeTs，1.

The first term represents the difference between the target vehicle speed and predicted vehicle speed， the second term represents the terminal cost related to the first，the third term represents the fuel consumption， and the fourth term represents NOxemissions.Hence，the first item is related to the tracking of the target vehicle speed， and the third and fourth items are related to the reduction in fuel consumption and NOxemissions，respectively.However，in the case of reducing fuel consumption and NOxemissions，reducing fuel consumption and NOxemissions，reducing the driver’s required torqueτdrivemay cause the vehicle speed to always fall below the target speed to satisfy the lower bound constraint.The terminal cost was set as the second item to avoid the problem mentioned above. In the eco-driving problem，by fixing the motor torqueτmto the previous value，it is possible to solve the problem without considering the battery SOC.

3.3 Low-level controller:torque distribution problem

In this section，we address the torque distribution problem in the low-level level controller.

3.3.1 Optimization problem

In the torque distribution problem，energy management that optimally distributes power to the motor and the engine shouldbeachievedtosatisfythedriver’storquerequirements，improve the fuel economy，and reduce NOxemissions.During acceleration， the engine is operated at a load with high efficiency and motor power is used to assist the engine.During deceleration， the battery was charged via regenerative braking.Therefore，we consider the following optimization problems:

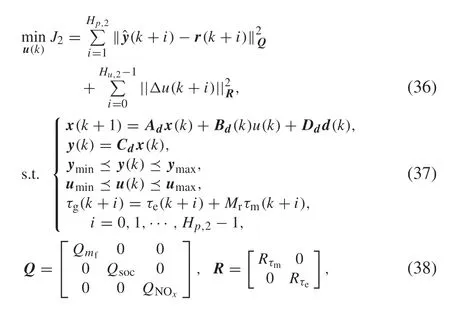
whereHu，2denotesthecontrolhorizon，Hp，2denotestheprediction horizon，r(k+i)signifies the state reference value，ˆy(k+i)denotes the predicted output，andΔu(k+i)corresponds to the input change.

The first and second equations in Eq. (37) are the discretization of Eq.(31)with the sampling timeTs，2.Equation(36) minimizes the difference between the state and target state values and the amount of input change.The target state value should be properly set.

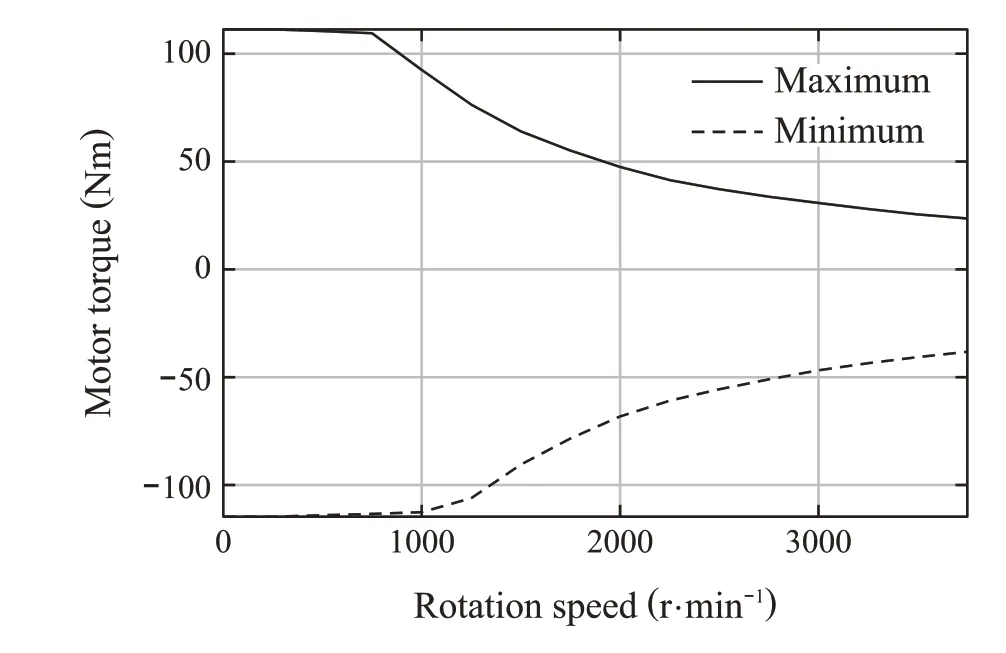
Fig.6 Constraint of motor torque

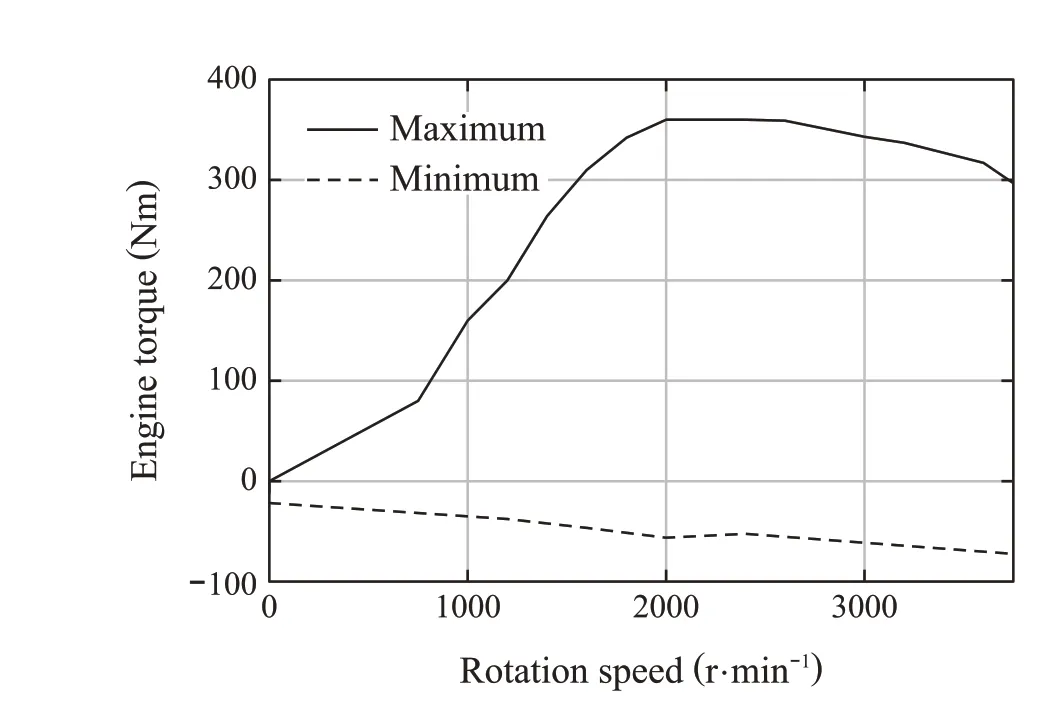
Fig.7 Constraint of Engine torque

Furthermore，ymin，ymax，umin， andumaxrepresent the lower and upper bounds of the state and input，respectively.The input constraints depend on the rotation speed，as shown in Fig.6 and Fig.7.

But as he looked one of them silently drew a white sash from her pocket and slipped it round her waist, and the young man sprang to her and said, This is the princess, and I claim her for my wife

3.3.2 Reference setting

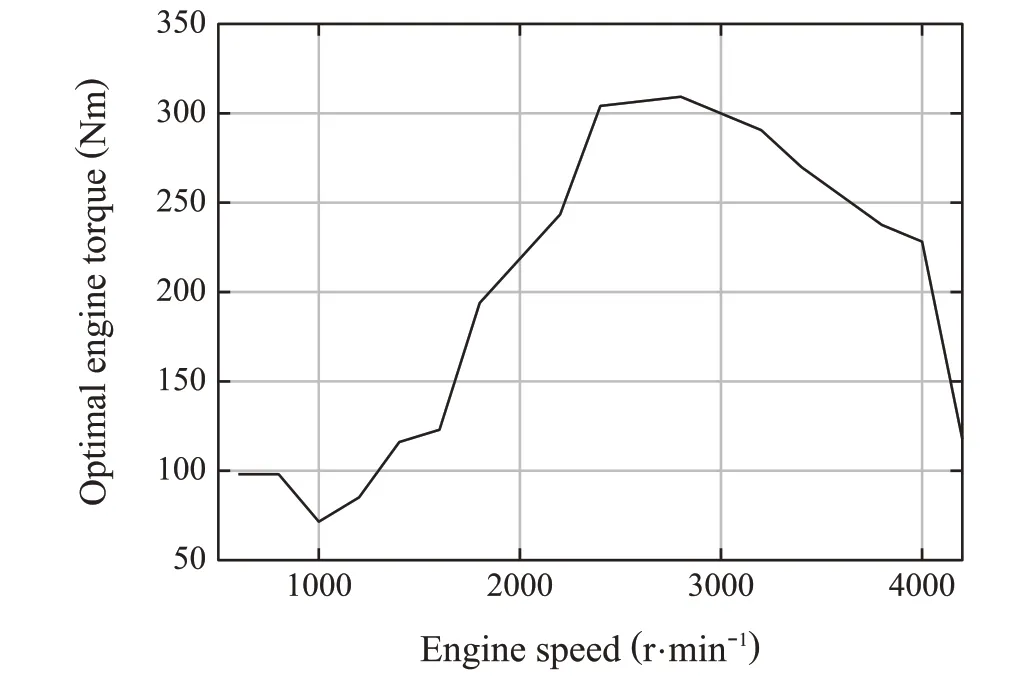
Fig.8 Optimal engine torque for each rotation speed

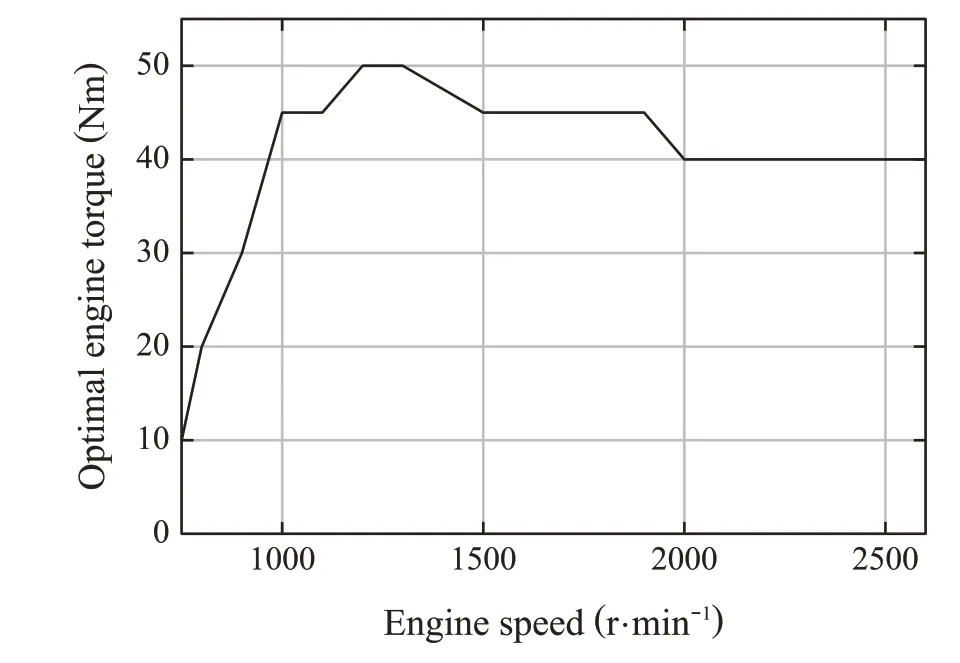
Fig.9 Optimal engine torque for each rotation speed

4 Simulation

4.1 Simulation condition

In contrast to the mathematical model for the control system design presented in Sect.2，the model for the simulation in this section is a large-scale complex multilayer system with nonlinearities， logic， and discontinuities. It is very similar to that of a real vehicle. The simulation environment was developed in MATLAB/Simulink.

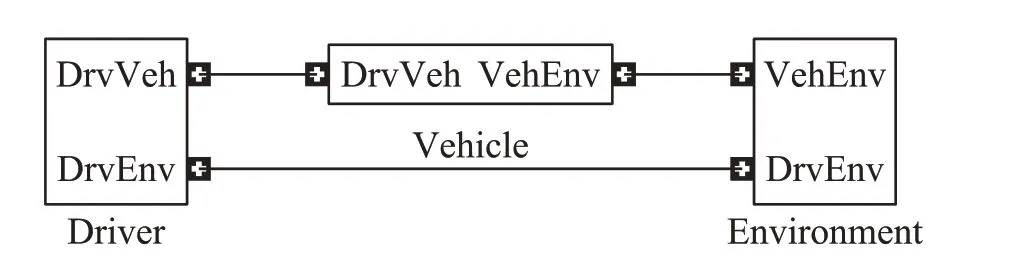
Fig.10 Basic structure of HEV simulation model

The simulation model consists of a driver，engine control，and vehicle plant models，including the engine and NOxcatalyst. The driver model addresses the eco-driving problem and calculates the driver required torque to follow the target speed.Moreover，the engine control model controls the engine by determining the control values for the engine plant models of fuel and intake/exhaust systems through feedback control based on the gas pedal signal from the driver model and engine speed， temperature， pressure and flow signals.The engine plant model uses the mean value engine model(MVEM) for each piping and turbocharger， and the diesel combustion model is a map model.Part of the vehicle model in MATLAB/Simulink is shown in Figs.10 and 11.

The computer used for the simulation comprised a 2GHz quad-core Intel Core i5 processor with 16GB 3733MHz LPDDR4X memory. The simulation was conducted under the assumption that the Worldwide harmonized Light duty Test Cycle(WLTC)as the driving mode，as shown in Fig.12.WLTC is an international fuel efficiency test method called“Worldwide Harmonized Test Cycle.” Figure12 illustrates the reference speed of the vehicle d.

The design parameters，including the weights of the evaluation functions，are presented in Table 2.

Constraints on vehicle speedsvmin，vmaxwere set to a smaller value considering the modeling error. The battery SOC constraints socminand socmaxwere 20% and 90%，respectively.Additionally，if the battery SOC changes from its initial value， generally it is difficult to compare the fuel economy.Therefore，the fuel consumption was calculated by considering the fuelmf.soc，which corresponds to the amount of charging difference from the initial value.mf.socwas calculated as follows:

whereQLHVdenotes lower heating value，ηerepresents the engine thermal efficiency，ηmcorresponds to the power efficiency，SOCinidenotes the initial SOC，SOCendrefers to the final SOC，andQsocshows the battery capacity.

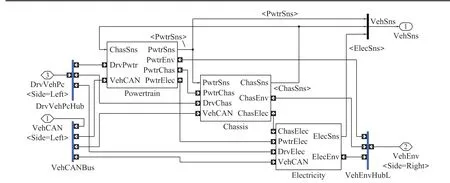
Fig.11 Vehicle plant and controllers

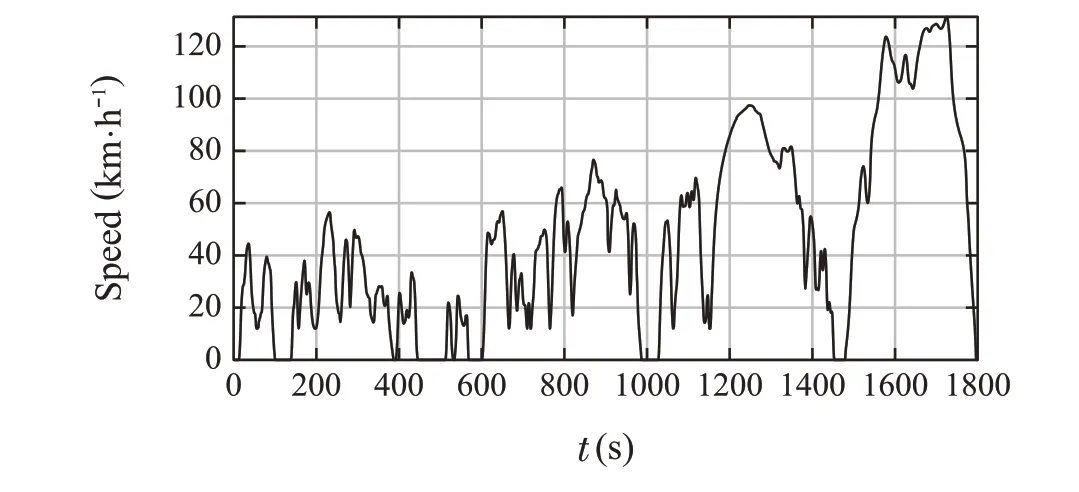
Fig.12 Vehicle speed(WLTC mode)

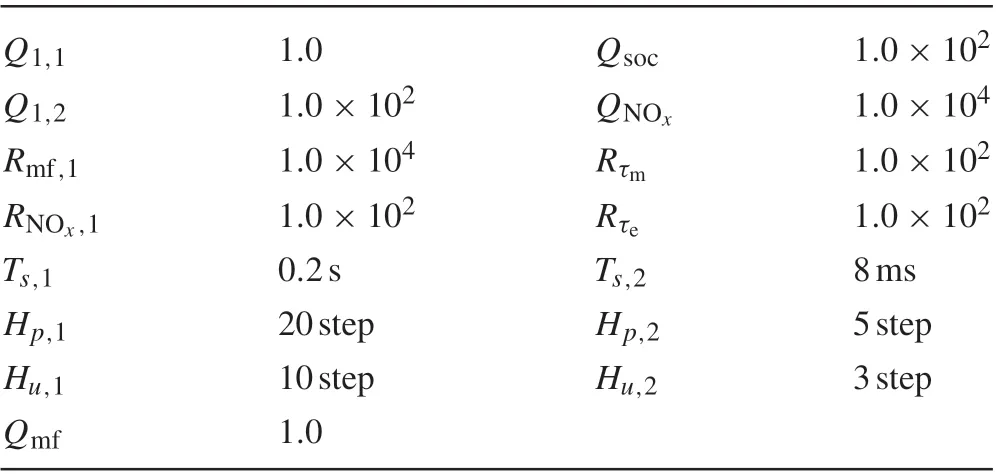
Table 2 Design parameters

In this paper，we compared the proposed method with the rule-based method as a conventional method. In the rulebased method，transitions are made according to the rules for each mode (motor assist， regenerative， and driving charge modes).

Moreover，the amount of assistance and regeneration was calculated.Forspeedcontrol，thedriver’srequiredtorquewas calculated by proportional-integral-derivative(PID)control from the difference between the target vehicle speed(target acceleration)and the actual state.

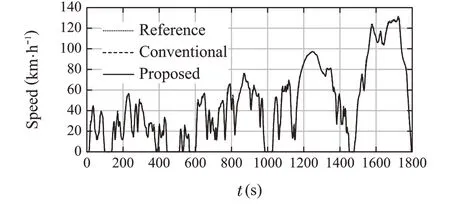
Fig.13 Vehicle speed

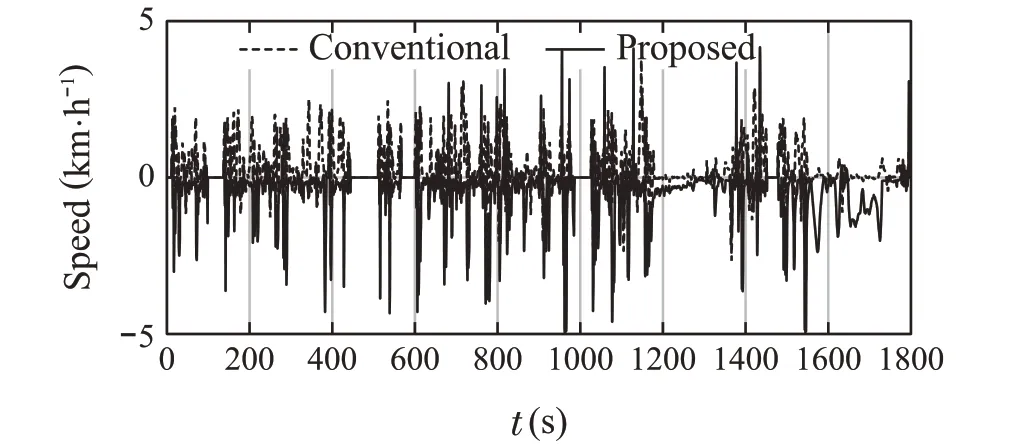
Fig.14 Vehicle speed difference

4.2 Simulation results

The actual time required to solve the problem was 1047s for a running simulation of 1800s.From these results，we believe that the proposed control law can be implemented effectively in real time.The simulation results are as follows.Figure13 depicts the vehicle.Figure14 shows the difference from the reference speed， and the numerical results are summarized in Table 3.

Figures13 and 14 show that the speed constraint is satisfied. And from Table 3， the fuel consumption is slightlyimproved， and NOxemissions are remarkably improved.Some of them are as follows to confirm the detailed results of the proposed method.

Table 3 Simulation results

Fig.15 Vehicle speed(1470-1800s)

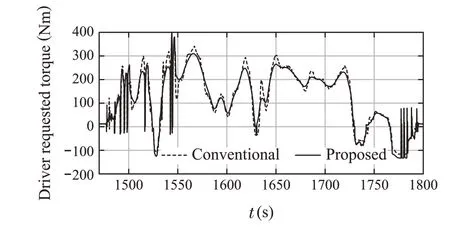
Fig.16 Driver requested torque(1470-1800s)

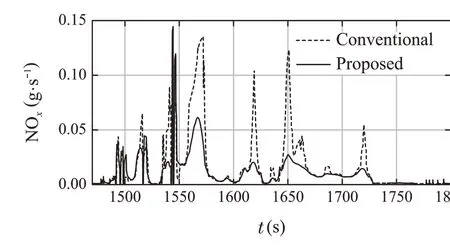
Fig.17 NOx emission(1470-1800s)

From Fig.15，it is evident that the tracking of the vehicle speed is achieved.It can be confirmed that speed control is performed in such a way that acceleration is gradual.From Fig.16，although there is no significant change in the required torque of the driver， it can be confirmed that the points with high loads are cut off. In other words， the operating points with high loads and NOxemissions were significantly reduced(Fig.17).In addition，a small reduction in fuel consumption was achieved according to the required torque(Fig.18).

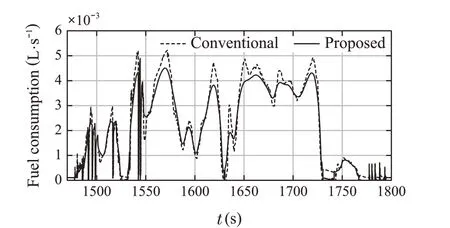
Fig.18 Fuel consumption(1470-1800s)

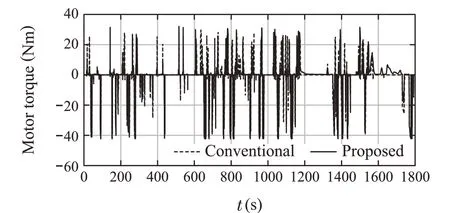
Fig.19 Motor torque

Finally，the results for all simulations(1800s)are shown below for the motor torque，battery SOC，engine torque，fuel consumption，and NOxemissions.

5 Conclusion and future works

Fig.20 Battery SOC

Fig.21 Engine torque

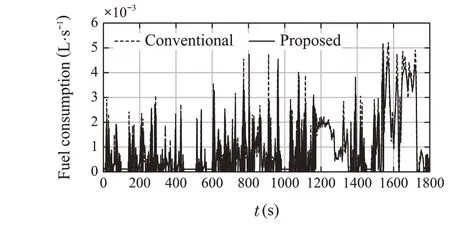
Fig.22 Fuel consumption

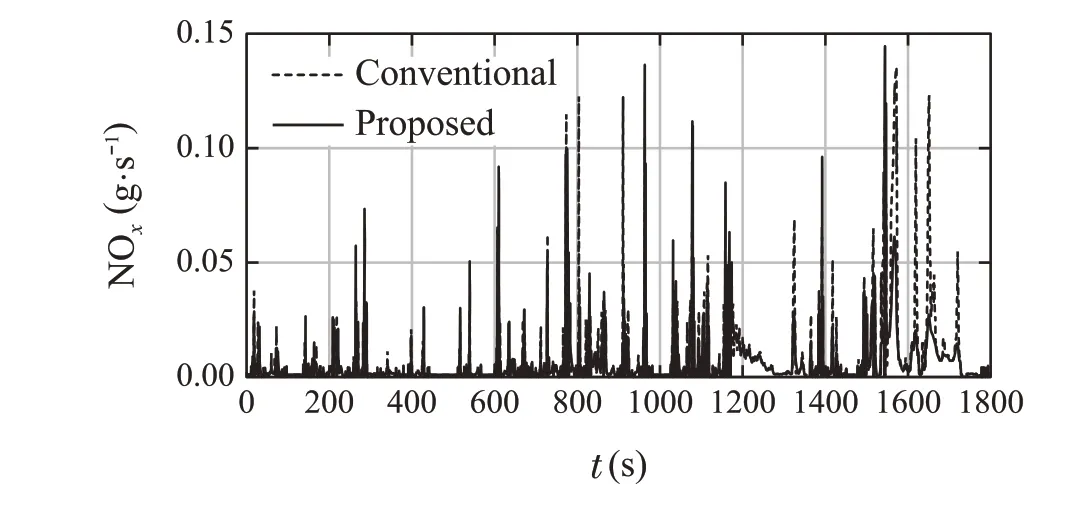
Fig.23 NOx emission

Fig.24 Total NOx emission

This paper addressed the fuel economy optimization problem to improve fuel economy and reduce NOxemissions.First， the fuel consumption and NOxemissions were modeled to capture the characteristics of the engine，and then the battery and motor were modeled.We proposed a hierarchical control method divided into two levels to deal with the problems of different time scales.In the high-level controller，the eco-driving problem that determines the required torque was treated to reduce fuel consumption and NOxemissions by considering tracking to the reference vehicle speed. In the low-level controller， the torque distribution problem determines the distribution between the engine torque and motor torque for the required torque. The evaluation function is designed based on the model characteristics of the engine，battery，and motor.The reference values for fuel consumption and NOxemissions were set based on the illustrated thermal efficiency and NOxemission rate， respectively. Ultimately，the effectiveness of this paper was confirmed using numerical simulation.The simulation results showed that the high load operating points are reduced by the eco-driving problem and that the motor is efficiently assisted at high load operating points where the engine is not efficient by the torque distribution problem.The fuel economy was improved，and NOxemissions were reduced;thus，the effectiveness of this paper could be confirmed.

In future work，it is necessary to consider the heat load of the engine and battery and apply nonlinear control methods to account for the nonlinear characteristics.