Finite-size scaling analysis of the Planck’s quantum-driven integer quantum Hall transition in spin-1/2 kicked rotor model*

ZHANG Jialong， ZHANG Long， ZHANG Fuchun

(Kavli Institute for Theoretical Sciences and CAS Center for Excellence in Topological Quantum Computation, University of Chinese Academy of Sciences，Beijing 100190, China)

Abstract The quantum kicked rotor (QKR) model is a prototypical system in the research of quantum chaos. In a spin-1/2 QKR, tuning the effective Planck parameter realizes a series of transitions between dynamical localization phases, which closely resembles the integer quantum Hall (IQH) effect and the plateau transitions. In this work, we devise and apply the finite-size scaling analysis to the transitions in the spin-1/2 QKR model. We obtain an estimate of the critical exponent at the transition point, ν=2.62(9)， which is consistent with the IQH plateau transition universality class.

Keywords quantum kicked rotor; integer quantum Hall effect; critical phenomena; finite-size scaling

The kicked rotor model describes a particle moving on a circle and is kicked periodically by a space-dependent potential term. It is a prototypical model in the research of both classical and quantum chaos[1-3]. For a sufficiently large kicking strength, the energy of a classical kicked rotor grows linearly with time,E(t)∝t， as a result of the Brownian motion in the momentum space. However, such linear diffusive motion is suppressed in the long-time limit for a quantum kicked rotor (QKR) due to the destructive quantum interference, leading to a dynamical localization in the momentum space[4]. The kicked rotor model has been generalized to higher dimensions and spinful particles[5-12].

A particular interesting discovery is the Planck’s quantum-driven integer quantum Hall (IQH) effect in a spin-1/2 QKR model[13-14], which establishes a surprising bridge between chaotic systems characterized by the sensitivity to initial conditions, and the topologically robust IQH effect with a quantized Chern number. It is analytically shown that, by tuning the effective Planck’s quantumhe, the model defined in Eq. (2) exhibits an infinite number of “Hall plateau” transitions between the dynamically localized insulating phases. Each insulating phase is characterized by an integerσHanalogous to the quantized Hall conductance of IQH plateaus. The critical metallic states at the transition points are predicted to possess a universal “longitudinal conductance”σ*=limt→∞E(t)/t, and belong to the universality class of the IQH plateau transitions. The emergence of these transitions has been observed in numerical simulations[13-14]. However, precise calculations of the critical exponents at the “plateau transitions” have not been achieved, thus leaving the universality class of the transitions not fully confirmed.

In this work, we apply the finite-size scaling analysis to the plateau transitions in the spin-1/2 QKR model. With extensive numerical simulations near the critical point and finite-size scaling analysis, we obtain an estimate of the critical exponent at the critical pointν=2.62(9)， which is consistent with the IQH plateau transition universality class.

1 The model

We shall study the spin-1/2 QKR model introduced in Ref. [15]. A spin-1/2 particle moves on a circle of unit radius and is kicked periodically by a potential field, whose strength depends on the position the particle. Denote the two-component spinor wavefunction by Ψt. Its dynamics is governed by the time-dependent Schrodinger equation,

ihe∂tΨt=H(t)Ψt,

(1)

in which the Hamiltonian is given by

H(t)=H0(p1,p2)+V(θ1,θ2)∑s∈Zδ(t-s),

(2)

whereθ1(modulo 2π) is the angular position of the particle, andp1=ihe∂θ1is the conjugate momentum operator. While the model is defined in two space dimensions, we shall show in Sec. 2.3 that it can be simulated effectively in 1D with the technique of dimension reduction. The canonical commutation relation is given by [θi,pj]=iheδij.The effective Planck’s constantheis a tuning parameter in the model.

The generic form of the potential energy term is given byV=Vi(θ1,θ2)σi， whereσi(i=1, 2, 3) are the Pauli matrices. The Einstein summation convention is used. The potential energy term couples the spin and the angular position of the particle,

V(θ1,θ2)=(2arctan(2d)/d)d·σ,

(3)

with the vectordgiven by

d=(sinθ1,sinθ2,0.8(μ-cosθ1-cosθ2)).

(4)

This potential term of the spin-1/2 QKR model was first introduced in Ref. [15], which was inspired by the Qi-Wu-Zhang model of quantum anomalous Hall effect[16]. A series of phase transitions driven by the effective Planck parameterhewas found in Refs. [13-14], which resembles the IQH plateau transitions in various significant aspects.

In this work, we shall focus on the latter case and fixμ=1 in the rest of this work.

1.1 Floquet operator

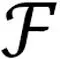
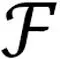
(5)

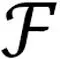
Ψq(θ)=eiq·θu(θ),

(6)

whereq=(q1,q2) with the constantsq1,2∈(0,1)， andu(θ) is a 2π-periodic function of the angle variablesθ.Therefore, for these eigenstates,H0(-ihe∂θ) can be replaced byH0(-ihe∂θ+heq) acting onu(θ).The corresponding Floquet operator reads

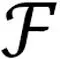
(7)

1.2 Mapping to the Anderson model

The QKR model can be mapped to the Anderson model of a particle moving in a quasi-disordered system, signifying the link between quantum chaos and Anderson localization[4,17]. Let us first omit the spin degree of freedom and define the eigenstate of the Floquet operator by

(8)

in whichεis called the quasi-energy. Here |a+〉 is the eigenstate of the Floquet operator immediately after the kick. Define

|a-〉=eiV|a+〉=e|a+〉,

(9)

which is the eigenstate before the kick, then |a±〉 satisfy

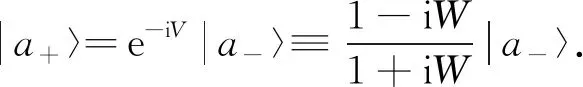
(10)

|a+〉=(1-iW)|u〉,

(11)

|a-〉=(1+iW)|u〉.

(12)

Substituting into Eq. (9), we find |u〉 satisfies the following secular equation,

(13)

In the momentum space with a basis {|n〉}， wherep|n〉=hen|n〉， and with the spin indices recovered, we arrived at

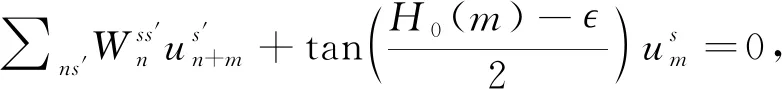
(14)

(15)

Wis diagonal in the angular position representation. Given the form ofVin Eq. (3), we find

W=2d·σ.

(16)

1.3 Dimension reduction

The 2 D QKR model can be effectively reduced to 1D by choosing an incommensurate driving frequency in the second dimension[5-6,18]. Consider the following separable kinetic energy term,

H0(p1,p2)=H0(p1)+ωp2,

(17)

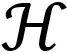
(18)

and the transformed Hamiltonian is given by

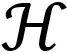
H0(p1)+V(θ1,θ2+ωt)∑s∈Zδ(t-s),

(19)

where the translation relation eiωp2t/heV(θ2)e-iωp2t/he=V(θ2+ωt) is used. The Schrodinger equation in the interaction picture reads

ihe∂tΨI=HIΨI,

(20)

in which the Hamiltonian is given by

HI=H0(p1)+V(θ1,θ2+ωt)∑s∈Zδ(t-s).

(21)

This is a 1D model, which dramatically simplifies the following numerical calculations. The corresponding Floquet operator is given by

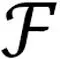
(22)

wheren1=p1/he.In the following numerical simulations, we adopt the kinetic term

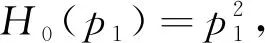
(23)

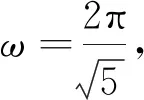
2 Numerical simulations

We work in the momentum representation in numerical simulations. The Hilbert space is truncated to be 2N-dimensional such that the momentum indexn∈[-N,N-1].Two types of initial states are considered in our simulations. The first one is of theδ-function form,

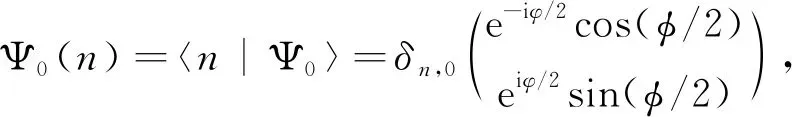
(24)

while the second is a Gaussian wave-packet given by

(25)

up to a normalization factor. We choosen0=0 and several differentσin our simulations and find that the diffusion rates defined below in the late-time dynamics are not sensitive to the choice of initial states. Below we show results obtained with the initial states of theδ-function.

The diffusion rate is defined by

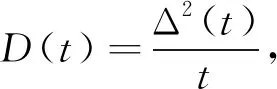
(26)

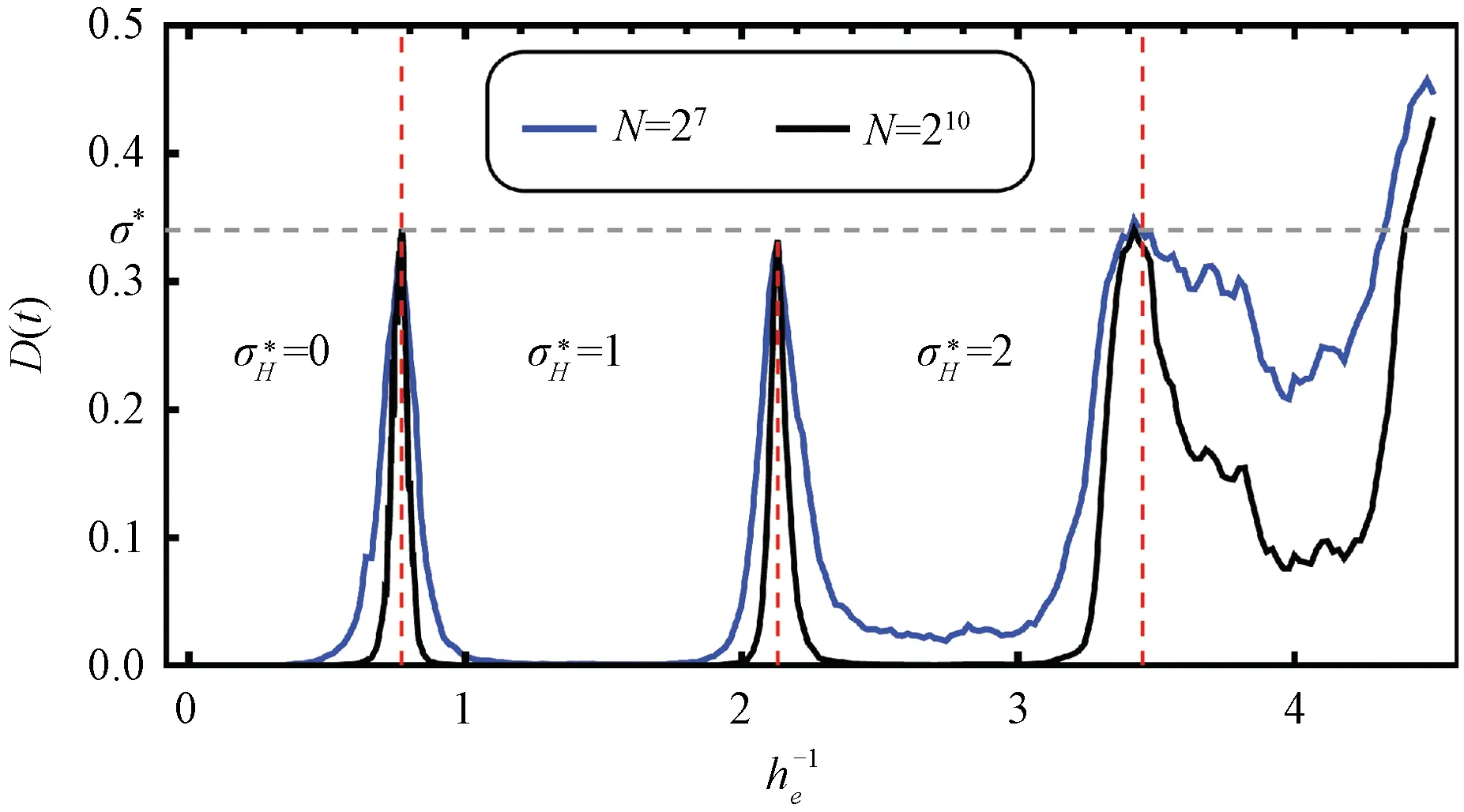
We take ensemble average over 400 different values of α∈(0,2π) and q∈(0, 1). We set t=N2/4. The transitions occur near and 3.45 as indicated with red dashed lines. The diffusion rates converge to a universal value σ*≃0.33 (gray dashed line) at these critical points.

Finite size scaling analysis

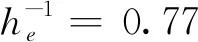
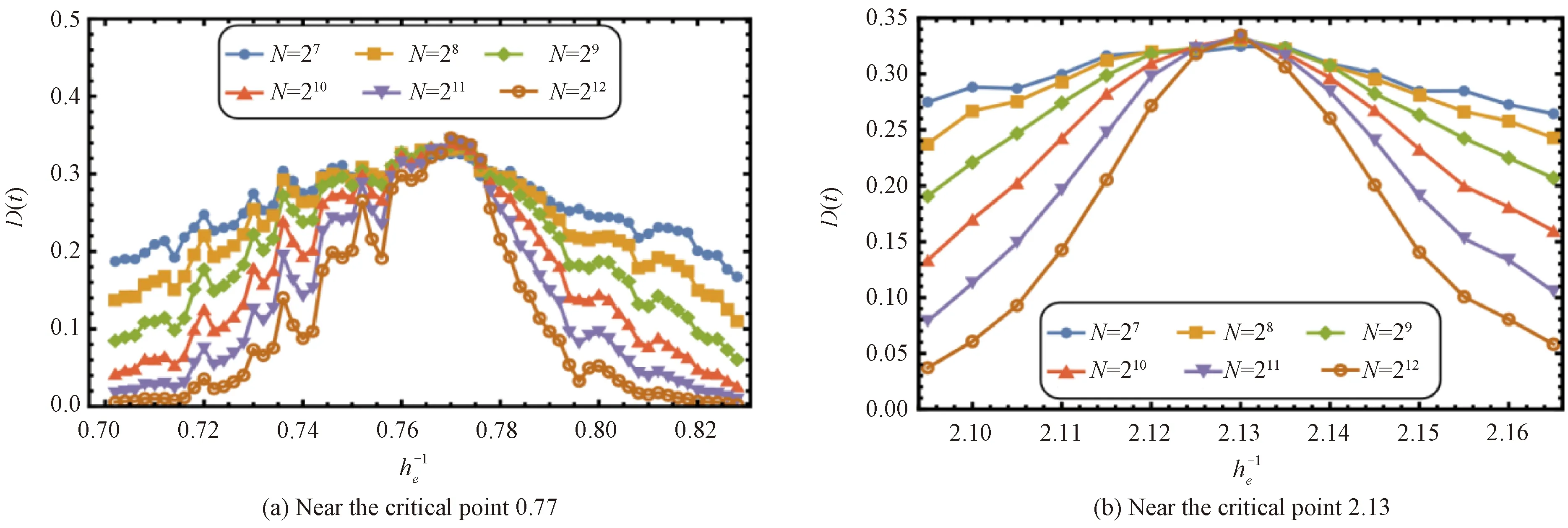
Fig.2 Long-time diffusion rate of the QKR model as a function of near the critical point (a) 0.77 and (b) 2.13 for various N (We set t=N2/4) values

In the long-time limit, the diffusion rateD(t) goes to zero for an insulating state with dynamical localization in the momentum space, and approaches a nonzero value for a metallic state. According to the scaling theory of Anderson localization, the diffusion rate obeys the one-parameter scaling law. Near the critical point, the diffusion rate has the scaling form,

D(h,t)=ξ2-dF(ξ-dt).

(27)

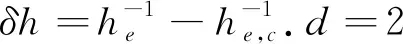
D(h,t,N)=f(t/N2,hN1/ν)≡f(x,y),

(28)

withx=t/N2， andy=hN1/ν.fis a non-singular function of its arguments. In the simulations, we chooset=N2/4， thusx=1/4 is fixed, and expandfinto the power series ofy,

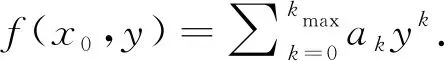
(29)

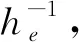
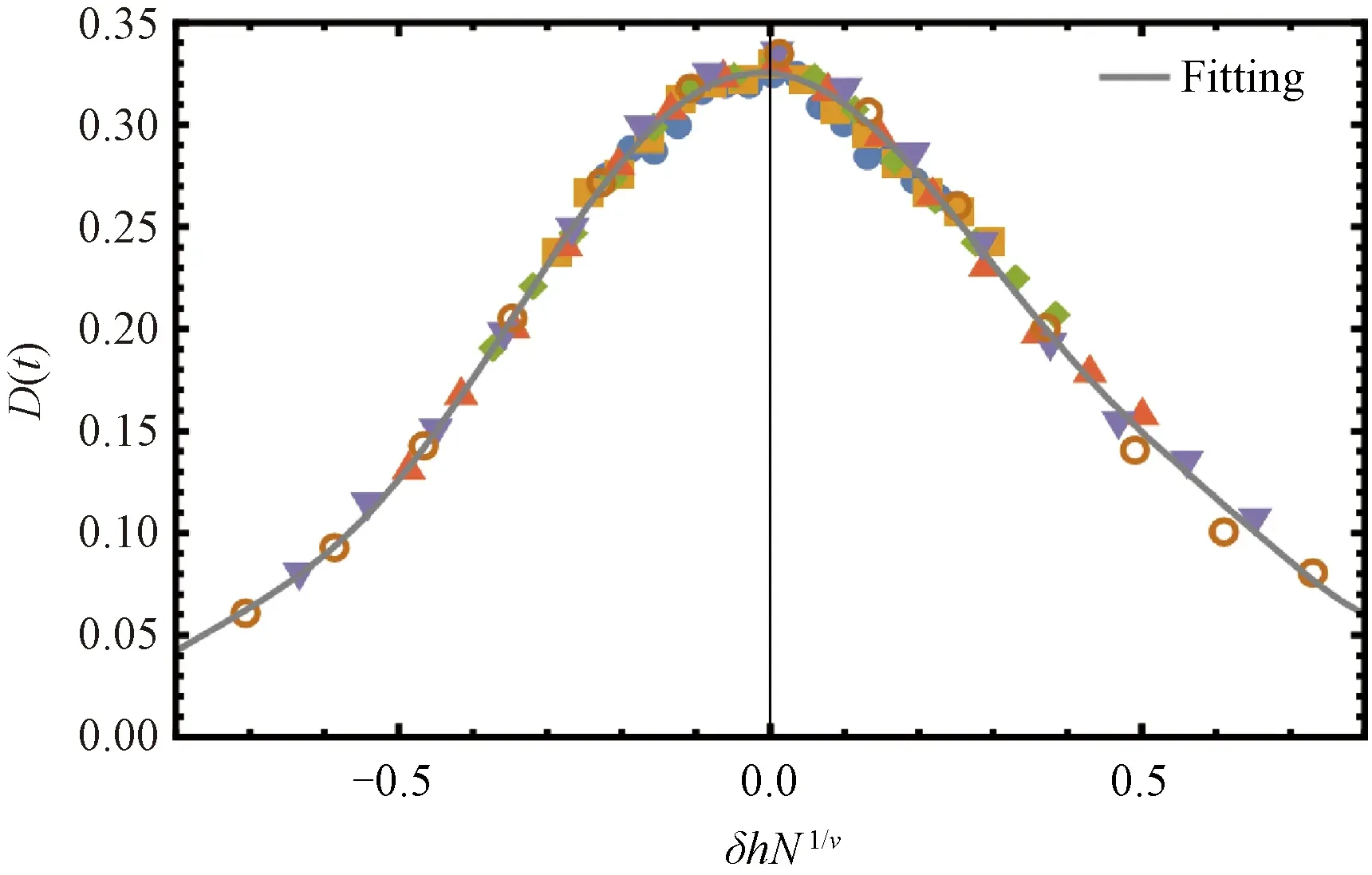
Fig.3 Data collapse of the diffusion rate D(t) in Fig.2(b) according to finite size scaling form in Eq.(28)

3 Conclusion

To summarize, we have studied the spin-1/2 QKR model with extensive numerical simulations. By devising and applying the finite-size scaling analysis near the critical point between different dynamical localization phases, we obtain the numerical estimate of the critical exponentνand the universal diffusion rateσ*at the critical point. We confirm that the transition belongs to the universality class of the IQH plateau transition.