基于北斗系统的桥梁高精度监测算法研究

包龙生，陶天阳，于玲*，冯乃辉

(1.沈阳建筑大学交通工程学院， 辽宁沈阳110168；2.鞍山市城市建设发展中心， 辽宁鞍山114002)

0 引言

由于大型桥梁施工难度大，设计结构复杂多样，因此在桥梁施工和运营过程中会受到各种作用的影响。在这些作用的影响下，桥梁结构将发生变形。只有在一定的时间间隔内检查变形，才能防止损坏桥梁，避免重大灾害和事故[1]。

为了防止这些灾害，监测桥梁非常重要[2]。1997年，阿什肯扎伊等人首次使用GPS监测英国亨伯大桥的变形。尽管当时测量结果不够准确，但这是通过卫星监测监测桥梁变形的一个里程碑[3]；2000年，Fujino利用GPS对石明海峡大桥的变形进行了测量和监测。为了分析桥梁整体变形，比较和分析了温度、风速和其他因素的影响[4]；2012年，中国交通部公路研究院首次将北斗系统应用于广东省珠江黄埔大桥的监测。本次试验中，监测点分别设置在北桥和南桥索塔上，参考站设置在桥梁管理处，共同组成桥梁应变监测系统，实时监测桥梁变形[5]。

本文采用快速准确地确定载波相位信号整数模糊度的方法，使用LAMBDA算法解决北斗系统的模糊度，检测和修复可能出现的周跳现象，并提出改进的TurboEdit方法，提高北斗系统的测量精度。最后，以一座大跨度斜拉桥北斗变形监测系统为例，对采集的数据进行误差处理，并将测量精度与《中国北斗系统监测精度规范》进行验证，验证本文的误差处理方法能否实现厘米级误差测量，满足桥梁变形监测的要求远程桥梁[6]。

1 整周模糊度的解算

1.1 整周模糊度解算

北斗监测系统中最常用的是B1波段信号。在B1波段信号中，最高频率载波信号为1 575.42 MHz。从北斗系统的观测模型可以看出，当使用北斗系统进行测量时，使用矢量信号的双波相位差观测模型可以减少接收卫星信号传输过程中各种误差的干扰。当地面接收器U和V接收到来自卫星i和j的信号时就有[7]：

(1)

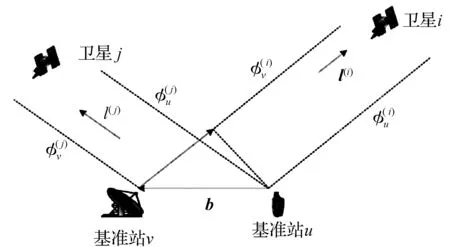
图1 载波相位测量几何关系Fig.1 Carrier Phase Measurement Geometry

载波相位测量几何关系如图1所示，如果参考站和卫星之间的方向向量为l，监测站和参考站之间的矢量为b，因此

(2)

在时间t，当参考站和监测站测得的卫星数为n+1时，所有观测结果中将有n个独立的双差观测，其中一个可以作为参考，形成n组载波相位方程，

Pt=Atb+N+εt,

(3)

式中：Pt为时间t的承重相位向量组，其N阶协方差矩阵为Q0；At是阶数系数K3的矩阵；b是基本载体；N是由整周模糊度组成的n维向量；εt是由噪声误差构成的n维矢量。

当参考站和监测站根据上述公式连续测量m个周期时，可从公式(2)、(3)中获得一般观测方程

P=Ab+BN+ε,

(4)

式中：P是观测值的Mn×1维向量，其协方差矩阵为Q=Im×Q0；A是位置系数的Mn×3维向量；B是整周模糊度系数的Mn×n维向量；ε是接收机噪声误差的Mn×1维向量。

1.2 北斗系统整周模糊度的获取

本文使用快速算法来获得模糊度。这个算法应用了数理统计和假设检查的原理。在求解模糊解之前进行数学分析，早期去除模糊和不合理结果的组合，使下一个计算过程更简单和更有效。具体步骤是使用从初始解和测量方程获得的已知误差来确定可能的模糊的实际范围，并且选择模糊的标准偏差最小的解，即模糊的全局解的集合[8-11]。它可以表示为

(5)

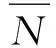
1.3 LAMBDA算法

在分析位置、解释参考向量B和参考站与监测站之间载波相位信号的n个模糊周期总数时，应使用最小平方法估计(5)的最小目标函数

(6)

它可以用来解决最小平方估计实数解的最优值问题。公式(6)可细分为

(7)

当使用最小平方法求解B和N时，可以首先忽略整周模糊度的解必须是一个整数的约束。假设已经知道N范围，可以按如下方式替换公式(8)：

P-BN=Ab+ε。

(8)

此时，表达式等于所需的未知参数。使用表达式(9)，可通过以下方式获得参考站和监测站之间的参考向量B：

(9)

这时再把N当做未知数把已求得的b带入式(7)求出最小值：

(10)

(11)

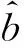
(12)

(13)

在求解全环模糊度参数时，用该参数得到的结果比用浮点解得到的结果更准确。当卫星用于实时动态定位时，2个参数的结果不一致。在用上述方法获得全周模糊度解范围和协方差矩阵后，用最小平方法计算载波相位全周模糊度的过程包括重复求解方程以获得所有解的最小值。得到的最小值是整周模糊度的解N，目标函数方程如下：

(14)

协方差矩阵不一定是对角矩阵，因此使用较少的平方来求解最小值会很慢。此时，LAMBDA算法可用于实现任何模糊度的解算速度。LAMBDA算法使用最小二乘平差法寻找最小模糊度(I=i-1，i-2，…，1)。使用浮点解释最小值，并在搜索过程中按N1到Nn的顺序解释它。因为整数的模糊度是相关的，所以N1和Ni-1之间的值是已知的。如果已知X，则在估计Y的值时，估计值的平均值为

(15)

整周模糊度的目标函数为

(16)

在LAMBDA算法中，离散搜索法用于计算整数的最小模糊度，序贯最小二乘估计法是基于搜索整数的改进最小二乘法。

2 周跳现象的探测与修复

周跳主要原因有很多：首先是阻塞建筑物导致无线信号在载波相位信号传播过程中中断；其次是电离层信号或多径干扰导致信号接收失败；最后是接收机自身的原因，导致数据处理失败。由于循环周跳的发生，信号断点前后的模糊值不一致，因此无法指定确切位置。周期性跳变的发生将影响后续数据量，并不断累积偏差[12-14]。

2.1 对宽巷组合改进

在TurboEdit算法中，该算法过程本质上是一个衰减宽车道模糊和过滤噪声的过程[15-16]。就在卫星能够观测到视点之前,当卫星观测速度不快时,卫星与地面的夹角小,观测结果比较差。在没有这种噪声干扰的情况下，两端的数据不符合模糊度变化规律，因此无法辨别结果根的平均平方是否较大，以及是否在中间部分出现周跳现象。如果中段的数据质量相对较好，结果平均值能较好地反映模糊性的变化规律，相应的根的平均平方也就相对较小，这主要是通过在两端不稳定波形中加入中间段的数据来检测周跳。如果计算结果远小于实际值，可能出现周跳检测误差，测量结果不准确[17-20]。所以移动平均法可以有效解决这些问题，即取n个连续数据作为模糊度全长所有数据的每个数据的距离加权平均值：

(17)

①由于当卫星刚刚看到的视点与地面之间的角度在30°之间时，由多径误差和对流层误差测量的数据不准确，因此平滑运动的步长被定义为历元数。也就是说，S1=i，S1是步长，i是历元的值；

②如果卫星运行与地面之间的角度大于30°，则多径效应引起的误差与对流层引起的误差相对平衡，平滑运动设置为S2=min(n/1 025)。其中n是角落中的纪元数；当卫星离开观测点时，卫星与地面的夹角逐渐小于30°，平滑运动节距增大，与地面成30°的平滑运动距离也减小。平滑运动距离的设置与数据的采样率相关。如果数据采样率为30 s，i=100，卫星与地面之间的角度为30°，平滑移动步长为S3=100-(Sine)，e为反向远点与地面之间的角度。

其中S1=i，i是当前日历值。S2=min(n/1 025)，n是弧段中的历元数。S3=100-(Sine)，e是当前历元的卫星角度。最后，将等式(17)引入真实周跳值，以判断是否发生周跳。

2.2 对电离层残差组合进行改进

电离层组合用于计算2个相邻能源之间载波相位信号的差异，并避免伪距电离层残余的组合，

ΔLJi=λ1Δd1-λ2Δd2。

(18)

3 案例验证及结果分析

3.1 案例简介

本文以太文高速温州段飞云江大桥为例。飞云河大桥起链为(K313526～K317515)，全长3 989 m，其中非航空引桥为预应力混凝土等截面箱梁50、45、(30+40+30)m连续梁。通航部分范围为(50+110+380+110+50)m双塔扁索组合梁斜拉桥。下部结构采用墙墩和钻孔桩。主教塔是“A”型塔身。底座主盖采用哑铃盖，副坞、过渡坞采用整体盖。囊性纤维变性。北斗监测精度规格见表1。表1中精度数值为1倍中误差，定位精度为在CGCS2000坐标系中的精度；可用性指标为不顾及通信网络可用性条件下的指标。

表1 系统技术参数Tab.1 System technical parameter table

3.2 数据验证分析

桥塔位移测点位于桥塔顶部，基点设在2 km以内的稳定基础上。有1个基点和3个测量点。具有已知坐标的固定基站被定义为参考点，桥塔上的监测点被定义为测试点。同时对参考点和测试点进行监测，分析监测数据的误差。保持同一颗卫星长时间监测监测点，以确保数据分析的准确性。桥梁模型如图2所示，桥塔GNSS测点布置如图3所示。

图2 全桥模型图Fig.2 Layout of the measuring points

图3 桥塔GNSS测点布设示意图Fig.3 Schematic diagram of GNSS measuring point arrangement of bridge tower

本文采用C语言开发的跨平台集合中的GAMP软件，结合了服务器和客户端的解释功能。它是一个开源的GNSS分析软件，可用于精确的多星座和多频率定位。该软件可以基于差分和非组合观测准确检测多个GNSS。虽然Gamma是基于RTKLIB的二次开发，但是有很多改进，例如周期性滑动检测、接收机时钟跳跃恢复、伪Gamma频率偏移处理等。目前，GAMP扩展到高精度实时定位软件，具有实时估计多星座和多频率相位偏差，模糊PPP固定，对流层和电离层网格建模，PPP，RTK等功能。GAMP输出文件是简单统一的格式，包括定位结果、卫星数量、卫星高度、伪距离和剩余载波相位、全电子梯度等以获取解析结果。

3.3 数据预处理

通过RTKplot模块，以图形方式显示卫星能见度、天视、DOP精度系数、信噪比、多径效应、卫星仰角等情况。从图4—7可以看出，卫星数据分布均匀，卫星轨道运行良好，卫星能见度良好，DOP精度系数一般较小，多径效应接近0。

图4 可见卫星图标Fig.4 Visible satellite icon

图5 卫星天空试图Fig.5 Satellite sky attempt

图6 精度因子DOPFig.6 Precision factor DOP

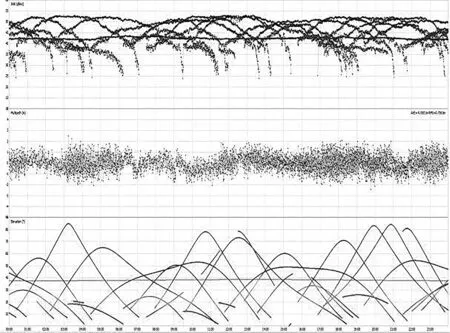
图7 载噪比、多路径效应、卫星高度角图Fig.7 Signal-to-noise ratio, multipath effect,satellite altitude angle map

3.4 北斗系统测量结果

图8至图17为各站点基于北斗系统使用软件按上述解算方案景进行解算的E、N、U三个方向上的收敛曲线图。从图8至图17的收敛图中可以看出,每个站点的方向的误差值随着时间推移而变化,但总体差值呈下降趋势。从收敛时间的角度来看,每组数据基上可在方向的U误差平均值为0.08 m,北斗精密单点定位技术可以实现误差厘米统量,基本满足大跨度桥梁变形监测要求。

图8 Wtzz站收敛曲线图Fig.8 Wtzz station convergence curve

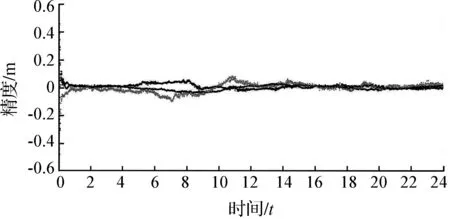
图9 Spt0站收敛曲线图Fig.9 Spt0 station convergence curve

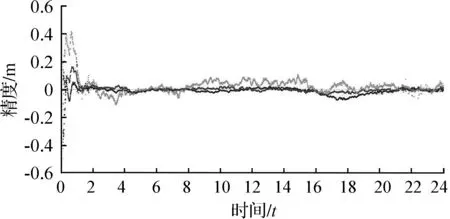
图10 Muge站收敛曲线图Fig.11 Muge station convergence curve

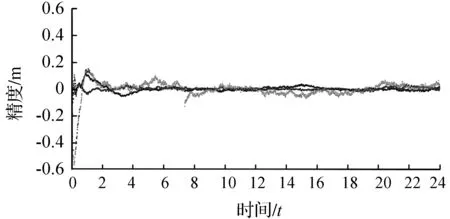
图11 Kokv站收敛曲线图Fig.10 Kokv station convergence curve

图12 Hrao站收敛曲线图Fig.12 Hrao station convergence curve

图13 Gop6站收敛曲线图Fig.13 Gop6 station convergence curve

图14 Hers站收敛曲线图Fig.14 Hers station convergence curve

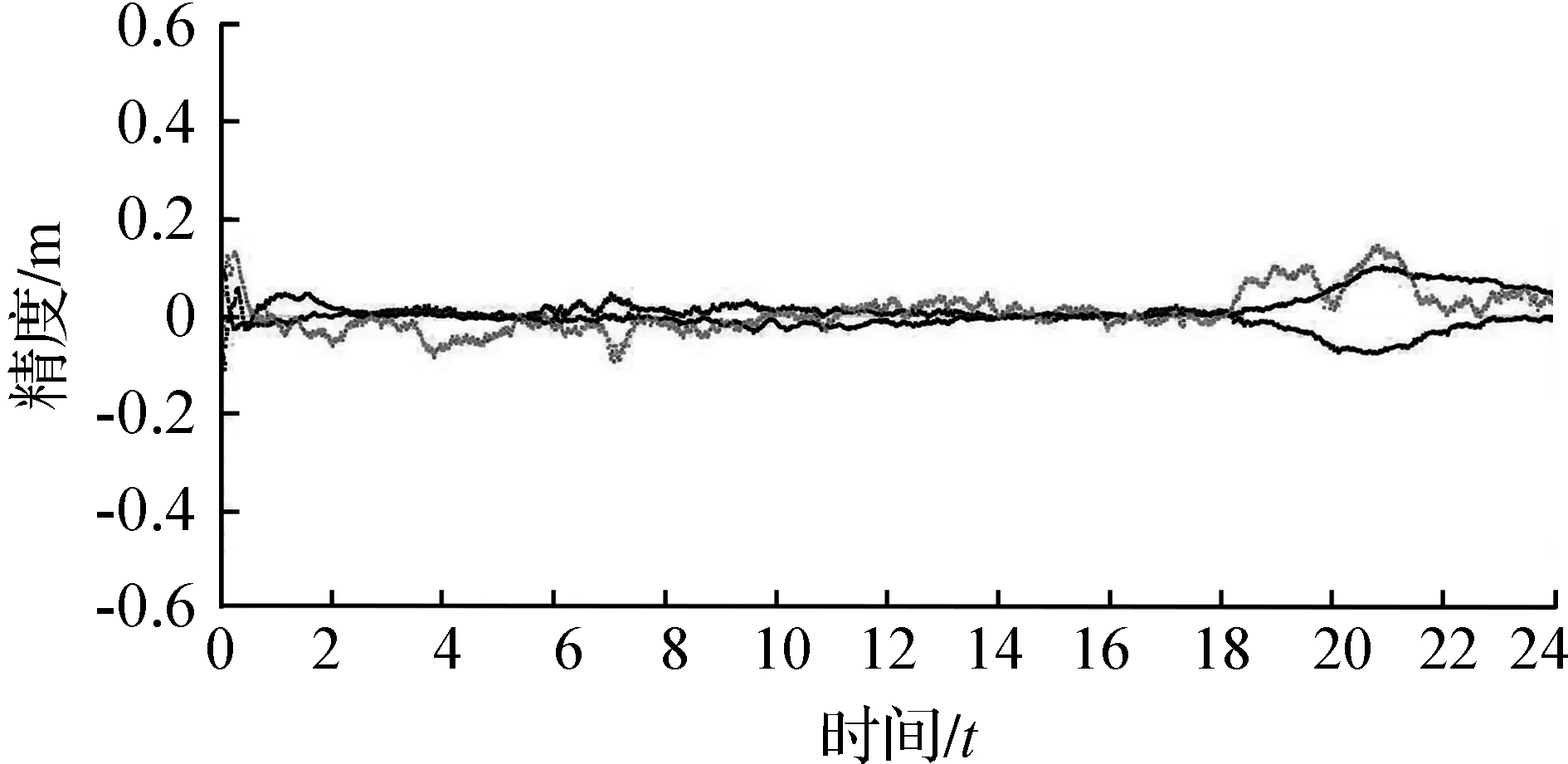
图15 Gode站收敛曲线图Fig.15 Gode station convergence curve

图16 Cebr站收敛曲线图Fig.16 Cebr station convergence curve

图17 Brew站收敛曲线图Fig.17 Brew station convergence curve

表2 监测站点在不同方向的误差值Tab.2 Error values of monitoring stations in different directions

4 结论

本文主要研究基于北斗系统的大跨度桥梁变形监测。将北斗系统高精度定位技术应用于大跨径桥梁变形监测，包括桥梁变形机理、北斗系统定位算法的建立和定位误差修正。具体结论如下：

①从桥梁变形原理出发，改进了北斗定位系统的功能模型和误差模型。

②重点研究了整周模糊度的求解方法和周跳检测与恢复算法。LAMBDA算法用于在搜索最小整数时纠正歧义并改进最小整数的顺序估计。提出了一种主动检测和恢复算法来改进TurboEdit法，并提出了一种移动平均法，用于在宽车道和窄车道混乱的情况下对每个站点前面的平均测量结果进行检测。对于电离层剩余组合，改进电离层组合计算相邻2个能量源之间载波相位信号差法，避免电离层误差。

③考虑误差修正和其他参数的北斗系统位置解算。从单点精密定位结果的收敛图可以看出，U方向各站的误差值大于其他2个方向的误差值，然而，从变化趋势来看，U方向的误差值呈下降趋势。就收敛时间而言，每组数据基本在2 h内收敛。BDS中大多数站点的误差值在10 cm以内，其中E方向上的平均位置误差值为0.04 m，N方向的平均位置误差值为0.08 m，U方向的平均位置误差值为0.08 m。北斗精密单点定位技术可实现厘米级误差测量，满足桥梁变形监测的要求。