双向地震作用下型钢混凝土框架两阶段Pushover分析
2022-07-06王朋丁耀宗史庆轩1李龙堂
王朋,丁耀宗,史庆轩1,,3,李龙堂
(1.西部绿色建筑国家重点实验室, 陕西西安710005;2.西安建筑科技大学土木工程学院, 陕西西安710005;3.结构工程与抗震教育部重点实验室, 陕西西安710005)
0 引言
随着基于性能抗震设计方法的广泛应用,静力弹塑性分析方法(Pushover方法)越来越受到人们的重视[1-2]。Pushover方法具有良好的工程实用性,能以较少的时间求出结构的薄弱部位并达到工程所需要的变形验算精度。传统的Pushover方法是将结构等效为单自由度体系推覆至预定目标位移进行分析,该方法只考虑一阶振型,对受高阶振型影响较大结构的计算结果有较大误差[3]。为解决该问题,振型Pushover分析方法应运而生[4-7],称为MPA方法。MPA方法最早由Chopra等[4]提出,将结构需要考虑的各个振型分别进行Pushover分析,然后将各自的地震作用效应按照一定方式进行组合得到结构的最终响应。随后,Tysh等[8]、刘青山等[9]和毛建猛等[10]对MPA方法进行了改进,减小了MPA方法计算难度,但振型Pushover方法中多自由度体系结构各振型的侧移变形只符合各自振型下的地震响应,组合之后仍与结构自身侧移变形有误差[11]。与此同时,Pushover分析多集中于钢筋混凝土框架的研究[12-13],型钢混凝土框架(steel reinforced concrete, SRC)研究较少,史庆轩等[14]对型钢混凝土框架结构进行推覆分析,提出了SRC结构基于位移的抗震设计方法;楚留声等[15]运用Pushover方法分析了SRC结构的抗震性能;薛建阳等[16]运用Pushover方法对型钢混凝土异形柱框架进行了弹塑性分析。由于SRC结构研究多为单向地震作用下的研究,而实际地震中结构受到双向地震作用,其损害程度大于单向地震[17],因此有必要对型钢混凝土框架结构进行双向地震作用研究。
为提高Pushover方法的计算精度,弥补双向地震作用下型钢混凝土框架Pushover分析研究的不足,本文建立了双向地震作用下型钢混凝土框架的两阶段Pushover分析方法,称为CMPA方法,即将各振型组合得到的结构位移归一化处理后作为推覆侧移向量对结构进行第二次Pushover分析,得到的地震作用效应即为结构最终的地震响应。并采用多种Pushover方法对型钢混凝土框架结构进行比较分析,结果表明,两阶段Pushover方法计算双向地震作用下型钢混凝土框架的结构响应有较好的精度。之后通过探究Pushover中塑性铰的出现过程对型钢混凝土框架进行分析,证明型钢混凝土框架也可实现“强柱弱梁”的结构模式,具有较好的抗震性能。
1 基本原理
1.1 考虑多振型的Pushover方法
将原结构多自由度体系转化为等效单自由度体系,为此假定:①多自由度体系按照假定的侧移形状产生地震反应;②2种体系的基底剪力相等;③地震作用在2种体系上所做的功相等。
设多自由度体系i质点的质量为mi,水平力为Fi;第j振型下等效单自由度体系的等效质量为Mjeff,等效刚度为Kjeff,等效位移为ujeff,等效加速度为ajeff,基底剪力为Vbj,多自由度体系向等效单自由度体系的转化如图1所示。

图1 多自由度体系向等效单自由度体系的转化Fig.1 Transition from multi-degree freedom system into equivalent single-degree freedom system
由于多自由度体系第j振型各质点加速度aji与uji成正比,因此
(1)
根据假定②基底剪力相等可知
(2)
可得原结构各质点的水平地震作用为
(3)
则单自由度体系的等效位移为
(4)
将第j振型结构各质点位移用位移形状向量和结构顶点位移ujr表示,则
uji=φjiujr,
(5)
(6)
式中:φji为第j振型i质点的振型值;γj为第j振型的振型参与系数。则已知等效单自由度体系的等效位移ujeff,相应原多自由度体系各振型的顶点位移可知
ujr=γjujeff。
(7)
1.2 求解SRC结构目标位移
本文采用能力谱法求解SRC结构目标位移,具体步骤如下:
①在结构上施加静力荷载,按第j振型的水平分布力Fj对结构进行Pushover分析,得到第j振型的基底剪力-顶点位移(Vbj-ujr)推覆曲线,并简化为双线型模型。其中Fj的计算公式为
Fj=Mφj,
(8)
式中:M为结构质量矩阵;φj为第j振型的振型向量。
②建立能力谱曲线。在第j振型的地震过程中,结构沿高度的侧移用一个不变的形状向量φj表示,这样将原结构等效为一个单自由度体系,而Vbj-ujr推覆曲线逐点转化为等效自由度体系的谱加速度-谱位移(ADRS格式)曲线,即
(9)

③采用规范加速度反应谱(Sa-T谱)建立需求谱曲线。我国规范的设计反应谱为地震影响系数(α-T)曲线,需转化为特定的SRC结构的Sa-T谱曲线,RC结构弹性阻尼比ζ0取0.05,钢结构取0.02,由于SRC结构的性能介于RC结构和钢结构之间,因此本文对其取为0.04[14],则计算公式为
(10)
式中:αmax为地震影响系数最大值;Tg为场地特征周期;T为结构自振周期。
1.3 CMPA方法
将第一阶段的推覆结果通过式(7)求得多自由度体系各振型下顶点位移,则通过下式可得第j振型的结构位移uj,
uj=φjujr。
(11)
将x方向各振型的结构位移进行组合可得多自由度体系x方向位移ux
(12)
且ux中的顶点位移为urx。
将ux进行归一化处理并作为侧移向量对型钢-混凝土框架结构进行第二次Pushover分析,推覆至目标位移urx,进行x方向弹塑性过程分析,得到的楼层侧移为uxc。
同理可得多自由度体系y方向位移uy及ury,并采用上述相同的方法沿y方向对型钢-混凝土框架结构进行第二次Pushover分析,推覆至目标位移ury,进行y方向弹塑性过程分析,得到的楼层侧移为uyc。
1.4 双向地震作用下的Pushover
双向地震作用下结构受到的损害比单向地震作用下更为严重,有必要对结构进行双向地震作用下的研究,但Pushover方法是单向推覆,因此本文对结构进行2个方向地震作用效应组合来达到双向地震作用效应。
考虑双向地震作用效应组合的方法有2种:①采用某一方向地震作用效应的100%加上另一方向地震作用效应的30%;②对2个方向地震作用效应采用SRSS组合,且认为2个方向的反应谱是相同的。本文采用第二种方法,它是根据随机振动理论推出的,具有统计性质的含义,得出的结果与实际反应也最接近。
设x方向下地震作用效应为Ax,y方向下地震作用效应为Ay,按照SRSS方法进行组合,
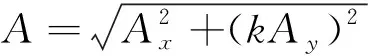
(13)
式中:A为双向地震作用下地震作用效应的组合值,取其计算最大值,本文选取楼层侧移值作为地震作用效应;按照我国建筑抗震设计规范,k取0.85。
将CMPA方法推覆得到的uxc和uyc代入式(13)得

(14)
式中u为双向地震作用下型钢混凝土框架两阶段Pushover分析方法得到的楼层侧移。
2 双向地震作用下两阶段Pushover分析步骤
①根据建筑结构的使用功能、建筑类别、抗震等级等进行型钢混凝土框架结构的初步设计,主要包括确定结构层高、柱网尺寸、材料强度等级以及构件截面尺寸等。
②计算结构各振型向量φj与模态频率ωj并对振型向量作归一化处理;计算各楼层重力荷载代表值Gi及各项内力。

④建立能力谱曲线与需求谱曲线,并转化为ADRS格式。
⑤将能力谱曲线与需求谱曲线绘制在同一张图中,得交点为等效单自由度体系的等效位移ujeff,采用式(7)转化为结构顶点位移ujr,代入式(11)可得第j振型的楼层侧移uj。
⑥重复步骤④、⑤确定前m个振型的楼层侧移,将各个振型计算所得的楼层侧移采用式(12)进行组合,求得多自由度体系楼层侧移ua。
⑦利用步骤⑥得到的楼层侧移ua归一化处理后对型钢-混凝土框架结构进行推覆,进行第二次Pushover分析,得到x方向和y方向的楼层侧移uxc和uyc。
⑧将得到uxc和uyc通过式(14)组合得到双向地震作用下型钢混凝土框架的楼层侧移u。
3 算例
3.1 算例介绍
本文采用的SRC结构算例为8层结构,层高均为3.3 m,混凝土强度等级为C30,型钢采用Q345热轧钢,钢筋直径14 mm的HRB400级钢筋。结构平面布置如图2所示,x方向为纵向,y方向为横向,柱1—8为边柱,其余柱为中柱,梁柱截面尺寸见表1,型钢截面尺寸见表2。采用SAP2000结构分析软件对其进行计算分析,该场地抗震设防烈度为8度,多遇地震加速度为0.16 g,罕遇地震加速度为0.9 g,设计地震分组为第一组,场地类别为Ⅱ类。

图2 SRC结构平面布置Fig.2 Structural layout plan of SRC

表1 梁柱截面尺寸Tab.1 Section dimensions of beam and column mm×mm

表2 型钢截面尺寸
3.2 建模过程
首先对结构进行模态分析,确定参与振型,经计算选用y方向振型为1、4、7阶振型,x方向振型为2、5、8阶振型进行振型Pushover分析,参与振型的等效单自由度体系参数见表3。

表3 等效单自由度体系参数Tab.3 Parameter of equivalent single degree of freedom system
Pushover分析中,对梁单元,仅考虑弯矩产生的塑性铰,对柱单元,需要考虑由轴力和双向弯矩共同作用产生的塑性铰,因此梁采用M塑性铰设置,柱采用P-M-M塑性铰设置。将结构进行单向推覆,各振型得到的Pushover结果通过能力谱法得到各振型下的目标位移及位移向量uj,之后通过式(12)组合后进行第2次Pushover分析。
本文通过时程分析得到的地震作用效应作为精确值来校验Pushover方法的准确性,将地震波双向输入,由于结构y方向抗侧力较小,为受地震影响较严重一侧,将y方向地震波完整输入,x方向地震波取0.85倍输入。地震波分别选ELECNTRO波、兰州波、唐山波作进行计算,3种地震波下结构的地震作用效应平均值即为结构受双向地震作用下的精确值。
3.3 算例结果
传统的一阶推覆、MPA方法、本文的CMPA方法以及时程分析方法的结构变形分别如图3、4所示。从中可见,本文的CMPA方法计算型钢混凝土结构在双向地震作用下的误差更小。双向地震作用下型钢混凝土结构Pushover分析方法对比结果见表4。

(a) x方向楼层侧移

(c) 双向楼层侧移

(e) y方向层间位移
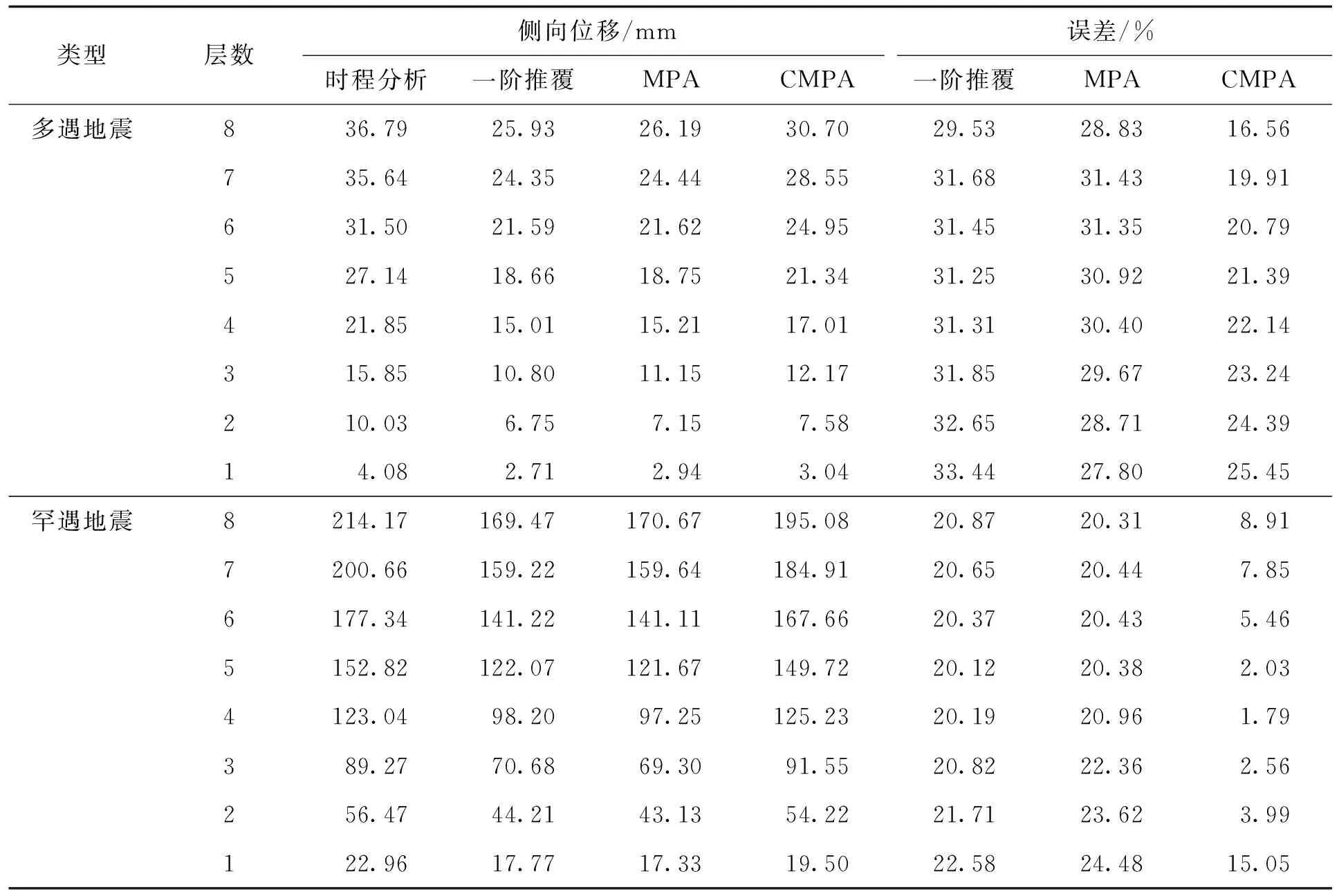
表4 双向地震作用下型钢混凝土框架Pushover分析方法对比Tab.4 Comparison of Pushover analysis methods for steel concrete frame under bidirectional earthquake actions
由图3可知,x、y方向以及双向地震作用下,MPA方法的计算结果与仅考虑一阶振型的传统Pushover方法计算结果相近,但与时程分析结果并不相近,表明多遇地震下SRC结构使用MPA方法提升效果不显著。这是由于多遇地震下结构所受到的地震作用主要由低阶振型控制,高阶振型对结构的影响较小,因此MPA方法中高阶振型的影响在此不能体现。x、y方向以及双向地震作用下CMPA方法计算结果的精确度相对于MPA方法有所提升,楼层侧移与层间位移结果均较接近时程分析结果,表明两阶段Pushover方法可以适用于多遇地震下SRC结构。
罕遇地震下结构变形如图4所示,x、y方向以及双向地震作用下,MPA方法的计算结果与仅考虑一阶振型的传统Pushover方法计算结果相近,这是由于框架结构层数较低时地震作用主要由低阶振型控制,受高阶振型影响较小,MPA方法在高阶振型的优势不能很好体现,因此使用MPA方法提升效果并不显著。x、y方向以及双向地震作用下CMPA方法计算结果的精确度相对于MPA方法显著提升,楼层侧移均与时程分析结果相近,其中双向地震作用下得出的楼层侧移最为相近;层间位移计算结果中CMPA方法也与时程分析结果较为相近,但y方向和双向地震作用下的3层层间位移有一定误差。
多遇地震作用下与罕遇地震作用下,CMPA方法的计算精度均有所提高,表明该方法适用于SRC框架双向地震分析;与多余地震作用相比,罕遇地震作用下楼层侧移更加接近时程分析结果,但罕遇地震下y方向和双向地震作用下的层间位移仍有一定误差。本文时程分析过程选用3种地震波下结构的地震作用效应平均值作为精确值与Pushover结果进行对比,且需考虑结构多种振型,某个地震波与结构某个振型的周期较为接近时,地震作用效应将被放大。在多遇地震下结构处于弹性阶段受其影响较为明显,在罕遇地震下Pushover可以将结构推覆至极限受力,适当减小了该种情况的影响,因此,与多余地震作用相比,罕遇地震作用下楼层侧移更加接近时程分析结果。

(a) x方向楼层侧移

(c) 双向楼层侧移

(e) y方向层间位移
3.4 型钢混凝土框架Pushover分析
型钢混凝土框架第二阶段Pushover分析中step55、step64、step93的塑性铰如图5所示。
step55、step64、step93分别为结构第一次出现塑性铰、柱端第一次出现塑性铰、推覆结束时结构所有塑性铰的时刻。由图5可知,结构第一次出现的塑性铰为梁端塑性铰,处于框架的二、三层梁端,此时未有框架柱产生屈服,表明该型钢混凝土框架结构很好的实现了“强柱弱梁”的目的。柱端第一次出现塑性铰为框架底层边柱柱端,该柱在单推过程中处于受拉侧,柱中配置型钢弥补了混凝土受拉性能的不足,有效地提高了构件在受拉时的性能,进而提高框架结构在地震中的抗侧力。推覆结束时框架一至五层梁端几乎都出现了塑性铰,一至二层柱端受拉侧也出现了大量的塑性铰,结构可认为已无法继续受力,此时梁端塑性铰的数量远远多于柱端,表明结构很好的实现了“梁铰机制”。型钢混凝土框架经过合理设计同样可实现“强柱弱梁”和“梁铰机制”的结构模式,且配置型钢可使结构抗侧力大大提升,在实际地震中具有更高的安全性。

(a) step55 (b) step64 (c) step93
4 结论
①本文建立了双向地震作用下型钢混凝土框架的两阶段Pushover分析方法:首先对型钢混凝土框架进行振型Pushover,将各振型组合得到的结构位移归一化处理后作为推覆侧移向量对结构进行第2次Pushover分析,得到的地震作用效应即为结构最终的地震响应。
②通过算例分析得出,多遇地震作用下与罕遇地震作用下,两阶段Pushover方法的计算精度较传统Pushover方法和振型Pushover方法均有所提高,表明该方法适用于型钢混凝土框架结构的双向地震分析,与多遇地震作用相比,罕遇地震作用下楼层侧移更加接近时程分析结果。型钢混凝土框架经过合理设计同样可实现“强柱弱梁”的结构模式,且配置型钢可使结构抗侧力大大提升,具有较好的抗震性能。
