组合表面Bragg散射模型共极化SAR海表面风速反演

方贺，杨劲松，樊高峰，李超，史达伟，William Perrie

1.浙江省气候中心,杭州 310051;

2.自然资源部第二海洋研究所卫星海洋环境动力学国家重点实验室,杭州 310012;

3.江苏省气象台,南京 210008;

4.连云港市气象局,连云港 222002;

5.加拿大海洋渔业部贝德福德海洋研究所,达特茅斯NSBY24A 2

1 引言

海表面风场是大气—海洋相互作用的重要纽带，它调节着大气和海洋之间的热量、能量和水气交换，几乎参与了海表面中所有的海水运动过程，在全球气候系统中有着举足轻重的地位。相比于传统的海面风场观测手段（沿海气象站、测风塔和海岛站等），基于卫星遥感技术获取的风场资料有着时空分辨率高、受外界环境影响小以及经济成本低等优势，已经逐渐成为近海风能资源评估的新手段（Bentamy 等，2019）。在众多传感器中，星载合成孔径雷达SAR（Synthetic Aperture Radar）可以不受日照、云以及太阳光线的影响，实现全天时、全天候、高空间分辨率对海成像，从而为全球海洋风能资源的开发和利用提供大范围、高空间分辨率的海洋风场数据（艾未华等，2019）。

SAR 是一种主动式微波传感器，通过向不同粗糙度的海面发射和接收电磁波信号，获取目标海域的雷达后向散射强度，根据海表面风速与后向散射强度、雷达入射角等参数信息间的关系，可以利用相应算法模型直接从SAR影像中提取海面风速信息（方贺等，2018）。对于SAR海表面风场反演，半经验地球物理模型函数GMF（Geophysical Model Functions）是最为常用的手段。目前被广泛应用于C 波段VV 极化SAR 影像风场反演的是CMOD（C-band model）系列GMF，这些模式函数起初是为了VV 极化的散射计的海面风场反演而设计的，后被证明同样适用于SAR风场反演。CMOD系列GMF 定量描述了SAR 归一化雷达后向散射系数NRCS（Normalized Radar Cross Section）和雷达入射角、相对风向和海表面10 m 高处风速间的函数关系，将海面风向、雷达入射角和VV 极化的NRCS 代入CMOD 函数中，通过迭代计算可以快速的获取海面风速信息（Ren 等，2019）。相比于以半经验统计建立的地球物理模式函数，以后向电磁散射理论为基础的海洋微波散射模型具有不受特定微波频率限制的优势，也是SAR 风场反演的研究热点。在后向散射模型中，SAR 影像的NRCS不仅和海面风场有关，还与海浪谱、海水介电常数等其他物理参数相关，虽然其风场反演过程较为复杂，但由于物理模型具有明确的物理含义，因此可以更加深刻地理解SAR 对海洋遥感的内在机理，尤其在亚中尺度涡、海面降水、射流等海洋和大气现象研究中具有广泛的适用性（叶小敏等，2019）。

海表面风通过对海水产生的拖曳作用而改变海面粗糙度，在一定雷达参数和轨道条件下，海面粗糙度是影响SAR 影像后向散射的主要因素。当海面平静无风时，海面起伏较小，雷达发射的电磁波能量返回雷达的主要方式为镜面反射，表现在SAR 图像上较暗；当海面有风时，海面变得粗糙，此时电磁波最主要的回波机制就是布拉格（Bragg）散射。Bragg 散射也称Bragg 共振散射，其内在物理机制实际上是光栅原理，是SAR 对海面成像的最主要回波机制（Plant，1986）。然而，Bragg 散射模型适用于中等局地入射角（20°—70°）和小尺度起伏的粗糙海面情况，而对于小局地入射角情况（0—20°）和大尺度起伏的粗糙海面，几何光学模型则更为适用（Hwang 等，2010；Zhang等，2017）。因此，在不能明确区分低入射角和中等入射角的比较复杂海面的情形下，则一般采用组合表面Bragg 散射模型CSBS（Composite Surface Bragg Scattering）。

CSBS 模型也称为复合双尺度模型CTSM（Composite Two-Scale Model），是海洋微波散射经典模型，它由Bragg 散射模型和几何光学模型组合而成（La 等，2018）。CSBS 模型认为随机海面由大小两种尺度的波浪组合而成，小尺度波（与电磁波波长相当的微尺度波）叠加在大尺度波之上，小区域内的散射均为小尺度波对电磁波产生的Bragg 散射，而长波则通过其倾斜的波面调制短波，改变电磁波的局地入射角，从而对雷达后向散射截面产生影响（杨劲松等，2001；Valenzuela，1967；Donelan 和Pierson，1987；Plant，2002）。在CSBS 模型中，要首先设置局地入射角阈值，用以区分小入射角和中等入射角，随后再由不同的模型进行后向散射信号计算。对于小入射角情况，镜面反射在雷达波的后向散射中占据主导作用，此时NRCS应由几何光学模型计算；对于中等入射角情况，Bragg 散射占主要贡献，此时NRCS 应由Bragg 散射模型计算。然而，如何确定低和中等入射角的界限，即CSBS 模型最优入射角的选取目前尚无定论。

Barrick（1968）认为当局地入射角小于10°时，镜面反射是电磁波雷达后向散射信号强度的主要贡献，此时应使用几何光学模型计算NRCS，并以此为前提对粗糙海面的电磁散射特性进行了研究。Donelan 和Pierson（1987）基于高级应用飞行试验计划AAFE （Advanced Applications Flight Experiment）搭载的Ku 波段Langley 散射计数据分析指出，当局地入射角小于18°时可以认定为低入射角，此时采用几何光学模拟计算NRCS 更为合适。徐丰和贾复（1996）以入射角20°作为低和中等入射角的界限，利用CSBS 模型提出了一种新的风生短波谱形式及散射系数算法。在频率0.428—34.4 Ghz范围内，基于新算法模拟的散射系数与实测数据一致性较好，该算法也为海面微波散射计算提供了一种新的思路。Hwang等（2010）以局地入射角10°为界限，利用CSBS 模型对加拿大RADARSAT-2（RS-2）精细四极化SAR 数据NRCS进行了模拟，并将模拟结果与真实SAR 影像NRCS进行比较。结果显示，基于CSBS 模型仿真的共极化NRCS 与RS-2 观测值具有良好的一致性，且交叉极化NRCS 对高风速更加敏感，并以此为基础阐述了高海况下交叉极化SAR 影像风速反演的应用前景。随后，La 等（2018）基于Sentinel-1 VV 和HH极化地距多视高分辨率影像数据，以10°为入射角阈值，对比分析了CSBS模型和CMOD5.N模式函数仿真的NRCS，并基于仿真的NRCS 进行海表面风速反演。结果显示，基于CSBS模型和CMOD5.N仿真NRCS 的SAR 反演风速具有良好一致性。最近，叶小敏等（2019）在设定10°为入射角阈值的基础上，利用CSBS 模型对RS-2 双极化SAR 影像NRCS 进行了模拟，结果显示CSBS 模型仿真的NRCS 与RS-2 卫星传感器的观测值基本一致，且基于仿真NRCS的SAR反演风速与浮标观测风速误差小于1.71 m/s。

为了探究CSBS 模型中最优局地入射角阈值的选取，使之更好地适用于SAR 风场反演，本文基于142 景RS-2 精细四极化SAR 影像和相应的海洋浮标数据，首先利用CSBS 模型在特定海况下对VV 和HH 极化的SAR 影像NRCS 进行模拟，随后将模拟NRCS 与SAR 观测NRCS 进行比较，从而确定最优局地入射角。最后，在最优局地入射角条件下进行海表面风速反演，以此讨论分析CSBS 模型在星载SAR影像海面风场遥感中的适用性。

2 数据介绍

2.1 RADARSAT-2 SAR影像数据

RADARSAT-2（RS-2）卫星是加拿大航天局CSA（Canadian Space Agency）于2007年12月14日发射的一颗搭载C 波段（5.406 GHz）SAR 的商用雷达卫星，是RADARSAT-1 卫星的后继星，至今仍在轨运行。RS-2 是目前世界上最为先进的星载SAR 卫星之一，可以提供包括精细四极化、超精细模式和多精细模式等在内的20多种卫星影像，并以GeoTiff 数据格式向用户提供（Fang 等，2018）。本文选用的142 景RS-2 SAR 影像均为精细四极化（Fine Quad-polarization）单视复型SLC（Single-look Complex）产品，可以同时提供VH、HV、VV 和HH 4 种极化方式的SAR 影像，各极化通道下影像标称空间分辨率为8 m（方位向）×5 m（距离向），幅宽25 km×25 km，雷达入射角范围25°—35°。

在利用RS-2 SAR 数据进行海面风场反演之前，首先要对原始SAR 影像进行预处理，主要包括辐射定标、几何校正、滤波降噪等。辐射定标是将影像灰度值转化成以分贝（dB）为单位的后向散射系数σ0，从而建立雷达影像强度和探测区域NRCS的定量关系。由于本文选用的精细四极化SLC产品是经过辐射校正后的数据，因此可以直接采用RS-2 用户手册中的定标公式和相关参数对所有像元逐个定标。此外，本文研究对象为海洋且所选SAR 影像均位于开阔海域，海表面相对平缓，起伏度较小，可以忽略由于斜距成像而导致的几何畸变现象，因此本文SAR 影像几何校正仅采用RS-2 数据内product.xml 文件进行地理编码校正。SAR 在对目标成像过程中，会不可避免的产生斑点噪声，从而影响了SAR 影像质量，为了降低噪声信息对海面风场反演的影响，本文选取伽马（GAMMA）滤波法对SAR 数据进行降噪处理（杜培军，2002）。

2.2 海洋浮标数据

海洋浮标具有可靠性高、稳定性好等特点，已经成为海洋环境观测数据的最重要来源之一，因此本文选用海洋浮标观测风场资料作为与SAR反演风场对比的实测数据。根据SAR 影像成像海域，本研究所用RS-2 SAR 影像中130 景位于美国东西海岸的，12 景位于中国东海海域。对于美国东西海岸SAR 影像，本文选用隶属于美国国家浮标数据中心NDBC（National Data Buoy Center）和加拿大环境与气候变化部ECCC（Environment and Climate Change Canada）浮标。对于12 景位于中国东海海域的SAR影像，选用国家海洋局SOA（State Oceanic Administration）提供的沿海浮标。由于SAR 反演风速为海表面10 m 高处风速，因此本文采用风廓线公式将不同高度测风仪观测风速转化为海面10 m高处等效风速（Shao等，2017）。

为了确保SAR 影像和NDBC 浮标的时空一致性，本文规定，空间上每一景SAR 影像内均包含一个海洋浮标，时间上浮标观测数据时间与SAR成像时间间隔不超过30 min。图1所示为一景RS-2精细四极化SAR 影像与NDBC 浮标时空匹配示意图。该SAR 影像成像海域位于美国东海岸，中心经纬度坐标（33°24′25″N，77°44′46″W），成像时间2013-01-16 T 23：13：05 世界协调时UTC（Universal Time Coordinated）。在SAR影像内部包含一个NDBC海洋浮标（#41013，33°26′25″N，77°10′35″W），浮标观测时间为2013-01-16 T 22：50，SAR 成像时间与浮标观测时间相距23 min。

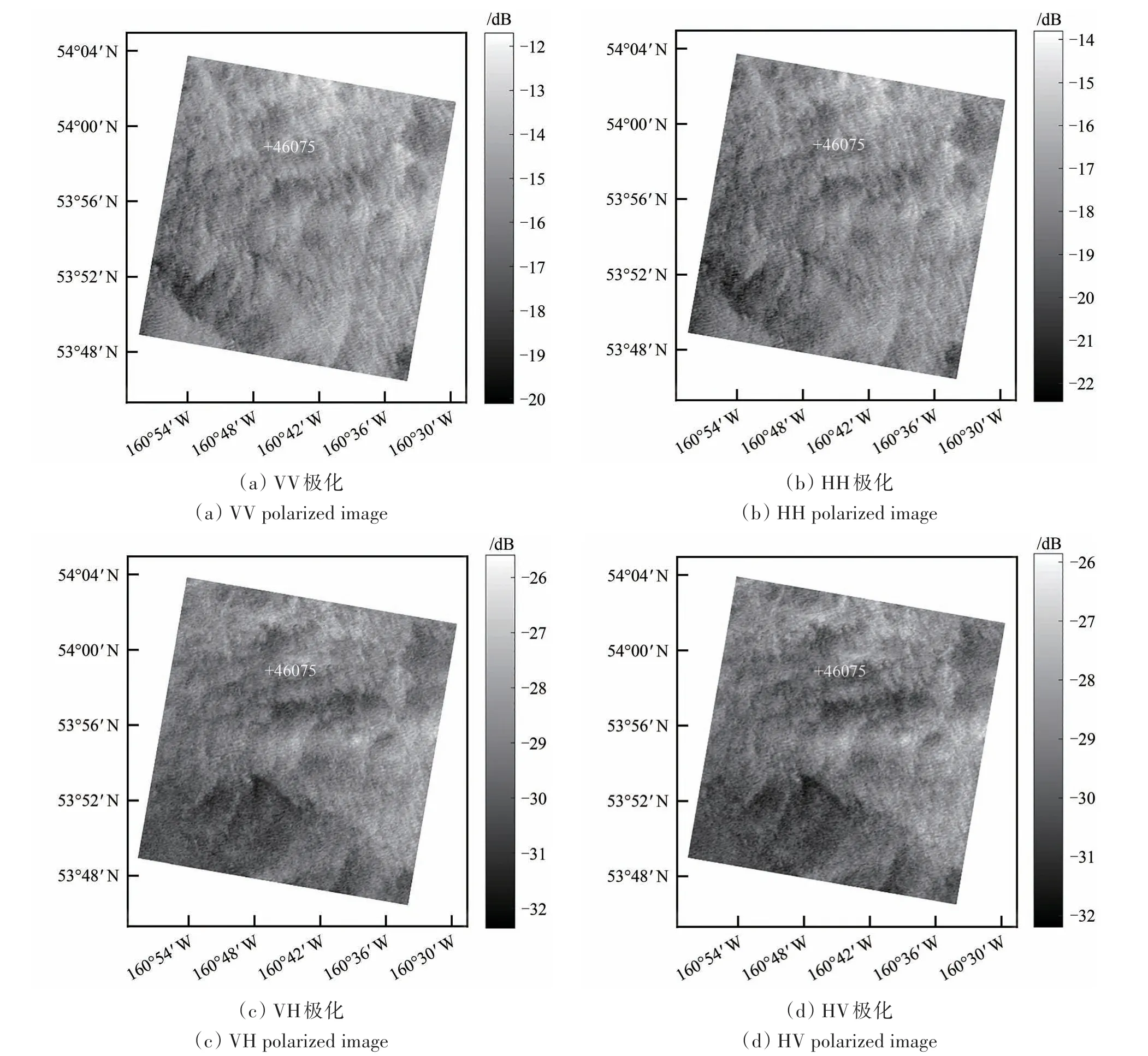
图1 RS-2精细四极化VV、HH、VH和HV极化SAR影像Fig.1 VV，HH，VH and HV-polarized images from RS-2 fine quad-polarization mode SAR

3 SAR风场反演模型

3.1 组合表面布格拉散射模型

组合表面布拉格散射模型（CSBS）包括Bragg散射模型和几何光学模型，该理论始于20世纪60年代，Valenzuela（1978）和Plant（2002）对其进行了详细综述。一般地，CSBS 模型适用于雷达入射角小于70°的情形，此时归一化雷达后向散射系数主要由风生水波的Bragg 散射以及准镜面反射组成。在CSBS 模型中，当局地入射角较小时，可以采用几何光学模型计算NRCS，反之则采用Bragg 散射模型计算NRCS。因此，基于CSBS模型描述的可以表示为

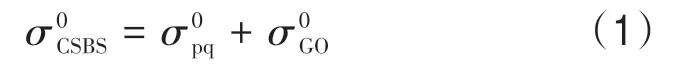
利用经典Bragg 散射模型计算NRCS，要首先计算每个小分辨率单位内的局部散射截面，再利用长波海面斜率概率密度函数，对局部散射截面进行积分。Bragg 所描述的1 阶局部散射截面的解可表示为（Hwang 等，2010；Zhang 等，2017；叶小敏等，2019）

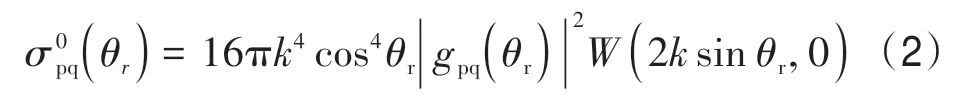
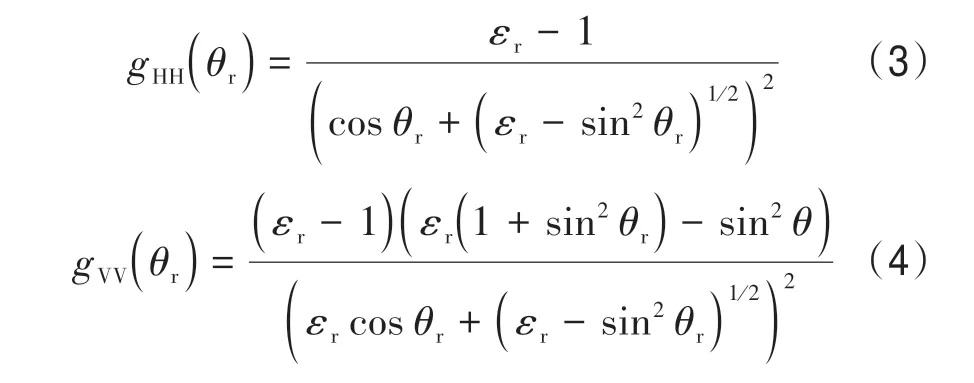
式中，εr表示海面的相对介电常数（Meissner 和Wentz，2004）。对于真实海面而言，海浪的波高一般能达到数英尺，且在大的波浪上还覆盖着小的毛细波，这些小的毛细波使得SAR 所发射的电磁波入射角和极化关系发生改变。因此，对于轻微粗糙倾斜的海面而言，其共极化局地NRCS 的解可表示为

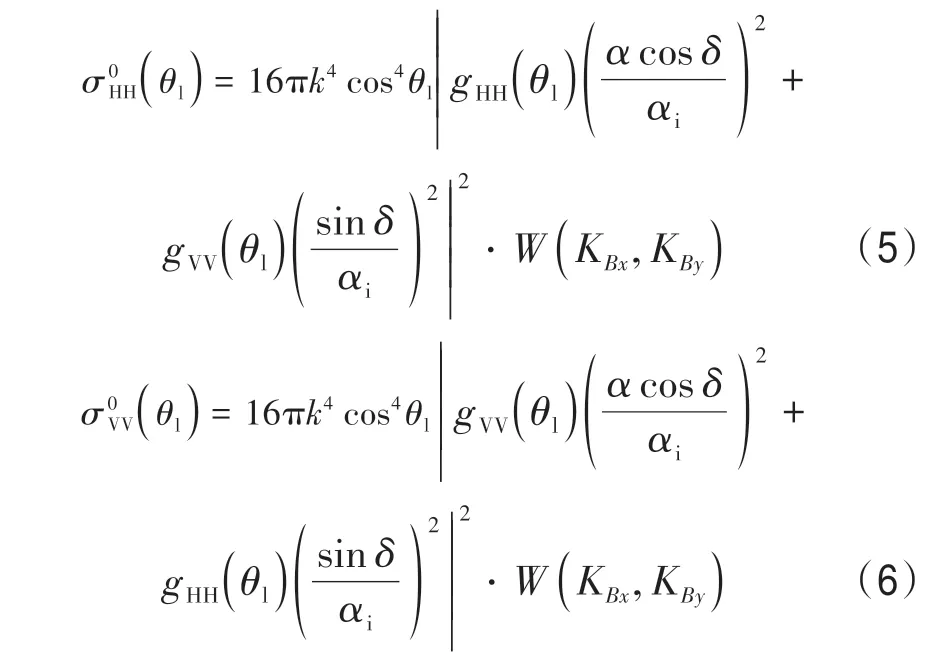
式中，αi= sinθi；KBx= 2kα和KBy= 2kγsinδ分别为Bragg 共振波数的两个分量；α= sin(θl+ψ)，γ= cos(θl+ψ)，其中ψ表示倾斜海面与雷达入射角平面夹角，δ为垂直于倾斜海面的平面与雷达入射角的夹角。电磁波局地入射角θl= cos-1本文中，用于计算和的海浪波数谱用方向谱代替，其中KB= 2ksinθr为布拉格波数，φB为Bragg 波矢量方向，S(K，φ)为波浪方向谱，φ为相对于风向的波矢量方向。在前人的研究中，Elfouhaily 海浪方向谱可以较好应用于CSBS 模型中，其方向谱二维波数是海表面风速和方向（对于风向的角度）的函数（Thompson 等，2012；La 等，2018；叶小敏等，2019），因此本文选用Elfouhaily 海浪谱利用CSBS 模型求解VV 和HH极化的NRCS。

考虑海面所有长波坡度情况，整个海面NRCS可由积分形式表示为

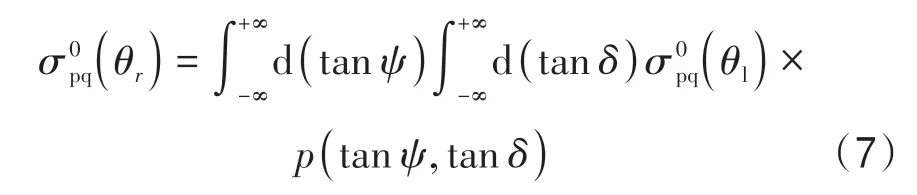
式中，p(tanψ，tanδ)为沿垂直海面方向观测的海面斜率概率密度函数PDF （Probability Density Function），可由Gram-Charlier 分布函数表达（Cox和Munk，1954；Zhang等，2017）：

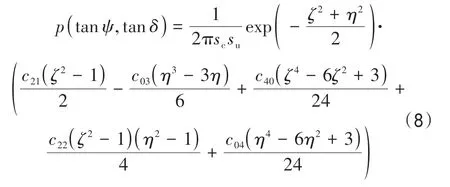
式中，c40= 0.4；c22= 0.1；c04= 0.2；c21=-0.11u10/14；c03=-0.42u10/14；η= tan(ψ/su)和ζ= tan(δ/sc)表示迎风和侧风时的归一化斜率分量；和表示迎风和侧风时海面粗糙度的均方坡度；u10和u12.5分别表示海表面10 m 和12.5 m 高处风速，海面不同高处风速可由风速廓线公式进行转换（Shao 等，2017）。对于小入射角情况，镜面反射是电磁波后向散射的主要贡献，此时海面NRCS由几何光学模型计算更为合适。几何光学模型对NRCS 的描述可由下式表达（Hwang 等，2010；叶小敏等，2019）：

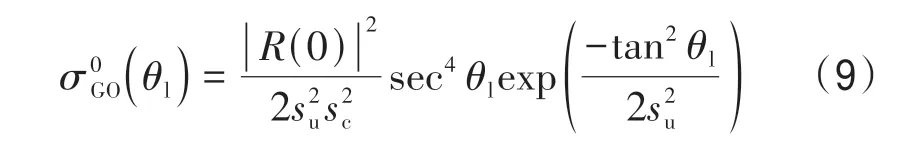
式中，R为菲涅尔反射系数，垂直入射的菲涅尔发射系数|R(0)|2对VV 极化和HH 极化相等，表示式如下：

综上所述，在给定海表面风速、风向、雷达入射角和方位角的前提下，当局地入射角较小时，可用几何光学模型式计算NRCS，当局地入射角为中等入射角时，可由Bragg 散射模型求解NRCS。同样地，将VV 和HH 极化SAR 影像NRCS、雷达入射角、方位角和海面风向输入CSBS 模型，也可以计算得出海表面风速信息。对于小和中等局地入射角的界限，学者们给出了不同的数值，Hwang等（2010）、La 等（2018）和叶小敏等（2019）认为小于10°时为低局地入射角，Donelan 和Pierson（1987）认为小于18°为低入射角，徐丰等（1996）认为小于20°为低入射角。

3.2 地球物理函数风速反演模型

CMOD系列地球物理函数模型是一种半经验模型，起初是基于VV 极化的散射计数据开发的，后被证实同样适用于C 波段SAR 海面风场反演。CMOD 模式函数描述了海表面10 m 高处风速与VV极化的NRCS、雷达入射角以及相对风向的关系。CMOD 函数有众多版本，其中应用较为广泛的有CMOD4、CMOD-IFR2、CMOD5 和CMOD5.N。方贺等（2018）选取成像于以美国东西海岸的RS-2精细四极化SAR 影像，利用CMOD5.N 模式函数开展风速反演实验，并将SAR 反演风速与NDBC 浮标风速进行对比。结果显示，基于CMOD5.N 函数的SAR 反演风速与NDBC 观测风速均方根误差为1.68 m/s，满足海面风速反演要求。因此，本文选用CMOD5.N 函数作为RS-2 VV 极化SAR 影像风速反演模型。CMOD5.N 函数表达式如下（Hersbach，2010）：

对于HH 极化SAR 影像，无法通过CMOD5.N模式直接求解风速，通常的做法HH 极化NRCS通过极化比模型转化为VV 极化的，然后再代入CMOD5.N 函数求解风速。基于877 景RS-2 精细四极化SAR 影像，Zhang 等（2011）提出了一种仅和入射角有关的指数形式极化比模型（简称Z2011 模型），利用该模型的HH 极化SAR 反演风速与浮标风速具有良好的一致性，两者RMSE为1.86 m/s。此外，Z2011 模型所使用的SAR 影像数据与本文选取SAR 影像均为精细四极化，因此本文采用Z2011 模型作为HH 极化SAR 反演风速的极化比模型。Z2011极化比模型表示如下：

式中，θr为雷达入射角；A、B和C为系数，其取值分别为0.2828，0.0451和0.2891。

4 最优入射角查找算法

CSBS 模型由Bragg 散射模型和几何光学模型组合而成，且在中等局地入射角情况下，Bragg 散射是SAR 对海面成像的主要机制，此时局地雷达NRCS 由Bragg 模型计算；在小局地入射角情况下，镜面反射是SAR 后向散射的主要贡献，此时NRCS由几何光学模型计算。然而，如何界定小和中等入射角的阈值，目前尚无定论。基于此，本节首先利用142景RS-2精细四极化SAR原始影像数据，首先在海洋浮标经纬度处提取包括VV 和HH 极化NRCS、局地入射角、海表面风速和海面风向在内的相应参数信息。随后，基于统计性方法建立最优局地入射角查找算法，通过设定不同入射角阈值对比分析CSBS模型仿真的与RS-2影像浮标处观测的的关系，从而寻找最优入射角。最优入射角查找算法演示图2所示，其具体计算流程分为以下几个步骤：

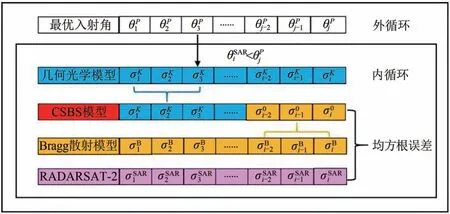
图2 最优入射角查找算法框架图Fig.2 Frame diagram to find the best incidence angle

（2）建立3 个元素个数为i一维矩阵，分别表示几何光学模型仿真的、Bragg 散射模型仿真的和RS-2 SAR影像的；

（3）最优入射角查找模型由双层循环体构成。内层循环用于计算仿真和的均方根误差，外层循环用于确定最优入射角。在外循环体中，建立最优局地入射角矩阵，其元素取值规则如下：以5°为初值，45°为终值，步长为1°；

（5）因此，在局地入射角5°—45°范围内，每次选定一个入射角，均可生成一个矩阵，且每次都计算矩阵和矩阵的均方根误差。当所有循环结束，最小均方根值所对应的入射角，即为CSBS模型最优入射角。

利用142 景VV 和HH 极化的RS-2 四极化SAR影像、Bragg 散射模型和几何光学模型，本文分别计算了不同入射角下的CSBS 模型仿真NRCS 与RS-2 影像NRCS 的RMSE。图3所示为CSBS 模型矩阵与RS-2 SAR 矩阵的RMSE 随入射角的变化。图3 可以看出，无论是VV 还是HH 极化SAR 数据，基于CSBS 模型仿真的NRCS 与RS-2 观测NRCS 的RMSE 均呈现先减小再变大的趋势。由图3 可知，对于VV 极化SAR 数据，CSBS 模型仿真的NRCS和SAR 影像观测NRCS 的RMSE 在局地入射角为14°时达到最小，为1.94 dB，因此14°即为VV 极化数据的最优入射角。图4（a）所示为VV 极化RS-2影像NRCS与CSBS模型仿真NRCS在局地入射角为14°时的对比，两者偏差为-0.29 dB，相关系数0.89，具有良好的一致性。在给定雷达入射角、浮标风向以及海面10 m 高风速的条件下，图4（b）还分析了CMOD5.N 仿真的VV 极化NRCS 和RS-2影像NRCS 的关系，两者RMSE 为1.71 dB，偏差为-0.18 dB，相关系数0.91，具有良好的一致性。

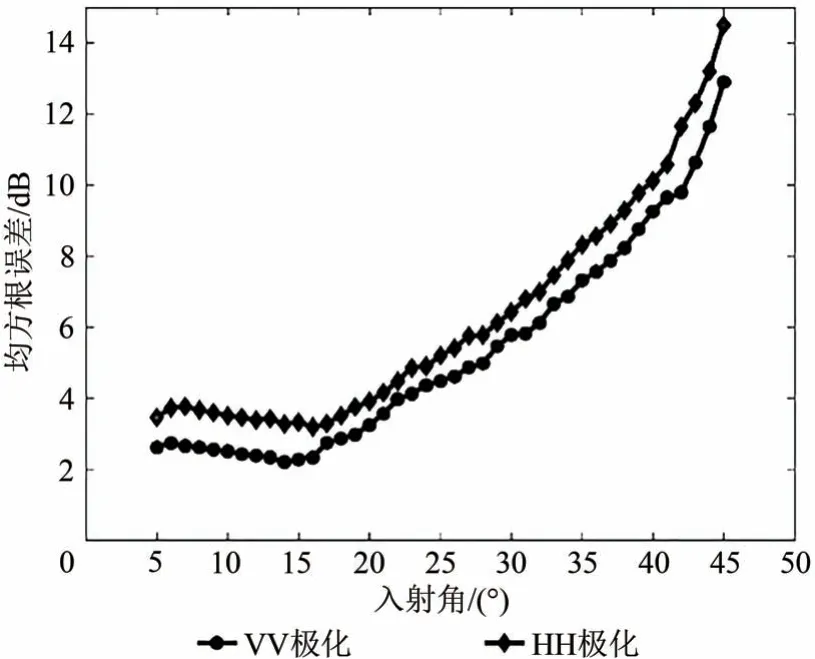
图3 CSBS模型仿真NRCS和RS-2影像NRCS均方根误差随入射角的变化Fig.3 The RMSE of NRCSs between RS-2 SAR images and CSBS model simulated at different local incidence angle

图4 VV极化通道下RS-2影像、CSBS模型和GMF模式函数NRCS比较Fig.4 The relationship of NRCS from RS-2 images，CSBS model and CMOD5.N function at VV-polarization channel

基于HH 极化数据的CSBS 模型仿真NRCS 和SAR 影像观测NRCS 的RMSE 在局地为入射角为16°时达到最小，为2.92 dB，因此16°即为HH 极化数据的最优入射角。图5（a）所示为HH 极化RS-2 影像NRCS 与CSBS 模型仿真NRCS 在局地入射角为16°时的对比，两者偏差为-0.36，相关系系数0.87，具有良好的一致性。与此同时，在相同海况条件下，图5（b）还分析了HH 极化RS-2影像NRCS和CMOD5.N+Z2011组合模型仿真NRCS的关系，两者RMSE 为2.11 dB，偏差-0.12 dB，相关系数0.88，具有良好的一致性。

图5 HH极化通道下RS-2影像、CSBS模型和CMOD5.N+Z2011模式函数NRCS比较Fig.5 The relationship of NRCS from RS-2 images，CSBS model and CMOD5.N function at HH-polarization channel

通过上述分析可知，在相同海况条件下，基于最优局地入射角的CSBS 模型仿真共极化NRCS和地球物理模式函数模拟的共极化NRCS均与RS-2影像观测的共极化NRCS有着良好的一致性，这也是CSBS 模型和地球物理模式函数可以有效地从SAR影像中提取风速的理论基础。

5 基于最优入射角的CSBS 模型反演风速

由上文分析可知，对于VV 极化SAR 影像，当局地入射角≥14°时可由Bragg 散射模型计算海面风速，当入射角<14°，可由几何光学模型计算风速；对于HH 极化SAR 影像，当入射角≥16°时，可由Bragg 散射模型计算海面风速，当入射角<16°，可由几何光学模型计算风速。基于此，本节利用CSBS 模型在最优局地入射角条件下对142 景RS-2精细四极化SAR影像开展海面风速反演实验。

图6（a）和（b）所示为一景精细四极化RS-2 VV 和HH 极化SAR 影像，该SAR 影像成像中心经纬度坐标（40°12′23″N，73°15′22″W），成像时间2013-01-18 T 10：58：59 UTC。图中红色“+”表示NDBC 海洋浮标（#44025，40°15′3″N，73°9′52″W），浮标观测时间为2013-01-18 T 10：50，浮标观测海表面10 m 高处风速为8.59 m/s，风向为357°。图6（c）和（d）所示分别为利用CMOD5.N 模型函数的VV 极化SAR 反演风速和利用CMOD5.N+Z2011 组合模型的HH 极化SAR 反演风速。在浮标经纬度处，基于VV 极化影像的CMOD5.N GMF 反演风速为6.92 m/s，和浮标风速误差1.67 m/s；基于的HH 极化影像的CMOD5.N+Z2011 组合模型反演风速为6.76 m/s，和浮标风速误差为1.83 m/s，满足海表面风速反演要求。图6（e）和（f）所示分别为在最优入射角下基于VV 和HH 极化SAR 影像的CSBS 模型反演风速。在浮标经纬度处，基于VV 极化影像的CSBS 模型反演风速为7.68 m/s，和浮标风速误差0.91 m/s；基于HH 极化影像的CSBS模型反演风速为7.35 m/s，和浮标风速误差为1.24 m/s，满足海表面风速反演要求。由此可见，无论是CSBS 模型还是地球物理函数模型，均能从VV 和HH 极化SAR 影像中提取风速，且基于各模型的SAR反演风速与浮标风速有着良好的一致性。

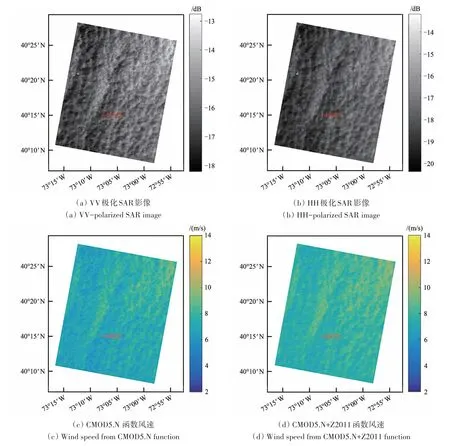
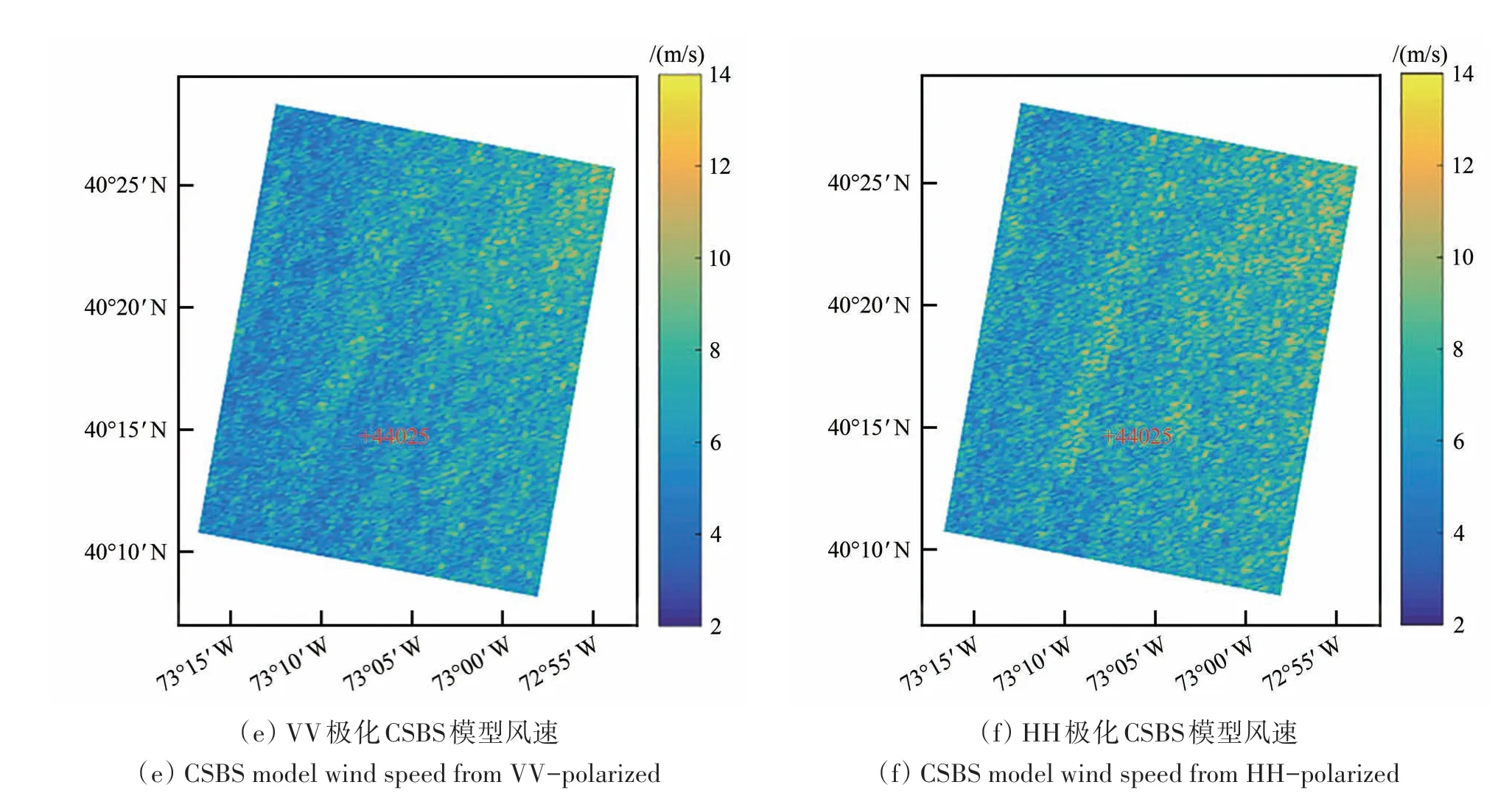
图6 SAR原始影像及相应模型反演风速Fig.6 SAR raw images and wind speed retrieve from corresponding models

根据上述风速反演流程，本节在VV 和HH 极化影像最优局地入射角条件下，利用CSBS 模型对142 景RS-2 精细四极化进行海表面风速反演，并将结果与海洋浮标观测风速进行比较。图7所示为在不同局地入射角选取条件下，基于VV 和HH 极化数据的SAR 反演风速与浮标观测风速RMSE 变化。在局地入射角为14°时，基于VV 极化数据的CSBS 模型反演风速与浮标风速RMSE 达到最小，为2.15 m/s，因此可以认为SAR 反演风速效果在入射角为14°时优于其他入射角。对于HH 极化SAR数据，在局地入射角为16°时CSBS 模型反演风速与浮标风速RMSE 达到最小，为2.32 m/s，即SAR 反演风速精度在入射角为16°时要高于其他入射角。

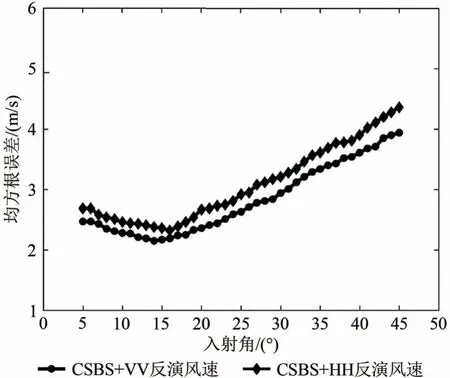
图7 不同入射角条件下CSBS模型反演风速与浮标风速均方根误差Fig.7 The RMSE variation between CSBS-retrieved wind speed and buoy measured wind speed at different local incidence angles

为了直观地展示CSBS 模型在最优局地入射角的风速反演效果，图8（a）（b）所示分别为最优入射角条件下基于VV 极化和HH 极化SAR 影像的CSBS 模型反演风速与浮标风速散点图。图8 中可以看出，基于VV和HH极化数据的CSBS模型反演风速与浮标风速一直性较好，与浮标风速RMSE分别为2.15 m/s 和2.32 m/s，相关系数分别为0.79 和0.75。此外，本文还比较了基于VV 和HH 极化数据的CMOD5.N 模式函数反演风速和CSBS 模型反演风速。图8（c）为基于VV 极化数据的CSBS 模型和CMOD5.N 函数风速反演对比，两种模型反演风速RMSE 为1.81 m/s，相关系数为0.86，偏差为-0.25 m/s，两者具有良好的一致性。图8（d）所示为基于HH 极化数据的CSBS 模型和CMOD5.N+Z2011 组合模型风速反演对比。相比于VV 极化数据，CSBS模型和CMOD5.N+Z2011组合模型反演风速RMSE 较大，为2.47 m/s，产生这一现象的原因可以解释为：无论是CMOD5.N （CMOD5.N+Z2011）模式函数还是CSBS 模型，其反演风速数值均与海面NRCS有着直接关系，即风速反演模型是NRCS 的函数。对于VV 极化影像，在雷达入射角和相对风向确定的前提下，VV 极化的NRCS 可以直接代入CMOD5.N 或CSBS 模型求解风速，因此两种模型反演风速差异性较小。然而，对于HH极化的SAR 而言，利用CMOD5.N 函数反演风速需借助极化比模型进行转换，虽然Z2011极化比模型是基于RS-2 精细四极化影像建立的，但由于建立模型时数据源以及研究区域不同，利用其对本文HH 极化数据进行风速反演时，会不可避免的产生误差，从而导致CMOD5.N+Z2011 组合模型反演风速与CSBS模型反演风速产生一定的误差。

图8 CSBS模型反演风速与浮标风速和GMF函数反演风速比较Fig.8 The relationship of wind speed between CSBS model，buoy and GMF function

6 结论

以后向电磁散射理论为基础的组合表面布拉格散射模型（CSBS）由Bragg散射模型和几何光学模型组成，是海洋微波散射的经典模型，与半经验的地球物理函数模式相比，具有不受特定微波频率限制的优势。前人研究指出，Bragg 散射模型仅适用于中等局地入射角，而几何光学模型可应用于小入射角情形，但如何确定中等和小入射角的阈值，即CSBS 模型最优入射角的选取目前尚无定论。本文基于142 景RS-2 精细四极化SAR 影像数据和海洋浮标数据，建立了最优入射角查找模型，分别对VV 和HH 极化SAR 数据进行最优入射角阈值的选取。结果显示，当局地入射角为14°时，CSBS 模型仿真的VV 极化NRCS 与RS-2 VV 影像观测NRCS 均方根误差最小，当局地入射角为16°时，CSBS 模型仿真的HH 极化NRCS 与RS-2 HH影像观测NRCS均方根误差最小。因此，14°和16°分别为VV 和HH 极化影像CSBS 模型反演风速最优入射角。随后，在最优入射角前提下，本文利用CSBS 模型分别对142 景RS-2VV 和HH 极化SAR 影像开展风速反演实验，并将反演风速与浮标风速进行对比。结果显示，基于VV 极化数据的CSBS 模型反演风速与浮标风速RMSE 为2.15 m/s，基于HH 极化数据的CSBS 模型反演风速与浮标风速RMSE为2.32 m/s，满足SAR海面风速反演要求。

SAR 作为一种全天时、全天候的高分辨率主动式微波成像雷达，在海洋遥感探测尤其是海表面风场观测方面发挥着重要作用。本文以经典组合表面散射模型为研究对象，利用统计性分析方法，给出了利用VV 和HH 极化数据求解风速时的最优局地入射角数值，使该模型适用于小至中等入射角。值得指出的是，海况对于最优入射角的选取具有重要影响，其原因在于无论是利用CSBS模型还是CMOD 系列地球物理函数，其反演风速均与海况呈正相关，即海况越高，海表面粗糙越大，雷达后向散射回波信号强度（NRCS）越强，这也是SAR 影像可以求解风速的基本原理。由于数据量有限，本文选取的142 景RS-2 精细四极化SAR 影像海况区间为0—15 m/s，且0—10 m/s 区间内影像数量为103 景，约占整体SAR 数据的80%。因此，本研究最优局地入射角的选取在低海况条件下更加适用。从风速反演效果看，本文提出的最优入射角适用于C 波段RS-2 精细四极化SAR 影像风速的反演。在以后的研究中，还将利用更多的SAR 影像数据尤其是高海况下数据进一步研究CSBS 模型最优入射角的选取，同时也会关注CSBS模型在交叉极化SAR数据中的应用情况。

志 谢本文使用的RADARSAT-2 精细四极化SAR 影像数据由加拿大贝德福德海洋研究所BIO （Bedford Institute of Oceanography）William Perrie教授提供，原始影像产品版权归MacDonald，Dettwiler 和Associates Ltd 公司所有，海洋浮标数据由美国国家数据浮标中心NDBC（National Data Buoy Center）、加拿大环境与气候变化部ECCC（Environment and Climate Change Canada）和中国国家海洋局SOA（State Oceanic Administration）提供，在此表示感谢！