联合星载高光谱影像和堆栈集成学习回归算法的红树林冠层叶绿素含量遥感反演

付波霖，邓良超，张丽，覃娇玲，刘曼，贾明明，何宏昌，邓腾芳，高二涛，范冬林

1.桂林理工大学测绘地理信息学院,桂林 541006;

2.中国科学院空天信息创新研究院,北京 100094;

3.中国科学院东北地理与农业生态研究所,长春 130000

1 引言

红树林（Mangrove）主要生长在热带、亚热带海岸线潮间带，由红树植被为主体的常绿灌木和乔木组成耐盐湿地木本植被群落（Cao等，2018）。红树林具有“海岸肾”功能，有护堤固滩、防风减浪、保护农田、降低盐害、净化水质、促淤造陆、固碳作用和鸟类栖息等生态价值。由2019年4月自然资源部、国家林草局联合组织的红树林资源和适宜恢复地专项调查结果表明：广西壮族自治区是中国红树林的重要分布区，红树林总面积为9330.34 ha，占全国红树林总面积（2.89万ha）的32%，居全国第二位；广西壮族自治区钦州市红树林总面积达3078.73 ha，占全区总面积的32.99%，仅次于北海市（4192.78 ha）。病虫害、物种入侵和海区污染等环境因素严重威胁着广西壮族自治区钦州市红树林的健康生长，CCC 是衡量红树林健康状况的重要指标之一（Wang 等，2019；Ali 等，2020），因此，利用遥感方法进行大规模高精度反演红树林的CCC对于监测红树林的健康状况具有重要意义。

目前，获取植被生物物理参量的方法主要包括地面测量方法和遥感反演方法。由于红树林多生长在含水的泥滩和潮滩上，传统地面测量方法耗时费力，且难以对生物物理参量进行大规模的测量（Kamal 等，2016），所以亟需一种对红树林生物物理参数进行高精度估算的遥感方法。Lou等（2021）通过随机森林（RF）回归模型的参数优化进一步提高GF-1 WFV、Landsat 8 OLI 和Sentinel-2 MSI尺度上反演沼泽湿地植被CCC 的精度，其中MSI的反演精度最高，R2为0.79，RMSE为10.96 SPAD。多光谱卫星影像光谱分辨率较低，不能充分包含与植被生物物理参量高度相关的光谱细节信息。Wu 等（2010）利用EO-1 Hyperion 高光谱卫星数据计算的EVI植被指数可以表现出适度的抗饱和能力，在估算玉米冠层叶绿素含量中R2达到0.81。George 等（2018）利用EO-1 Hyperion 高光谱卫星数据对印度安达曼岛中红树林CCC 进行光谱指数敏感性评估，发现Hyperion 数据波谱带中549 nm、559 nm、702 nm、722 nm、742 nm 和763 nm 对红树林CCC 最为敏感，比值植被指数（SR）的相关性最高，R2为0.75。目前，国外的高光谱卫星数据实现了对红树林CCC 的有效估算，但国产珠海一号高光谱卫星数据在红树林CCC 反演中的可靠性仍有待进一步验证。

高光谱卫星传感器提供了几十、上百甚至几千个光谱波段（童庆禧等，2016），尽管丰富的光谱信息可以提供植被覆盖层或叶片的吸收特征更多的细节信息，但冗余波段反而会降低反演精度。Lee 等（2004）和Liu 等（2016）利用机载高光谱影像估算农作物叶面积指数LAI（Leaf Area Index），论证了使用高相关性光谱波段和增加对LAI不敏感的波段，均会降低模型反演LAI 的准确性。因此，高光谱影像特征降维在植被生物物理参数定量反演方面是不可或缺的。目前特征变换（PCA、MNF和ICA等）和特征选择（REF、OIF和K-means等）算法已成为解决高光谱数据中信息冗余问题的主要方法（Jain 等，2000）。程志庆等（2015）基于最佳指数—相关系数法选取的高光谱数据最佳组合波段（760 nm、1860 nm 和1970 nm），在反演冬小麦叶片叶绿素含量中相较于最佳指数法和最大相关系数法的精度最高（R2=0.827，RMSE=5.44）。最大相关系数法方法仅考虑了变量与目标值的相关性，容易忽略其他因素的间接作用，最佳指数法方法虽能获得信息量丰富、冗余度小的波段组合，但不能保证所选波段与植被参量之间具有最大相关性，最佳指数—相关系数法虽然综合了两者的优点，但是无法定量评估每个变量的重要性。Chen 等（2020）基于特征选择的RF 算法与K 近邻（KNN）回归的组合模型（R2=0.834，RMSE=0.824）实现了玉米LAI 的可靠估计。基于CART 的特征选择方法，可以评价每个变量对于模型构建的贡献率（Sylvester 等，2018），但是在变量选择中过多的数据维度会增加与波长选择相关的信息损失，因此，应先采用保持特征与目标值之间最大相关性的数据降维方法最大程度降低数据的维度，再进行特征重要性评价。目前在植被生物物理参数的反演中，综合最大相关系数法与基于CART模型的特征选择方法应用于高光谱数据降维，提升模型反演精度的可能性仍有待进一步验证。

目前遥感反演植被生物物理参数的经验统计回归模型主要分为简单线性和非线性回归模型。为了探究多种植被指数反演叶片叶绿素a 含量LCC（Leaf Chlorophyll-a Content）的可行性，Zhen 等（2021）基于4 个时期的Sentinel-2 卫星数据，得到单波段反射率与两波段反射率之和比值指数（RSSI）的线性回归模型反演LCC 的调整R2为0.496、 0.742、 0.681 和0.801， RMSE 为5.75、4.29、4.00 和3.46 SPAD，优于传统波段指数的核岭回归（KRR）模型。线性回归模型可以有效降低反演过程中的不确定性（Lin 和Lin，2019），但对于非线性或特征间具有高相关性的数据，线性回归模型难以建模。为了准确估计红树林地区的LAI 指数，Zhu 等（2017）利用人工神经网络（ANN）回归、支持向量机（SVM）回归和RF 回归模型探讨WorldView-2影像红边波段计算的植被指数对红树林LAI 的敏感性，结果表明RF 回归模型的估算精度最高（RMSE=0.45），SVM 回归模型的估算精度（RMSE=0.51）低于另外两种反演模型。机器学习回归算法可以平衡数据集的误差，容易并行化，模型泛化能力比较强。非线性回归模型能较好地解释生物物理参数与模型参数之间的关系（唐少飞等，2020），但如果单一回归模型的预测误差都比较低，则经常需要权衡模型的平衡性与准确性（Christensen，2003）。Ghosh 等（2021）在估算富含碳的印度红树林地上生物量（AGB）时，采用多时相图像堆栈数据集和单一RF回归模型估算AGB 的RMSE 为74.493 t/ha，优于单个数据集（RMSE=151.149 t/ha），多时相图像堆栈数据集中采用堆栈算法反演AGB 的精度得到了进一步的提高，RMSE 为72.864 t/ha，集成回归模型可以集成不同算法的预测结果，并产生更稳健的估算结果。基于堆栈的集成回归算法可以集成多种基础回归模型，并且在回归预测上提供更好的泛化能力（Dietterich，2000）。目前，利用基于堆栈的集成学习回归模型反演红树林CCC 还有待深入研究。

综上所述，为了实现北部湾红树林CCC 高精度遥感反演，本文主要研究内容如下：（1）构建红树林CCC 反演多维特征数据集，并利用最大相关系数法与基于CART模型的特征选择方法对红树林高维特征数据集降维处理；（2）构建单一线性回归、机器学习回归模型与堆栈集成学习回归模型反演红树林CCC，并验证单一线性回归、机器学习回归模型与堆栈集成学习回归模型反演红树林CCC 的精度；（3）验证珠海一号高光谱卫星和Sentinel-2A数据反演红树林CCC的适用性，并对比两种数据源反演红树林CCC的精度差异；（4）评估SNAP-SL2P 算法反演红树林CCC 的适用性，并定量分析SNAP-SL2P 算法与最优回归模型估算红树林CCC的精度差异。

2 研究区概况与数据源

2.1 研究区概况

研究区位于广西北部湾大风江沿岸（图1（a））的钦州市犀牛脚镇苏屋村（图1（b））和沙角村（图1（c））。地理坐标为21°37′00″N—21°38′20″N，108°48′15″E—108°52′15″E，属于亚热带季风型海洋性气候。钦州市的夏季长达6个月之久，全年平均气温为22℃，年均降水量达2104.2 mm，相对湿度为81%，夏秋两季是湿热多雨的季节，为红树林的生长提供了温暖舒适的环境。研究区内红树林总面积约为2.41 km2，主要分布着3 类树种：白骨壤、桐花树和秋茄，其中白骨壤分布面积最大。根据实地采集数据计算白骨壤的平均高度为1.81 m，平均冠幅为4.30 m2；桐花树平均高度为1.41 m，平均冠幅为0.93 m2；秋茄的平均树高为0.84 m，平均冠幅为1.25 m2，树高和冠幅的优势使得白骨壤成为该地区的优势种群。研究区内的红树林主要经受外滩互花米草的入侵和病虫害的胁迫。因此，利用遥感手段对红树林CCC 进行大规模高精度的估算，对红树林的监测和保护有着重要意义。

图1 研究区位置及实测点分布Fig.1 The location of the study area and the distribution of filed measurements

2.2 珠海一号高光谱卫星数据及预处理

珠海一号高光谱卫星（OHS）采用推扫模式单次拍摄影像成像，搭载CMOSMSS 传感器，影像空间分辨率为10 m，光谱分辨率为2.5 nm，波段数为32 个，波长范围为400—1000 nm。本文OHS数据下载网址为：https://www.obtdata.com/，获取影像时间为2021年1月12日，产品级别为L1 级，整景影像云量为1%，研究区内无云覆盖。OHS 数据文件中包括32 个光谱波段的tif 格式的文件与其对应的用于正射校正的RPC文件。

OHS 数据预处理的流程如下：（1）分别利用ENVI 5.6 软件下的Radiometric Calibration、FLAASH Atmospheric Correction 模块进行辐射定标和大气校正；（2）利用ENVI 5.6软件的RPC Orthorectification Workflow 模块和GMTED2010.jp2 DEM 数据进行无控制点正射校正；（3）利用GNSS RTK 的控制点进行影像配准，在ENVI 5.6 的Registration：Image to Map 模块中生成WGS_1984_UTM_Zone_49N 坐标系的影像，配准误差RMSE为0.42，并进行裁剪。

2.3 Sentinel-2A数据及预处理

哨兵2 号（Sentinel-2）为多光谱成像卫星，本文下载Sentinel-2A 数据的网址为：https://earthexplorer.usgs.gov/，获取时间为2021年2月19日，产品级别为L1C 级，整幅影像云量为0.319%，研究区上空无云层覆盖，需要进行辐射定标、大气校正及重采样等预处理。

Sentinel-2A数据处理过程为：（1）使用Sen2Cor v2.8 软件进行辐射定标和大气校正；（2）利用SNAP 软件下的S2 Resampling Processor 工具将所有波段重采样成10 m 空间分辨率的影像；（3）利用GNSS RTK 的控制点进行影像配准，在ENVI 5.6的Registration：Image to Map 模块中生成WGS_1984_UTM_Zone_49N 坐标系的影像，配准误差RMSE为0.58，并进行裁剪。

2.4 红树林LAI及LCC实地测量

本次实测数据采集时间是2021年1月8日至2021年4月6日，一共采集了219个10 m×10 m的样方，红树林CCC由LCC与LAI的乘积得到（Gitelson等，2005）。本文利用LAI-2200 Plant Canopy Analyzer 仪器测量红树林的LAI 数据，利用Chlorophyll Meter SPAD-502 Plus 仪器测量红树林叶片的LCC 数据，并用中海达V90 GNSS RTK 记录采集地面点的地理位置。为了高精度地反演红树林CCC，10 m×10 m 的地面实测样方尽量均匀分布整个研究区（图1），采集数据见表1。研究区内白骨壤、桐花树及秋茄中LAI的数值范围分别为0.75—2.83、1.62—4.03和1.44—2.72；白骨壤、桐花树及秋茄中LCC的数值范围分别为36.60—58.00 μg/cm2、40.40—57.00 μg/cm2和56.40—66.00 μg/cm2。

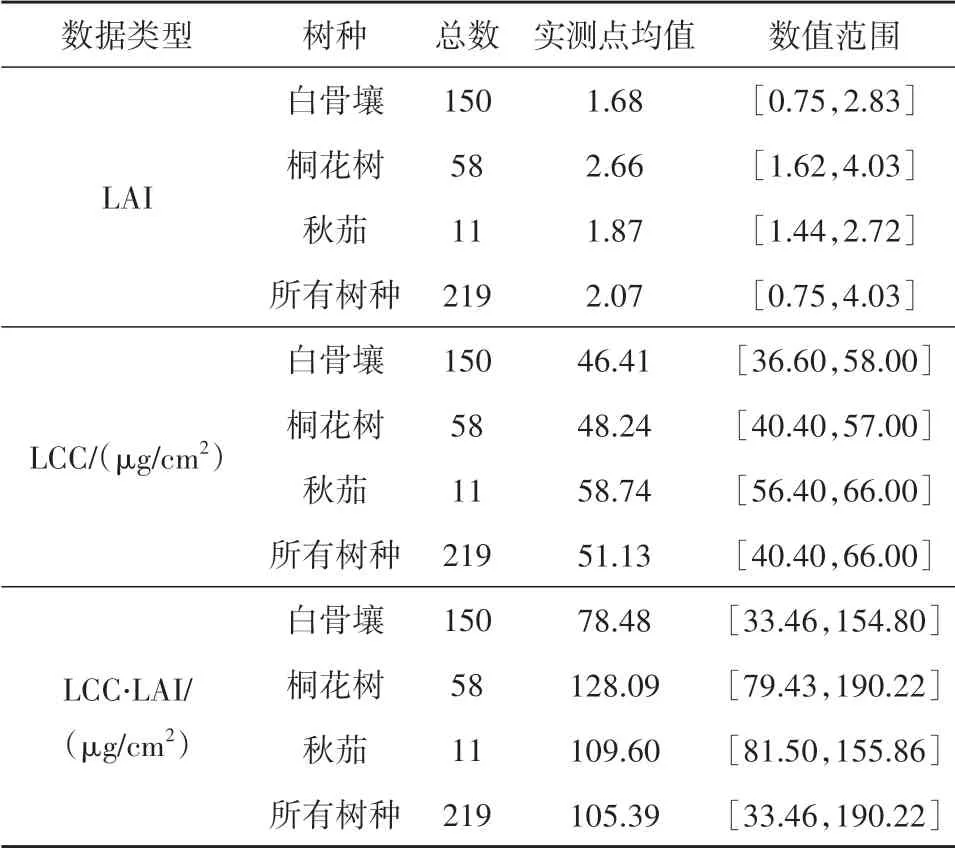
表1 研究区内地面实测的LAI和LCC数据统计Table 1 Statistics of LAI and LCC values derived from field measurements in the study area

3 红树林CCC遥感反演方法

3.1 多源数据集生成与统计检验

3.1.1 植被指数与组合植被指数计算

OHS 及Sentinel-2A 数据预处理后，影像的DN值转换成了地面物体实际的反射率信息，提取后的反射率信息用于计算植被指数与组合植被指数。本文通过ENVI 5.6 软件的Band Math 工具分别计算了OHS 和Sentinel-2A 数据的10 种传统植被指数，具体类型及公式见表2。

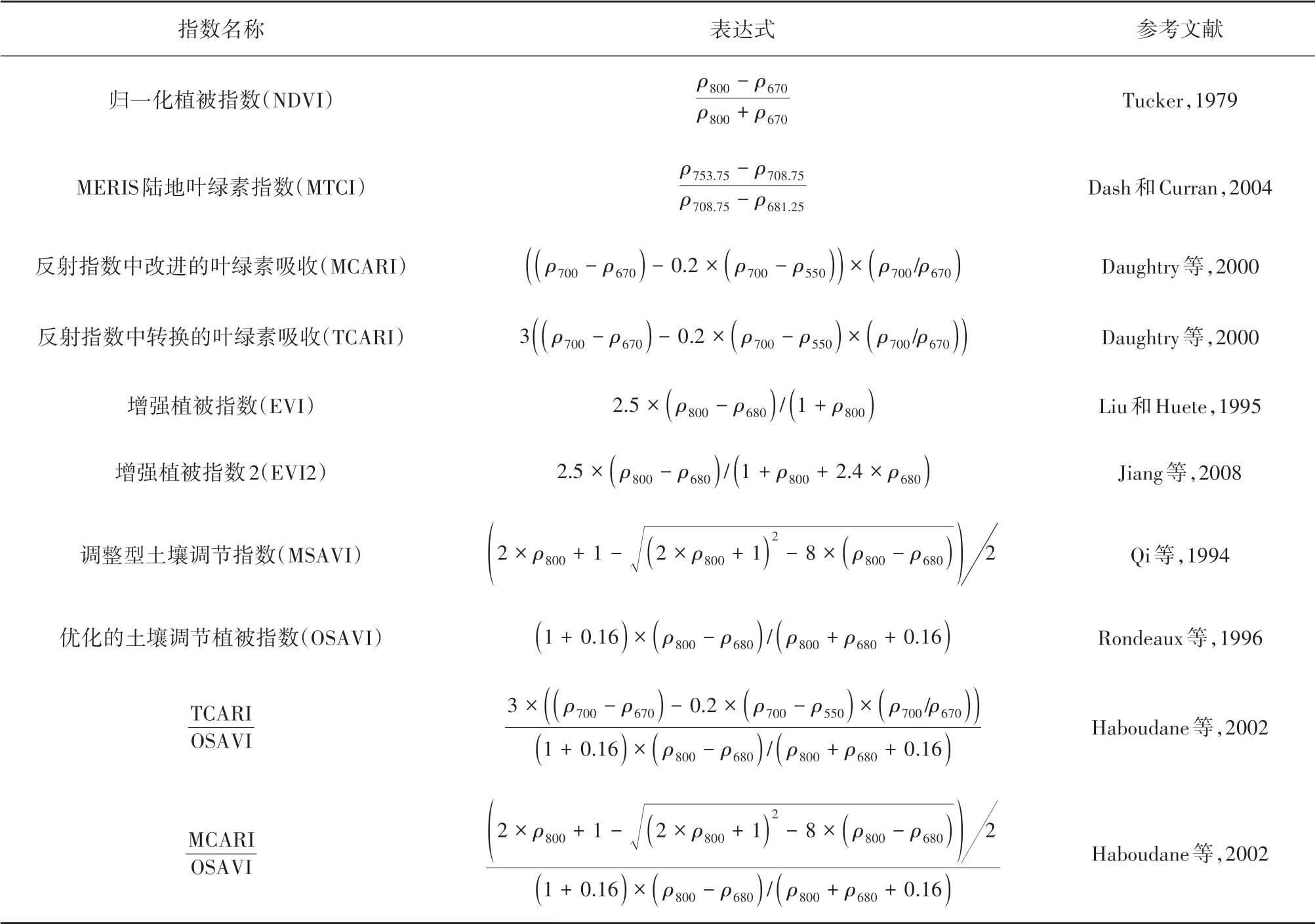
表2 OHS和Sentinel-2A影像传统植被指数的计算Table 2 Calculation of traditional vegetation indices from OHS and Sentinel-2A images

为了获取更为丰富的光谱信息，本文在Tensorflow 2.0 环境下利用Python 3.7 软件的math 标准库分别计算OHS 和Sentinel-2A 数据的组合植被指数（具体计算见式（1）、式（2）和式（3）），主要包括差值光谱指数DSI （Difference Spectral Index）、比值光谱指数RSI（Ratio Spectral Index）和归一化差值植被指数NDSI（Normalized difference spectral index）（Wang等，2017；张亚坤等，2018）。OHS 影像有32 个波段共计算了1488 个组合植被指数；Sentinel-2A数据有12个波段共计算了198个组合植被指数。综合植被指数和组合植被指数，OHS数据一共获得了1498 个特征变量，Sentinel-2A 数据一共得到了208个特征变量。

式中，λ1、λ2是OHS 数据或Sentinel-2A 数据中任意的两个波段，ρλ1、ρλ2分别是λ1、λ2对应两个波段的红树林冠层反射率值。

3.1.2 数据集正态分布检验

本文以7.3∶2.7 的比例随机选取159 个地面实测点作为模型训练数据集，60 个点作为验证数据集，地面实测CCC数据作为目标值（target），植被指数和组合植被指数作为特征变量。本文在Tensorflow 2.0 环境下利用Python 3.7 软件的概率密度函数对特征变量测试集与训练集的进行正态分布检验，OHS 与Sentinel-2A 数据符合正态分布的植被指数以及组合植被指数如图2 和图3所示。OHS 和Sentinel-2A 数据的传统植被指数和组合植被指数均满足正态分布，而OHS 与Sentinel-2A 数据MCARI、TCARI 与MCARI/OSAVI 的训练集与测试集正态分布性相对较差。

图2 OHS数据中符合正态分布的植被指数与组合植被指数Fig.2 Vegetation indices and combining vegetation indices conforming to normal distributions in OHS data

图3 Sentinel-2A数据中符合正态分布的植被指数与组合植被指数Fig.3 Vegetation indices and combining vegetation indices conforming to normal distributions in Sentinel-2A data

3.2 特征降维无量纲化最优数据集生成

3.2.1 最大相关系数法降维

高光谱数据进行植被指数与组合植被指数计算产生了冗余的特征变量，增加了算法的时间复杂度，通过最大相关系数法可以减少冗余信息同时保留与目标值相关性最高的特征变量。在Tensorflow 2.0 环境下利用Python 3.7 软件的Corr 函数绘制热力图，判断特征数据与目标数据的相关性，植被指数与部分组合植被指数的热力图如图4和图5所示。在OHS 与Sentinel-2A 数据中，组合植被指数与红树林CCC 的相关性比植被指数略高。OHS 数据计算的DSI（6，12）与红树林CCC 的相关性最高，Corr 为-0.743。Sentinel-2A 数据相关性最高的指数为NDSI（2，4），Corr 为-0.720。OHS 数据MCARI 指数与目标值的Corr 为0.633 大于0.5，而Sentinel-2A数据的相关系数为0.462，Corr小于0.5。传统植被指数中MTCI、TCARI、TCARI/OSAVI 和MCARI/OSAVI 与目标值的相关性最低，相关系数（Corr）均小于0.5，需要剔除这4 种植被指数。在Tensorflow 2.0 环境下利用Python 3.7 软件feature_selection 库的SelectKBest 类结合相关系数来选择与目标值相关性高的特征变量。经过最大相关系数法降维，OHS 数据由1498 个特征变量减少到11 个，Sentinel-2A 数据由原始的208 个特征变量减少到11个。

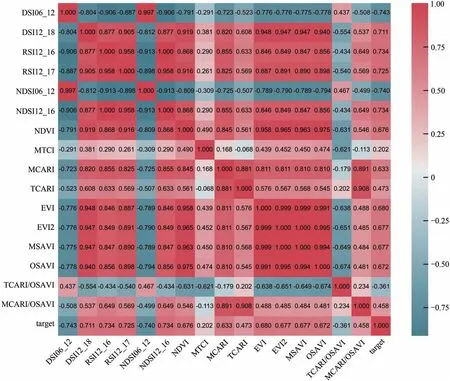
图4 OHS数据特征变量与目标值之间相关性热力图Fig.4 Heat map of correlation between feature variables and target values in OHS data

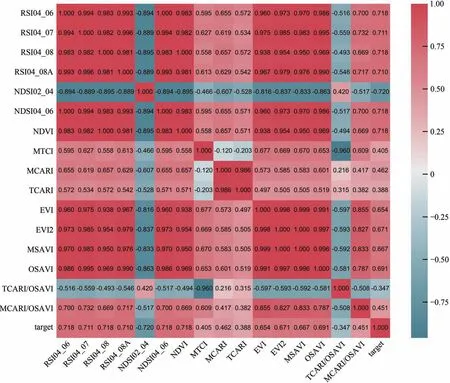
图5 Sentinel-2A数据特征变量与目标值之间相关性热力图Fig.5 Heat map of correlation between feature variables and target values in Sentinel-2A data

3.2.2 基于XGBoost算法的特征选择降维

通过梯度提升算法在红树林CCC 反演方法中获取特征变量的重要性得分，对于重要的特征按重要性得分赋予相应的权重带入到回归器中。通过使损失函数最小化的策略来确定下一棵梯度提升算法的决策树的参数θk，梯度提升算法的表达式见式（4）。

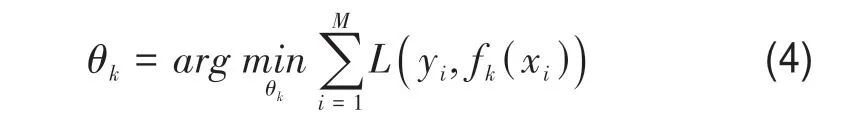
式中，θk为第k个红树林CCC 特征变量基学习器的参数，L(yi，fk(xi))为假设的红树林CCC 特征变量提升树算法的损失函数，M为红树林CCC 特征变量训练集的个数。

将两种数据源最大相关系数法降维后的11 个特征变量输入到极端梯度提升（XGBoost）算法中，在Tensorflow 2.0 环境下利用Python 3.7 软件的feature_importance 函数输出每个特征变量的重要性得分，输出结果如图6 和表3所示。本文经过基于XGBoost 算法的特征选择降维，OHS 和Sentinel-2A数据均得到8个最优特征变量。OHS数据特征变量重要性得分最高的是RSI（12，17），得分为18，NDVI的重要性得分最低，得分为6；Sentinel-2A 数据中特征变量重要性得分最高的是EVI，得分为25，重要性得分最低的是EVI2 与RSI（4，8A），重要性得分均为1 （图6）。说明OHS 数据的RSI（12，17）及Sentinel-2A 数据的EVI 对红树林CCC 更敏感，而OHS 数据的NDVI 与Sentinel-2A 数据的EVI2 和RSI（4，8A）对预测结果的影响较小。

图6 基于XGBoost 算法的特征选择和数据降维结果Fig.6 Feature selection and dimensionality reduction for OHS and Sentinel-2A data using XGBoost algorithm

3.2.3 无量纲化数据集生成

为了消除特征变量与目标值数值之间因数量级不同而产生的不具可比性，本文对特征变量与目标值进行无量纲化。对特征变量进行归一化处理，保留原始数据的特征，提高训练算法的收敛性能；对目标值进行指数转换以提高目标值的正态分布性。对OHS 和Sentinel-2A 数据的8 个最优特征变量及目标值进行无量纲化处理，结果如表3所示。

表3 OHS与Sentinl-2A数据最优特征变量及无量纲化统计结果Table 3 Optimal feature variables and non-dimensional statistical results in OHS and Sentinl-2A data

3.3 红树林CCC反演方法与精度评估指标

为了论证不同回归模型对红树林CCC 反演的适用性，实现红树林CCC 高精度估算。本文利用OHS 和Sentinel-2A 数据无量纲化处理后的8 个最优特征变量及目标值，尝试构建了3种简单一元线性回归模型、4 种单一机器学习回归模型和7 种堆栈集成学习回归模型。

3.3.1 构建红树林CCC反演线性回归模型

线性回归模型反演构建过程中主要涉及模型参数调优，使用的策略是最小化损失函数，线性回归模型的损失函数见式（5），线性回归模型的参数调优问题采用梯度下降法求解，对损失函数求偏导，其表达式见式（6）。

式中，w为各个红树林CCC特征变量特征权重组成的系数向量，b为偏置常数，M为红树林CCC 训练集的个数，h(xi；w；b)是对输入红树林CCC 训练数据xi的预测函数，yi是红树林CCC 训练数据xi的实测值。

本文采用套索算法（Lasso）回归、岭回归（Ridge）及弹性网络（ElasticNet）线性回归模型反演红树林CCC，利用网格搜索方法进行参数调优。经过网格搜索，将Lasso 模型参数正规化项前的常数调节因子（alpha）设置为0.00098；Ridge模型的alpha设为0.25；ElasticNet模型的alpha设为0.0001，最大迭代次数（max_iter）设为100000。

3.3.2 构建红树林CCC反演机器学习回归模型

本文采用KNN 回归模型、RF 回归模型、梯度提升回归树（GBRT）模型和XGBoost 回归模型反演红树林CCC。KNN 回归算法采用K个最近邻多数投票的思想，在给定的距离度量下，最近的K个样本的输出平均值作为回归预测值；RF回归模型、GBRT 回归模型和XGBoost 回归模型均为集成机器学习算法，其中RF 回归模型以决策树为基学习器构建Bagging 集成的基础上，引入随机特征选择构建决策树进行回归预测；GBRT 回归模型是基于Boosting 基学习器的回归算法，利用损失函数的负梯度（梯度下降法）在前项模型的值作为当前提升树算法中残差的近似值，拟合决策树进行回归预测；XGBoost 回归模型是在GBRT 基础上改进而来，在损失函数中增加了正则化项。

机器学习回归模型参数调优的策略是最小化损失函数，机器学习回归模型的优化问题采用梯度下降法求解，分别见式（7）和式（8）。

式中，w为各个红树林CCC最优特征变量特征权重组成的系数向量，b为偏置常数，M为红树林CCC训练数据的个数，f(xi)是建立的模型对红树林CCC测试集的预测函数，yi是红树林CCC训练数据xi的实测值。

利用网格搜索方法确定机器学习回归模型的最优参数，设置KNN 模型的邻近点个数（n_neighbors）为10；设置RF 模型的决策树个数（n_estimators）为250，设置内部节点在划分时所需的最小样本（min_samples_split）为4；设置GBRT模型的n_estimators=150，设置决策树最大深度（max_depth）为1，设置min_samples_split=5；设置XGBoost模型的n_estimators=100，max_depth=1。

3.3.3 构建红树林CCC反演堆栈集成学习回归模型

堆栈集成学习回归模型是采用K折交叉验证单一回归模型并输出预测结果，将每个模型输出的预测结果合并为新的特征（New Feature），并利用新的模型加以训练的回归模型。堆栈集成学习回归模型本质上是一种分层结构，第1 层循环控制基模型的数目，第2层循环控制的是交叉验证的次数K，其原理为：（1）输入7 个单一回归模型，对已有的数据集进行K 折交叉验证；（2）K折交叉验证训练集，对每折输出的结果保存、合并；（3）通过每一次训练模型，对整个测试集进行预测，2 折交叉验证后，将这两列求平均值得到Test1。（4）每一个基模型训练K次，拼接得到预测结果Predictions，最优堆栈集成学习回归模型的结构及原理如图7所示。

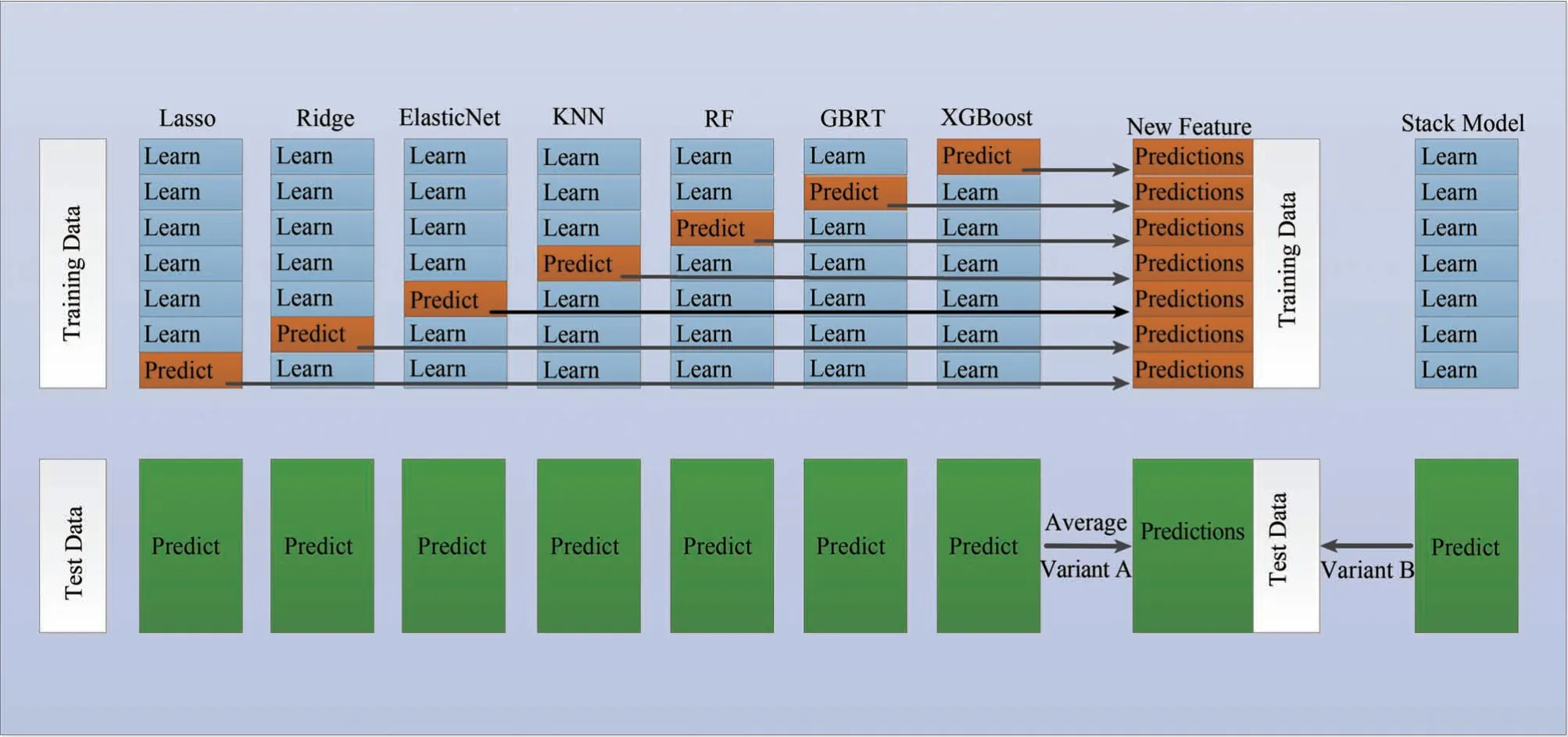
图7 堆栈集成学习回归模型原理结构图Fig.7 Principal structure diagram of stacking ensemble regression model

堆栈集成学习回归的主要过程：（1）利用Python逻辑语句对单一线性回归及机器学习回归算法中模型精度最高的模型结果进行优选；（2）网格搜索后，设置Lasso 回归模型的alpha=0.0001；设置Ridge 模型的alpha=5.75；设置ElasticNet 模型的alpha=0.0009，max_iter=100000；设置KNN模型的n_neighbors=3；设置RF 模型的n_estimators=100，划分考虑最大特征数（max_features）为5，min_samples_split=4；设置GBRT 模型的n_estimators=250，max_depth=2，min_samples_split=7；设置XGBoost模型的n_estimators=100，max_depth=2。

堆栈集成学习回归模型可以集成单一线性回归、机器学习回归模型等许多基础回归模型，产生更稳健的估算结果，在反演过程中提供更好的泛化能力。

利用SNAP 软件神经网络简化的L2 级产品原型处理器SNAP-SL2P （Simplified level2 product prototype processor）算法对Sentinel-2A 数据进行处理，实现LCC 与LAI 的有效估算。SNAP-SL2P算法反演红树林CCC 的过程：（1）进行辐射定标、大气校正与重采样等预处理：（2）利用SNAP 软件下的Biophysical Processor S2 模块生成LAI、LCC两个单波段影像；（3）将LCC 与LAI 两个单波段影像与Sentinel-2A 影像的其他波段进行图层叠加和配准。红树林CCC 反演的技术路线图如图8所示。

3.3.5 精度评估指标

本文为了验证上述3 种反演方法估算红树林CCC 的精度，利用模型得分、均方根误差及决定系数等精度评估指标进行精度估计。

模型得分（Score）可以有效评估不同估算模型预测红树林CCC 的准确率，有助于筛选出预测精度较优的红树林CCC 反演方法，Score 数值在［-1，1］之间（式（9）），Score值越大表示模型的预测精度越高。

式中，n为输入红树林CCC 训练数据集的个数，yi表示红树林CCC 训练集xi的实测值，为测试集xi对应的红树林CCC 反演方法的预测值，为测试集中对应的红树林CCC实测值yi的平均值。

均方根误差（RMSE）可以表征预测值与实测值的曲线的拟合程度，用来衡量模型预测的准确程度，RMSE 值越小，预测精度越高。RMSE 的表达式见式（10）（Inoue等，2016）。

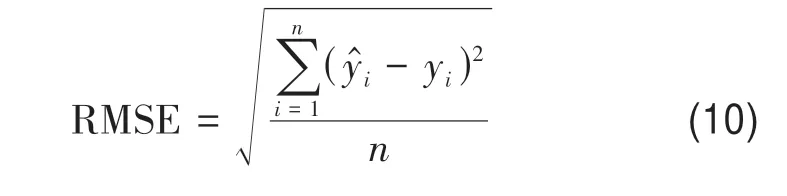
式中，n为输入红树林CCC 训练集或测试集的个数，为红树林CCC 反演方法的预测值，yi为红树林CCC的实测值。

学术立场和观点的分歧源于城市小区治理实践的矛盾，而治理实践的矛盾根源在于，随着中国商品房制度改革以及由此带来的城市小区居住空间结构的变化、社会交往关系的变化、基于物权的权利关系及权利意识的变化等一系列现实和观念的变化，国家对这些变化的认识和制度调整却相对滞后。对小区内部出现的新的经济社会关系及其治理逻辑的辨识，有助于推动当前城市小区治理走出困境。

决定系数（R2）用来表示回归曲线与实测值的拟合程度，R2数值在［0，1］，R2越大表示拟合结果越好。R2的表达式见式（11）（Pham等，2021）。

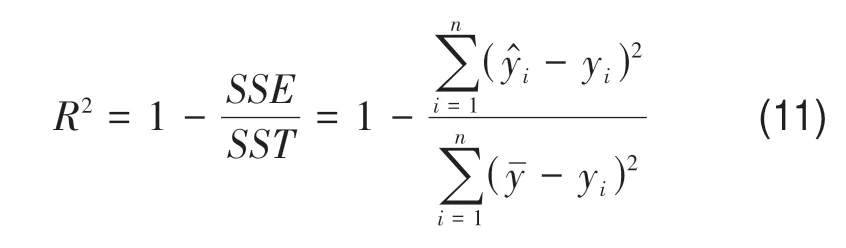
式中，n为输入红树林CCC 测试集的个数，是红树林CCC 反演方法的预测值，yi为红树林CCC 的实测值，为输入红树林CCC测试集的均值。

为了评估各回归模型反演红树林CCC 的性能，模型训练中，从划分的159 个训练集中随机抽取70%（111 个点）作为模型训练的训练数据，其对应的target 数据集中的111 个点作为模型训练的验证数据，利用3 种单一线性回归模型、4 种单一机器学习回归模型及7种堆栈集成学习回归模型对训练数据进行拟合，输出对应训练数据的各回归器拟合曲线上的拟合值，将拟合值与验证数据进行一元线性回归，得到各回归器的Score、RMSE 及Corr精度，通过评估Score、RMSE及Corr值的大小来验证各回归器拟合曲线拟合训练数据的精度。

为了验证不同数据源及不同模型算法反演红树林的CCC 精度，在60 个测试数据中，将基于OHS、Sentinel-2A 数据与最优回归模型输出的预测值、SNAP-SL2P 算法的估算值分别与测试集的目标值进行一元线性回归，利用R2、RMSE 评估其反演精度。

4 精度验证与结果分析

4.1 红树林CCC回归模型训练精度及对比分析

单一线性回归和机器学习回归模型训练中（训练结果见表4），除了KNN 模型预测精度较低，基于CART的强机器学习回归器精度明显优于线性回归器的精度。OHS 数据中，最优线性回归模型为Lasso回归器，Score为0.612（图9（a）），RMSE为20.346 μg/cm2，Corr 为0.783，最优的机器学习回归模型是RF 回归器，Score 为0.932，RMSE 为8.494 μg/cm2，Corr为0.971（图10（c））；最优机器学习回归器比最优线性回归器的Score提高了0.320，RMSE 降低了11.852 μg/cm2，Corr 提高了0.188。Sentinel-2A 数据中，最优机器学习回归模型是RF回归器，Score 为0.884，RMSE 为11.148 μg/cm2，Corr 为0.943（图10（d）），而最优线性回归模型是ElasticNet 回归器，Score 为0.651，RMSE 为19.316 μg/cm2，Corr 为0.807（图9（f））；最优RF机器学习回归器比最优ElasticNet 线性回归器的Score 提高了0.233，RMSE 降低了8.168 μg/cm2，Corr 提高了0.136。说明单一线性回归和机器学习回归模型训练中，RF 回归模型是训练精度最高的红树林CCC反演模型。

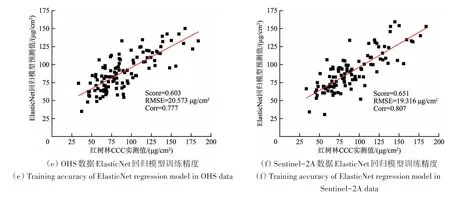
图9 OHS与Sentinel-2A数据单一线性回归模训练精度Fig.9 Training accuracy of single linear regression models in OHS and Sentinel-2A data

图10 OHS与Sentinel-2A数据单一机器学习回归模型精度Fig.10 Training accuracy of single machine learning regression models in OHS and Sentinel-2A data

表4 OHS与Sentinel-2A数据单一线性回归和机器学习回归模型训练精度Table 4 Training accuracy of single linear regression and machine learning regression models in OHS and Sentinel-2A data

堆栈集成学习回归结果中（预测结果见表5），OHS数据最优堆栈集成学习回归模型是GBRT回归器，Score 为0.999，RMSE 为0.963 μg/cm2，Corr 为0.999（图12（e））；3 种堆栈线性集成学习回归器精度趋于一致，其中Ridge 回归器Score 为0.981，RMSE 为4.445 μg/cm2，Corr 为0.991（图11（c））；最优堆栈GBRT 集成学习回归模型比最优堆栈Ridge 线性回归模型的Score 提高了0.018，RMSE降低了3.482 μg/cm2，Corr 提高了0.008。Sentinel-2A 数据的最优堆栈集成学习回归模型是XGBoost回归器，Score 为0.991，RMSE 为3.012 μg/cm2，Corr 为0.996（图12（h））；3 种线性回归模型精度趋于一致，其中Ridge 的Score 为0.944，RMSE 为7.748 μg/cm2，Corr 为0.971（图11（d））；XGBoost回归器比Ridge 回归器的Score 提高了0.047，RMSE降低了4.736 μg/cm2，Corr提高了0.025。

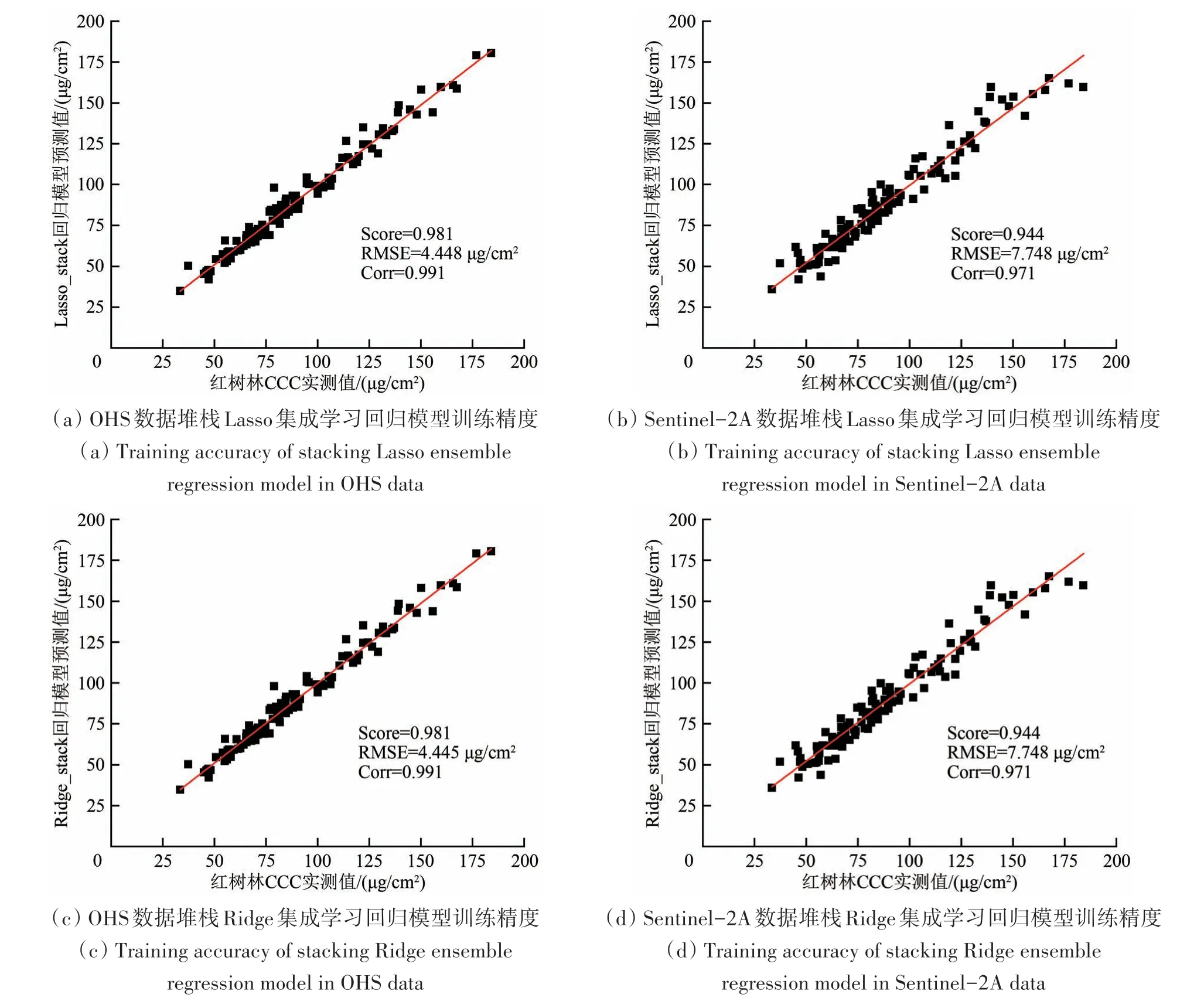
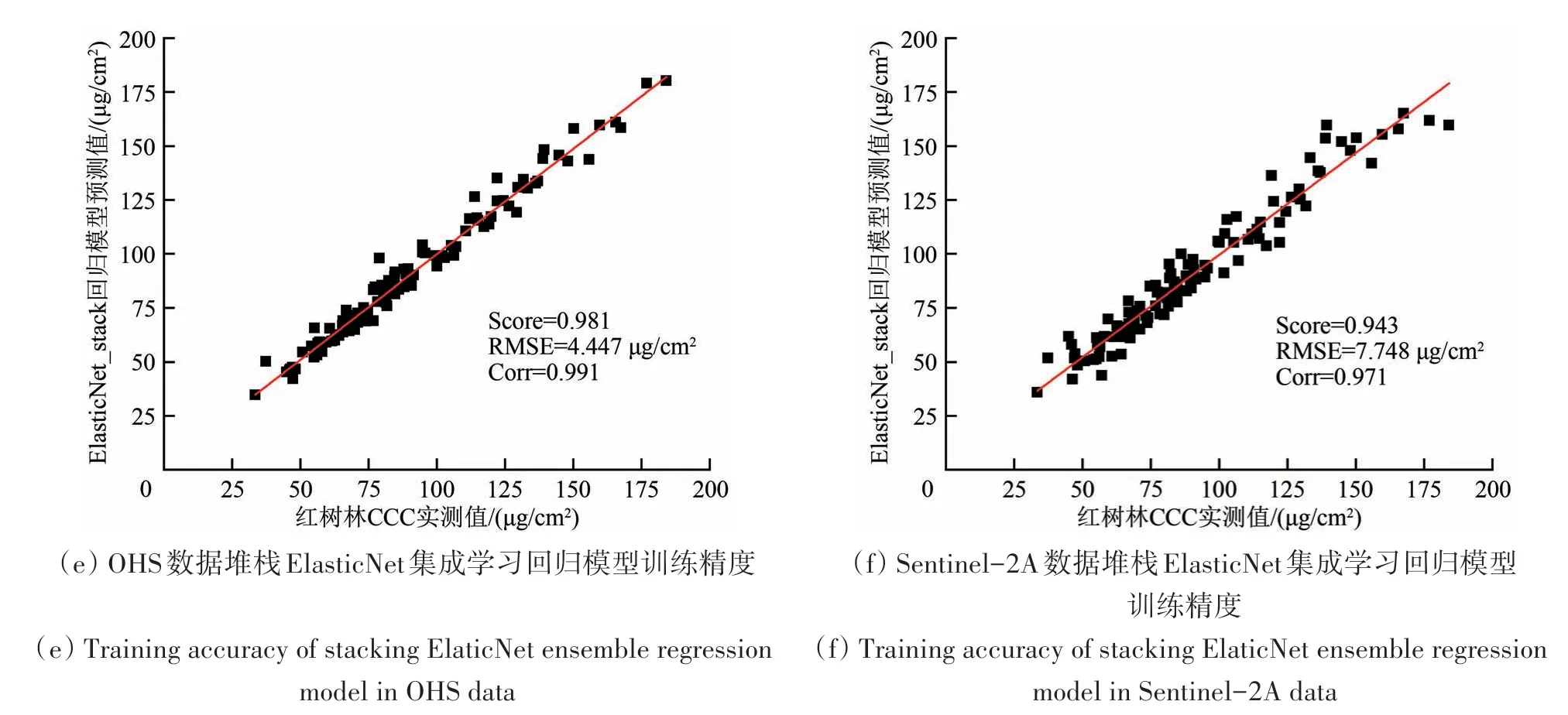
图11 OHS与Sentinel-2A数据堆栈线性回归模型训练精度Fig.11 Training accuracy of stacking linear regression models in OHS and Sentinel-2A data

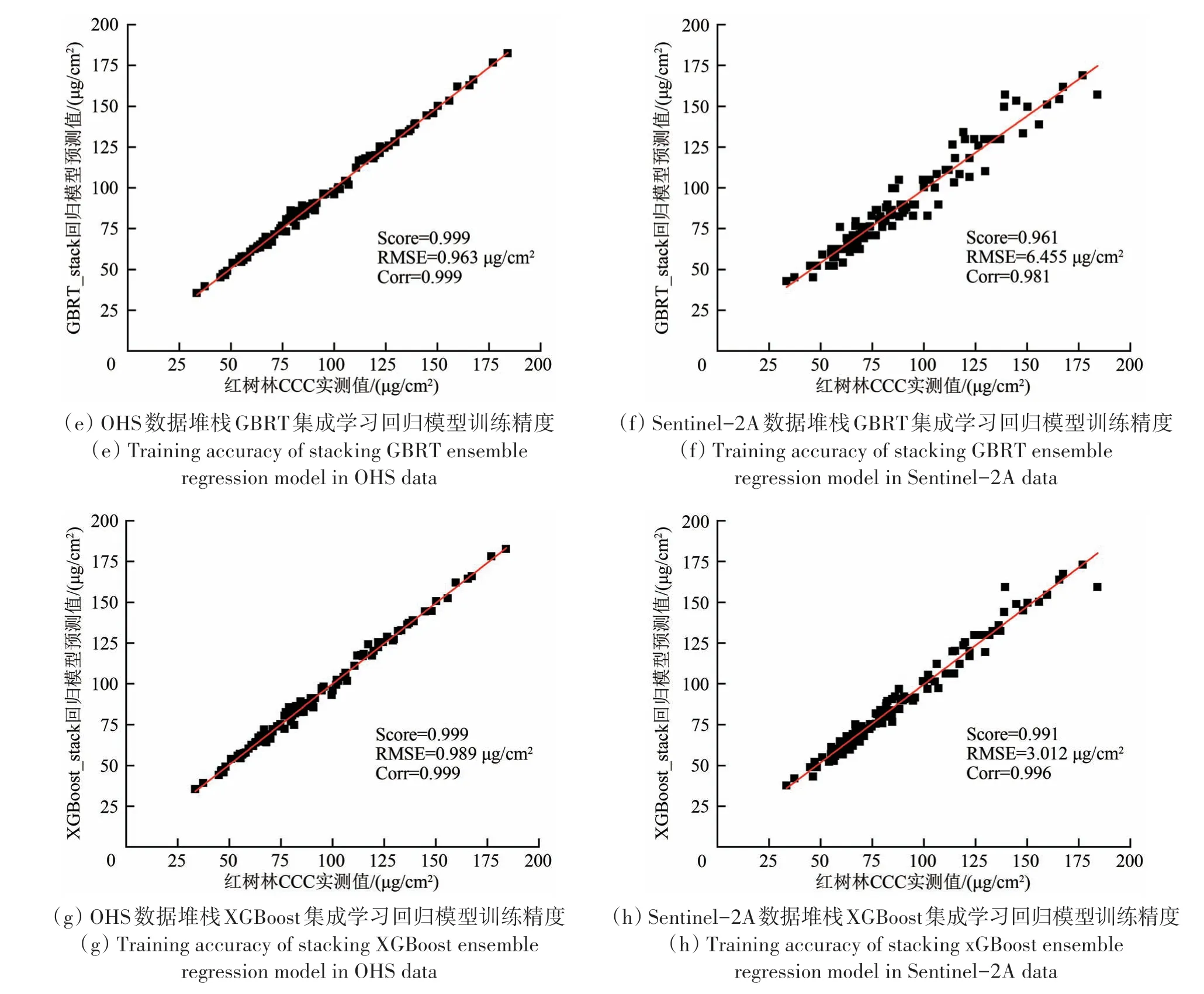
图12 OHS与Sentinel-2A数据堆栈机器学习回归模型训练精度Fig.12 Training accuracy of stacking machine learning regression models in OHS and Sentinel-2A data

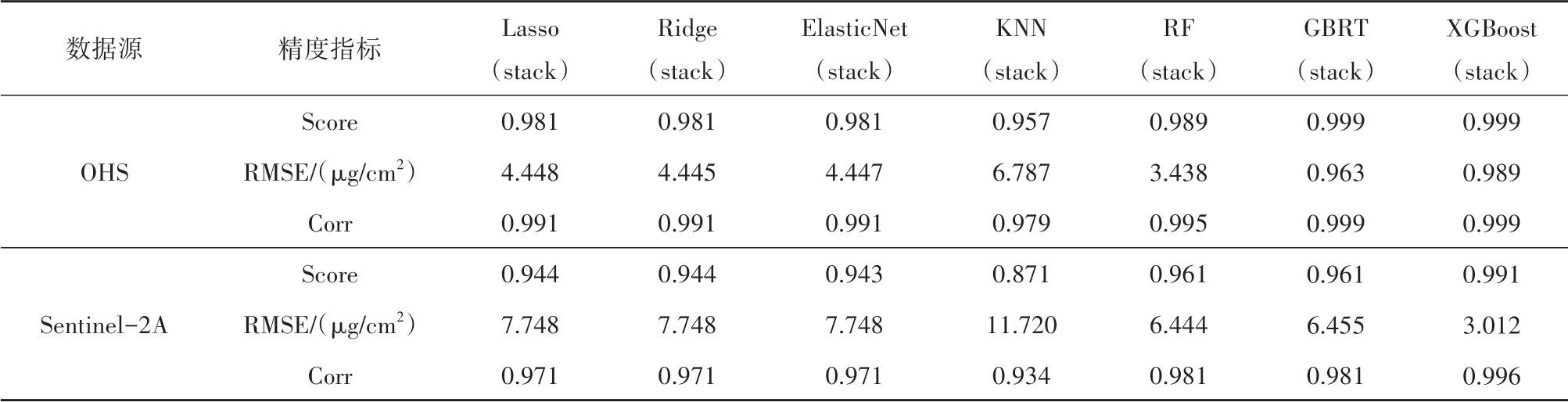
表5 OHS与Sentinel-2A数据堆栈集成学习回归模型训练精度Table 5 Training accuracy of stacking ensemble regression models in OHS and Sentinel-2A data

OHS 数据拥有比Sentinel-2A 数据更丰富的波段，其特征数据集复杂程度更高，在单一线性回归模型训练中，Sentinel-2A 数据最优ElasticNet 线性回归模型比OHS 数据最优Lasso 线性回归模型的精度略高（RMSE 降低了0.985 μg/cm2），这是因为单一线性回归模型对于数据复杂的数据集难以建模。单一线性回归和机器学习回归模型训练中输入数据是非线性和特征间具有相关性的数据集，RF 回归模型具有较高的集成能力，对于复杂的数据集，RF 模型的拟合曲线较好地拟合了红树林CCC 实测值，相比之下，线性回归模型的拟合能力较弱。在堆栈集成学习回归模型中，线性回归模型在预测过程中出现了精度饱和的情况，而堆栈GBRT 及XGBoost 集成学习回归模型有效避免了过拟合的情况，具有更强的泛化能力，并在单一最优机器学习回归模型训练中得到较优结果的基础上再一次提升了红树林CCC的估算精度。

堆栈集成学习回归前后的两次模型训练，机器学习回归模型对数据的拟合程度都比线性回归高，说明机器学习回归模型在反演红树林CCC 的性能明显优于线性回归模型；相较于单一最优线性和最优机器学习回归模型，堆栈集成学习回归模型集成了单一线性回归、机器学习回归模型的优势，反演红树林CCC的精度最高。

4.2 OHS 与Sentinel-2A 数据红树林CCC 估算精度与结果分析

在单一机器学习回归模型训练过程中，基于OHS 数据的最优RF 回归器的Score 比基于Sentinel-2A 数据的最优RF 回归器高0.048，RMSE降低了2.654 μg/cm2，Corr提高了0.028（图13（a），图13（b））；而在堆栈集成学习回归模型中，基于OHS数据的最优GBRT 模型的RMSE 比基于Sentinel-2A数据的最优XGBoost 模型降低了2.049 μg/cm2（图13（c），图13（d））。说明OHS 数据为最优堆栈集成学习回归算法提供了最优的拟合数据集，OHS 数据的RSI（12，17）、DSI（12，18）和NDSI（6，12）组合植被指数对红树林CCC的敏感性较高。

图13 OHS与Sentinel-2A数据反演红树林CCC训练精度对比Fig.13 Comparison of inversing training accuracy of mangrove CCC between OHS and Sentinel-2A data

本文选取了60 个测试集的目标数据验证OHS与Sentinel-2A 数据反演红树林CCC 的精度（验证结果见表6）。通过一元线性拟合，得到联合OHS数据与最优堆栈GBRT 集成学习回归的R2为0.761，RMSE为16.738 μg/cm2（图14（a））；联合Sentinel-2A数据与最优堆栈XGBoost集成学习回归模型的R2为0.615，RMSE 为20.701 μg/cm2（图14（b））；联合OHS 数据和最优堆栈集成学习回归模型的红树林CCC 反演精度最高，比Sentinel-2A 数据的R2高0.146，RMSE 降低了3.963 μg/cm2。说明基于OHS、Sentinel-2A 数据与最优堆栈集成学习回归模型都能有效反演红树林CCC，而在最优堆栈集成学习回归模型下，OHS 数据比Sentinel-2A 数据的预测精度更高。基于OHS、Sentinel-2A 数据与最优堆栈集成学习回归模型预测值之间的R2>0.7、RMSE<14 μg/cm2和Corr>0.8（图14（f）），说明两种数据源的预测值之间具有很高的相关性。

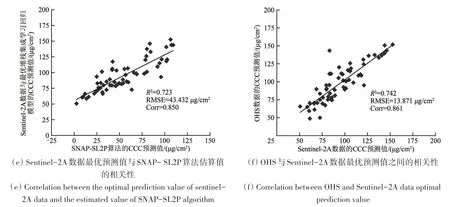
图14 基于多源数据和最优反演模型的红树林CCC精度对比Fig.14 Comparison of inversing accuracy of mangrove CCC between OHS and sentinel-2A data using optimal models

联合OHS、Sentinel-2A 数据与最优堆栈集成学习回归模型都实现了红树林CCC 的有效估算，将两种数据源分别与最优堆栈集成学习回归模型输出的预测值与红树林CCC 验证数据集构建一元线性拟合回归方程，见式（12）和式（13）。

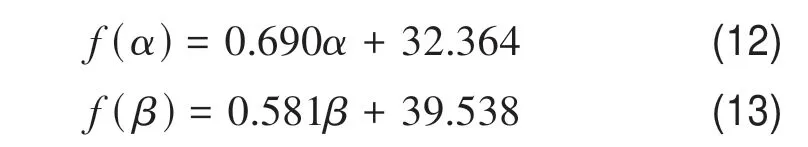
式中，f(α)、f(β)是分别联合OHS、Sentinel-2A数据与最优堆栈集成学习回归模型得到的回归方程，α、β是分别联合OHS、Sentinel-2A 数据与最优堆栈集成学习回归模型输出的预测值。

4.3 最优红树林CCC 反演模型与SNAP-SL2P 算法精度验证与结果分析

本文利用60 个红树林CCC 验证数据集评估分别基于OHS、Sentinel-2A 数据与最优堆栈集成学习回归模型、SNAP-SL2P 算法反演红树林CCC 的精度（验证结果见表6）。SNAP-SL2P 算法估计红树林CCC 的R2为0.356，RMSE 为49.419 μg/cm2（图14（c））；基于OHS 数据的最优堆栈GBRT 集成学习回归模型比SNAP-SL2P 算法反演红树林CCC 的R2高0.405，RMSE 降低了32.681 μg/cm2；而在相同Sentinel-2A数据源下，最优堆栈XGBoost集成学习回归模型对比SNAP-SL2P 算法的R2提高了0.259，RMSE 降低了28.718 μg/cm2；SNAP-SL2P算法反演红树林CCC 的精度最低，R2小于0.4，RMSE大于40 μg/cm2，说明最优堆栈集成学习回归模型比SNAP-SL2P 算法在反演红树林CCC 中更具有可靠性。SNAP-SL2P算法在估算红树林CCC时，存在明显的系统低估，尤其在估计LAI时，SNAPSL2P 算法估算的LAI 均值（1.226）比实测值（2.014）低估了近一倍。环境因素会对SNAP-SL2P算法中PROSAIL 模拟的冠层反射率值造成一定程度的影响，而由OHS 数据计算的最优特征变量有效避免了红树林地区土壤、海区污染物和海水等环境因子的影响。

表6 基于多源数据和不同回归模型的红树林CCC反演精度对比分析Table 6 Comparison of inversing accuracy of mangrove CCC between different regression models and multi-sources data

本文对3种红树林CCC反演方法的预测值进行了回归分析（图14），联合OHS数据和最优堆栈集成学习回归模型的预测值与SNAP-SL2P 算法的估算值R2为0.501，RMSE 为48.734 μg/cm2，相关系数Corr 为0.708（图14（d））；联合Sentinel-2A 数据和最优堆栈集成学习回归模型的预测值与SNAP-SL2P 算法的估算值R2为0.723，RMSE 为43.432 μg/cm2，Corr 为0.850（图14（e））。SNAPSL2P 算法估算值与分别基于OHS、Sentinel-2A 数据的最优堆栈集成学习回归模型预测值之间的Corr均大于0.7，说明3 种反演方法的预测值之间具有较高的相关性。虽然在相同的Sentinel-2A 数据源下，最优堆栈集成学习回归模型预测值与SNAPSL2P 算法估算值间有着较高的Corr（>0.8）和R2（>0.7），但是SNAP-SL2P 算法的RMSE 大于43 μg/cm2，说明SNAP-SL2P 算法在红树林CCC 反演中存在明显的系统性低估。联合OHS 数据和最优堆栈集成学习回归模型的预测值与SNAP-SL2P算法的估算值的R2（<0.6）、RMSE（>48 μg/cm2）和Corr（<0.8）最低，这是由于两者的数据源和算法之间都存在差异性，说明基于OHS 数据的最优堆栈集成学习回归模型、SNAP-SL2P 算法不能同时有效反演红树林CCC。

SNAP-SL2P 算法在红树林CCC 反演中出现了明显的系统性低估。在研究区上，利用SNAPSL2P 算法绘制的LAI、LCC 专题图（图15）可以有效刻画研究区红树林LAI和LCC的空间分布，有助于监测红树林健康状况。苏屋村分布的树种主要是白骨壤，研究区中间的河道附近的红树林LAI及LCC较高，而道路沿岸的红树林LAI与LCC较低（图15（a），图15（c））。沙角村主要分布着白骨壤、桐花树和秋茄，研究区域内高纬度地区主要分布着秋茄与桐花树，而相对低纬度地区主要分布着白骨壤与秋茄（图15（b），图15（d））。高纬度地区的LAI与LCC值比低纬度的高，与该地区桐花树的分布面积较大有关。

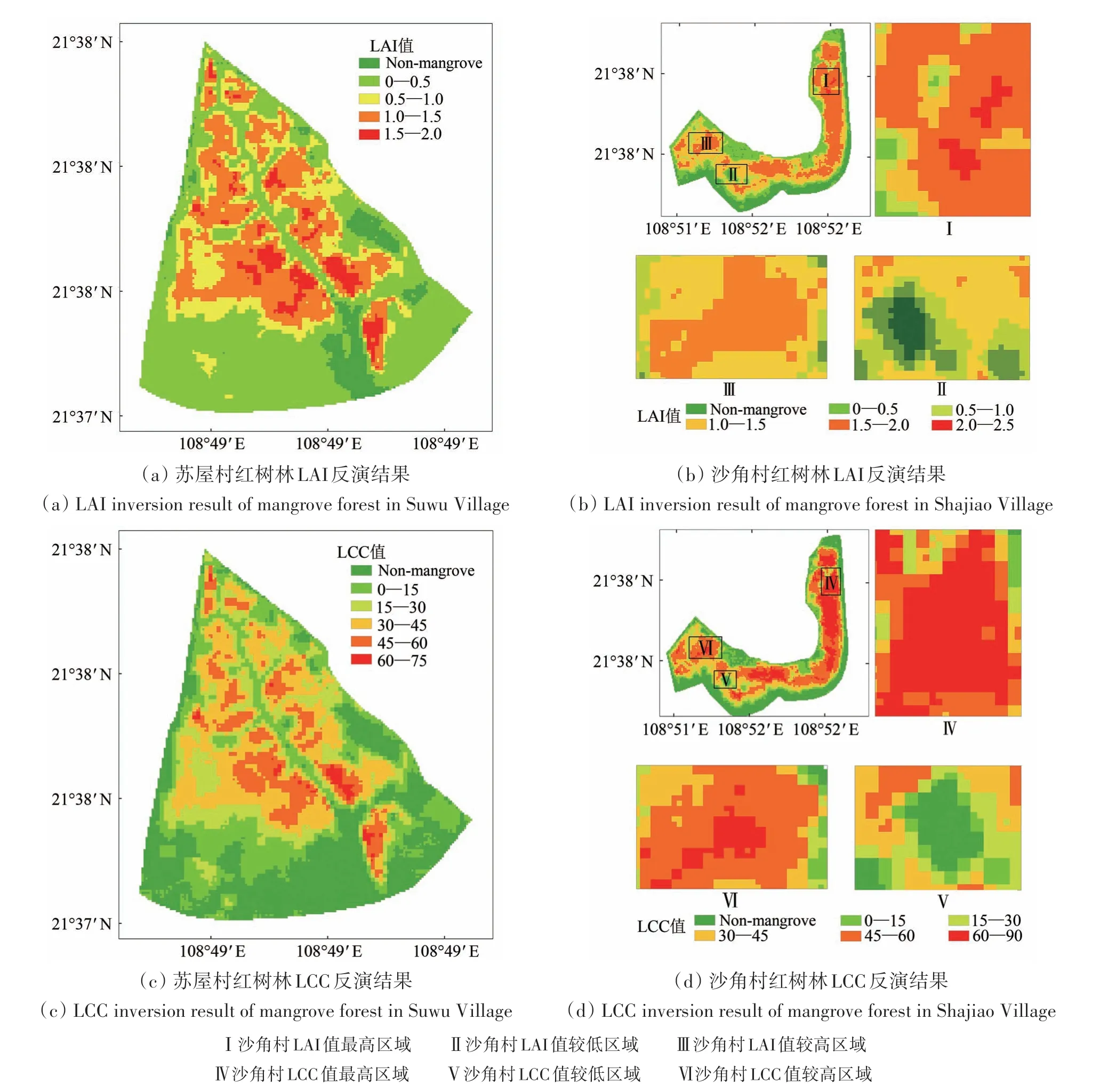
图15 基于SNAP-SL2P算法提取的研究区红树林LAI及LCC值Fig.15 LAI and LCC value of mangrove calculated by SNAP-SL2P algorithm

5 结论

本文以OHS 和Sentinel-2A 为数据源，通过数据降维和变量优选，构建了最优堆栈集成学习回归模型，实现了北部湾红树林CCC 的高精度反演，得出以下结论：

（1）实现了正态分布检验、最大相关系数法和基于XGBoost 算法的特征选择方法对OHS 数据1498 个高维数据集进行特征降维和变量优选，优选出8 个最优特征变量，其中RSI（12，17）、DSI（12，18）和NDSI（6，12）组合植被指数对红树林CCC 的敏感性较高；

（2）对比了单一线性回归和机器学习回归模型与堆栈集成学习回归模型的训练精度，OHS数据最优堆栈GBRT 集成学习回归模型（Score=0.999，RMSE=0.963 μg/cm2，Corr=0.999），比最优机器学习RF 回归器的RMSE 降低了7.531 μg/cm2，比最优线性Lasso 回归器的RMSE 降低了19.383 μg/cm2，堆栈集成学习回归模型是训练精度最高的反演模型；

（3）对比了OHS 和Sentinel-2A 数据反演红树林CCC 的精度，OHS 数据（R2=0.761，RMSE=16.738 μg/cm2）比Sentinel-2A 数据（R2=0.615，RMSE=20.701 μg/cm2）的R2提高0.146，RMSE 降低了3.963 μg/cm2，OHS 数据是反演红树林CCC 的最佳数据源；

（4）对比了最优堆栈集成学习回归模型与SNAP-SL2P算法估算红树林CCC的精度，基于OHS、Sentinel-2A 数据的最优堆栈集成学习回归模型比SNAP-SL2P 算法（R2=0.356，RMSE=49.419 μg/cm2）的R2分别提高了0.405 和0.259，RMSE 降低了32.681 μg/cm2和28.718 μg/cm2，堆栈集成学习回归模型是红树林CCC估算中精度最优的反演模型。

本文在红树林CCC 最优反演模型和最佳数据源的选择上进行了系统性的研究，但是仍需要进一步改进：在红树林最优反演模型和最优数据集的构建过程中，下一步将采用深度学习回归模型，实现CCC 的高精度智能估算；下一步将采用高空间分辨率的无人机、多光谱和高光谱数据实现红树林种群的CCC反演。

志 谢此次实验的高光谱卫星影像采用了珠海欧比特宇航科技股份有限公司的珠海一号高光谱卫星数据产品，在此表示衷心的感谢！