各向异性介质空间-波数混合域直流电阻率法三维数值模拟研究

戴世坤， 凌嘉宣*， 陈轻蕊， 张莹， 李昆

1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室， 长沙 410083 2 中南大学有色资源与地质灾害探查湖南省重点实验室， 长沙 410083 3 中南大学地球科学与信息物理学院， 长沙 410083 4 西南石油大学地球科学与技术学院， 成都 610500

0 引言

直流电阻率法作为地球物理勘探中较为成熟的方法，被广泛应用(Ren et al., 2018a)，但其在数值模拟研究中，由于场源奇异性、大差异电导率对比、复杂几何结构、非均匀性、各向异性和大尺度规模等问题对算法和计算机体系结构提出了更高的要求，为了解决这些问题，多年来很多学者进行了探索(Wait，1990；Al Hagrey，1994；阮百尧和熊彬，2002；熊彬和阮百尧，2002；Li and Spitzer，2002；沈松金和郭乃川，2008；沈松金等，2009；陈桂波等，2009；王威和吴小平，2010；王威，2013；Wang et al.，2013；Yin et al.，2016；Ren et al.，2018b；殷长春等，2018；张钱江等，2016；任政勇等，2018).目前，针对地下介质为各向异性结构的直流电阻率法数值方法研究包括积分方程法(Eskola and Hongisto，1981，1997；Eskola，1988，1992；Eloranta，1988；Flykt et al.，1996；Li and Uren，1997；陈桂波等，2009)，有限差分法(Dey and Morrison，1979；Lowry et al.，1989；Spitzer，1995；Zhao and Yedlin，1996；Wang and Fang，2001；Hou et al.，2006；Chen et al.，2017)，有限单元法(Coggon，1971；Bibby，1978；Pridmore et al.，1981；徐世浙，1988；Zhou and Greenhalgh， 2001; Zhou et al.，2009；熊彬和阮百尧，2002；Li and Spitzer，2002，2005；王威和吴小平，2010；王威，2013；Wang et al.，2013；Yan et al.，2016；Yang et al.，2018；任政勇等，2018).相对于其他两种方法，有限单元法因有完善的理论和可用非结构化网格剖分的特性，更适合模拟地形和地下复杂结构介质，因此被深入研究和广泛应用，这为解决复杂各向异性介质模型下三维数值模拟问题提供巨大动力(Wang et al.，2013).为了探索和分析地下各向异性介质的特性，近年来部分学者采用基于有限单元法的直流电阻率法对地下三维各向异性介质进行了研究.Li 和 Spitzer(2005)推导了各向异性下基于总场和二次场的边值条件，并利用混合边界条件实现了地下介质为不同各向异性形态的三维数值模拟；Zhou等(2009)利用基于“Gaussian quadrature grid”方法的有限单元法实现各向异性介质的响应计算，该方法不需要与表面地形匹配的恒定单元的网格就取得较好的效果；王威和吴小平(2010)利用二次场方法和SSOR预条件共轭梯度算法实现了电阻率任意三维各向异性模型的地电响应；Wang等(2011, 2013)采用非结构化网格有限单元法实现了任意各向异性三维直流电阻率法的三维数值模拟；Yang等(2018)采用非结构化网格自适应有限单元法模拟任意各向异性介质的响应，该方法采用基于梯度恢复理论的局部自适应网格细化技术，结合圆形扫描直流测量技术，获得了更多关于地球不同深度的电阻率和电各向异性特性的信息.Ren等(2018c)在考虑地形和各向异性介质条件下，利用面向目标的自适应有限单元法实现了三维直流电法的数值模拟.

前人关于直流电阻率法三维有限单元法的数值模拟研究中，大都直接在空间域中将三维模型进行剖分，然后求解满足边值问题的大型方程组，这样求解方程组占用内存大，计算时间较长.本文采用一种空间波数混合域方法对直流电阻率法进行三维数值模拟，具体为对异常电位满足的微偏微分方程沿水平方向进行二维傅里叶变换，令水平方向转换成波数域，保留垂直方向为空间域，由此可根据地下介质电流密度变化快慢灵活剖分网格(电流密度变化剧烈区域采用稠密剖分方式，电流密度变化缓慢区域采用稀疏剖分方式).这样将空间域异常电位满足的三维偏微分方程转化成不同波数满足的一维常微分方程，把一个大规模三维数值模拟问题分解为多个一维数值模拟问题，并在空间波数混合域中利用一维有限单元法求解方程组，大大减小内存使用量和计算时间.利用压缩算子进行迭代，最后获得高精度近似解.该方法通过利用二维傅里叶的快速性和追赶法(Boisvert, 1991)求解常微分方程的高效性，实现了直流电阻率法三维数值模拟，这为研究和分析地下介质各向异性特性提供一种新途径.

1 方法原理

1.1 控制方程

将点电源置于各向异性介质中，可得电位满足的微分方程(徐世浙，1994)

(1)

(2)

(3)

其中

(4)

矩阵D是与三个欧拉角有关的变换矩阵，具体表达式为

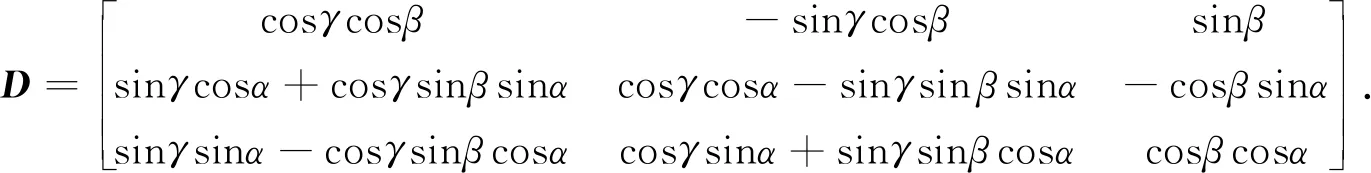
(5)

(6)

根据叠加原理，总电位U可以分解为

U=Ua+Ub,(7)

将式(6)和式(7)代入式(1)，可得

-2Iδ(r-r0),(8)

正常电位Ub满足

(9)

将式(9)代入式(8)并整理，得到异常电位Ua满足的微分方程为

(10)

散射密度ja满足

(11)

式中E为总电场，式(10)可表示为

(12)

(12)式即为各向异性介质空间域异常电位Ua满足的控制方程.将式(12)展开，可得

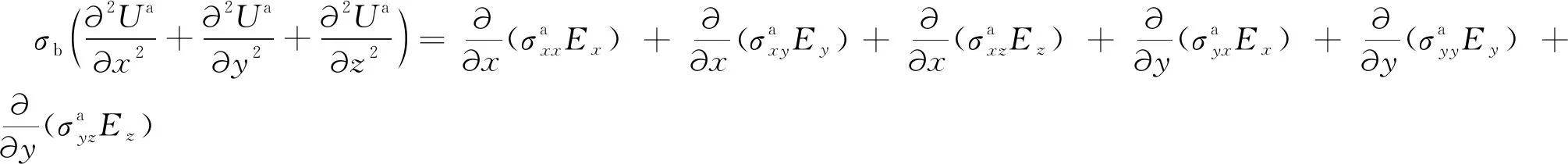
(13)

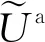
(14)

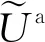
(1)令总电场E(0)的初始值等于背景电场；

(3)对波数域异常电场和电位进行二维傅里叶变换得到空间域异常电场和异常电位，然后计算总电场和总电位；

(4)引入压缩算子对总电场进行修改，得到新的总电场E(1)；

(5)判断前后两次总电场的相对残差是否满足期望的数值精度.若满足精度要求，输出结果，否则取E(0)=E(1)，重复步骤(2)—(5)，直至满足收敛条件.

1.2 边界条件

为了确定控制方程式(14)的定解问题，还需给出z向上合适的边界条件.设边界区域如图1所示，在笛卡儿坐标系下，令z轴垂直向下为正方向，计算区域取水平地面为上边界zmin，取地下离异常体一定远处为下边界zmax.

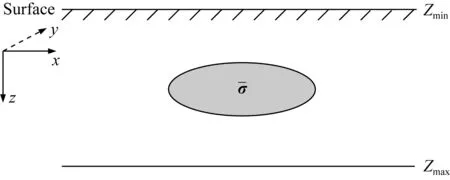
图1 边界条件示意图Fig.1 Schematic diagram of boundary conditions

对于上边界zmin，空气与地下介质的分界面满足电位法向为零，由此，上边界zmin处电位满足

(15)

下边界zmax离异常体一定距离，ja在下边界处为零，由式(14)可得

(16)

该方程的通解为

(17)

因二次电位在下边界只存在下行波e-kx，则有

(18)

对上式求导，可得

(19)

联立式(15)和式(19)获得控制方程式(14)的边界条件：

(20)

1.3 边值问题

综上所述，各向异性介质的空间-波数混合域异常电位满足的边值问题为

(21)

式(21)将各向异性介质空间域异常电位满足的三维偏微分方程转化成不同波数满足的一维常微分方程，由此大大减少了计算量以及对存储的需求.因不同波数之间的常微分方程相互独立，故分别使用有限单元法求解，并利用追赶法求解定带宽线性方程组.

1.4 常微分方程求解

该方法保留垂直方向在空间域，这样可以根据地下异常区域电流密度变化快慢灵活剖分，可准确模拟地下异常区域.对于异常电位在空间-波数混合域中满足的常微分方程式(21)，本文采用基于二次插值的一维有限单元法进行求解.基于变分原理(徐世浙,1994)，边值问题式(21)等价变分问题为

在图1中沿z向进行单元剖分，每个单元的异常电位和电流密度采用节点二次插值函数表示.通过离散，对(22)式逐项单元分析、总体合成，得到扩展矩阵或列阵：

(23)

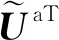
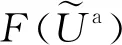
(24)

(25)

式中，Ka是五对角矩阵，Pa是源项.

对于该五对角线性方程组，采用追赶法求解，通过空间波数混合域电场与电位的关系式(28)易得空间-波数混合域异常电场，然后使用标准FFT法(Tontini et al.，2009)对空间-波数混合域的电场进行反傅里叶变换，得到空间域异常电场.再将背景电场加上异常电场得到总电场，并采用压缩算子迭代计算获得空间域中修改的总电场.

1.5 压缩算子

只有当异常体电导率与背景介质电导率之间差异较小时，求解式(25)才能得到较为准确的解(Berdichevsky and Zhdanov, 1984)，通常地下介质电导率差异较大(≥101)，此时求解式(25)得到的数值解与正确解差异很大，为此，Zhdanov和Fang(1996)和Gao(2005)在求基于积分方程的解时提出了一种迭代算子，鉴于三维直流电法积分解和微分解的等效性，将该迭代算子引入基于微分解的三维直流电法数值模拟当中，该迭代算子的表达式为

(26)

式中，α、β均为张量，E(n-1)表示第n-1次求解式得到的总电场，E(n)′表示第n次迭代计算得到的总电场，E(n)表示采用压缩算子修改后得到的第n次迭代的总电场.算法的步骤为：

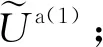
(3)将背景电场Eb加上异常电场Ea(1)′得到总电场E(1)′；

(4)利用压缩算子式(26)得到修正后的总电场E(1)；

(5)判断修改前后总电场的相对残差abs(E(1)-E(0))/abs(E(0))是否满足期望的数值精度ε0，即abs(E(1)-E(0))/abs(E(0))<ε0.若满足精度要求，输出结果，否则取E(0)=E(1)，重复步骤(2)—(5)，直至满足收敛条件.

1.6 异常电场的计算

因使用压缩算子迭代时需要求出电场，由式(11)可知各向异性介质空间-波数混合域的异常电场分量与异常电位的关系式为

(27)

1.7 零波数处理

在空间波数域中求解得电场后，采用标准FFT法进行反傅里叶变换时，需对波数k(kx,ky)为零的情况进行处理，否则会影响计算精度，造成较大误差.当波数kx,ky均为零时，异常电场的表达式为

(28)

2 算例及分析

算例均采用Fortran语言编写的各向异性介质空间-波数混合域三维直流电阻率数值模拟程序测试，测试平台配置为Inter(R) Core(TM) i3-4150 CPU，@3.50 GHz(4核)，16 GB RAM.

2.1 算法正确性验证

为了验证本文算法的准确性和计算精度，对各向同性半空间存在各向异性棱柱异常体模型1(如图2所示)进行数值计算，计算结果与自适应有限单元法(Ren et al.，2018c)对比.该模型的计算区域为200 m×200 m×81 m，背景电阻率为100 Ωm，异常体相关参数如下：顶部埋深为10 m，大小为12 m×12 m×10 m，三个电阻率主分量为ρ1/ρ2/ρ3=10/5/2 Ωm，对应欧拉角为α/β/γ=30°/45°/60°.异常体中心位置在地面上的投影位于原点坐标.采用均匀网格进行剖分，网格大小为1 m.采用二极装置测量，供电电极位于原点坐标，电流大小为1 A.在使用本文算法计算时，使用标准FFT法进行傅里叶变换，为了减小截断效应带来的误差影响，分别沿x和y轴方向向外扩边不同距离(0 m，20 m，40 m，80 m)进行计算.图3表示本文算法和自适应有限单元法在地面上分别沿x轴方向测量得到的视电阻率曲线图及相对误差图，从图中可看出本文算法与自适应有限单元法的相对误差小于1%，验证了本文算法的准确性.同时也说明了本文算法的精度随着扩边距离的增加而提高.

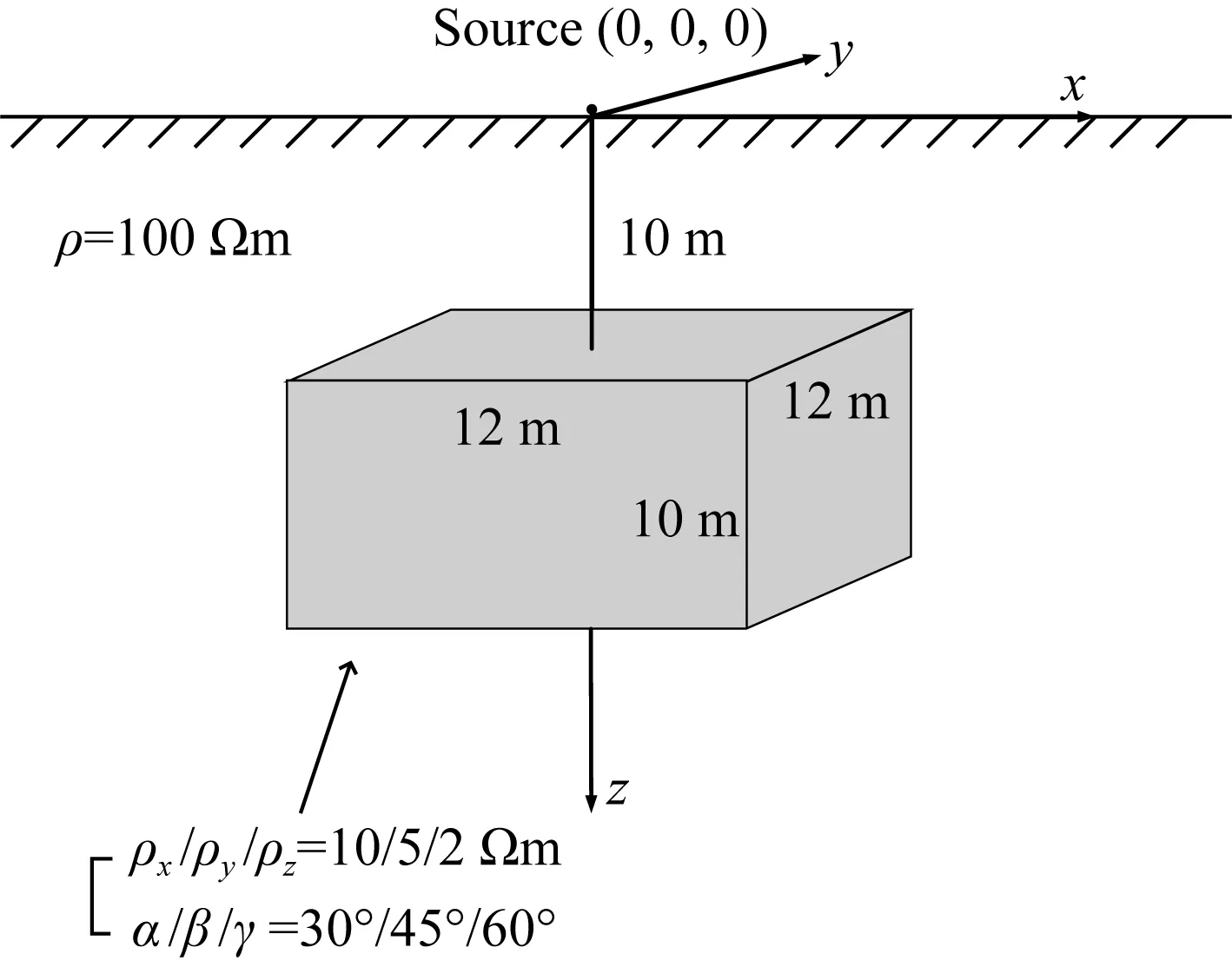
图2 模型1示意图Fig.2 Schematic diagram of model 1

2.2 迭代算法收敛性验证

为了分析异常体大小，异常体埋深以及异常体电阻率与算法收敛性的关系，利用图2模型进行验证，计算区域仍然为200 m×200 m×81 m.验证异常体大小与算法收敛性关系时，只改变异常体的大小，其他参数与图2模型的一致，对比结果如表1所示.验证异常体埋深与算法收敛性的关系时，只改变异常体的埋深，其他参数与图2模型的一致，对比结果如表2所示.

表1 异常体大小与算法迭代次数的关系Table 1 Relationship between the iteration times of algorithm and the size of abnormal body

表2 异常体埋深与算法迭代次数的关系Table 2 Relationship between the iteration times of algorithm and the depth of abnormal body

从表1和表2可看出，在满足精度要求的情况下，改变异常体的大小或者埋深，算法收敛时迭代次数不变，即异常体大小或埋深不影响算法的收敛性.

图3 本文算法和自适应有限单元法沿x轴方向测量得到的视电阻率图(a)以及相对误差图(b)(Expanding 0 m表示不扩边)Fig.3 Apparent resistivity (a) along the x-axis measured by the proposed algorithm and the adaptive finite element method and their relative errors (b) (‘Expanding 0m’ means calculation without expanding edge).

验证异常体电阻率值与算法收敛性的关系时，由于异常体为各向异性，无法像各向同性条件下直接给出异常体电阻率为常数，即各向异性异常体的电阻率为张量，为了便于分析，令异常体三个方向的欧拉角等于0，只改变异常体沿着x轴方向的电阻率主分量的值，保持另外两个方向的电阻率主分量不变，背景电阻率为100 Ωm，其他参数与图2模型的一致，结果如表3所示.从中可看出，异常电阻率与背景电阻率的差异决定了算法的收敛速度，异常电阻率与背景电阻率之间对比度越大，收敛速度越慢.另外，从表3可看出高阻异常比低阻异常的收敛速度更快.改变y轴方向电阻率主分量或z轴方向电阻率主分量也得到类似的结论，故不再赘述.

表3 异常体电阻率差异与算法迭代次数的关系Table 3 Relationship between the iteration times of algorithm and difference of abnormal body resistivity

2.3 算法效率分析

目前基于各向异性介质的直流电阻率法三维数值模拟算法的文献中，关于算法计算效率的阐述较少.为了研究本文算法在不同剖分网格下计算时间的变化规律，设计均匀半空间中存在两个异常体的模型来计算和验证.模型2如图4所示，计算区域为100 m×100 m×61 m，均匀半空间的电导率ρ0=100 Ωm，两个异常体大小为12 m×12 m×10 m，顶面至地面距离均为10 m，两个异常体之间距离为20 m，其中异常体A的电阻率为各向异性，电阻率主分量和欧拉角分别为ρ1/ρ2/ρ3=10/1000/1 Ωm，α/β/γ=0°/0°/0°，异常体B的电阻率为各向同性，ρB=10 Ωm.为了分析算法在不同剖分节点总数下的计算效率，令节点总数分别为101×101×81，201×201×81，301×301×81，401×401×81，501×501×81进行计算，不同节点总数下计算时间和占用内存如图5所示.从图中可看出随着剖分节点总数的增加，计算所需内存和时间呈近线性增长，其中节点总数为101×101×81(即826281)时计算所需内存为0.44 GB，计算时间仅为9.36 s，说明本文算法有较高的计算效率；节点总数为501×501×81(即20331081，节点数超过107)时计算所需内存为10.37 GB，计算时间为250.20 s，说明本文算法在微型计算机下即可计算剖分节点总数超过千万级的各向异性介质模型，并能较快地算出结果.

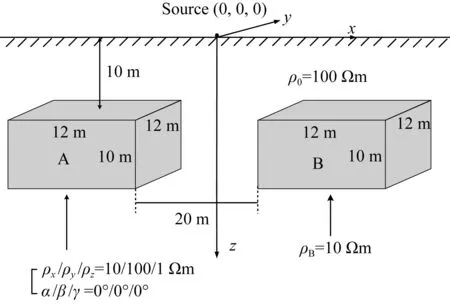
图4 模型2示意图Fig.4 Schematic diagram of model 2

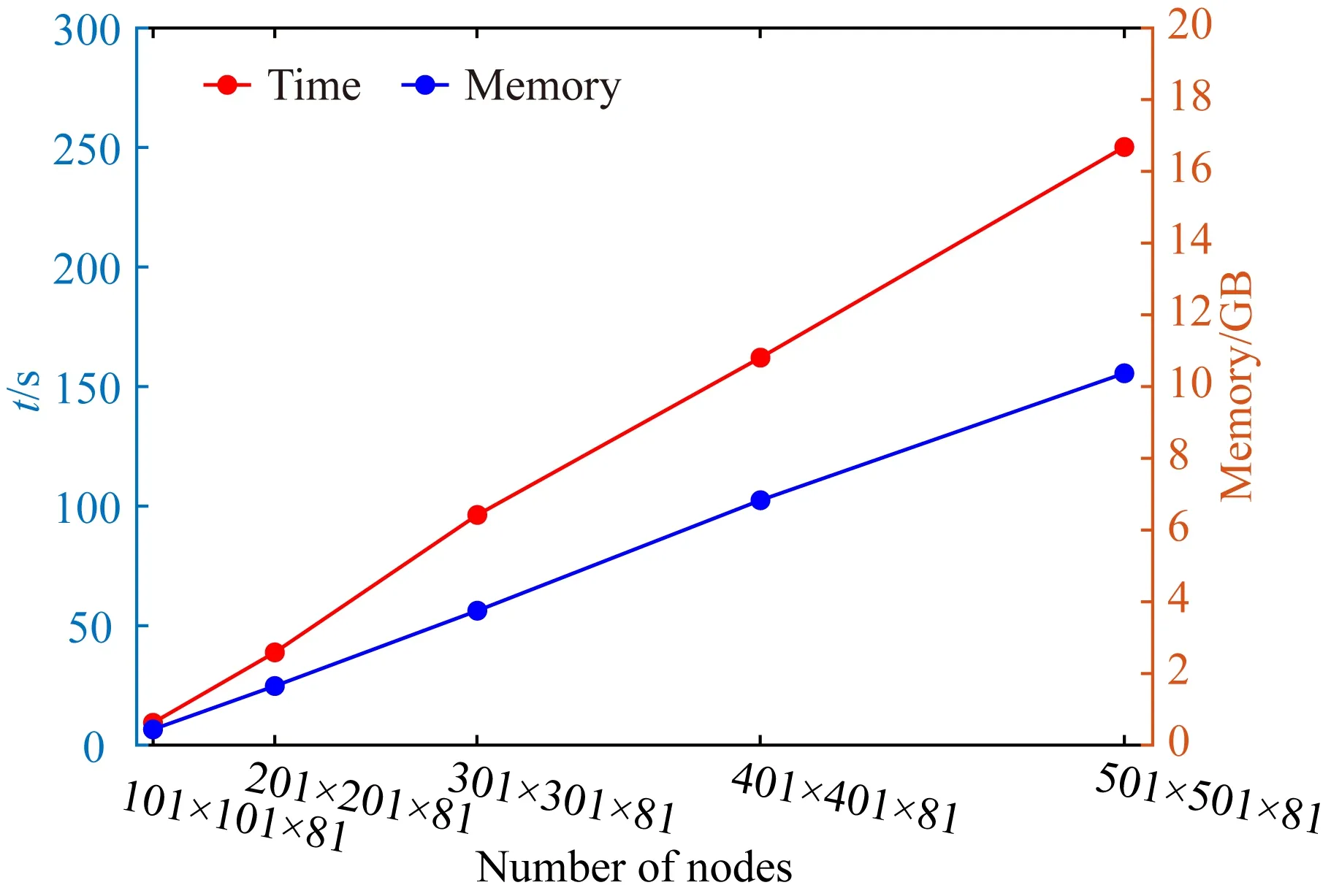
图5 本文算法在不同剖分节点下占用内存和计算时间Fig.5 The memory and time of the algorithm in different nodes

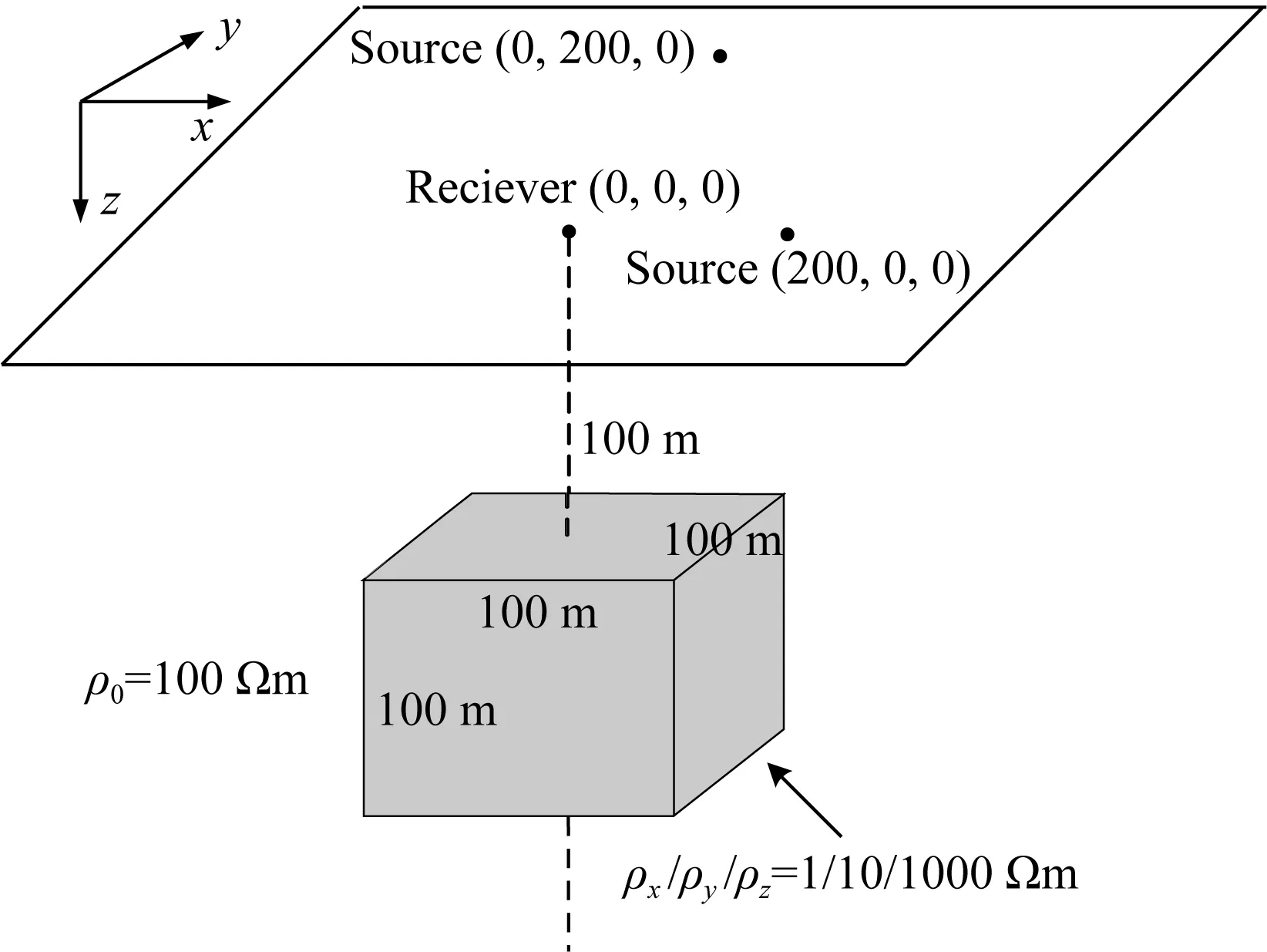
图6 模型3示意图Fig.6 Schematic diagram of model 3

2.4 模拟各向异性介质下的响应特征

通常，在野外为了观测到地下结构的各向异性特性，选择在不同的位置发射场源，并在同一个位置观测.为了模拟野外观测系统，采用半空间存在一电阻率各向异性棱柱体模型进行计算和分析，模型3如图6所示，背景为均匀各向同性半空间，电阻率ρ0=100 Ωm.异常体大小为100 m×100 m×100 m，异常体中心点在地面上的投影为坐标原点，异常体顶面至地面距离为100 m，异常体电阻率主分量和欧拉角分别为ρ1/ρ2/ρ3=1/10/1000 Ωm，α/β/γ=30°/45°/60°.采用二极装置测量，分别在点(200,0,0)和点(0,200,0)位置供电，供电电流大小为10 A，在原点(0,0,0)测量.通过测量可知，供电电极在(200,0,0)处时，原点(0,0,0)观测到的视电阻率值为98.11 Ωm；供电电极在(0,200,0)处时，原点(0,0,0)观测到的视电阻率值为95.10 Ωm.由此说明了该观测系统能反应出地下结构为各向异性的特性.

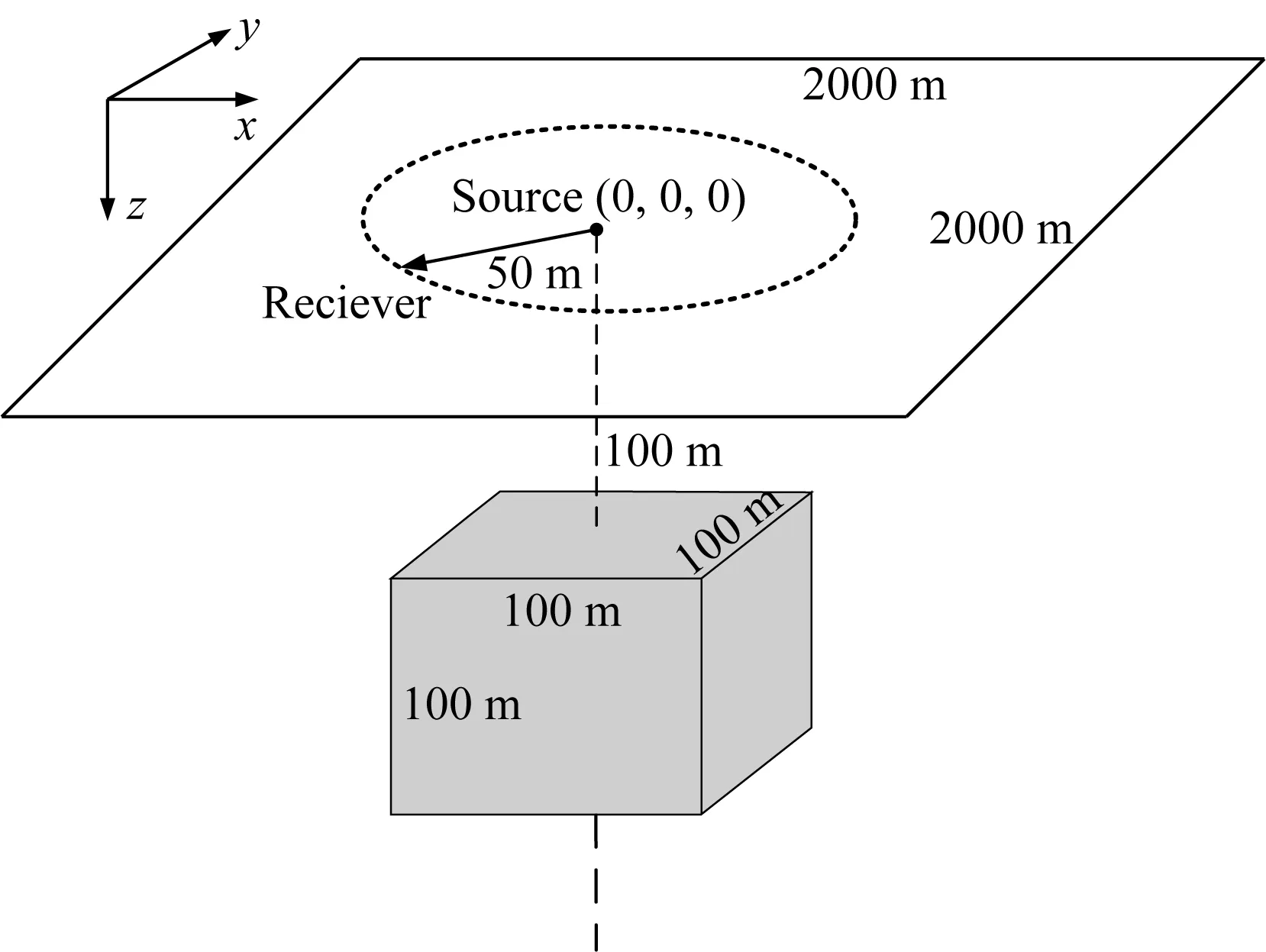
图7 模型6示意图图中带箭头实线表示收发距R=50 m，分别在相同收发距测量视电阻率.Fig.7 Schematic diagram of model 6The solid line with arrow indicates the receiving and transmitting distance R=50 m, the apparent resistivity is measured at the same receiving and transmitting distance around the source point.

为了进一步模拟和分析地下介质各向异性特性，仍然以各向同性半空间中存在一各向异性棱柱体模型(如图7所示)进行计算.计算区域为2000 m×2000 m×400 m，背景电阻率为ρ0=100 Ωm，异常体大小为100 m×100 m×100 m，异常体顶面至地面距离为100 m，异常体中心在地面上的投影为坐标原点，在该处放置供电电极，向地下供电电流大小为10 A，保持供电电极的位置不变，在距离供电电极为50 m的环形圆位置测量.下面对异常体电阻率取不同值的情况进行计算和分析：

(1)异常体为单轴各向异性时，令它的电阻率主分量分别为ρ1/ρ2/ρ3=1000/10/10 Ωm，ρ1/ρ2/ρ3=10/1000/10 Ωm，ρ1/ρ2/ρ3=10/10/1000 Ωm，三种情况进行计算，此时这三种情况下欧拉角均等于零.

(2)异常体为三轴各向异性时，令它的电阻率主分量为ρ1/ρ2/ρ3=10/1000/1 Ωm，其旋转的欧拉角分别为(a)α=0°/45°/90°/135°,β/γ=0°/0°; (b)β=0°/45°/90°/135°,α/γ=0°/0°; (c)γ=0°/30°/60°/90°,α/β=0°/0°，对这三种情况进行计算.

图8—9表示环形测量收发距R=50 m得到的视电阻率极向图.极化图中各点到中心点(供电电极)的径向长度表示视电阻率的大小，矢径方向表示测点的方位.为了更直观看出旋转不同欧拉角后得到的视电阻率值之间的差异，中心点根据实际情况取不同的起始值.

图8 异常体为各向同性或为单轴各向异性时，在收发距R=50 m环形测量得到的视电阻率极化图其中ρ1/ρ2/ρ3=10/10/10 Ωm表示异常体电导率为各向同性.Fig.8 Apparent resistivity is obtained by ring measurement at R=50 m in the case of isotropic anomalous or uniaxial anisotropic anomalous body. ρ1/ρ2/ρ3=10/10/10 Ωm means that the conductivity of the abnormal body is isotropic.

图8表示情况(1)下异常体为单轴各向异性，改变不同方向上电阻率主分量得到的极化图，从图中可看出，异常体为各向同性和各向异性时的视电阻率值不同，所以在实际应用中不可忽略地下介质的各向异性特性.另外，不同方位的电阻率单轴各向异性在同一测点计算得到的视电阻率值也不同.特别地，在此情况下z轴方向各向异性在地面上测量得到的视电阻率值大于沿着x轴或y轴方向各向异性测量得到的视电阻率值.

图9表示情况(2)下异常体为三轴各向异性时，异常体分别沿x轴，y轴及z轴方向旋转不同欧拉角得到的视电阻率极向图，其中环形测量收发距R=50 m.其中图9a表示沿x轴方向欧拉角α分别取0°/45°/90°/135°，而其他两个欧拉角为0°得到的视电阻率极化图；图9b表示沿y轴方向欧拉角β分别取0°/45°/90°/135°，而其他两个欧拉角为0°得到的视电阻率极化图；图9c表示沿z轴方向欧拉角γ分别取0°/45°/90°/135°，而其他两个欧拉角为0°得到的视电阻率极化图.从图9可看出，异常体沿着同一个方向旋转不同的欧拉角，得到的视电阻率不同，沿x方向欧拉角分别为45°和135°得到的视电阻率曲线关于x轴对称；沿着y方向欧拉角分别为45°和135°得到的视电阻率曲线关于y轴对称；而沿z方向欧拉角分别为0°和90°得到的视电阻率曲线关于45°和135°的轴线对称；沿x轴旋转得到的视电阻率值大于沿着y轴和z轴旋转得到的视电阻率数值；另外，无论异常体沿着哪个轴方向旋转，相同收发距的环形上测量得到的视电阻率曲线均为椭圆形.

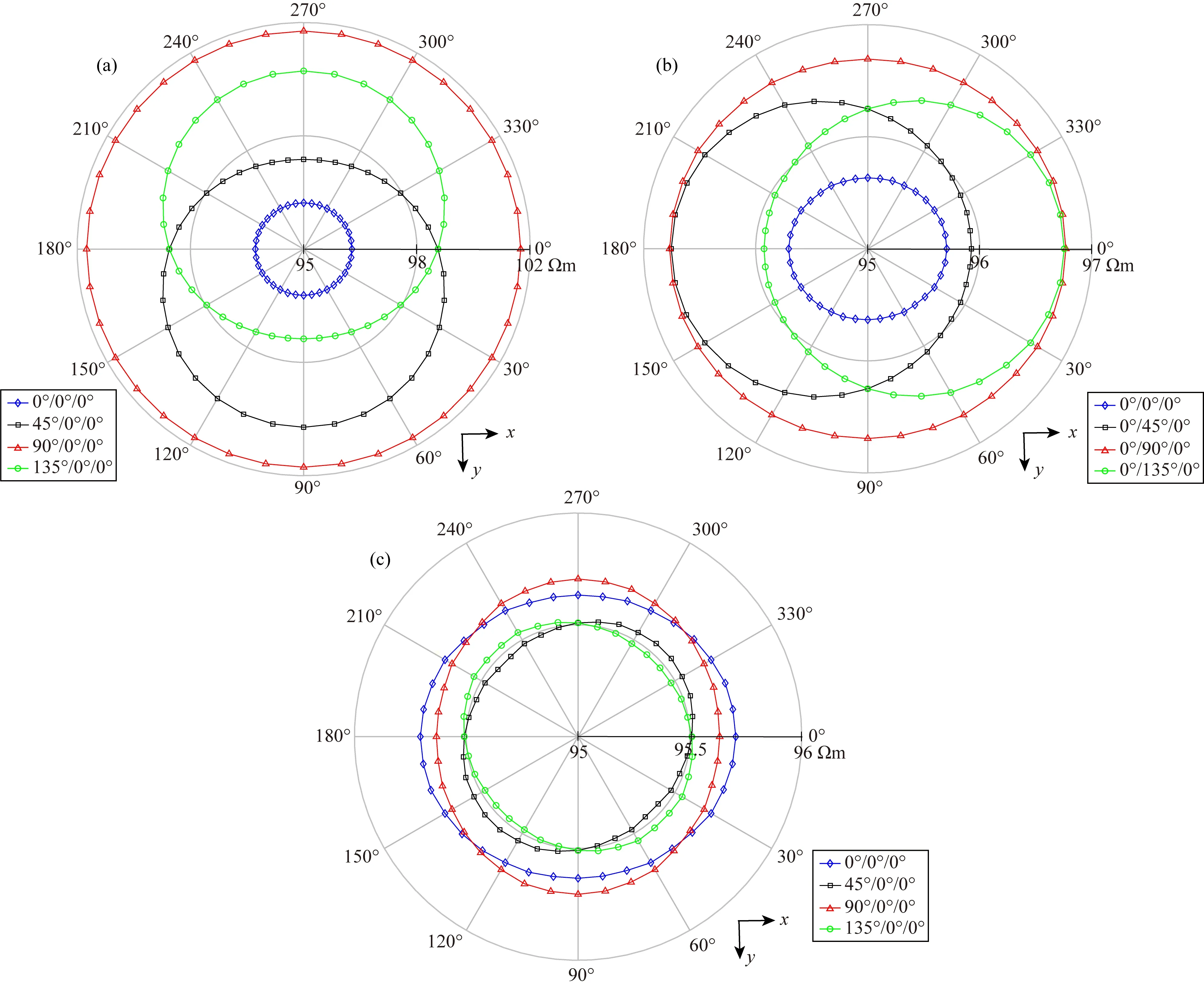
图9 异常体为三轴各向异性时，在收发距R=50 m环形测量得到的视电阻率极化图(a) α=0°/45°/90°/135°, β=0°, γ=0°; (b) α=0°,β=0°/45°/90°/135°,γ=0°; (c) α=0°, β=0°,γ=0°/45°/90°/135°.Fig.9 Apparent resistivity is obtained by ring measurement at R=50 m when the resistivity of the anomalous body is triaxial anisotropic

3 结论

本文将各向异性介质分成各向同性背景介质和各向异性异常介质，并提出了一种适用于计算各向异性介质的空间波数混合域直流电法三维数值模拟方法.该方法的策略是沿水平方向进行二维傅里叶变换，将空间域异常电位满足的三维偏微分方程转化成不同波数满足的一维常微分方程，这样将一个大规模三维数值模拟问题分解为多个一维数值模拟问题，具有高度并行性.该方法充分利用不同波数问题之间高度并行性，采用一维有限单元法求解不同波数满足的常微分方程，并引入压缩算子进行迭代，实现了直流电法三维数值模拟.

通过与自适应有限单元法对比验证精度，说明将各向异性介质分成各向同性背景介质和各向异性异常介质是可行的；分析半空间下存在两个异常体模型的计算效率，说明了本文算法在微型计算机下能较快算出剖分节点总数超过千万的模型的结果；异常体为各向异性情况下，按不同方向旋转欧拉角的响应特征结果表明，异常体为各向异性比异常体为各向同性的响应特征更复杂；各向异性异常体沿着不同的方向旋转得到的视电阻率不同，即使在同一方向上旋转不同角度，得到的视电阻率差异也很大.特别说明的是，本文算法具有高度并行性以及可用于带地形的复杂模型的计算，后续将研究它基于OpenMP或GPU平台的并行算法以及带地形的复杂模型的计算.

附录A

(A1)

(A2)

(A3)

(A4)

(A5)

xxe、yye、zze对应为单元内三个方向的电流密度.由于z=zmax表示最后一个节点，因此，式(22)中的最后一项可以扩展为

(A6)

式中，

(A7)