正切平方量子阱中的非线性光学折射率

赵 庄， 李学超， 张粮成， 段一名

(安徽理工大学 力学与光电物理学院，安徽 淮南 232001)

在过去的几年中，与半导体材料中子带间跃迁相关的非线性光学特性引起了理论和应用物理方面研究人员的广泛关注.由于半导体生长技术的进步，可以产生不同类型的低维半导体结构，如量子点、量子阱、量子线和超晶格[1-7].正是由于低维半导体结构的约束增强，在这些低维半导体结构中出现了许多新的非线性光学特性.这种特性已成为高速光电调制器、远红外光电探测器、半导体光放大器等许多光电器件的重要物理基础[8].另外，随着纳米制造技术的逐渐成熟，多种形状的量子阱的制备逐渐成为现实，如抛物形量子阱、方正量子阱等.这些不同形状的量子阱影响着电学、光学和输运特性.此外，电场或磁场的应用以及静水压力或温度等外部扰动，都改变了被限制在量子阱中的载流子的量子态.

近年来，许多研究人员对非线性光学性质进行了理论研究.You等[9]研究了静体压力和磁场对AlGaAs/GaAs抛物形量子阱非线性光学特性的影响；Hu等[10]研究了位置相关质量对量子阱中非线性光吸收系数和折射率变化的影响；Bouzaïene等[11]研究了静压力和温度对AlGaAs/GaAs量子点透镜形状的非线性光学整流的影响；Guanguly等[12]研究了存在和不存在高斯白噪声的2种情况，在静水压力和温度的共同影响下，杂质掺杂量子点的光学整流、二次谐波产生和三次谐波产生的特性；Karabulut等[13]研究了外加电场和磁场以及静水压力的综合效应下GaAs-Ga1-xAlxAs非对称双量子阱中的非线性光学整流和光学吸收；Dahiya等[14]研究了强激光场对δ掺杂GaAs量子阱中子带间光吸收和折射率变化的影响.然而在考虑到温度的作用下，具有Utan2(πy/d)势的正切平方量子阱的非线性光学性质尚未被研究，笔者从理论上研究在温度和流体静压作用下正切平方量子阱中的非线性光学折射率变化情况.

本文中，笔者首先通过求解薛定谔方程得到了本征函数和能量特征值，利用密度矩阵法和迭代法得到了RIC的解析表达式，然后给出了典型正切平方量子阱的数值计算和详细讨论，最后做了简要总结.

1 理论推导

1.1 能量特征值和特征函数

考虑一个电势为Utan2(πy/d)的电子限制在系统中.当有效质量近似以及在流体静压、温度作用的情况下，系统的哈密顿量可以写成如下形式[8]：

(1)

V(y)=Utan2(πy/d),

(2)

其中ћ代表普朗克常数，y代表量子阱的生长方向，d和U分别代表量子阱的直径和电势，根据(2)可知d和U对限制电位V(y)的影响很大.P表示流体静压，T表示温度，m(P,T)*表示量子阱中依赖于压力和温度的电子有效质量，由下式给出[9]：

(3)

其中m0表示自由电子质量，C=7.51 eV表示与动量矩阵元有关的能量，A=0.341 eV表示自旋轨道分裂能量.α(P,T)表示半导体在中心点的能隙随温度和静水压力的变化，由下式给出：

α(P,T)=α(0,T)+0.012 6P-3.77×10-5P2,

(4)

当考虑了流体静压和温度的影响时，y方向的薛定谔方程有以下形式[11]：

(5)

通过求解这个方程，可以得到能谱

(6)

同时可以推导出波函数

(7)

当n=0,1,2,3,…时，gn(ξ)分别取

g0(ξ)=1，

g1(ξ)=ξ，

…

1.2 折射率变化

在得到能量及其相应的波函数后，用密度矩阵法和迭代程序可以计算出非线性光学折射率变化，可以假设系统受到一个电磁场的激励，该电磁场表示为

密度矩阵算符ρ的演化遵循以下随时间变化的Liouville方程[13]：

(8)

其中ρ(0)为未扰动的密度矩阵算符，H0为未受电磁场影响的系统哈密顿量，Γij为弛豫率.

(8)可以通过以下迭代方法计算[14-15]：

(9)

(10)

该系统的电极化可扩展为[16]

(11)

(12)

其中V表示互相作用的体积，Tr表示矩阵的迹(主对角元素之和).采用相同的紧密度矩阵方法和迭代方法，可以得出如下线性和三阶非线性磁化率[17]：

(13)

(14)

利用紧密度矩阵方法和迭代方法,系统的线性和三阶非线性折射率变化可以写为[18-19]

(15)

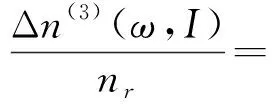
(E10-ћω×[E10(E10-ћω)-(ћΓ0)2])}}.

(16)

折射率的总变化可以表示为

(17)

2 结果与讨论

对正切平方量子阱的折射率变化的分析中，主要探讨流体静压P、温度T、QWs的直径d以及电势U对折射率变化的影响.所采用的参数为m*=0.067m0(m0表示自由电子质量)，σv=5.0×1024m-3，μ=4π×107Hm-1,ε0=8.85×10-12fm-1.

如图1所示，首先讨论了流体静压对正切平方量子阱非线性光学折射率变化的影响.取U=45 meV，T=200 K，d=25 nm，做出了不同流体静压下光学折射率随入射光子能量ћω的变化关系曲线图，流体静压分别取P=40,50,60 kbar.可以看出，随着P的增加，RCI共振峰向低能方向移动，即发生“红移”.造成这种行为的物理原因是静水压力增加了电子的有效质量(见(3))，继而反过来又导致了强度约束的降低.不仅如此，通过观察图1还可以发现，RIC共振峰的值并没有随着流体静压的增大而发生明显变化，这是因为流体静压在小范围内的变化对光学折射率变化造成的影响是微弱的.

图1 当U=45 meV，T=200 K，d=25 nm，P=40，50，60 kbar时， 光折射率随入射光子能量ћω的变化关系曲线Fig.1 The RIC as a Function of the Photon Energy ћω for P=40，50，60 kbar，with U=45 meV，T=200 K，d=25 nm

如图3所示，讨论了温度对正切平方量子阱非线性光学折射率变化的影响.取U=45 meV，P=50 kbar，d=25 nm，做出了温度不同时光学折射率随入射光子能量ћω的变化关系曲线图，T=100，200，300 K.可以看出，随着温度的升高，RIC共振峰向高能方向移动，即发生“蓝移”.这种现象产生的原因是升高温度会导致电子有效质量降低(见(3)).另外，为了达到限制电子的目的，子带能级之间的跃迁需要更大的能量，进而增大了共振峰对应的入射光能量.

图2 当U=45 meV，T=200 K，P=50 kbar，d=20，25， 30 nm时，光折射率随入射光子能量 ћω的 变化关系曲线Fig.2 The RIC as a Function of the Photon Energy ћω for d=20，25，30 nm，with U=45 meV，T=200 K， P=50 kbar

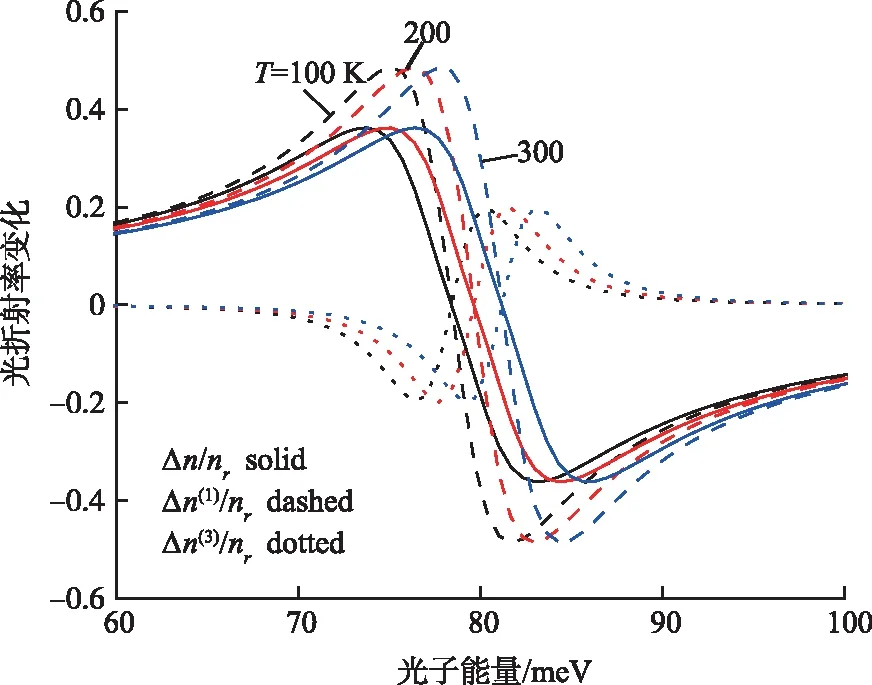
图3 当U=45 meV，P=50 kbar，d=25 nm，T=100， 200，300 K时，光折射率随入射光子能量ћω 的变化关系曲线Fig.3 The RIC as a Function of the Photon Energy ћω for T=100，200，300 K，with U=45 meV，P=50 kbar， d=25 nm

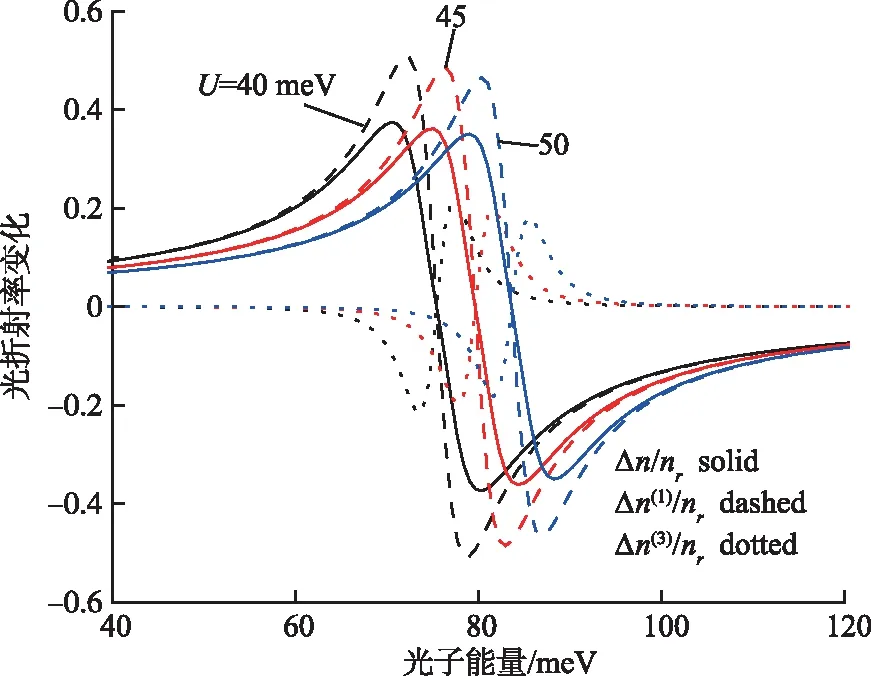
图4 当T=200 K，P=50 kbar，d=25 nm，U=40，50，60 meV时，光折射率随入射光子能量ћω的变化关系曲线Fig.4 The RIC as a Function of the Photon Energy ћω for U=40，50，60 meV，with T=200 K，P=50 kbar，d=25 nm

3 结 论

通过求解薛定谔方程，得到了本征函数和能级，然后使用密度矩阵理论和迭代方法推导出正切平方量子阱的光学折射率的解析表达式，进而从理论上研究了部分因素对正切平方量子阱中非线性光学折射率的变化.通过数值计算发现，流体静压以及QWs直径的增加会导致“红移”，这是由于P和d的增加使得电子在系统中的约束变弱，此时RIC共振峰向低能方向移动.随着温度的升高电子的有效质量降低，导致了RIC峰向高能方向移动，即“蓝移”.另外，随着电势U的增加量子受限效应增强，导致RIC共振峰向高能方向移动.最后，该研究结果能为非线性光学领域的改进和新型电子光学器件的开发提供理论价值.