2个二能级原子与最小热环境作用系统中的量子特性

朱冬梅, 萨楚尔夫， 苏少龙

(内蒙古师范大学 物理与电子信息学院，内蒙古 呼和浩特 010022)

2个耦合原子与光场相互作用系统中呈现出的量子现象是量子光学研究领域中引人注目的研究课题之一.而这一相互作用系统中的量子纠缠作为一种重要的物理资源，可在量子信息科学中发挥十分显著的作用.在实际情况中，由于真实的量子系统不可避免地会与环境耦合而产生相互作用，这种耦合作用会破坏系统内各子系统间的量子纠缠或相干性，使系统本身所具有的量子特性受到影响，如会导致退相干现象的发生[1]等.近年来，与环境相互作用的量子耦合系统的动力学问题[2-7]是研究人员感兴趣的课题之一.对于一个复合量子系统，可以通过考虑子系统之间的相互作用得到表征系统演化的动力学主方程.研究发现，在不同环境条件下主方程演化形式存在着一定的差异[8].在不同相互作用条件下，因系统的主方程演化形式不同，从而导致不同的结果.研究结果[9-10]还表明，环境因素对量子系统的演化起重要作用，这意味着需要对环境因素进行更精细的划分，才能使所得耦合系统的主方程更准确地表征演化过程.因此，就有关问题分类从而进行细致的研究是十分必要的.

目前人们对量子系统可实施的调控手段和途径越来越多，其中具有较少自由度的微小环境对所研究系统量子特性演化的影响，吸引了不少研究者的兴趣.这些系统受到关注的原因主要包括：这类耦合量子系统的某些物理特征量可解析表示，便于分析过程和讨论结果；微小环境与所研究系统的耦合也可产生明显的扰动[11-13]，使系统的演化产生较明显的变化，故利用此简单模型可深入了解环境因素对系统演化的影响.具体而言，考虑一个与热环境耦合的2原子相互作用系统[4]的模型，假设其中原子1是孤立的，原子2与单模热辐射场相互作用，这里热辐射场可以起到微小环境的作用.利用这一相互作用模型，可研究在不同温度、不同耦合强度下，系统中2原子间的量子纠缠和相干演化特性.在以往的研究中，主要考虑了初始时刻上述系统中2原子处于非纠缠分离态的情况；而系统中2原子处于纠缠态时，辐射场处于不同温度、原子与辐射场相互作用强度、原子与原子相互作用强度对系统中原子间纠缠和相干演化的影响还未见报道.

本文中，笔者研究了上述系统中2原子处于纠缠态，在给定参数条件下，系统中2原子间的纠缠、相干特性和线性熵随时间的演化特性.

1 理论模型及推导

讨论由2个二能级原子和1个量子化热辐射场所组成的系统，其中一个原子不与辐射场耦合，而另一个原子与单模辐射场耦合.假设原子的跃迁频率与原子和场之间相互作用的共振频率相等(ω1=ω2=ω)，则系统的哈密顿量可写为(ћ=1)

(1)

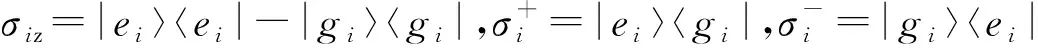
ρI(t)=e-iH1tρ(0)eiH1t,

(2)

ρ(0)=ρq1,q2(0)⊗ρf(0),

(3)

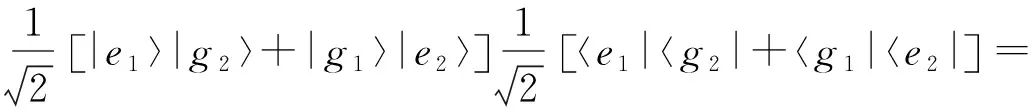
(4)

(5)

频率为ω单模热场态的光子数分布如下(T为有效温度)：

(6)

在相互作用绘景中，系统的态矢演化服从薛定谔方程

(7)

此系统的态矢为

|ψI(t)〉=C1,n(t)|e1,e2,n-1〉+C2,n(t)|e1,g2,n〉+

C3,n(t)|g1,e2,n〉+C4,n(t)|g1,g2,n+1〉.

(8)

将上述关系式代入薛定谔方程，得到系数Cj,n的耦合微分方程组

(9)

因此系统的解可以表示为

(10)

矩阵元中的n表示光子数，n=1,2,3,….

求解方程组(9)，(10)，经过较冗长的计算可得以上公式中的系数表达式

(11)

其中

(12)

若初始条件满足

(13)

此时几率振幅Cj,n(t)可表示为

(14)

因此系统的时间演化密度算符为

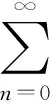
(15)

通过对场取迹ρq1,q2(t)=Trf[ρI(t)],可将2个二能级原子系统的约化密度算符表示为

(16)

这种类型的态被称为X态[14].

2 微小环境对系统中双原子间纠缠的影响

原子与原子间的相互作用导致2原子间的量子纠缠效应.为度量2子系统之间的纠缠，Wootters引入了共生纠缠度C[15]来表征2个子系统之间的量子纠缠.C定义为

(17)

其中ξi是厄米矩阵M(t)的本征值，σy是泡利矩阵

(18)

共生纠缠度的取值范围为0～1，共生纠缠度值越大，纠缠越强.对于非纠缠态，C=0；而C=1则意味着系统处于最大纠缠态.

由以上可知,此2原子的密度算符ρq1,q2(t)可表示为

(19)

(20)

对于X态的特殊情况，可将Λ(t)表示为

(21)

下面通过数值模拟的方法，利用初始条件以及关系式(17)～(21)，讨论在给定耦合强度和温度下，2原子间的共生纠缠度随时间的变化情况.

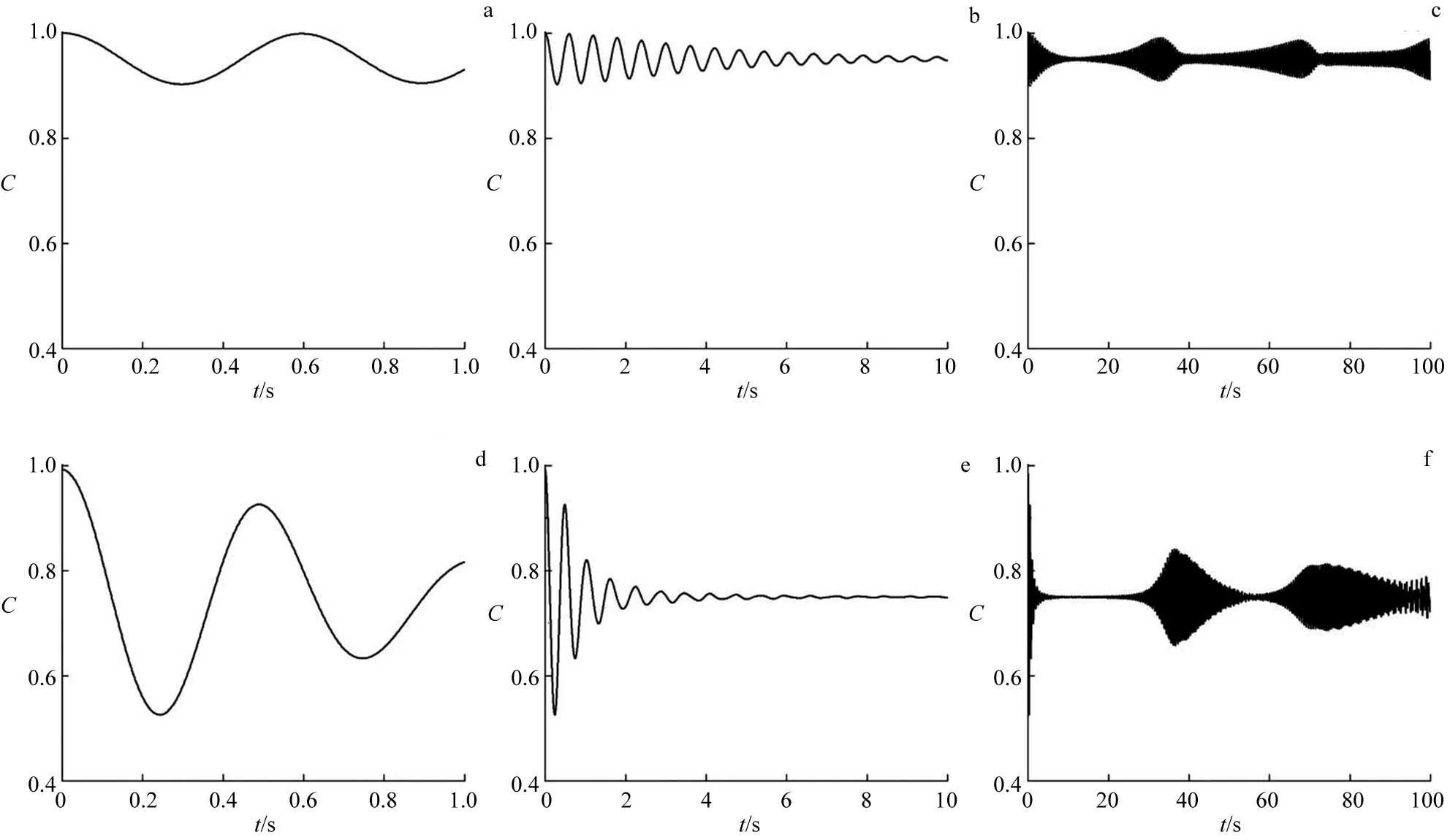
图1 g=0.1λ，不同时间尺度下,2原子系统共生纠缠度随时间的变化曲线Fig.1 Concurrence of the Two-qubit System as a Function of Time for g=0.1λ and for Different Time-scales

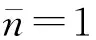
图2 g=0.5λ,不同时间尺度下,2原子系统共生纠缠度随时间的变化曲线Fig.2 Concurrence of the Two-qubit System as a Function of Time for g=0.5λ and for Different Time-scales

3 双原子系统的量子相干性及线性熵

3.1 量子相干性

量子相干性是量子理论中的基本概念，也是一种可以利用的资源[19].系统相干性可利用复合系统中2个原子间的约化密度矩阵的非对角元来表示，相干性的量化形式可通过定义的Cl1给出表达式

(22)

利用(22)分析有关参量对Cl1随时间演化的影响.由图3和图4可见，演化曲线从不规则逐渐趋于稳定，但并没有出现相干为0的现象.对于弱耦合情形(g=0.1λ)，图3a～c所示的相干演化曲线与量子纠缠演化曲线非常相似.随时间的延长振幅短期内连续下降，但在后期出现了塌缩复原再塌缩再复原的准周期行为；增大平均光子数，Cl1演化曲线整体下移，表明量子相干性减小，观察可知函数值的取值范围变大，即振荡幅度变大.由图3e可见，Cl1取值逐渐趋于0.9，在长时间尺度图3f中可以观察到，演化曲线出现塌缩—复原现象，与图3c相比，平均光子数越大，塌缩—复原的间隔时域越长.

图3 g=0.1λ，不同时间尺度下，2原子系统量子相干随时间的变化曲线Fig.3 Quantum Coherence of the Two-qubit System as a Function of Time for g=0.1λ and for Different Time-scales

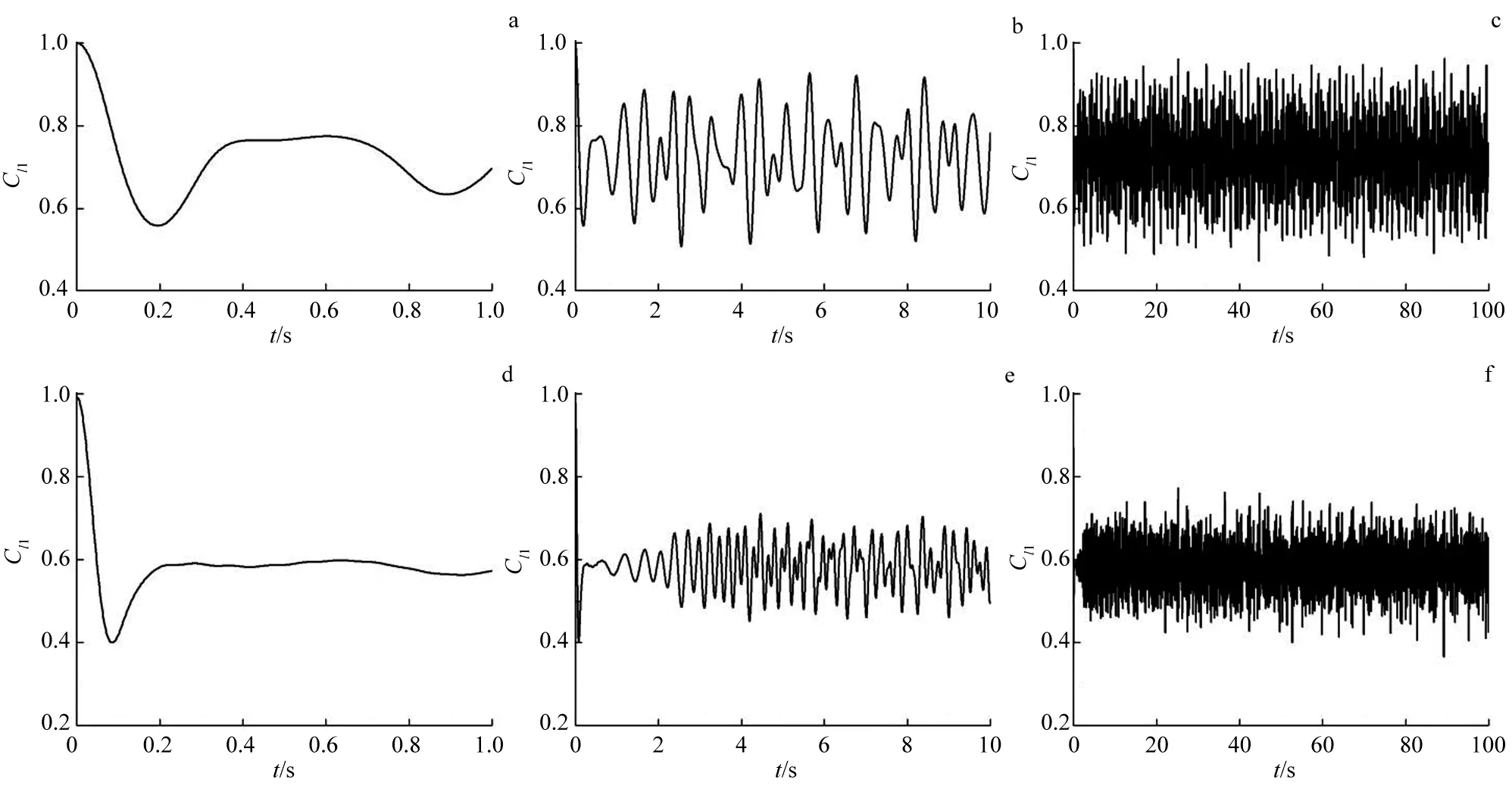
图4 g=0.5λ,不同时间尺度下，2原子系统量子相干随时间的变化曲线Fig.4 Quantum Coherence of the Two-qubit System as a Function of Time for g=0.5λ and for Different Time-scales

由图4可见，在较强耦合情况下(g=0.5λ)，相干退化现象更明显.与图2相比，在初始时刻，Cl1=1，相干性最强，整个演化过程中未出现完全退相干现象.由图4d～f可见，增大平均光子数相干演化曲线下移，表明平均光子数增大使2原子相干性减小，而且无论在强或弱耦合条件下，在长时域上(图3e、图4e)可观察到相干特性随时间的剧烈无规则振荡行为.

3.2 第1个原子的线性熵

为研究第1个原子的动力学演化过程，需求出其约化密度算符.通过对第2个原子q2和辐射场f取迹，可得第1个原子的约化密度算符ρq1(t)=Trq2,f[ρI(t)]，则有

ρq1(t)=ρee(t)|e1〉〈e1|+ρgg(t)|g1〉〈g1|+ρeg(t)|e1〉〈g1|+ρge(t)|g1〉〈e1|.

(23)

为了描述第1个原子状态的纯度，可引入线性熵[20]的概念.线性熵可定义为

(24)

(25)

线性熵可表示2个子系统之间关联的程度，子系统之间的关联越紧密纠缠也越强.粒子数反演是与几率振幅相关的物理量,也是原子与光场相互作用体系的重要特性之一，可以表示为上下两能级间的概率之差

W(t)=ρee(t)-ρgg(t)=1-2ρgg(t).

(26)

结合以上公式，线性熵还可表示为

(27)

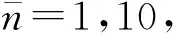
图5 g=0.1λ，不同时间尺度下，2原子系统线性熵随时间的变化曲线Fig.5 State Purity of the Qubit 1 as a Function of Time for g=0.1λ and for Different Time-scales

由图5可知，在弱耦合下(g=0.1λ)，第1个原子的线性熵为0.499 5～0.500 0，振幅的变化幅度不大，在初始时刻，线性熵取最大值0.5.增大平均光子数，如图5d～f所示，其时间演化曲线与图5a～c相似，但振幅变化范围缩小，振幅平均值略变大.与图5相比，在强耦合下(g=0.5λ)，图6呈现出与之不同的变化形式，其演化过程中取值更显不规则.由图6a可知，在t≈0.25 s时，S(t)取极小值，随时间的延长，振幅变化无规则，在长时域图6c中可以看到，线性熵在0.455～0.500时形成剧烈无规则振荡.当平均光子数较大时，即图6d～f，短时间尺度内，在初始阶段线性熵取最大值0.5，其振幅变化较小.对比图6c与图6f可知，平均光子数变大，线性熵的取值范围上移.同时图5和图6反映出演化的共同特点，即随着时间的延长，小微外环境对耦合系统的影响逐渐发挥作用，从而观察到耦合系统中有关的量子特性随环境参量的变化，小微外环境导致演化过程发生显著改变.

图6 g=0.5λ，不同时间尺度下，2原子系统线性熵随时间的变化曲线Fig.6 State Purity of the Qubit 1 as a Function of Time for g=0.5λ and for Different Time-scales

4 结 论

研究了2个二能级原子系统与小微环境相互作用的简单模型，其中一个原子孤立，另一个原子与单模热场耦合，系统中2原子初态处于最大纠缠态，分别讨论了弱、强耦合作用下，场的平均光子数取不同值对2原子间纠缠、相干特性及线性熵的影响.结果表明：在弱耦合作用下，共生纠缠度的整体取值较大，演化过程中出现了振荡的塌缩与复原再塌缩再复原的准周期行为.对于强耦合情况，原子间纠缠明显减弱，随着时间的延长，共生纠缠度表现出锯齿型的剧烈振荡行为.无论强、弱耦合作用，平均光子数增大时，共生纠缠度演化过程中2原子间纠缠减小.另外，在强耦合且平均光子数较大时，出现了在一定时域内纠缠消失的情况，即量子纠缠突然死亡又再生的现象.观察热环境对系统相干性演化过程的影响可发现，系统相干特性的时间演化过程与纠缠的演化过程相似，不同之处在于没有出现相干消失的现象，在弱耦合作用下相干性也出现了塌缩—复原的准周期行为，在较长尺度上呈现为不规则振荡形式，对于强耦合情形，演化过程振荡更剧烈，塌缩—复原的变化特征消失，表征系统相干特性的物理量平均值减小，即相干性整体减小.线性熵可表征原子态的纯度，随着时间的延长，弱耦合作用下随光子数的变化，线性熵取值范围略有变化，但在强耦合作用下，线性熵取值范围随平均光子数的增加而出现上移.总之，系统耦合强度以及代表热环境参数的平均光子数，对2个二能级原子系统的共生纠缠度、量子相干和原子的信息熵演化都会产生显著的影响.