Furstenberg族的一些性质研究

周小凯，张思汇

(上海理工大学 理学院，上海 200093)

设(X,f)是一个拓扑动力系统(简称动力系统或系统),其中X是紧致度量空间(度量为d),f:X→X是连续映射。对n∈+,称fn=f…f为f的n次迭代。对n=0,约定f0=id,其中id为恒同映射[1]。

对于动力系统(X,f),如果U,V⊂X,定义回复时间集为

(1)

我们称系统(X,f)或f是传递的,如果对X的任意两个非空开子集U,V,回复时间集Nf(U,V)非空;称系统(X,f)是弱混合的,如果乘积系统(X×X,f×f)是传递的;称系统(X,f)是强混合的,如果对X的任意两个非空开子集U,V,存在N∈+,使得{N,N+1,…}⊂Nf(U,V)。Furstenberg[2]证明了对每个正整数n,系统(X,f)是弱混合的，意味着n次乘积系统(Xn,f(n))是传递的。即: 设(X,f)是一个拓扑动力系统,若(X×X,f×f)是传递的当且仅当对每个n∈+,乘积系统(Xn,fn)(n次)也是传递的,其中Xn=X×…×X(n次),fn=f…f(n次)。

对于一个动力系统(X,f),我们称点对(x,y)∈X为distal的,是指存在ε>0,

(2)

另外,如果存在ε>0,使得对任意点对(x,y)且x≠y,则称这个动力系统(X,f)是distal的。

动力系统(X,f)称为是等度连续的,是指对任意ε>0,存在δ>0,使得对任意满足x,y∈X且ρ(x,y)<δ时,对任意的n∈+,都有

ρ(fn(x),fn(y))<ε。

(3)

在本文中,我们考虑在L1(I,I)={g:I→I}(其中g是勒贝格可积函数,I=[0,1])空间中的动力学行为。我们定义对所有的φ,φ∈L1(I,I),在L1(I,I)上的度量ρ为

(4)

其中μ为勒贝格测度。不难验证(L1(I,I),ρ)是完全可分的度量空间。

动力系统(I,f),其中I=[0,1],由Hf:L1(I,I)→L1(I,I),φfφ定义它的泛函包络(L1(I,I),Hf)。不难验证,若Hf是一致连续的,则(L1(I,I),Hf)也是一个动力系统。Auslander等[3]证明系统的泛函包络也具有系统的一些性质。Chen等[4-6]研究动力系统的泛函包络具有的一些性质。

Chen等[6]证明了如下命题:

命题A[6]如果(I,f)是distal的,则(L1(I,I),Hf)也是distal的。

命题B[6]如果(I,f)是等度连续的,则(L1(I,I),Hf)也是等度连续的。

1 前期准备

(5)

用族来描述动力学性质的研究至少可以追溯到Gottschalk等[7]的研究,并且由Furstenberg[8]作进一步推广。

定义1对于动力系统(X,f),F是Furstenberg族,点对(x,y)∈X称为是F-distal的,若存在ε>0,则

{n∈+:ρ(fn(x),fn(y))≥ε}∈F。

(6)

另外,如果存在ε>0,使得对任意点对(x,y)且x≠y,都有

{n∈+:ρ(fn(x),fn(y))≥ε}∈F，

(7)

则称这个动力系统(X,f)是F-distal的。

定义2对于动力系统(X,f),F是Furstenberg族,称系统(X,f)为F-等度连续的,是指对任意ε>0,存在δ>0,对任意x,y∈X且ρ(x,y)<δ,都有

{n∈+:ρ(fn(x),fn(y))<ε}∈F。

(8)

2 主要证明与结论

命题1如果(I,f)是F-distal的,则满足任意ρ(φ,φ)>0的点对φ,φ∈L1(I,I)在系统(L1(I,I),Hf)中是F-distal的。

证 假设(I,f)是F-distal的,则存在ε>0,使得

{n∈+:ρ(fn(x),fn(y))≥ε}∈F。

(9)

设φ,φ∈L1(I,I),且ρ(φ,φ)>0,取

A={x∈I:φ(x)=φ(x)} 和B={x∈I:φ(x)≠φ(x)},

则μ(B)>0。对任意n∈{n∈+:ρ(fn(x),fn(y))≥ε},我们有

(10)

因此

{n∈

(11)

于是动力系统(L1(I,I),Hf)是F-distal的。

命题2设(I,f)是F-等度连续的,则对任意的ε>0,存在δ>0,使对任意的φ,φ∈L1(I,I)且ρ(φ,φ)<δ,有(L1(I,I),Hf)是F-等度连续的。

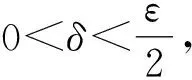
(12)

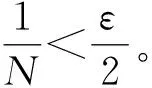
A={x∈I:|φ(x)-φ(x)|<δ} 和B={x∈I:|φ(x)-φ(x)|≥δ}。

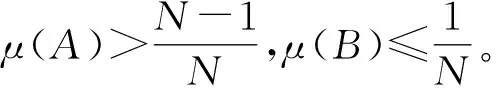
(13)

则

(14)

因此(L1(I,I),Hf)是F-等度连续的。