基于蚁群算法的深海着陆车路径规划

2022-07-05郭威吴凯周悦孙洪鸣徐高飞高森

兵工学报 2022年6期

郭威，吴凯，周悦，孙洪鸣，徐高飞，高森

(1.中国科学院深海科学与工程研究所，海南三亚 572000；2.中国科学院大学，北京 100049；3.上海海洋大学工程学院，上海 201306)

0 引言

海洋蕴藏着丰富的资源，是维持人类社会可持续发展的重要战略空间。自主式深海着陆车是一种能够在海底环境下完成大范围位置序列探测、定点位时间序列测量及精细化重载作业的可移动海底探测平台。深海着陆车受自身体积、质量等限制，其所携带电池电量有限，从而对着陆车能否在有限能源条件下实现长距离航行提出了挑战。因此，如何在复杂三维海底环境中规划出一条着陆车安全、能耗低、用时短的路径，具有重要的工程应用意义。

目前，水下机器人路径规划方法主要有遗传算法、粒子群优化算法、神经网络算法、蚁群算法等，而蚁群算法因具有反馈性好、鲁棒性强、分布式计算能力强等优点，在水下机器人路径规划领域得到广泛应用。刘贵杰等提出基于能耗最优改进蚁群算法，通过对自主式水下机器人(AUV)进行水动力分析得到能耗计算公式，以能耗作为启发因子和评价函数指标，一定程度上提高了AUV的续航能力。潘昕等提出基于遗传蚂蚁混合算法的AUV全局路径规划，以航路消耗、上浮或下潜风险等作为评价指标，提高了路径的经济性与安全性。张汝波等提出基于改进蚁群算法的AUV路径规划，通过运用蚁群间信息素调整方法避免了算法的停滞及信息素过于集中问题，提高了航路的搜索能力；张楠楠等研究AUV在三维环境中改进蚁群算法路径规划，以路径距离、通行性及姿态角作为启发函数来搜索最优路径，并将路径长度和光滑度作为评价指标，一定程度上减少作业时的能耗。

本文针对自主式深海着陆车长续航应用需求，以能耗低和路径短为优化目标，通过行驶阻力分析和驱动电机能耗测量与分析来建立着陆车运动能耗模型，进而开展基于蚁群寻优的能耗- 距离路径规划算法研究。

1 深海三维空间抽象建模与路径生成规则

三维海底空间复杂，建立合理的环境模型是开展深海着陆车路径规划的关键。

1.1 三维空间抽象建模

海底三维环境数据通过科考船测绘获得，将其用于三维空间抽象建模：首先以三维空间环境(见图1)左下角顶点作为原点建立坐标系，其中轴、轴、轴分别对应纬度、经度、垂直于海平面的方向，且′、、分别为深海着陆车作业规划空间3个方向的最大尺度，深海着陆车起点和终点分别位于平面和′′′′上，三维环境路径规划空间如图1(a)所示；然后对三维路径规划空间采用栅格等分法划分出路径规划所需的网格点，即沿着′将规划的空间-′′′′进行等分，得到+1个平面，再对+1个平面沿着、分别进行和等分，获得三维空间划分点集，该集合中每一个点对应着序号坐标(,,)和位置坐标(,,)，其中、、分别为沿′、、的划分序号，∈0,1,…,-1,；∈0,1,…,-1,；∈0,1,…,-1,，平面划分如图1(b)所示。

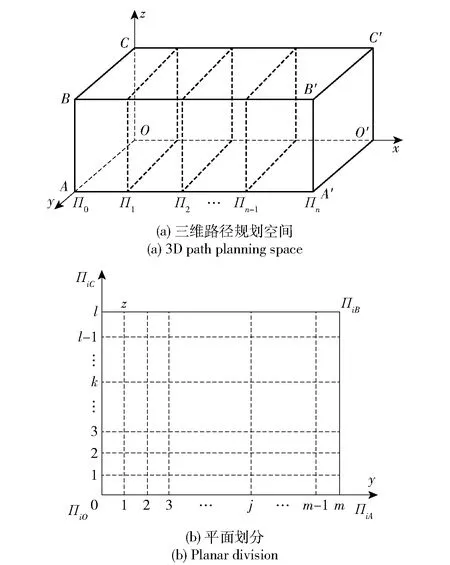
图1 三维空间抽象建模Fig.1 Three-dimensional abstract modeling

1.2 路径生成规则

首先，规定着陆车搜索的可行点，以保证其安全爬行于海底表面。着陆车从当前节点搜索至下一可行节点时，如果节点位于海底地形坡面，则该节点视为可行点(即安全点)；其次，设置可达区域，以减少算法复杂度，具体可达区域设计如下：以轴为前进方向，着陆车每向前爬行一步，允许最大横移为max，最大爬坡或下坡高度为max。

着陆车坐于海底后，通过所携带的超短基线水声定位获得其初始位置点，操作员使用上位机通过水声通信设置着陆车终点，着陆车控制系统在预先导入该海域三维海底环境的程序中载入起点、终点坐标，执行路径规划：着陆车从起点出发，首先到达平面可达域的某一可行点，然后从该点出发到达可达域的某一可行点，依次运行至最后平面终点，连接起点与终点之间经过的每一个网格点形成一条规划路径，如图2所示。

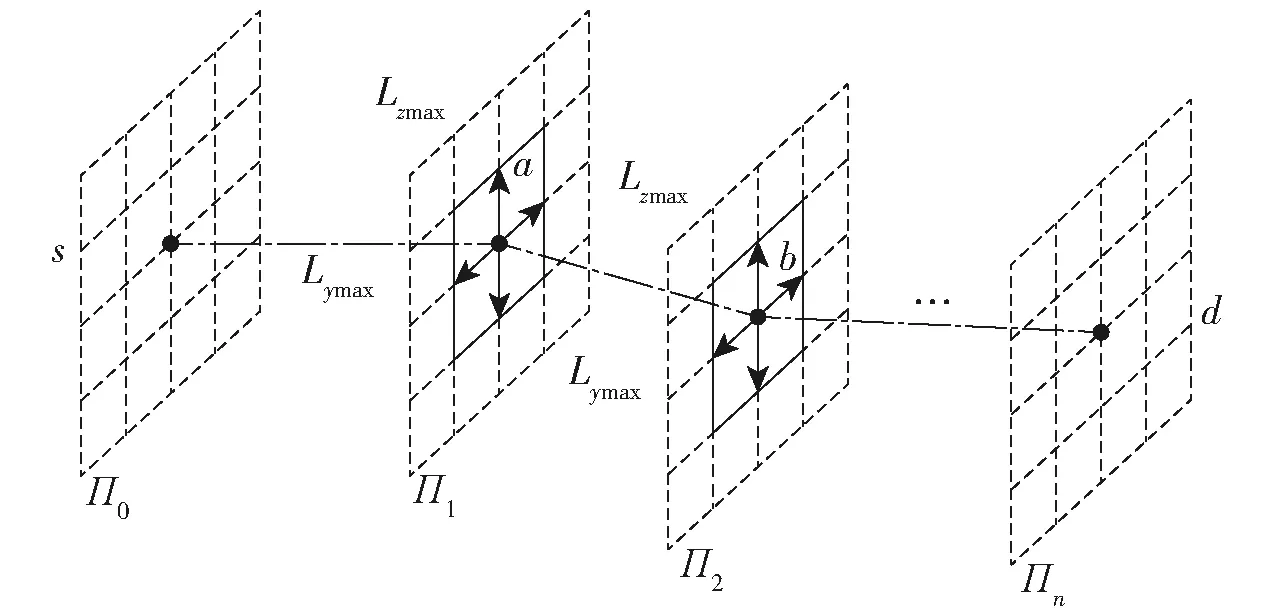
图2 路径点选取规则Fig.2 Waypoint selection rules

2 能耗计算方法

2.1 行驶阻力计算

深海着陆车航行于环境恶劣的深海，行驶阻力除了由海流引起的流体阻力外，还将受到来自履带底盘系统引起的内摩擦阻力，各轮转动过程中与履带接触及履带卷绕过程产生的阻力，以及深海着陆车在海底底质作业过程中土壤受履带挤压而产生的土壤压实阻力的水平分力。着陆车行驶受力如图3所示。图3中，为水阻力，为泥土阻力，为爬坡阻力，为驱动力，为支撑力，为海底坡度角，为着陆车航行时的行驶速度，为着陆车潜伏深海的负浮力质量，为重力加速度。

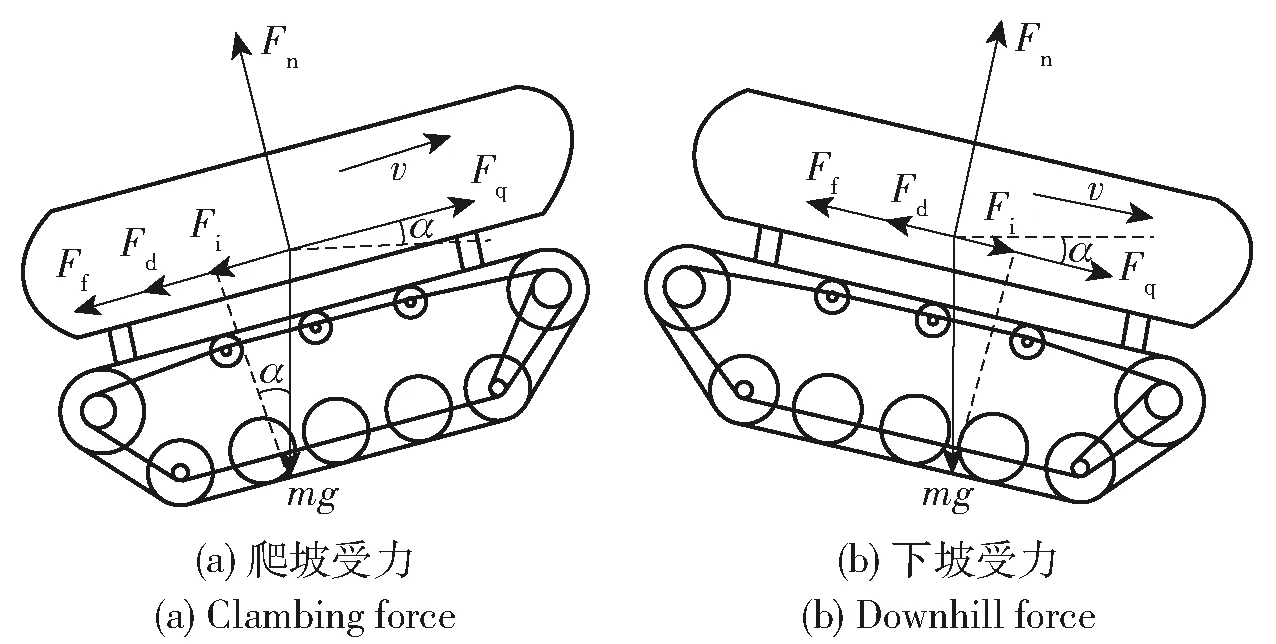
图3 着陆车航行时受力图Fig.3 Force diagram of landing vehicle during cruising

本文针对所在研究团队设计的深海着陆车样机航行时路径规划问题开展研究，着陆车主要技术参数见表1。

表1 主要技术参数Tab.1 Main technical parameters

211 水阻力

着陆车水下航行受到水阻力为

(1)

式中：为水动力系数；为海水密度。

212 泥土阻力

着陆车水下航行时受到泥土阻力为

=···cos

(2)

式中：为泥土阻力系数。

213 爬坡阻力

着陆车水下航行受到爬坡阻力为

=··sin

(3)

由表2参数，则行驶阻力为

表2 阻力参数Tab.2 Resistance parameters

=++=
2+···cos±··sin=
538125+98cos±392sin

(4)

式中：±表示着陆车爬坡与下坡时受到的阻力。由(4)式可知，当行驶阻力≥0 N时，表示着陆车受到的合阻力与其前进方向相反，阻碍着陆车运动；当行驶阻力<0 N时，表示着陆车受到的合阻力与其前进方向相同，此时合阻力将为着陆车提供动力。

2.2 电机效率建模

本文着陆车采用双侧直流无刷电机后驱方式，通过差动原理控制其运动。电机选用美国科尔摩根公司生产的TBM(S)型无框力矩电机，该电机为三相两级绕组接无刷直流电机。由无刷直流电机机械特性可知，在一定转速范围内，电机随转速提高机械效率逐渐提高，而无刷直流电机转速又决定着陆车航行速度。在着陆车匀速航行时，考虑着陆车自身传递效率、打滑率以及减速器传递效率，着陆车消耗在驱动电机的能量为着陆车克服行驶阻力、履带打滑、自身传递损耗和减速器损耗做功，因此电机效率也决定了着陆车工作效率。

搭建TBM-12941B电机测试平台，测得电机在任意转速、不同转矩下的机械输出效率关系如图4所示。经查其技术手册得知减速比为10∶1的减速器传递效率为93，着陆车在稀软海底上航行时打滑率13，以及考虑着陆车自身传递效率，则电机在额定转矩75 N·m下着陆车任意速度的工作效率曲线如图5所示。

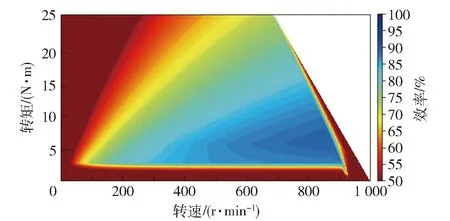
图4 电机转速、转矩与输出效率关系图Fig.4 Relation diagram of motor speed，torque and output efficiency

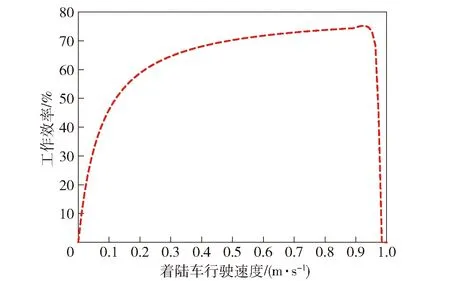
图5 着陆车速度与工作效率关系图Fig.5 Velocity and working efficiencyof landing vehicle

采用4次函数拟合图5散点线，得出着陆车航行速度(0 m/s<<095 m/s)与工作效率的函数为

=-16580+32548-
21955+6179+0031

(5)

2.3 能耗计算

忽略深海环境海流、着陆车航行时转弯、打滑、加减速等因素对能耗的影响，假设着陆车航行始终以匀速度从起始点出发，经过爬坡越障最终行驶至终点。着陆车匀速航行消耗能量为

(6)

式中：为着陆车到达终点行驶的里程。

将(4)式、(5)式代入(6)式，得

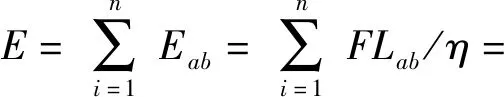
(7)

式中：为着路车到达终点所遍历的节点数；表示从当前点到下一可行节点的能源消耗；表示当前点到下一可行节点的距离。

由(7)式可知，航行时着陆车能耗仅与行驶速度、里程、地形坡度有关。根据(7)式可得如图6和图7所示单位里程能耗关系。

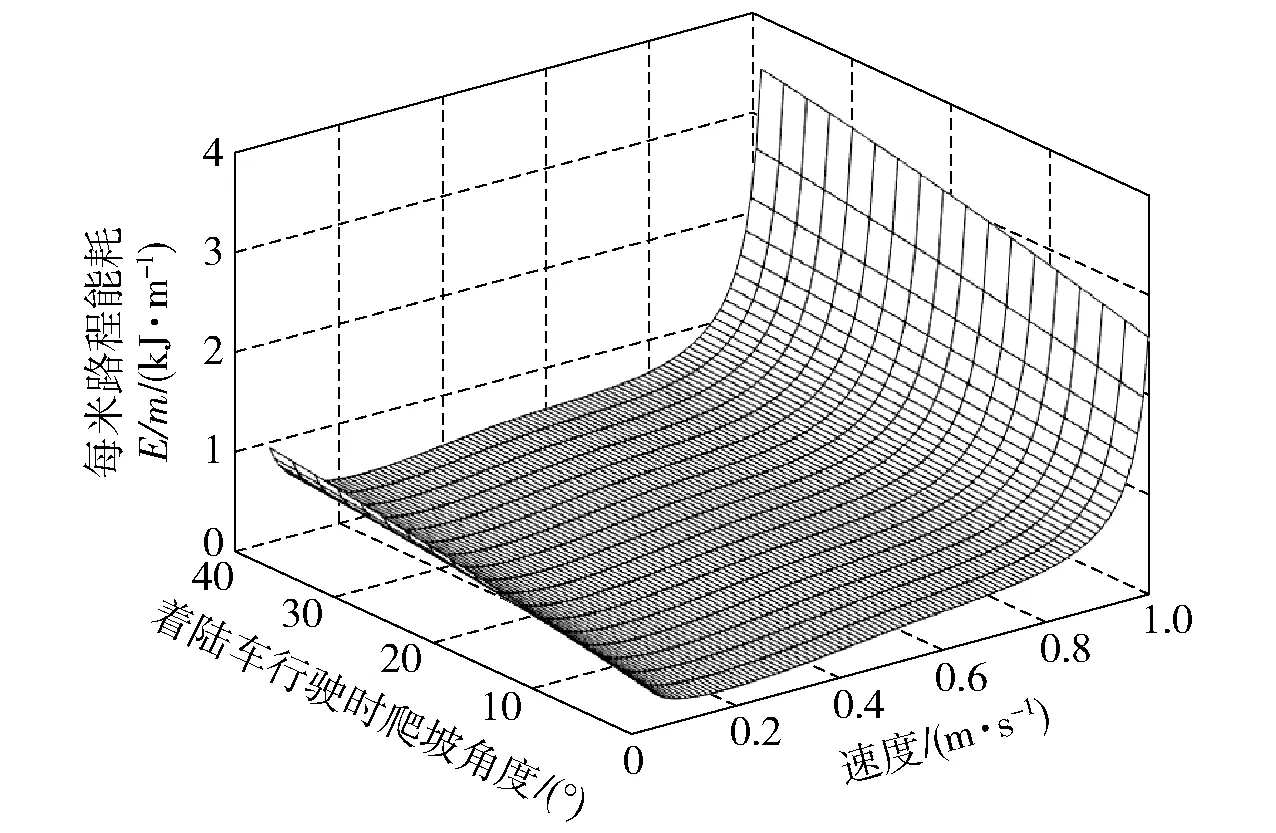
图6 爬坡时速度、坡度和能耗关系图Fig.6 Relationship between speed，slope and energy consumption during climbing

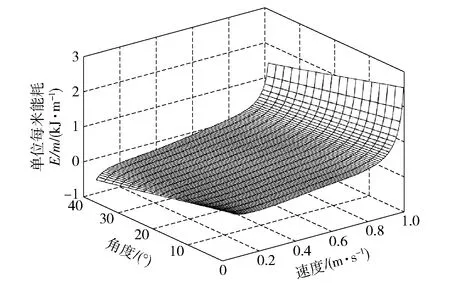
图7 下坡时速度、坡度和能耗关系图Fig.7 Relationship between speed，slope and energy consumption during going downhill

由图6和图7可知：当着陆车爬坡时，单位里程能耗随爬坡角度、车速的增加而增加，其中车速对着陆车能耗影响较大；下坡时，着陆车单位里程能耗虽然随下坡角度增大而降低，但车速增加着陆车能耗依然增加。依据(7)式，综合考虑深海着陆车工作的安全性、效率与能耗，将车速设定为05 m/s，爬坡角度限制在30°以内。

3 蚁群算法路径规划

3.1 信息素更新

蚁群算法使用信息素诱导蚂蚁搜索下一可行节点。由于仅采用全局信息素更新方式的传统蚁群算法，正反馈机制存在算法易陷入局部最优的缺点，本文采用局部信息素和全局信息素更新方式，通过局部信息素更新，使蚂蚁有更大概率选择上轮搜索路径之外的可行节点，同时限制信息素值区间，增强算法全局寻优能力，具体更新规则如下：

局部信息素更新是指蚂蚁从节点到达下一节点后，对该段路径信息素更新，公式为

()=(1-)(-1)

(8)

式中：()为时刻路径上的信息素值；为局部信息素衰减系数。

蚁群完成第次迭代后，通过评价函数对全局信息素进行更新，公式为

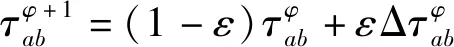
(9)

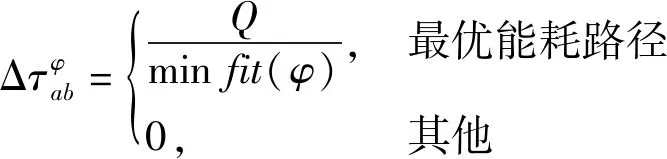
(10)

式中：为全局信息素衰减系数；为信息素浓度常数；()为第次迭代蚁群找到最佳路径的评价函数。另外，每个节点信息素值限定在[,]之间，用以避免算法过早收敛，用以避免算法扩散。

3.2 启发函数设计

蚁群算法使用信息素和启发函数进行转移概率计算来决定蚁群的路径选择。在时刻蚂蚁从当前节点到达下一节点的转移概率公式为

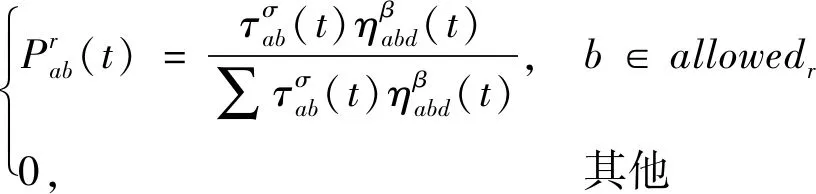
(11)

式中：()为启发函数；、分别为信息素和启发信息权重；为蚂蚁从点到下一步可达域内可行点点集。

本文启发函数设计考虑局部距离、全局距离、安全性和路径能耗4个因素，启发函数设计如下：

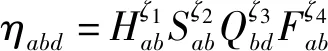
(12)

式中：为当前点到下一点路径长度的倒数值；为安全性因素，当选择为可行节点时值为1，否则为0；为下一点到目标点路径长度的倒数值；为当前点到下一点能耗的倒数值；、、、分别为相应权重。

1) 局部距离启发信息：促使蚁群选择距离最短的点，计算公式如下：

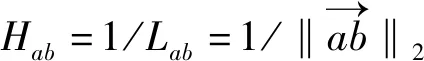
(13)

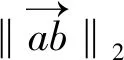
2) 安全性启发信息：使得蚁群选择可达域内的可行点，计算公式如下：

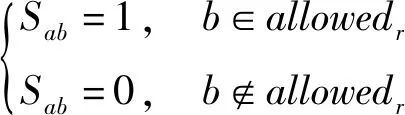
(14)

3) 全局距离启发信息：使得蚁群搜索具有方向性，增强算法搜索速度，计算公式如下：

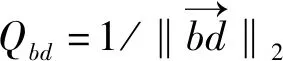
(15)

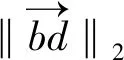
4) 路径能耗启发信息：使得蚁群选择低能耗的点，计算公式如下：

=1=1[(2+
···cos±··sin)/]

(16)

3.3 适应度函数设计

传统路径规划多以最短路径作为规划目标。然而，着陆车路径规划过程中不仅考虑路径长度，还要考虑能耗和运行时间等，为此本文提出能耗- 距离路径规划算法，即采用加权的方法，在保证着陆车安全行驶的同时实现路径里程与能耗问题的均衡，设计如下适应度函数：

()=()+()

(17)

式中：()和()为蚂蚁第次迭代路径总长度和总能耗因素；、为相应权重。下面分别对路径长度和能耗进行讨论。

1) 路径总长度因素：反映了算法对最短路径的追求，设计如下：

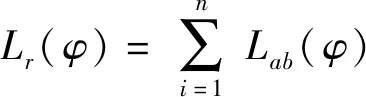
(18)

2) 路径总能耗因素：反映了算法对低能耗的追求，设计如下：

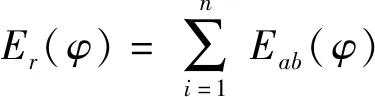
(19)

3.4 蚁群算法路径规划步骤

三维环境建模。导入三维海底数据及起点和终点坐标，对着陆车工作空间进行抽象建模与划分。

参数初始化。初始化信息素权重，信息素浓度常数，启发信息权重，启发函数系数、、、，信息素衰减系数，评价函数权重、，初始信息素，蚂蚁数量只，最大迭代次数。

蚁群搜索最优路径。依据(11)式计算蚂蚁从当前节点到达下一可行节点的转移概率值，只蚂蚁根据转移概率值依次从起点处出发搜索下一个可达域内的可行节点。

更新局部信息素值。每次蚂蚁到达下一个可行节点后，按(8)式进行局部信息素值更新。

每代蚁群找出的最佳路径。第次迭代只蚂蚁完成一次搜索后，根据(17)式对当代蚁群经历的所有路径进行评价，保存最佳评价值和最佳路径的所有节点。

更新全局信息素值。对所有节点按(9)式和(10)式进行全局信息素值更新。

完成路径规划。每迭代一次迭代器加1，若未达到，则重复步骤1～步骤6。最终得到最优路径。

4 算法仿真及分析

为验证能耗- 距离路径规划算法的有效性，本文将10 km×10 km×50 m的三维海底模型划分为100×100×50大小相同的栅格，设置相同起始点和终点进行多次仿真，仿真参数见表3。

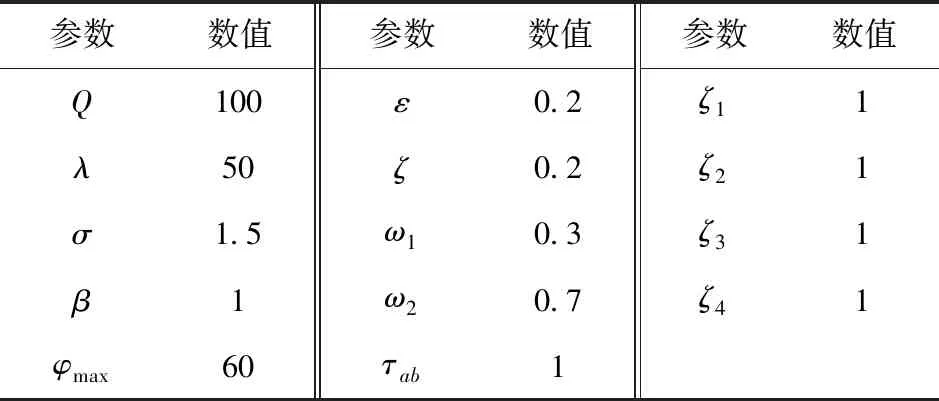
表3 仿真参数取值Tab.3 Simulation parameter selection

在MATLAB 2018a软件环境中，分别用传统路径最短、传统能耗最低和路径能耗- 距离优化3种方案进行50次仿真。其中某次3种方案路径规划结果如图8所示，50次仿真路径长度与能耗对比分别如图9和图10所示，仿真数据平均值统计结果见表4。

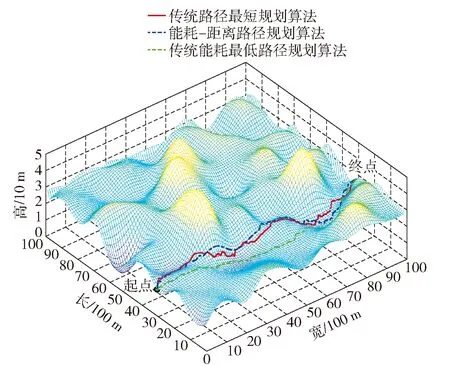
图8 路径规划结果Fig.8 Path planning results

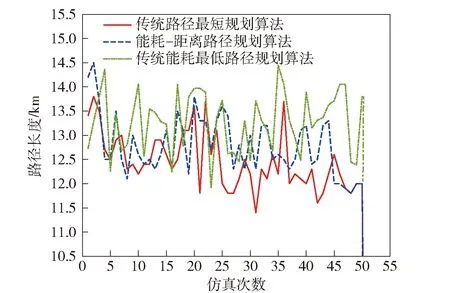
图9 路径长度对比图Fig.9 Path length comparison chart

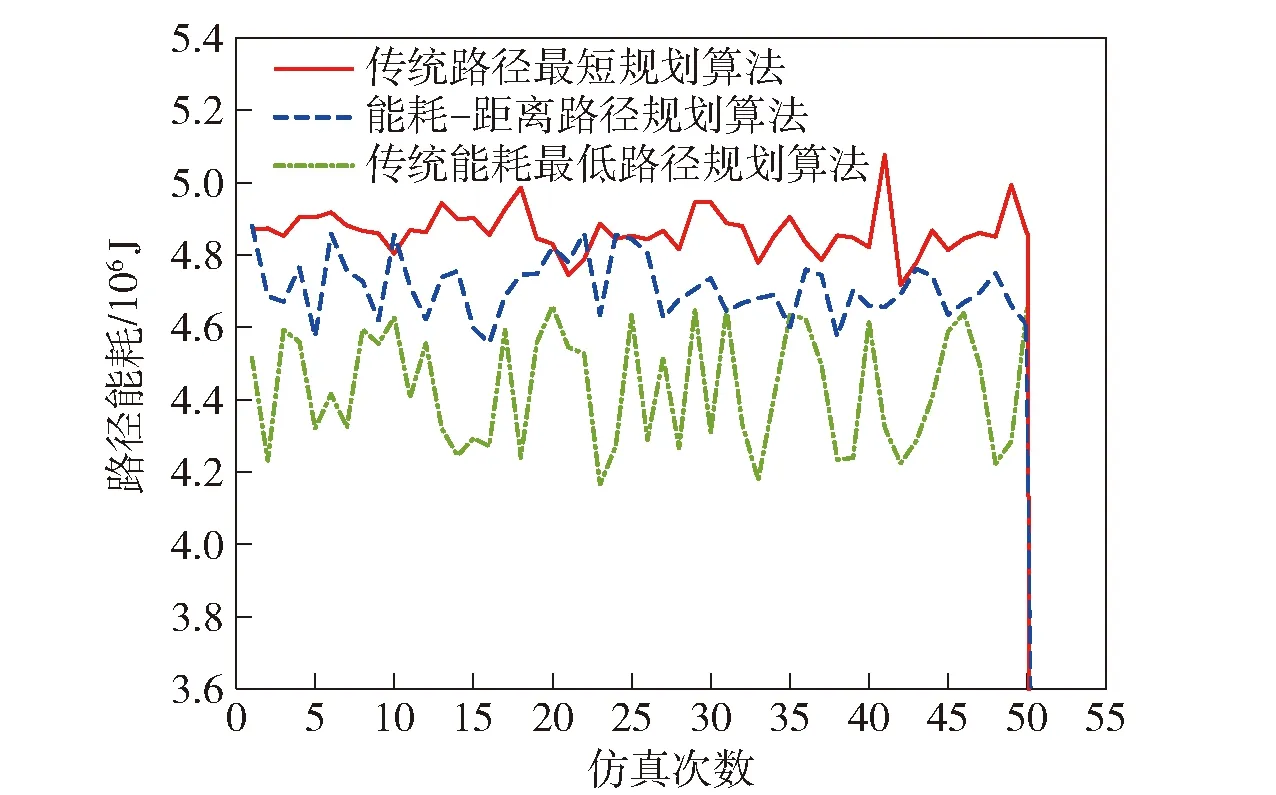
图10 路径能耗对比图Fig.10 Path energy consumption comparison chart

表4 3种算法仿真数据统计对比Tab.4 Statistical comparison of algorithm simulation data

在匀速运动情况下，作业时间与路径长度呈正比。根据深海着陆车作业需求，本文算法通过合理选取路径权重和能耗权重来均衡作业的里程与能耗。仿真结果表明：本文能耗- 距离路径规划算法相对于传统路径最短规划算法，其搜索效率提升2581，路径长度虽增加400，但能耗却降低673；相对于传统能耗最低路径规划算法，能耗- 距离路径规划算法搜索效率提升1154，能耗虽增加了386，但路径长度却减少226。以上结果表明，本文算法在实际应用中通过合理选取评价函数权重参数，能有效均衡着陆车航行时能源消耗与作业里程，可以很好满足着陆车长续航作业需求。