SiC陶瓷/UHMWPE纤维复合结构抗12.7 mm穿甲燃烧弹试验与仿真
2022-07-05李永鹏徐豫新张健花培鑫赵晓旭
李永鹏,徐豫新,2,3,4,张健,花培鑫,赵晓旭
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.高能量密度材料教育部重点实验室,北京 100081;3.北京理工大学 北京理工大学重庆创新中心,重庆 401120;4.北京理工大学 唐山研究院,河北 唐山 063000;5.北京理工大学 机电学院,北京 100081;6.首都师范大学 信息工程学院,北京 100048)
0 引言
防护结构轻量化是武器装备的一个重要发展方向,高强、低密度材料的应用及结构整体的优化设计是实现结构轻量化的主要途径。目前轻金属合金、陶瓷、纤维增强复合材料等轻质材料广泛应用于抗弹结构。通常通过对上述轻质材料组成复合结构的合理设计,充分发挥不同材料各自的优势,实现结构整体抗弹体侵彻性能的提升。
长期以来,国内外就轻金属合金、陶瓷和纤维增强复合材料组合而成的防护结构抗弹性能及机理进行了大量研究。Zou等、Wang等、Gao等和刘国繁等通过试验和数值仿真研究了陶瓷、超高分子量聚乙烯(UHMWPE)及TC4钛合金组合而成复合结构的抗弹吸能机制,并研究了各组元厚度对结构整体抗弹性能的影响规律。Shen等通过试验和数值仿真,系统研究了弹体形状对UHMWPE抗侵彻性能的影响,并详细分析了不同形状弹体侵彻下UHMWPE的变形过程、失效机制和吸能性能。陈智勇等研究了SiC木质陶瓷厚度、形状、尺寸和布局等对SiC陶瓷/UHMWPE纤维复合结构抗弹性能的影响规律。刘桂武等通过侵彻试验研究了约束方式对复合结构抗侵彻性能的影响规律。胡丽萍等研究了陶瓷厚度、倾角和约束条件等对大倾角陶瓷复合装甲抗弹性能的影响规律。Hu等研究了弹体侵彻下韧性金属/陶瓷/UHMWPE/韧性金属复合结构的破坏模式以及陶瓷层布置、陶瓷层与UHMWPE层间质量分配对弹道性能的影响。
综上所述,现有弹体对陶瓷复合结构的侵彻研究主要集中在复合结构的破坏模式以及陶瓷板约束方式、动能弹侵彻角度、陶瓷块形状和面积等对抗侵彻性能影响规律方面,对于组元厚度比对其抗弹性能影响的研究鲜有报道。
本文针对SiC陶瓷板、UHMWPE纤维板层合而成的复合结构,进行12.7 mm穿甲燃烧弹侵彻试验,获得不同侵彻速度下复合结构的防护效果。建立了弹体对SiC陶瓷/UHMWPE纤维复合结构侵彻有限元计算模型,通过试验结合数值仿真,分析复合结构的破坏机制,掌握SiC陶瓷板、UHMWPE纤维板厚度对复合结构抗弹性能的影响规律,为SiC陶瓷/UHMWPE纤维复合结构优化设计提供支撑。
1 弹体侵彻试验
1.1 试验系统及弹、靶材料
采用12.7 mm弹道枪加载弹体对SiC陶瓷/UHMWPE纤维复合结构进行侵彻试验,试验系统及现场布置如图1所示。SiC陶瓷与UHMWPE纤维板通过固化粘合剂进行粘结后,采用工字夹固定于靶架,靶前后放置通断测速靶,用于测量着靶速度和弹体穿透靶板后的剩余速度,并采用高速摄影机捕获弹体对复合结构侵彻过程。
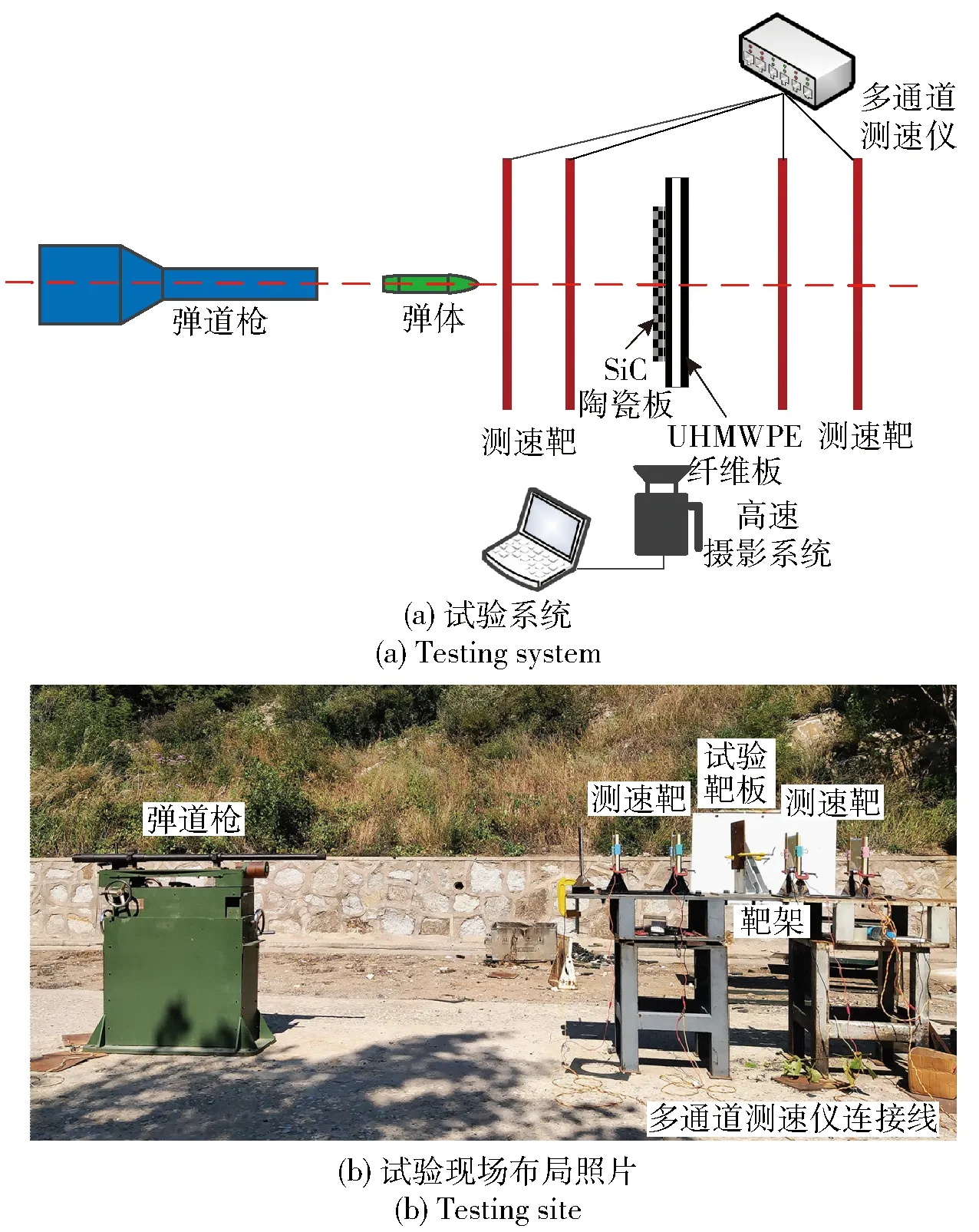
图1 弹道枪试验系统及现场照片Fig.1 Testing system and site for for ballistic rifle
试验所用复合结构如图2所示。其中,SiC陶瓷板为迎弹面,密度为3.13 g/cm,尺寸为100 mm×100 mm×6 mm。UHMWPE纤维板为背弹面,UHMWPE纤维板由UD布叠层压制,密度为0.97 g/cm,纤维板尺寸为150 mm×150 mm×10 mm。

图2 试验用复合结构Fig.2 Composite structure for test
1.2 试验结果及分析
试验通过改变发射药量调整弹体发射速度,共进行10发,试验结果列于表1中。
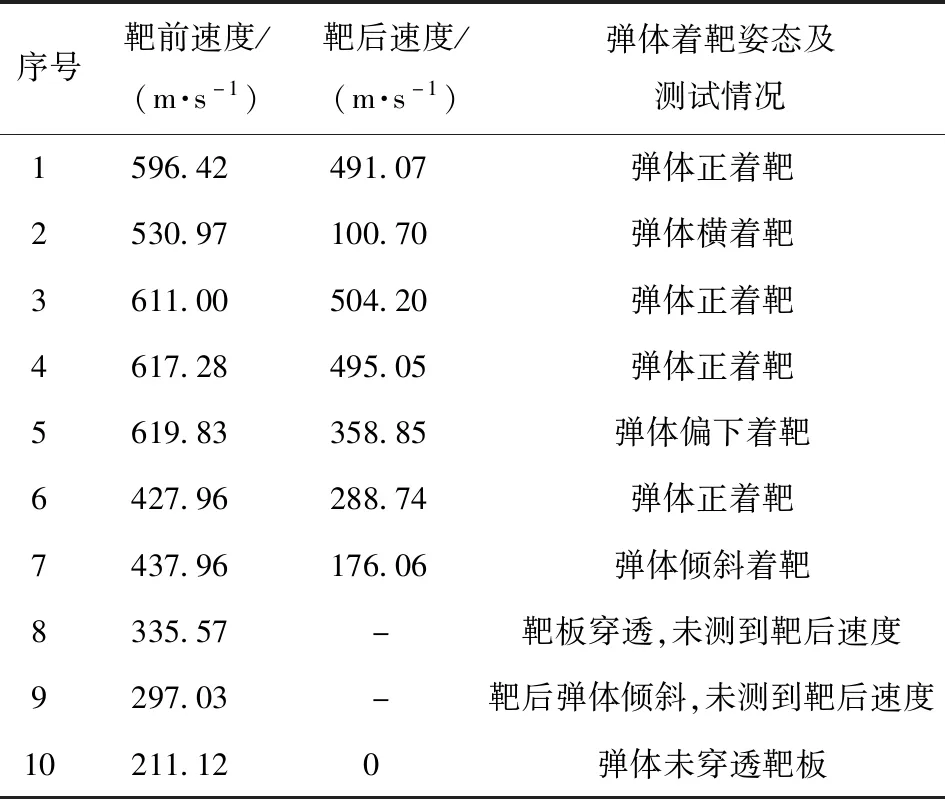
表1 试验结果Tab.1 Test results
试验8(335.57 m/s撞击速度)弹体侵彻靶板过程如图3所示,试验后UHMWPE纤维板破坏形貌如图4所示。由图3可见,弹体在穿透靶板后向下偏转,同时陶瓷板破碎,形成碎块向前飞溅。结合图4可知,UHMWPE纤维板因受到弹体冲击向后弯曲并凸起,在此过程中粘结层逐渐失效,剥离面积增大,形成分层破坏。同时,弹体着靶时燃烧剂引燃纤维丝,降低了纤维板的抗侵彻能力。弹体贯穿靶板过程中,被引燃的纤维板中心由于弹体剪切作用形成方形破口,纤维板四周由于纤维层凸起而向内紧缩,此现象与文献[11]中的现象一致。

图3 弹体侵彻靶板历程(v=335.57 m/s)Fig.3 Process of projectilepenetrating into the target (v=335.57 m/s)

图4 UHMWPE纤维板典型破坏形貌(v=335.57 m/s)Fig.4 Typical damage morphology of UHMWPE fiberboard(v=335.57 m/s)
2 数值仿真
2.1 几何模型及离散化
选用cm-g-μs-Mbar单位制建立弹靶系统1/4模型。弹体侵彻复合结构时,由于披甲与弹芯迅速脱离,侵彻作用较小,弹芯起主要侵彻作用,仿真时只考虑弹芯对复合结构作用。弹芯头部为尖卵形,详细尺寸如图5(a)所示,根据弹芯尺寸建立模型并进行离散化,所建立模型的最小网格尺寸为0.3 mm,如图5(b)所示。
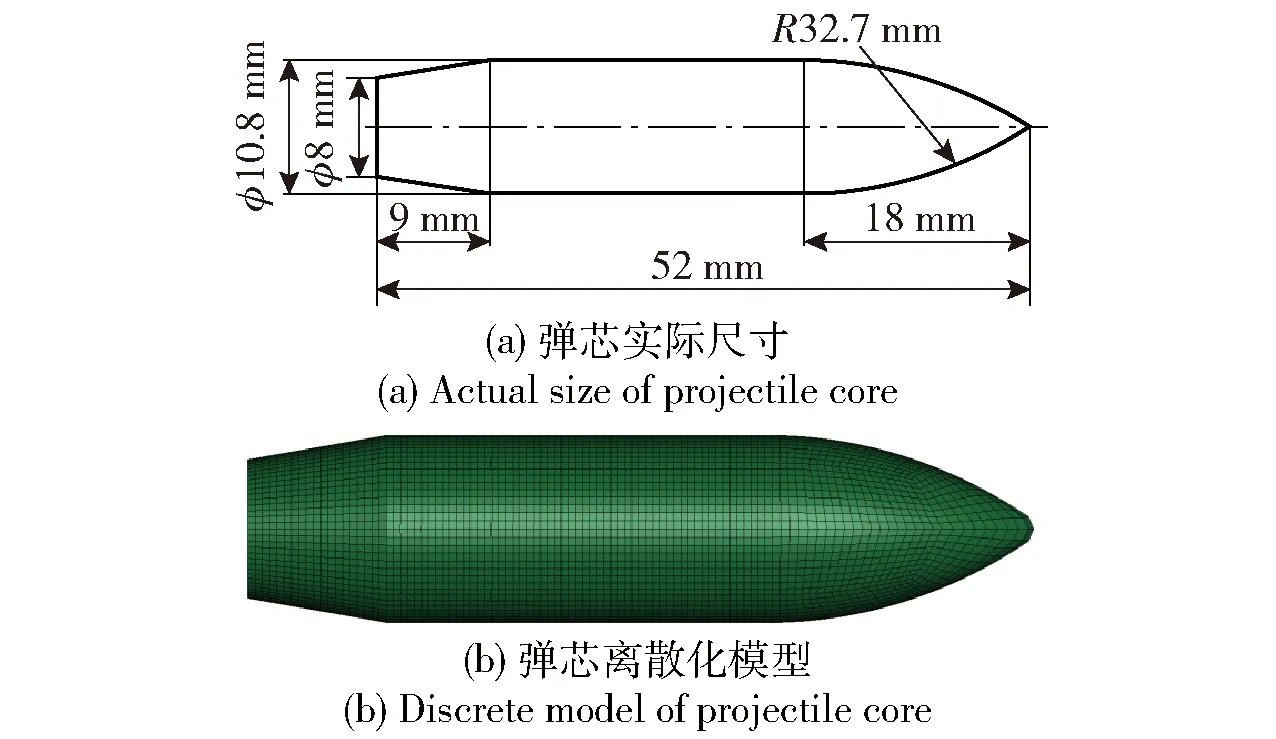
图5 12.7 mm穿甲燃烧弹弹芯尺寸及数值仿真模型Fig.5 Core size and numerical simulation model of 12.7 mm API projectile
采用8节点Solid164三维实体单元和4节点Shell163薄壳单元分别建立SiC陶瓷板和UHMWPE纤维板数值仿真模型。为模拟纤维板分层失效,在建模时将整块纤维板等效为多层板,设置每层厚为0.5 mm。为提升计算精度,对侵彻区域网格进行局部加密,陶瓷和纤维板的最小网格尺寸分别为0.3 mm和0.6 mm。整体模型如图6所示。

图6 有限元模型Fig.6 Finite element model
2.2 材料模型及参数
弹芯材料为高强度合金钢,选用Johnson-Cook材料模型和Grüneisen状态方程予以描述,具体材料参数列于表2中。SiC陶瓷板采用JH-2模型予以描述,SiC陶瓷材料的强度、刚度属性、损伤常数和状态方程参数列于表3中。
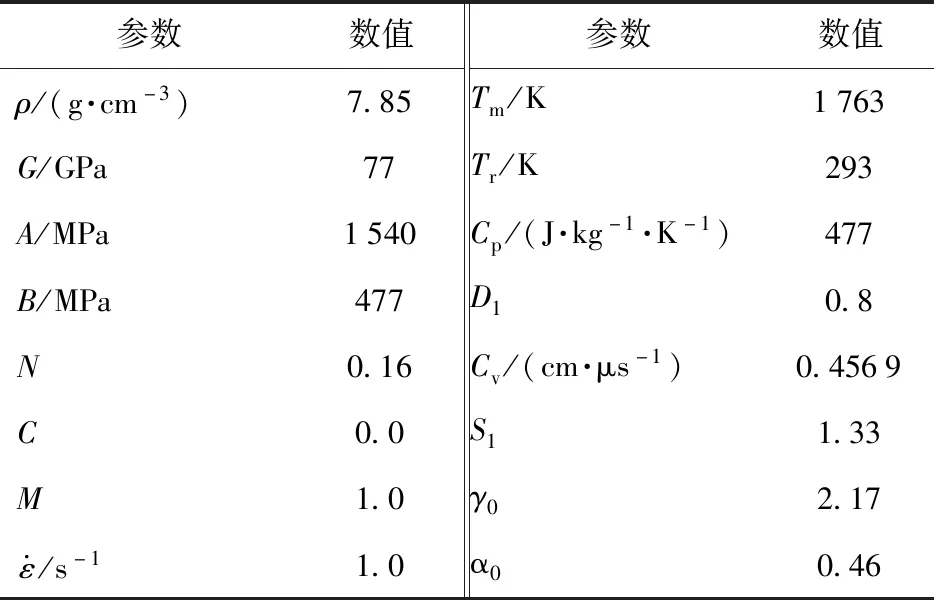
表2 弹芯钢材料参数Tab.2 Projectile core material parameters
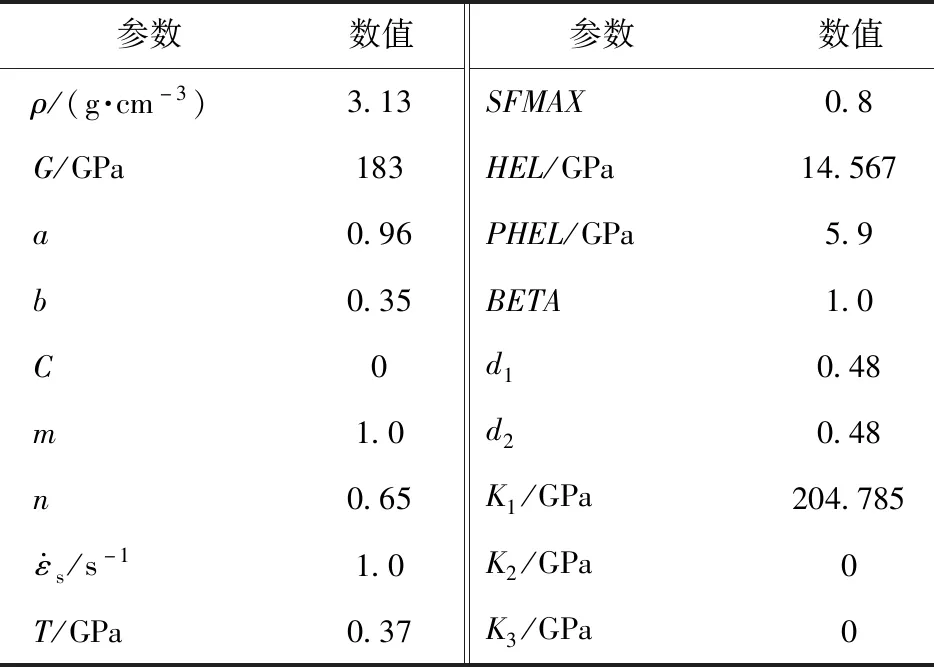
表3 SiC陶瓷板材料参数[17]Tab.3 SiC ceramic material parameters[17]
UHMWPE纤维板属于层合结构,选用基于Chang-Chang失效准则的Enhanced-Composite-Damage(MAT_054)材料模型予以描述,部分材料参数列于表4中。此外,设置Enhanced-Composite-Damage模型中APOT=3,并结合PART-COMPOSITE关键字来定义UHMWPE纤维板中的纤维方向,如图7所示。
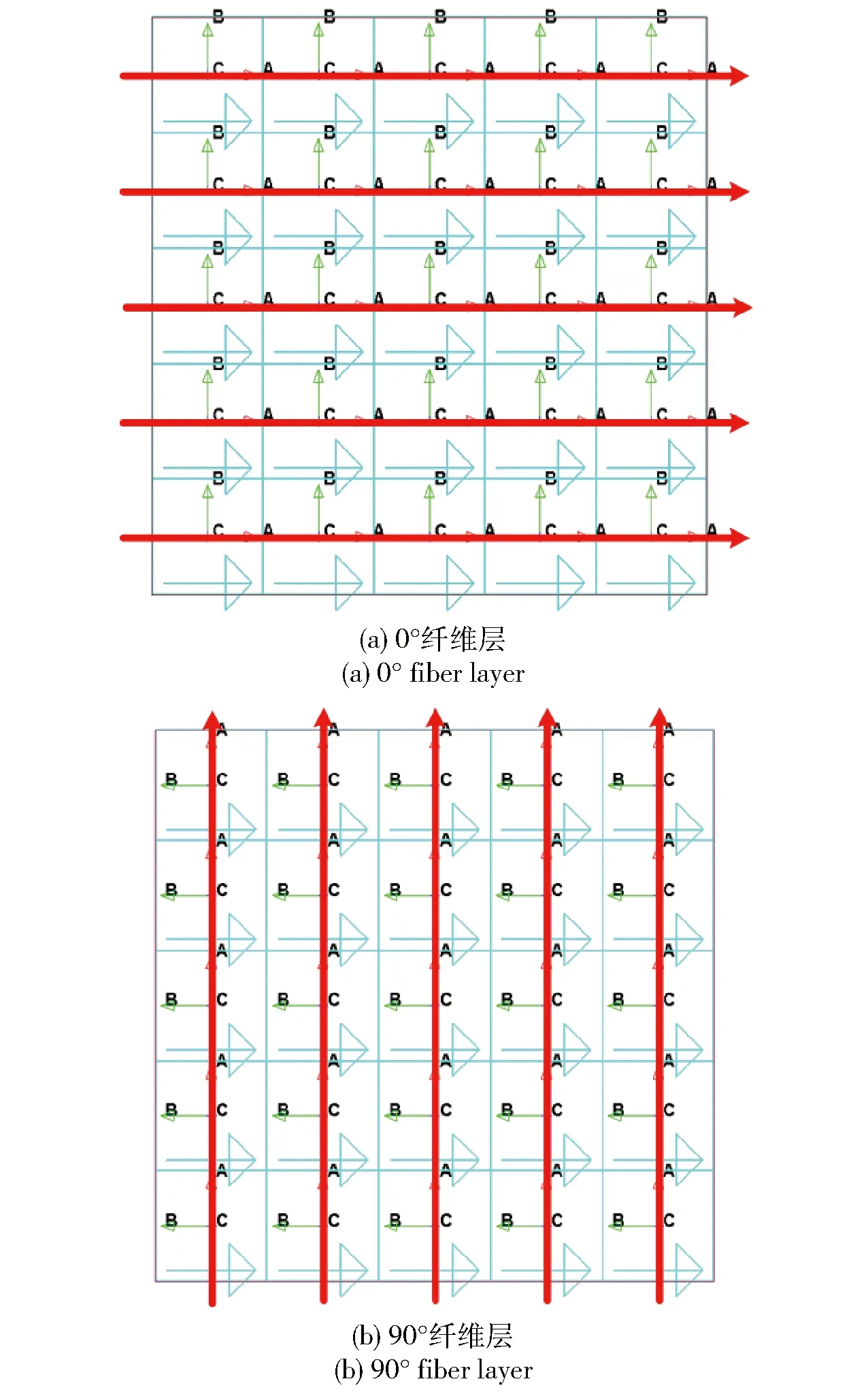
图7 UHMWPE离散层的不同角度铺层(蓝色箭头为单元方向,红色箭头为纤维方向)Fig.7 Different angles of UHMWPE discrete layer(blue arrow:grid direction;red arrow:fiber direction)
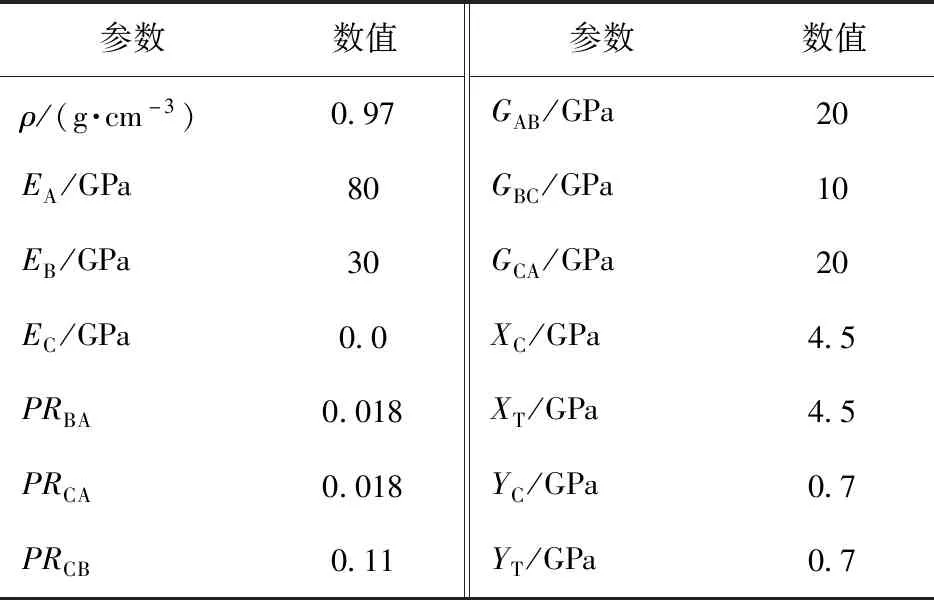
表4 UHMWPE纤维板材料参数[5]Tab.4 UHMWPE fiberboard material parameters[5]
弹体与各层靶板之间设置面面侵蚀接触。SiC陶瓷板与UHMWPE纤维板之间、UHMWPE纤维板各层之间均设置固连失效自动接触,纤维板四周施加固定约束,弹体施加初始速度后进行仿真计算。
2.3仿真结果及验证
为验证上述仿真方法的可靠性,对试验工况进行数值仿真计算,选取弹体正着靶的4发试验与仿真对比,列于表5中。由表5可见,采用上述模型计算出的弹体剩余速度与试验值误差最小为-3.22%,最大为2.49%,说明数值仿真中参数设置合理,仿真结果可信。
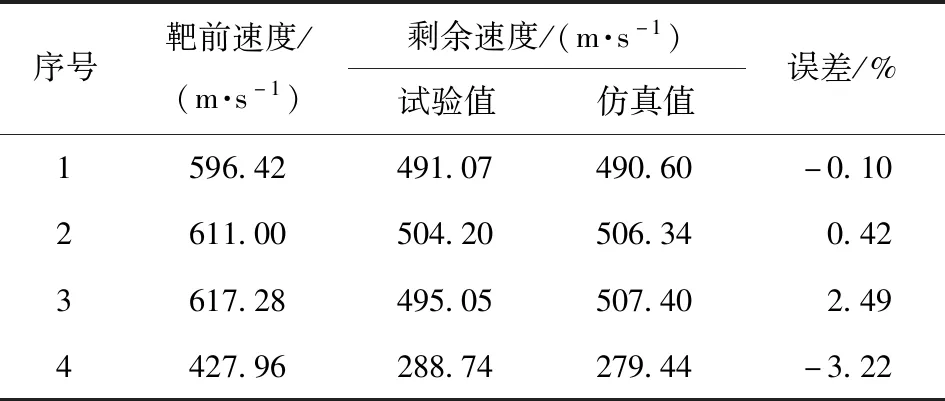
表5 剩余速度仿真值与试验值对比Tab.5 Simulated and test values of residual speed
2.4 抗侵彻机理分析
将弹体侵彻中复合结构破坏过程分为陶瓷裂纹产生和扩展、纤维板剪切破坏和纤维板弯曲破坏3个阶段,如图8所示。
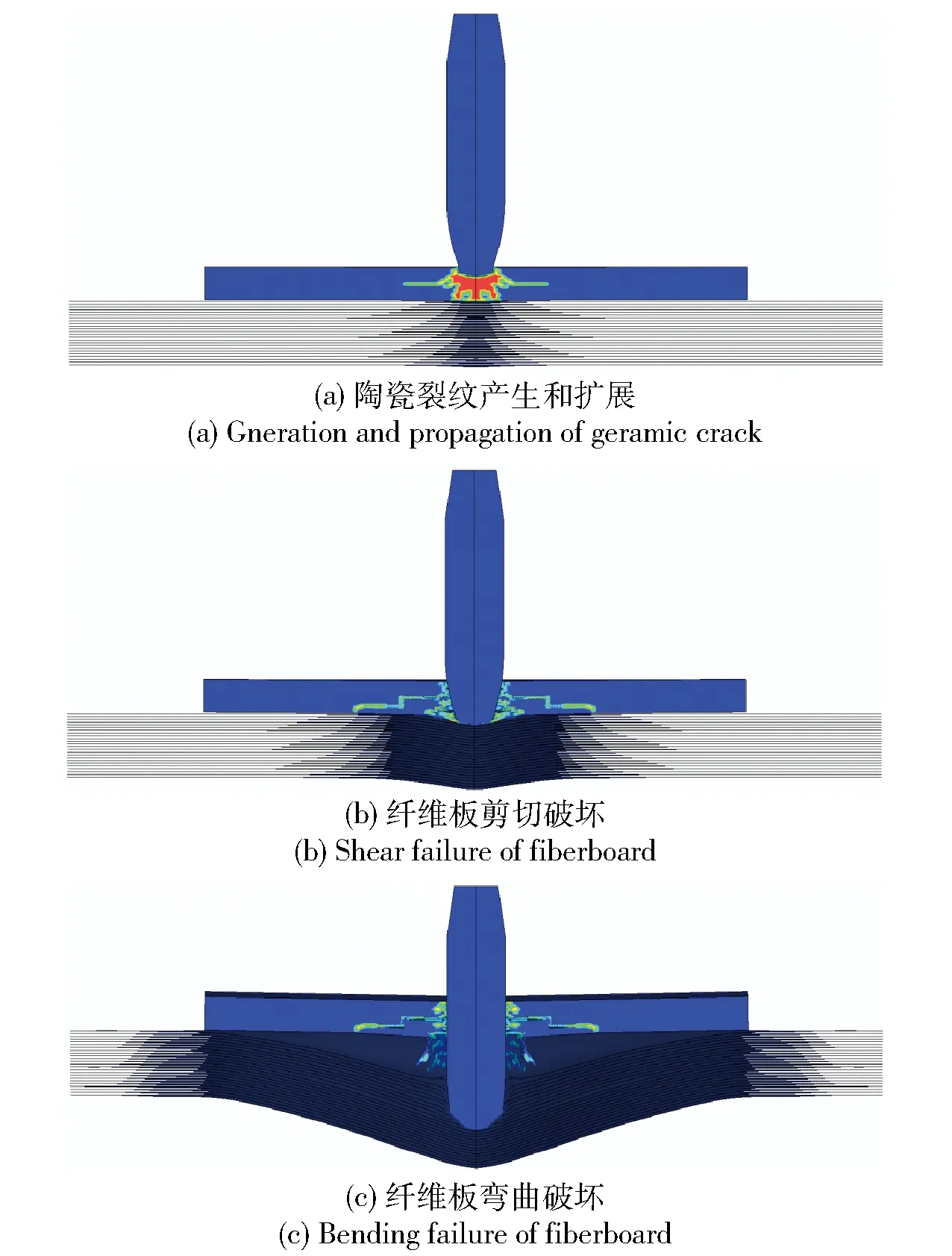
图8 弹体侵彻复合结构过程Fig.8 Process of projectile penetrating into composite structure
图8(a)为陶瓷裂纹产生和扩展阶段。此阶段弹体与陶瓷板相互作用,弹体动能大幅减小,陶瓷在压缩波作用下产生微裂纹。当压缩波传递到陶瓷板背部界面时,纤维板因受压缩降低了对陶瓷板的支撑作用,陶瓷板内部的压缩波变为拉伸波,微裂纹逐渐扩展成宏观裂纹。同时,剪应力和拉应力的共同作用使陶瓷沿着约70°方向破碎形成陶瓷锥,如图9所示。陶瓷锥可增大弹体对纤维板作用面积,避免纤维板的受力集中。
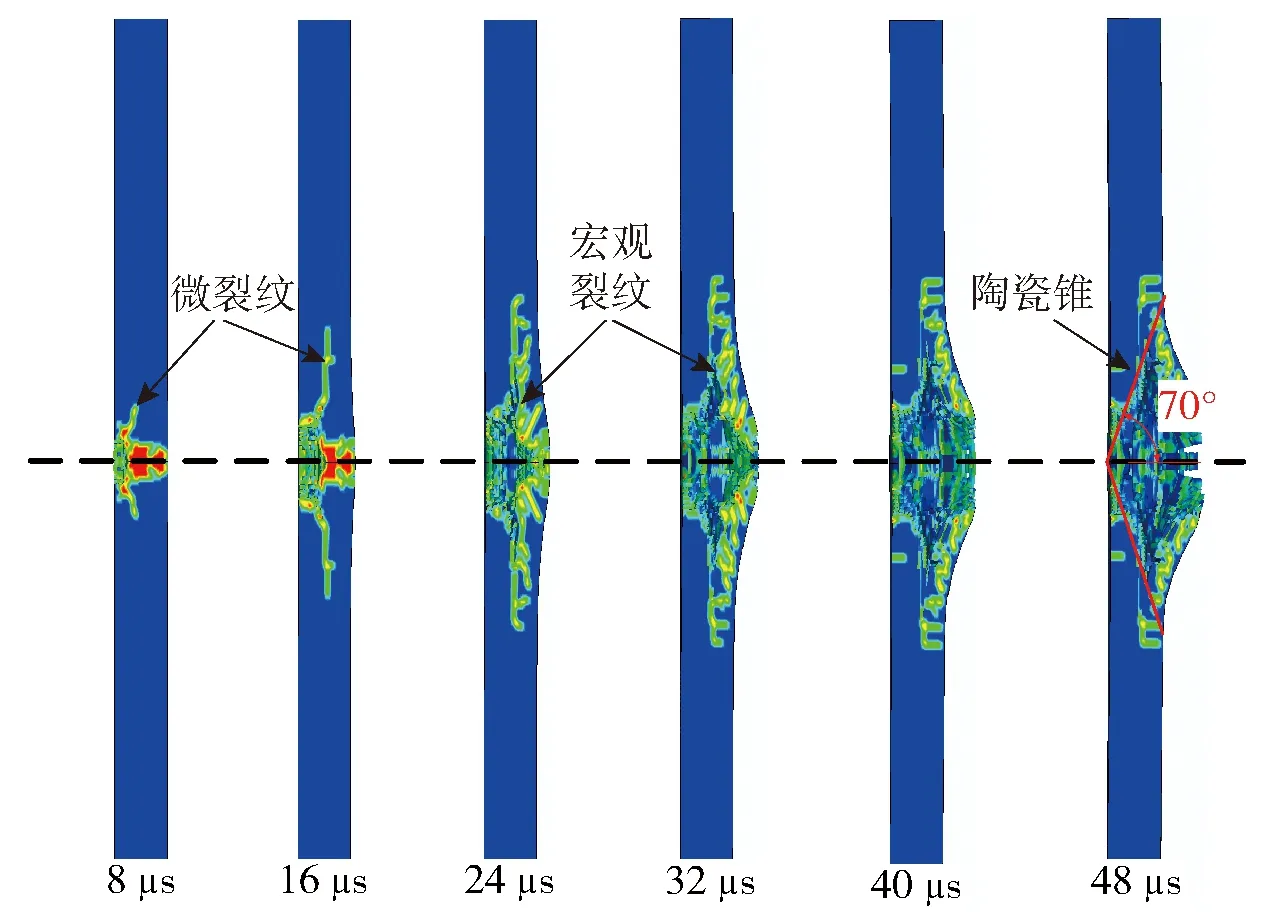
图9 陶瓷裂纹扩展及陶瓷锥的形成Fig.9 Ceramic crack propagation and ceramic cone formation
图8(b)为UHMWPE纤维板剪切破坏阶段。此阶段纤维板在应力波和陶瓷锥作用下已具一定初始速度和初始变形。弹体接触区和周围协变区之间存在明显速度差,迎弹面发生剪切破坏。各层纤维在弹体和陶瓷锥共同作用下发生弯曲变形,当应力大于纤维的极限应力时纤维层断裂。由于纤维板为正交铺层,背弹面表面形成沿纤维方向的近十字形凸起,如图10所示。

图10 UHMWPE纤维板背弹面的近十字形凸起Fig.10 “Cross-shaped” protrusions on the back surface of UHMWPE fiberboard
图8(c)为UHMWPE纤维板弯曲破坏阶段。该阶段弹体速度继续减小,迎弹面纤维板由于吸收弹体动能,速度逐渐增加,弹体和靶板之间速度差逐渐减小,相互作用时间增长,剪切作用逐渐减弱,纤维板的主要破坏模式由剪切破坏过渡为弯曲变形。另外,陶瓷锥的作用使纤维板受力面积不断增大,弯曲变形范围逐渐增大。纤维板大范围变形的同时,层间分层范围逐渐增大,形成明显的层裂现象,如图11所示。弹体持续侵入纤维板向前运动使凸起区域纤维层达到强度极限而断裂,直至贯穿纤维板。
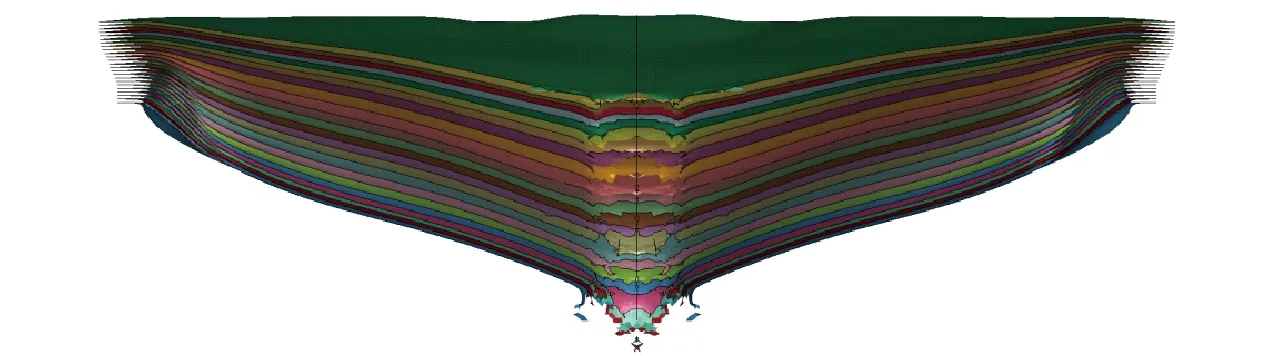
图11 UHMWPE纤维板的分层破坏Fig.11 Delamination failure of UHMWPE fiberboard
3 复合结构抗弹性能影响规律分析
3.1 复合结构抗弹性能与组元厚度相关性
复合结构抗弹性能与组元厚度密切相关。为研究复合结构抗弹性能与组元厚度的相关性,设计16组工况进行仿真,通过数值仿真研究弹道极限速度随SiC陶瓷板和UHMWPE纤维板厚度变化规律。计算结果列于表6中,其中和分别为SiC陶瓷板及UHMWPE纤维板的厚度。
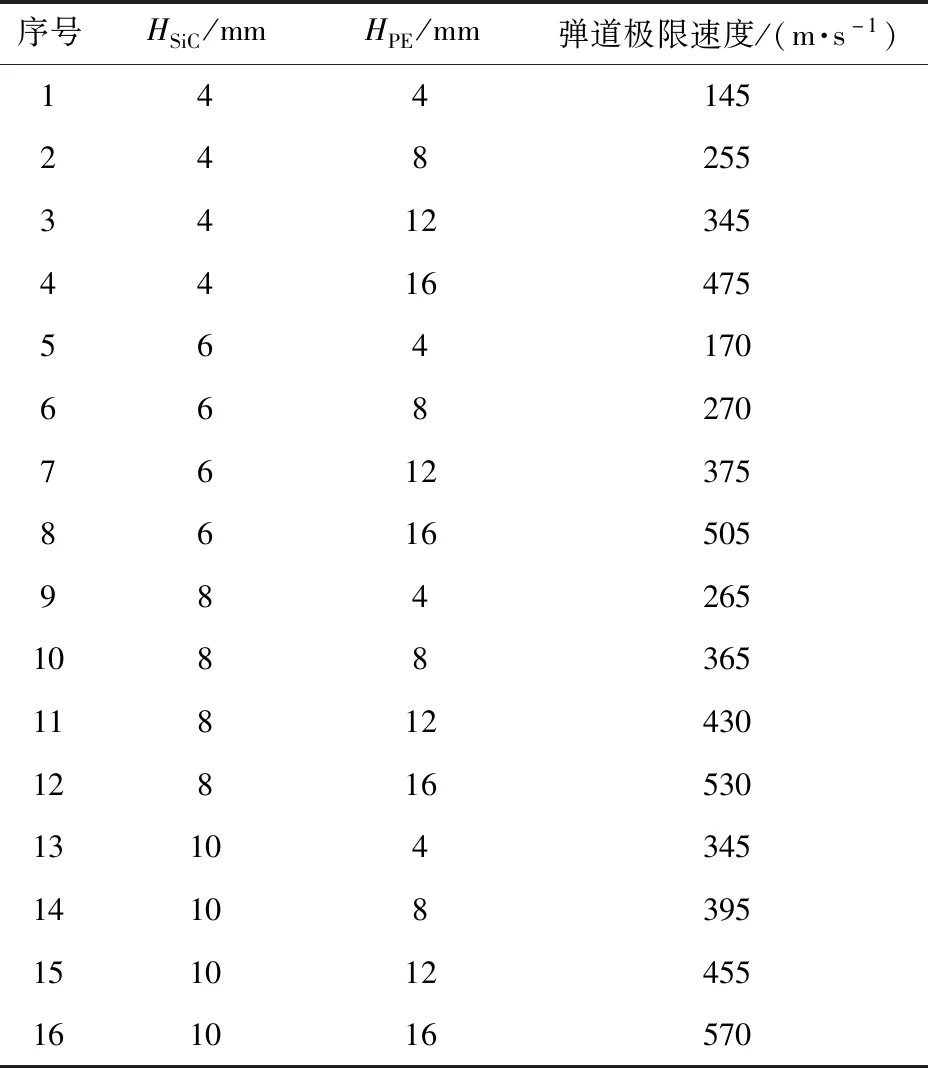
表6 弹体对复合结构侵彻的弹道极限仿真计算结果Tab.6 Simulated results of ballistic limit velocity of projectile penetrating into composite structure
根据表6中数据,得到弹道极限速度随SiC陶瓷板厚度和UHMWPE纤维板厚度曲线如图12所示。由图12可见,12.7 mm穿甲燃烧弹对复合结构的弹道极限速度分别随SiC陶瓷板和UHMWPE纤维板厚度的增加线性增加。用和分别表示图12中弹道极限速度与SiC陶瓷板厚度和UHMWPE纤维板厚度的比值,得到和随SiC陶瓷板和UHMWPE纤维板厚度增加的衰减规律曲线如图13所示。由图13可见:和随SiC陶瓷板和UHMWPE纤维板厚度的增加而逐渐减小,但二者的变化趋势存在明显差异;当SiC陶瓷板和UHMWPE纤维板厚度相同时,SiC陶瓷对复合结构抗弹性能的影响较UHMWPE纤维板大。
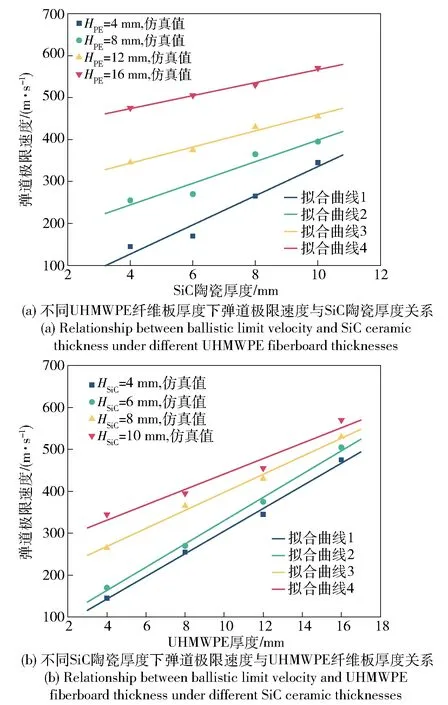
图12 弹道极限速度与各组元厚度关系Fig.12 Relationship between ballistic limit velocity and thickness of SiC ceramic layer
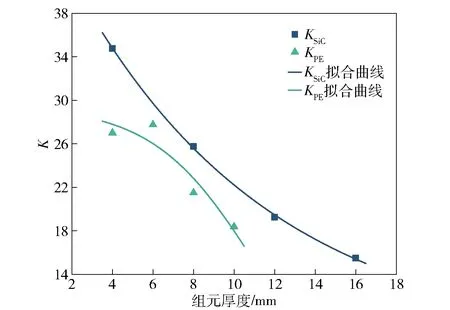
图13 弹道极限速度/厚度比值随SiC和UHMWPE厚度增加的衰减规律Fig.13 Attenuation law of ballistic limit velocity/thickness ratio with the increasein SiC and UHMWPE thickness
3.2 复合结构抗弹性能与组元厚度比相关性
为研究不同面密度下复合结构抗弹性能与组元厚度比的相关性,设置弹体初速度为620 m/s,选取5种不同面密度复合结构,共27组工况进行数值仿真计算。复合结构的吸能性能可用单位面密度吸收能来表征,
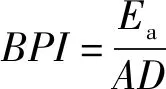
(1)
式中:为复合结构吸收能,本文中用弹体动能差来表征;为复合结构总面密度,=+,和分别为SiC陶瓷和UHMWPE纤维的密度。
通过数值仿真计算不同面密度和不同厚度比条件下的弹体剩余速度,并根据(1)式计算复合结构的,结果列于表7中。
根据表7中的数据,得到弹体剩余速度和单位面密度吸能随复合结构组元厚度比关系曲线如图14和图15所示。由图14和图15可见,随着SiC陶瓷与UHMWPE纤维板厚度比的增加,不同面密度复合结构弹体剩余速度均呈现出先减小后增大的趋势,而复合结构单位面密度吸能则均呈现出先增大后减小趋势。由此可见,随SiC陶瓷与UHMWPE纤维板厚度比的增加,复合结构的抗弹体侵彻性能先增强后减小,如图14和图15中蓝色区域所示,当厚度比在0.2~0.4之间时,复合结构抗弹体侵彻性能最佳。
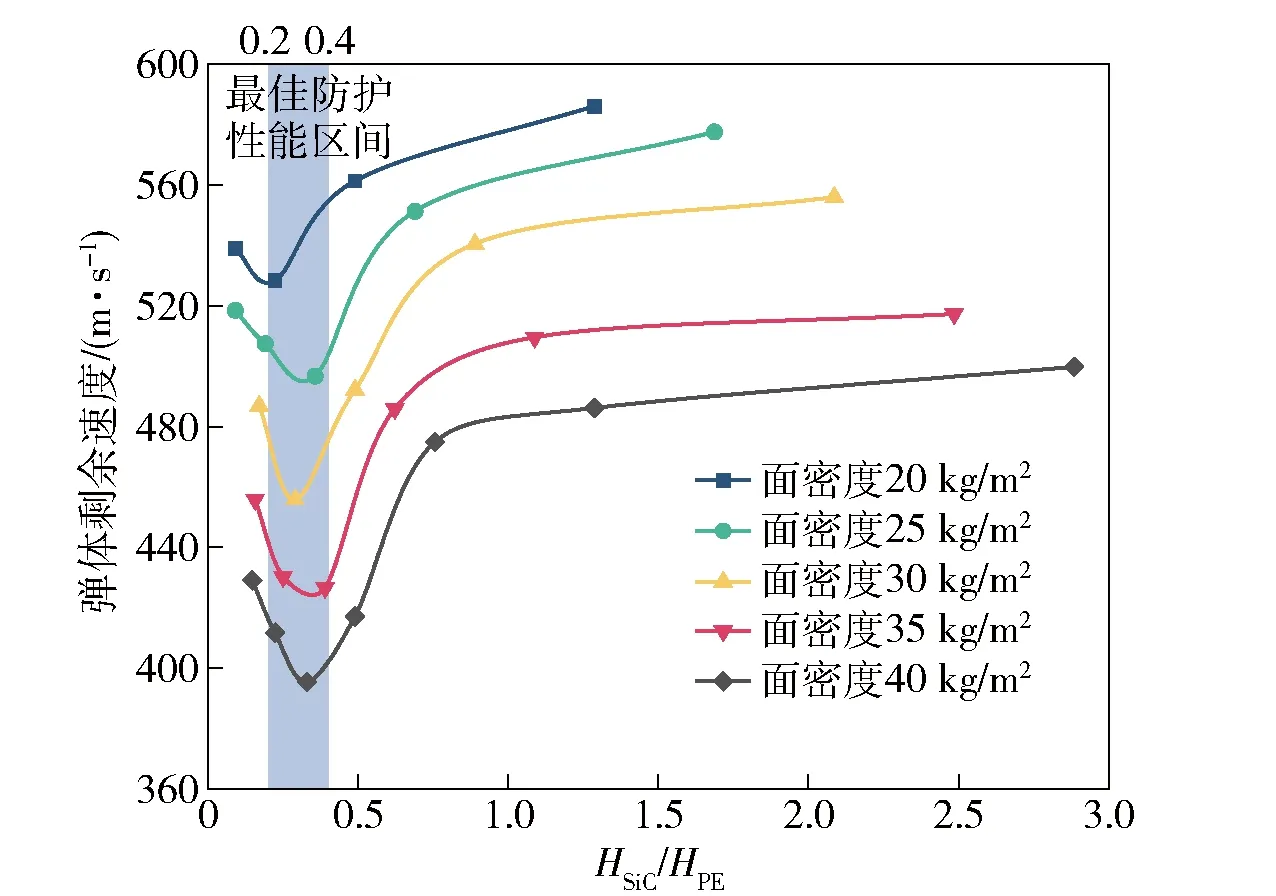
图14 弹体剩余速度与复合结构组元厚度比关系Fig.14 Relationship between the residual velocity of projectile and the thickness ratio of composite structure component
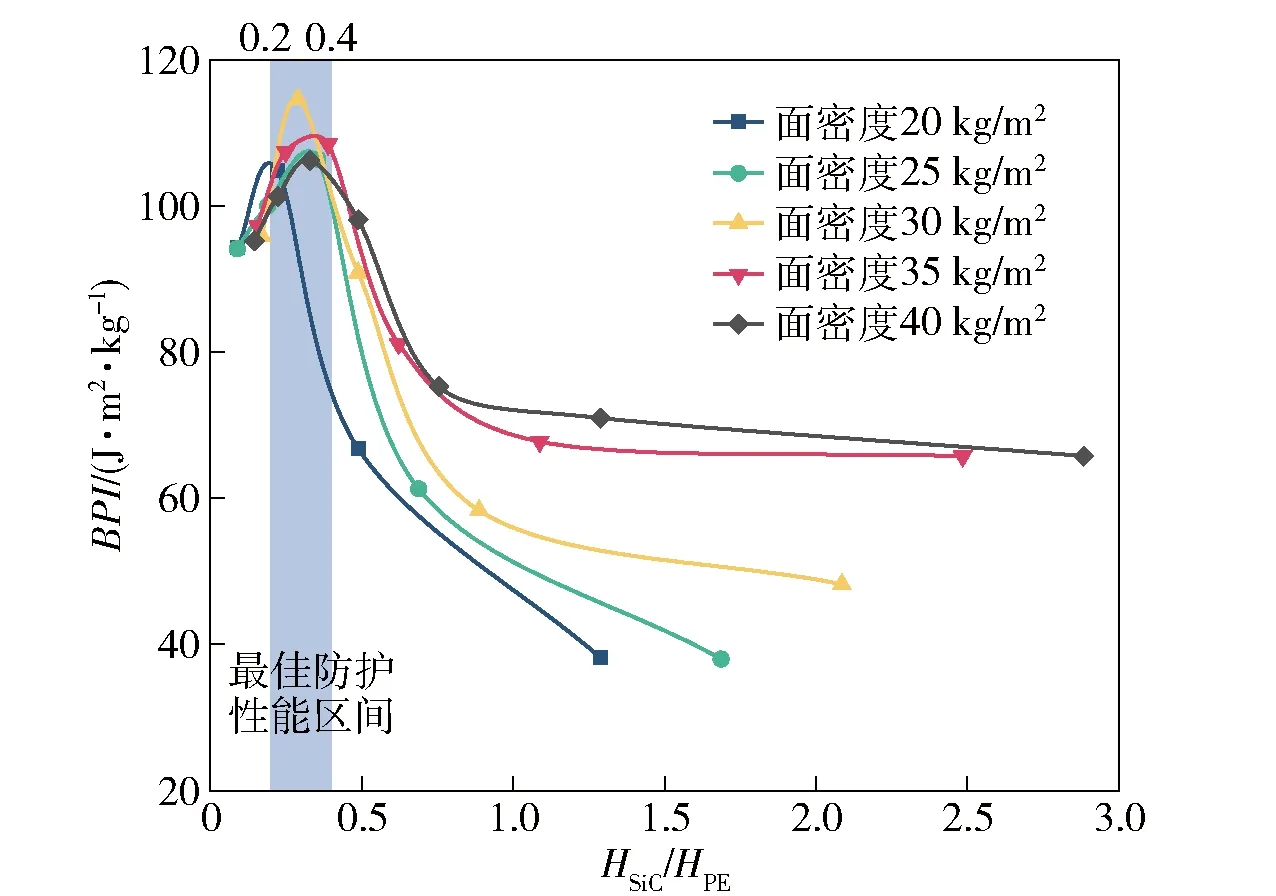
图15 复合结构单位面密度吸能与组元厚度比关系Fig.15 Relationship between energy absorption per unit area density and component thickness ratio of composite structure
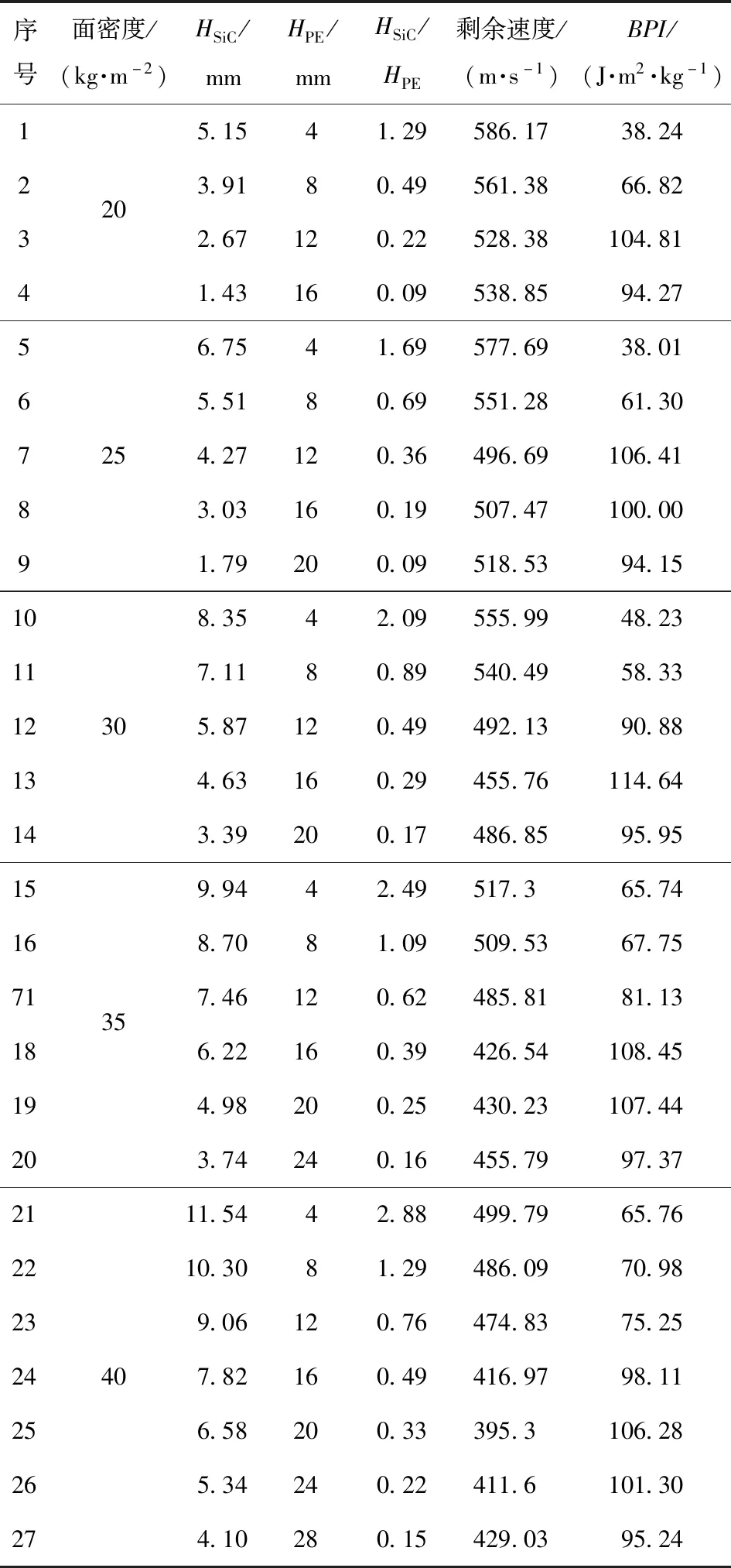
表7 弹体对不同组元厚度比复合结构侵彻的仿真计算结果Tab.7 Simulaed results of projectile penetrating into composite structures with different component thickness ratios
4 结论
本文采用弹道枪加载12.7 mm穿甲燃烧弹对SiC陶瓷板、UHMWPE纤维板层合而成的复合结构进行了弹体侵彻试验,采用被验证的有限元计算模型对12.7 mm穿甲燃烧弹侵彻不同厚度组元的复合结构进行了仿真计算,基于试验和仿真结果,分析了复合结构抗侵彻破坏机理。得到以下主要结论:
1) 本文所建立的有限元模型能够可靠计算12.7 mm穿甲燃烧弹对SiC陶瓷/UHMWPE复合结构的侵彻效应,计算结果与试验误差不大于5.71%。
2) 复合结构的抗弹性能分别随SiC陶瓷板和UHMWPE纤维板厚度的增加呈线性增加,SiC陶瓷板对抗弹性能的影响较UHMWPE纤维板大。
3) 当复合结构面密度在20~40 kg/m区间、SiC陶瓷板与UHMWPE纤维板厚度比小于3.0时,随组元厚度比的增加,复合结构抗弹体侵彻性能先增强后减小,当厚度比在0.2~0.4之间时,复合结构的抗弹体侵彻性能最佳。
