2，4-二硝基苯甲醚基熔铸含铝炸药冲击起爆特性

李淑睿，段卓平，白志玲，张旭，黄风雷

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081；2.中国工程物理研究院 流体物理研究所，四川 绵阳 621999)

0 引言

随着现代军事作战平台的发展，武器弹药的安全性决定了高价值作战平台的生存力和战斗力。钝感高能炸药是不敏感弹药装药发展的物质基础，例如2，4-二硝基苯甲醚(DNAN)基熔铸含铝炸药，具有能量密度高、感度低、易于装填等特点，是近年来不敏感弹药装药发展的重要方向，研究其冲击起爆特性和机理是了解其起爆特性和安全性能的关键，是弹药安全性设计和评估的基础和前提。

通过冲击起爆一维拉格朗日分析实验，获得冲击起爆爆轰成长过程反应流场的详细信息，如不同拉格朗日位置的压力、粒子速度变化历史，是确定冲击起爆机理和反应流模型参数的重要依据。随着测试技术的发展，包括嵌入式锰铜压阻压力传感器、组合式电磁粒子速度计和光子多普勒测速技术等在非均质固体炸药冲击起爆一维拉格朗日实验测试系统中得到了广泛应用，其中采用组合式电磁粒子速度计测速技术，只需1发实验就可获得更多拉格朗日位置的流场参数变化历史曲线。

本文采用火炮驱动蓝宝石飞片，实现平面冲击加载技术和组合式电磁粒子速度计测速技术，建立DNAN基熔铸含铝炸药RD-1X(60% HMX，30% DNAN，10%铝粉)一维冲击起爆实验及测试系统，测量不同飞片速度下不同固相炸药颗粒度RD-1X炸药冲击起爆爆轰成长过程的粒子速度变化历史，并确定RD-1X炸药的冲击Hugoniot关系及其未反应炸药JWL状态方程参数。

1 实验设计

建立飞片平面冲击加载炸药起爆一维拉格朗日电磁粒子速度测速实验系统，如图1所示，利用火炮加载系统，驱动蓝宝石飞片高速撞击RD-1X炸药样品，实现一维平面冲击加载，设置光子多普勒测速(PDV)探头测量飞片的撞击速度，利用组合式电磁粒子速度计测量冲击起爆爆轰成长反应流场的粒子速度。实验用蓝宝石飞片直径为55 mm，厚度12 mm。被测RD-1X炸药样品由两个角度为30°的楔形药块组成，组合后圆柱形药柱尺寸为42 mm×30 mm。图1中，为均匀磁场的强度。

图1 飞片平面冲击加载炸药起爆一维拉格朗日电磁粒子速度计测速实验系统Fig.1 One-dimensional Lagrange-velocity measuring system with a multiple electromagnetic particle velocity gauge for flyer impact initiation

实验所用组合式电磁粒子速度计由8个电磁粒子速度计组成，相邻粒子速度计所测深度间隔为1 mm，因此1发实验即可测得RD-1X炸药内部8个不同拉格朗日位置的粒子速度变化历史。实验时，利用环氧树脂将组合式电磁粒子速度计粘贴于两个楔形炸药块之间，并整体置于均匀磁场内部，炸药粒子在冲击波作用下发生运动，电磁粒子速度计敏感单元会跟随当地粒子一起运动，从而切割磁感线产生感应电动势。利用示波器记录电磁粒子速度计产生的电动势，根据电磁感应定律可获得相应位置的粒子速度为

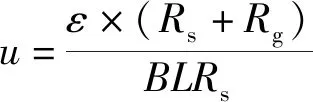
(1)

式中：为示波器和测试电路的总电阻；为电磁粒子速度计的电阻；为电磁粒子速度计测量段的长度。

RD-1X炸药的组分配比与爆轰性能参数如表1所示。为探索固相炸药颗粒度对RD-1X熔铸含铝炸药冲击起爆爆轰成长过程的影响，本文采用颗粒级配技术，将≤45 μm、125～180 μm和250～425 μm 3种不同粒径范围的奥克托今(HMX)炸药样品按照表2所示的比例进行混合，制备细颗粒、中等颗粒和粗颗粒3种颗粒度的RD-1X炸药样品，其中所添加铝粉的平均粒径约为10 μm。

表1 RD-1X炸药的组分和爆轰性能参数Tab.1 Component and detonation properties of RD-1X

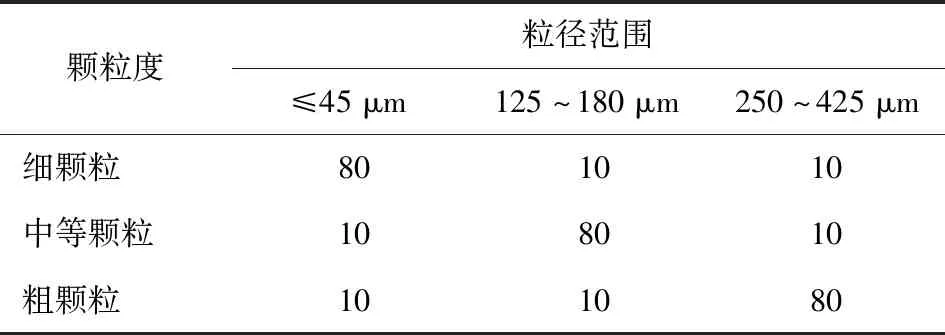
表2 RD-1X炸药中HMX颗粒度及级配比例Tab.2 Particle size and mixture ratio of HMX in RD-1X %

2 实验结果与分析

本文共进行4发RD-1X炸药冲击起爆电磁粒子速度测速实验，分别测得不同飞片撞击速度和不同颗粒度下RD-1X含铝炸药冲击起爆过程中1～8 mm拉格朗日位置处的粒子速度变化历史，实验结果如图2所示。图2中，横坐标为相对时间，均以1 mm位置处的冲击波到达时间为时间零点。在第2发实验过程中，由于示波器单个通道出现故障，未获得6 mm位置处的粒子速度变化曲线。

图2结果显示，在RD-1X炸药前期冲击起爆过程中，炸药内部各拉格朗日位置冲击波阵面附近的炸药粒子速度均较低，随着波后化学反应的进行，炸药粒子速度逐渐增大，波后粒子速度曲线出现明显的上升过程，曲线整体呈现驼峰形状，表明炸药点火后燃烧反应速率较快，燃烧反应阶段贡献较大。随着拉格朗日位置的深入，粒子速度波峰向前追赶前导冲击波阵面，这是因为相对冲击波，反应流动是超声速的。峰值后粒子速度下降是因为随着化学反应的进行，下游反应区压力增加阻止了粒子向前运动。此外，飞片速度越大或炸药颗粒度越小，波后炸药粒子速度的增长速率越快，粒子速度曲线上升段的斜率越大，表明炸药颗粒度越小，炸药点火后燃烧反应速率越快。

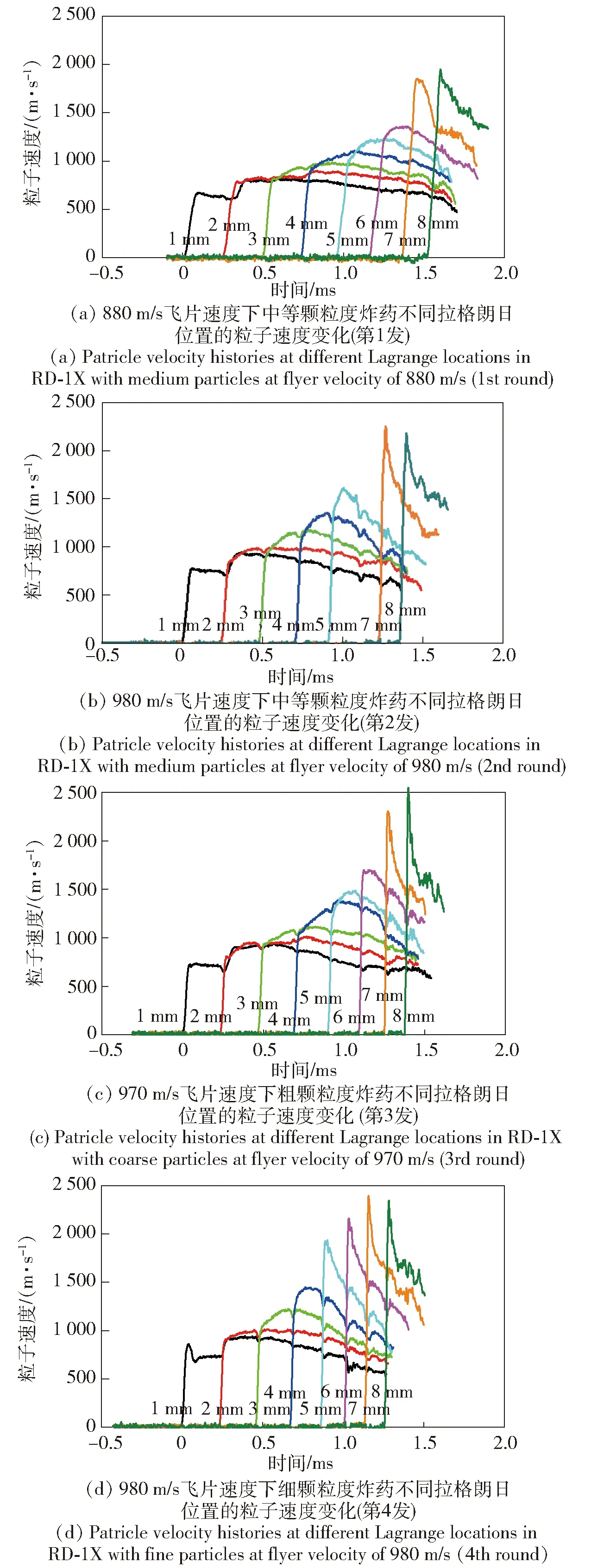
图2 RD-1X炸药冲击起爆爆轰成长过程的粒子速度- 时间实验曲线Fig.2 Experimentally measured particle velocity-time profiles for the shock initiation and detonation growth processes of RD-1X

值得指出的是，实验测得的炸药粒子速度- 时间曲线上均能观察到多次、微小的扰动，且扰动出现的时间均与其后续拉格朗日位置的冲击波到达时间相吻合，这是因为冲击波到达后续拉格朗日位置的粒子速度计时，速度突变使感应电动势突变，引起测量磁场扰动，从而对其炸药粒子速度变化曲线产生干扰，这是组合式电磁粒子速度计测量结果的典型特征。此外，如图2(d)所示，第4发实验中1 mm位置处紧随前导冲击波阵面后出现粒子速度异常抖动现象，分析原因可能是该发实验在安装过程中电磁粒子速度计与楔形炸药样品未紧密贴合即存在空气间隙导致的。

提取不同飞片撞击速度下中等颗粒度RD-1X炸药冲击波时程曲线，如图3(a)所示，飞片撞击速度越高，加载压力越高，RD-1X炸药内同一拉格朗日位置的冲击波到达时间越早，炸药内部的冲击波传播速度越快。进一步结合图2(a)和图2(b)所示的粒子速度变化曲线分析，加载压力越高，前导冲击波阵面粒子速度增长越明显，波后粒子速度成长速率越快，粒子速度高峰不断追赶前导冲击波阵面而越早转为爆轰。

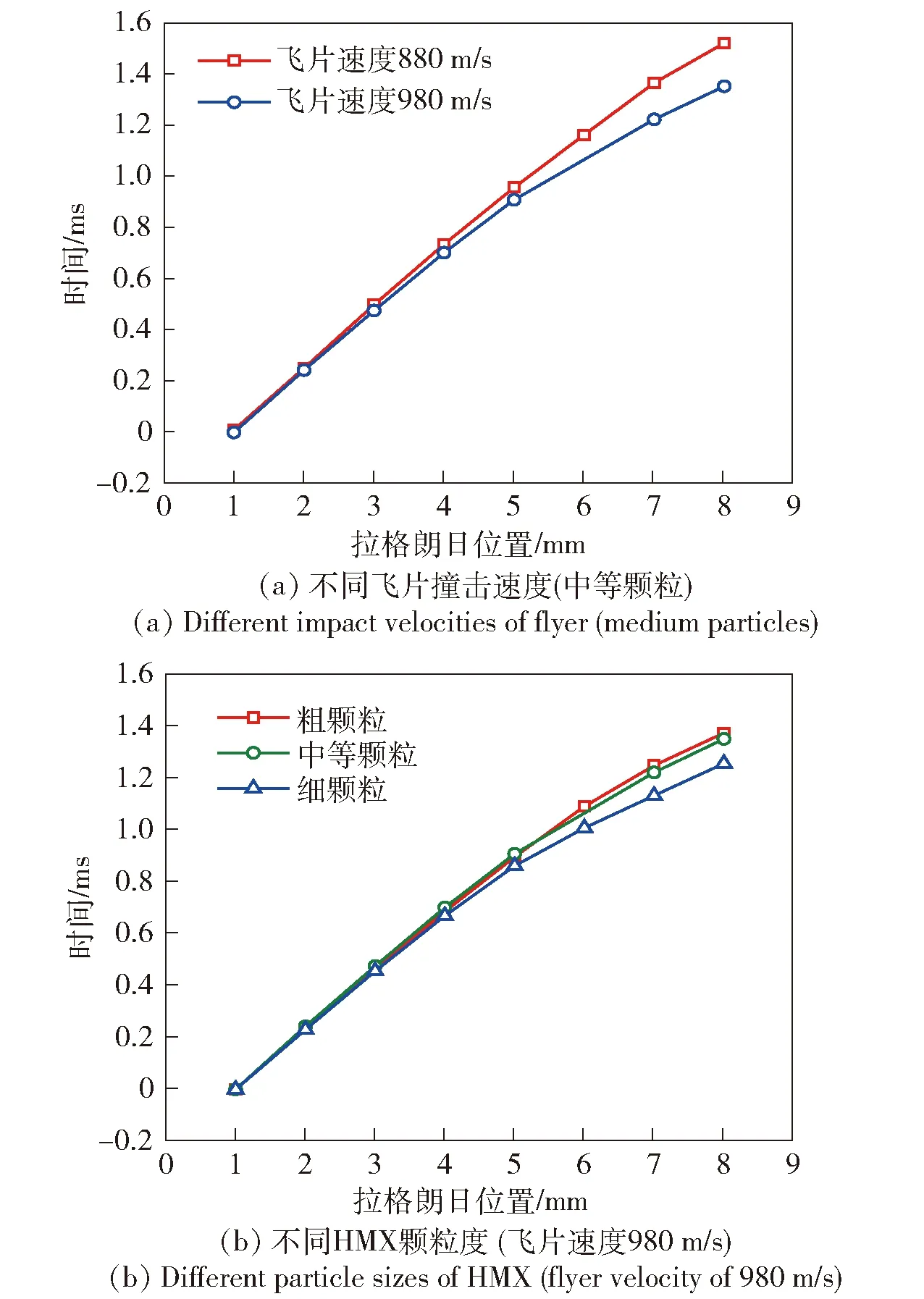
图3 RD-1X炸药冲击波时程曲线的对比Fig.3 Comparison of leading wave trajectories in RD-1X

在冲击载荷作用下，炸药反应热点的临界直径和临界点火温度满足如下关系式：

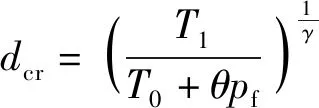
(2)

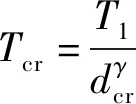
(3)

式中：为炸药初始温度；、和为炸药常数。由(2)式、(3)式可见，载荷越大，反应热点的临界直径越小，临界点火温度越高，因此炸药内部能发生反应的热点数量越多，热点点火反应越快且燃烧反应(爆轰成长)也越快，到爆轰时间越早，到爆轰距离越短。

同一飞片撞击速度下3种颗粒度RD-1X炸药冲击波时程曲线如图3(b)所示，可见细颗粒炸药冲击起爆反应最快，最早转为爆轰，中等颗粒次之，粗颗粒最慢。同样结合图2(b)～图2(d)粒子速度变化分析可知，颗粒度越细，前导冲击波阵面粒子速度增长越快，波后粒子速度成长速率越快，粒子速度高峰追赶前导冲击波阵面现象越明显，最早形成爆轰。分析原因，是因为在本文装药颗粒度级配范围和加载压力下，细颗粒炸药激活的反应热点数量最多，热点点火反应速率最快，快速释放的能量直接推动了波阵面粒子速度升高；同时细颗粒炸药燃烧比表面积最大，燃烧反应贡献最大，波后粒子速度成长速率最快。此外，同一拉格朗日位置的粒子速度峰值后细颗粒炸药粒子速度下降速率最快，是因为其下游反应区压力成长最快，阻止炸药粒子向前运动，细颗粒炸药冲击起爆爆轰成长过程整体呈现加速反应特征。

3 未反应炸药状态方程参数确定

假设前导冲击波阵面上炸药不发生化学反应，读取图2中RD-1X炸药冲击起爆实验各拉格朗日位置的粒子速度历史前沿数据，可得未反应RD-1X炸药的波后粒子速度数据。采用插值方法修正实验数据中冲击波阵面上升沿对炸药粒子速度判读的影响，获得图2中每发实验各拉格朗日位置(=1，2，…，8)的冲击波阵面到达时间和波阵面上的炸药粒子速度数据p，如表3所示。

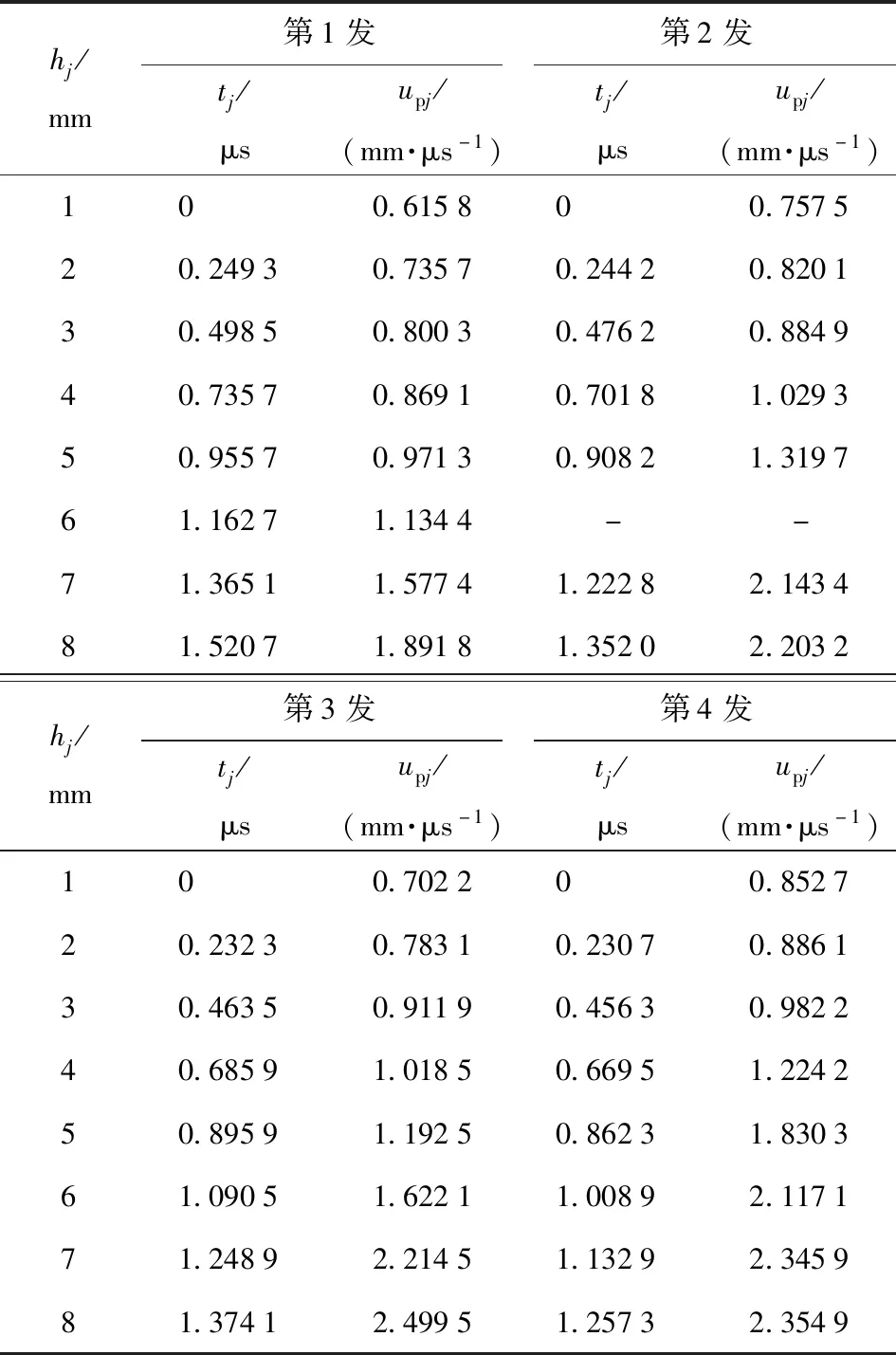
表3 RD-1X炸药冲击起爆实验各拉格朗日位置冲击波阵面到达时间和波阵面上的粒子速度Tab.3 Arrival time of shockwavefront and particle velocity at each Lagrange location in shock initiation tests of RD-1X

本文采用拟合求导方法，利用各拉格朗日位置处冲击波到达时间确定冲击波的传播速度。由于表3所示冲击波到达时间均为相对时间，则拟合冲击波时程曲线时需采用相对位置′，即各位置与1 mm拉格朗日位置之间的相对距离。采用4次多项式对4发冲击起爆实验的′-数据进行拟合，可得冲击波阵面时程曲线为

′()=+++

(4)

式中：′为冲击波达到位置(mm)；为冲击波达到时间(μs)；、、、分别为常数系数。

对(4)式进行求导，可得冲击波传播速度随时间的变化关系式，将表3中的冲击波到达时间代入，即可得到各拉格朗日位置的冲击波传播速度。至此，本文根据4发RD-1X炸药冲击起爆实验数据，获得4组未反应RD-1X炸药的-p数据，对其进行线性拟合，拟合结果如图4所示，则得RD-1X炸药的冲击Hugoniot关系为

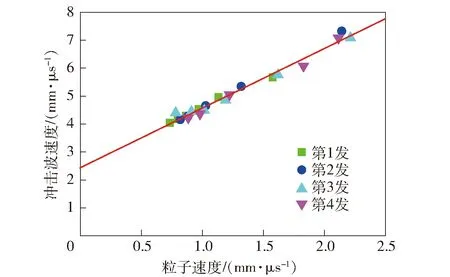
图4 RD-1X炸药的冲击Hugoniot关系Fig.4 Shock Hugoniot relation of RD-1X

=(2439±0087 7)+(2137±0066 7)

(5)

式中：0735 7 mm/μs≤≤2214 5 mm/μs。将(5)式外推到RD-1X炸药的爆速，可得炸药冯·诺依曼峰值压力=3906 GPa，压力比值=1395，为爆压。

带化学反应的流场计算时，爆轰反应与混合物组分的温度密切相关，反应材料模型中未反应炸药状态方程通常采用如下含温度形式的JWL状态方程：

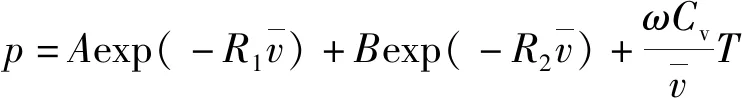
(6)

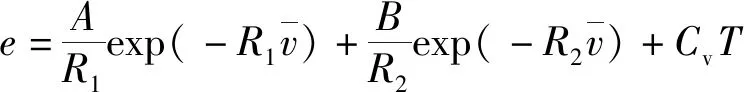
(7)

exp(-)+exp(-)+298=0

(8)

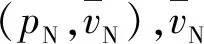
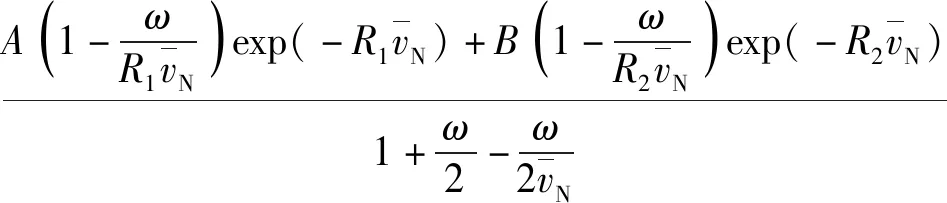
(9)

根据冲击波阵面守恒关系式，有

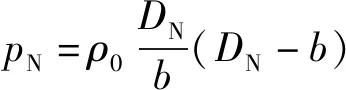
(10)

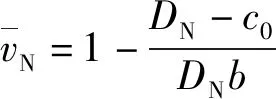
(11)

式中：为炸药爆速；为初始密度；、为炸药冲击Hugoniot参数，=2439 mm/μs，=2137。

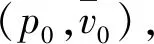
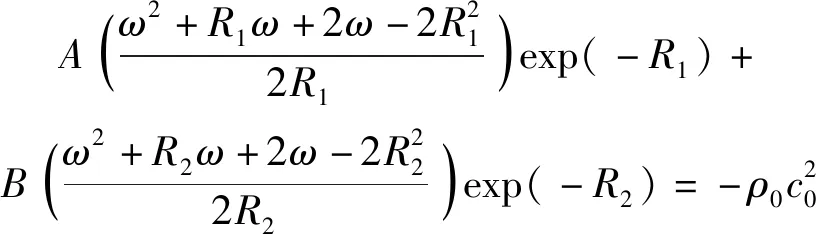
(12)

式中：为炸药冲击Hugoniot压力。

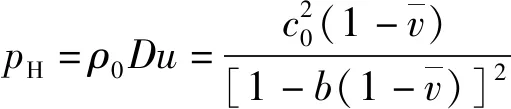
(13)

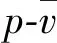
表4 RD-1X炸药的未反应炸药JWL状态方程参数Tab.4 Parameters of JWL EOS for unreacted RD-1X

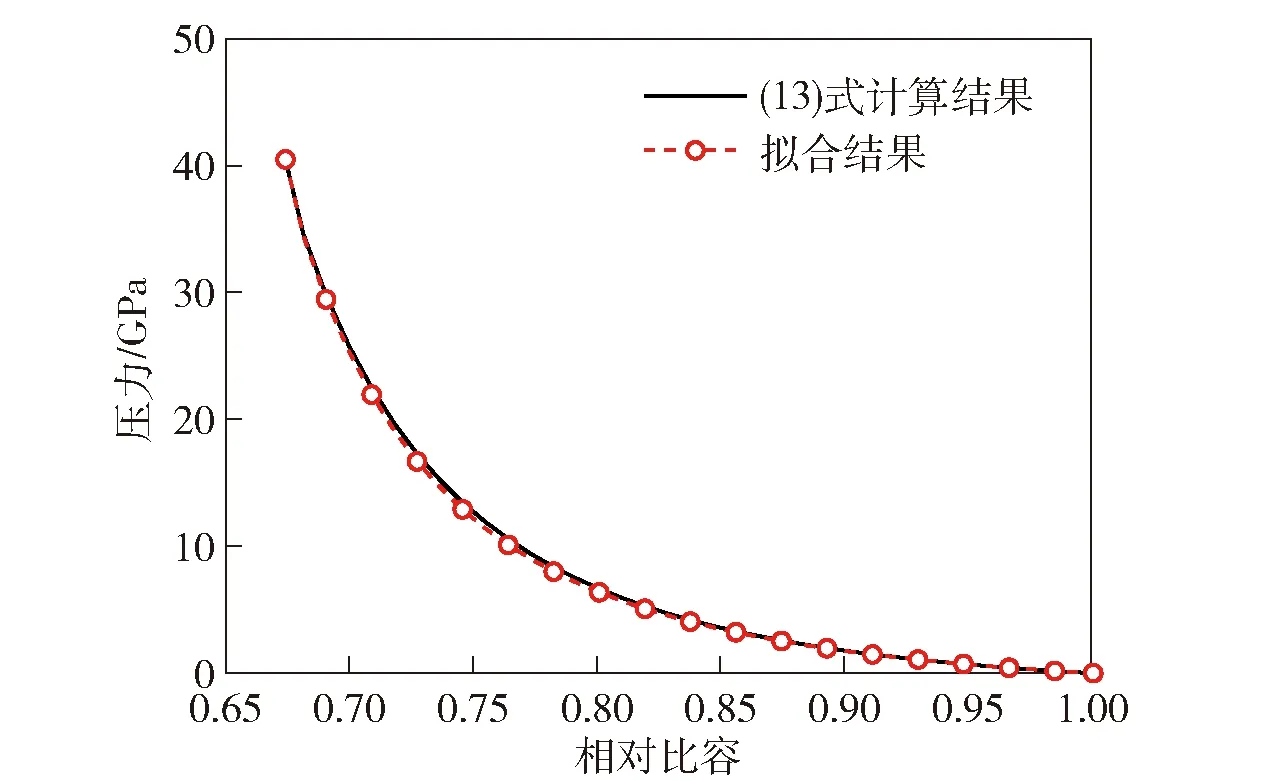
图5 RD-1X炸药冲击Hugoniot曲线的拟合结果Fig.5 Fitting result of shock Hugoniot curve of RD-1X

4 结论

本文开展了DNAN基熔铸含铝炸药RD-1X的冲击起爆实验，研究了加载压力和HMX颗粒度变化对RD-1X炸药冲击起爆爆轰成长过程的影响规律。利用各拉格朗日位置的粒子速度历史前沿数据和冲击波时程曲线，确定了RD-1X炸药的冲击Hugoniot关系和未反应炸药JWL状态方程参数，为建立冲击起爆反应速率模型和验证模型适应性提供了数据基础。得出主要结论如下：

1) RD-1X炸药冲击起爆过程中，波后炸药粒子速度上升明显，粒子速度曲线整体呈驼峰状，表明RD-1X炸药热点点火后燃烧反应速率较快，燃烧反应贡献显著，促使粒子速度峰值加速追赶前导冲击波阵面，其冲击起爆爆轰成长过程整体呈现加速反应特征。

2) RD-1X炸药冲击起爆爆轰成长过程主要受热点点火和燃烧反应过程共同控制。在本文装药颗粒度级配范围和加载压力下，加载压力越高或炸药颗粒度越细，冲击起爆过程中反应热点数量越多，点火反应速率越快，快速释放的能量直接推动前导冲击波阵面粒子速度增长；炸药颗粒度越细，燃烧比表面积越大，燃烧反应贡献越大，促使波后粒子速度增长明显，熔铸含铝炸药细观结构对其冲击起爆过程具有显著影响。

3) 利用炸药冲击起爆实验测得的冲击波阵面前沿数据确定炸药的冲击Hugoniot关系，将其外推至爆速时所得冯诺依曼峰值压力在合理范围内；在满足3个相容关系前提下确定的RD-1X未反应炸药JWL状态方程参数为冲击起爆反应速率模型参数研究奠定了基础。