基于近似模型的复合材料导管支臂结构性能分析

2022-07-05李彬谢新唐文勇陶江平孙宜强张辉

兵工学报 2022年6期

李彬，谢新，唐文勇，陶江平，孙宜强，张辉

(1.上海交通大学船舶海洋与建筑工程学院，上海 200240；2.上海船舶工艺研究所，上海 200032)

0 引言

气垫船推进器导管具有导流与保护作用，是系统中重要的特种装备结构[1]。随着气垫船逐渐向大型化发展，导管整体结构性能要求越来越高。支臂作为导管的主要支撑连接结构，在导流、支撑以及减重等方面发挥着重要作用，其结构性能需求变得愈加苛刻。复合材料作为新型材料的代表，具有比强度大、比刚度高、耐腐蚀性好等多个性能特点。相比传统金属结构，在等强度、刚度条件下，质量大幅减轻，对导管和气垫船结构轻量化设计具有重要意义。目前关于导管复合材料支臂的研究成果较少，且在材料参数对支臂结构性能的影响方面分析尚不充分，此外复合材料结构性能数值分析又具有计算量大、耗时较长的缺点。

可设计性是复合材料最突出的优点，对复合材料支臂进行结构设计时需要全面分析材料、配比、铺层、布局以及工艺等对结构性能的影响，以满足特殊工程背景的应用需求。复合材料宏观力学性能没有考虑材料刚度随组分含量变化的情况，因此需要结合细观力学理论来确定如何通过改变组分含量以获得预期刚度。通过细观力学方法预测复合材料结构的性能参数，这些参数可用于结构宏观力学分析。从材料设计角度看，细观力学是宏观力学分析的得力助手。由于复合材料结构设计中的材料种类、铺层方式、结构特点以及加工工艺等方面具有诸多备选方案，直接采用试验研究方法进行设计的成本较高。科研及工程领域通常采用数值模拟与试验研究互相补充的分析方式进行设计，这样既能全面分析结构力学性能，还可以提高结构设计的效率和经济性[2]。杨卓懿[3]利用有限元方法对复合材料潜水器结构响应规律进行分析，验证了复合材料结构有限元分析的准确性。程妍雪等[4]、李彬等[5]进行了基于神经网络的水下航行器均匀环肋耐压壳结构研究。赵群等[6]利用近似模型对复合材料壁板强度进行了研究。以上部分研究采用了近似模型的方法研究复合材料结构力学特性，然而针对铺层角影响计算模型精度的问题，有待深入分析。

本文采用试验设计方法生成样本空间，通过统计学手段研究材料参数对复合材料导管支臂结构性能的影响。在材料力学理论的复合材料结构刚度分析基础上，结合有限元分析方法，利用神经网络构建近似模型。由于复合材料层合板结构性能对铺层角变化敏感，当将全部铺层角度作为输入变量且变化范围较大时，构建单一近似模型精度受到影响。为此本文提出一种带有动态权重系数的组合神经网络近似模型方法，用以提高铺层角作为设计变量时近似模型的精度。根据结构综合性能指数对各铺层结构性能影响的灵敏度进行分析并分组后，建立多个神经网络模型，结合权重系数与各模型输出得到响应预测值。采用近似模型对复合材料导管支臂结构性能参数进行分析，从细观与宏观两方面研究材料参数对支臂性能的影响规律，为后续复合材料导管设计提供参考。

1 复合材料导管支臂结构有限元分析

1.1 复合材料导管支臂结构概述

气垫船推进器位于导管内部，其支臂作为主要支撑结构连接了导管筒体内部与推进器导流罩，如图1所示。其中，支臂为翼型结构，由蒙皮和筋板构成，筋板在支臂内部均匀布置。图1同时展示了本文涉及的坐标系，研究采用笛卡尔坐标系，x轴为纵向船长方向，y轴为横向船宽方向，z轴为竖直方向。

图1 气垫船推进器导管支臂结构示意图Fig.1 Duct supporting structure for hovercraft thruster

1.2 单层板力学性能参数

为确定单层复合材料整体力学性能，对复合材料支臂结构刚度进行细观层面的研究，采用材料力学分析方法结合纤维体积分数进行计算[7]，并采用以下假设：1)单层板是线弹性的，宏观均匀且正交各向异性，无初应力；2)纤维和基体都是线弹性的，均匀且各向同性；3)纤维排列规则，与基体理想粘结。

在单向纤维复合材料中，假设纤维和基体在纤维方向应变相等，纤维体积分数改变时的单层板弹性常数通过材料力学理论进行计算求解。设E1为纤维方向弹性模量，E2为纤维横向弹性模量，

E1=EfVf+EmVm=EfVf+Em(1-Vf)

(1)

(2)

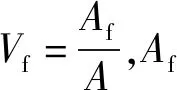
设ν12为轴向泊松比，它是当σ=σ1，σ2、σ3均为0时，横向应变ε1与纵向应变的ε2负比值，由(3)式表示为

ν12=νmVm+νfVf=νm(1-Vf)+νfVf

(3)

式中：νf、νm分别表示纤维、基体泊松比。

剪切模量由(4)式表示为

(4)

式中：Gf、Gm表示纤维、基体剪切模量。

1.3 失效准则

复合材料具有各向异性的特点，其应力最大值与结构最危险状态不具有绝对联系。复合材料失效准则与金属材料不同，因此无法简单应用金属材料设计规范中的准则来校核复合材料构件失效情况。本文采用Tsai-Wu强度理论[8-11]来判定复合材料导管支臂是否失效。作为一种常用的复合材料失效理论，Tsai-Wu准则不但考虑了应力分项间的耦合作用，而且区分了拉伸强度和压缩强度。在平面应力下的正交各向异性复合材料失效面由(5)式进行表示，当失效面公式值小于1时认为结构满足强度要求，否则认为结构失效：

(5)

式中：σ1和σ2分别表示材料纵、横向应力分量；σ6为主方向剪切应力；F1、F2、F11、F12、F22和F66为强度张量系数，

(6)

Xt、Xc分别表示纵向拉伸、压缩强度，Yt、Yc分别表示横向拉伸、压缩强度，S表示剪切强度。

除此之外，参考国家标准GB/T 25383—2010风力发电机组风轮叶片中规定，要求碳纤维材质结构轴向拉伸、压缩应变小于许用应变0.25%，剪切应变小于许用应变0.45%。

1.4 支臂结构有限元分析

复合材料导管支臂结构采用碳纤维/环氧树脂复合材料。复合材料层合板单层厚度为0.35 mm，铺层角[0°，45°，-45°，45°，-45°，45°，-45°，90°]s(s表示对称铺设)，采用16层对称铺设方式。材料性能参数[12]如表1所示。层合板中纤维和基体的体积分数影响各层的力学性能，进而对整体结构响应规律造成影响。

表1 材料力学性能参数Tab.1 Mechanical properties of materials

采用Shell单元对导管支臂结构进行离散，支臂一端刚性固定，另一端施加导管筒体受外载荷作用所产生的截面力，通过面载荷施加在端部。有限元模型及铺层角示意图如图2所示。设支臂载荷为x轴方向17 000 N，对有限元模型进行求解，得到导管支臂的轴向应变、径向应变、剪切应变以及基于Tsai-Wu失效准则的失效因子。有限元计算结果如图3所示。

图2 支臂有限元模型与铺层角示意图Fig.2 FEM model of the supporting structure and ply angles

图3 导管支臂结构计算结果Fig.3 Contour plots of supporting structure

2 导管支臂结构神经网络近似模型

2.1 径向基函数神经网络近似模型

与传统金属材料相比，复合材料因各向异性、多元化、离散化等特性，增加了结构设计难度与计算量。对设计方案逐一进行有限元分析将导致计算成本增加，使设计效率降低。为了平衡计算精度与速度，根据适当数量样本的输入输出建立待分析问题的近似模型，能够代替大量重复的有限元分析，且可为优化设计提供便利条件[13]。通常近似模型无需针对具体物理意义进行分析，只需根据样本点输入输出建立函数关系即可：

(7)

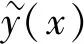
径向基函数(RBF)神经网络模型是一种前向型人工神经网络，具有良好的非线性逼近能力[14-16]。RBF神经网络由输入层、隐含层和输出层组成。对待测点到样本点求欧几里得距离，径向函数以这个距离作为自变量函数，将其当作基函数进行线性叠加即可形成RBF模型。输入信号在层间传递是一种映射过程，由输入层到隐含层再到输出层，将上级变量转换到新空间。其中输入层到隐含层为非线性映射，隐含层到输出层为线性映射。输入层到隐含层的映射关系与中心点有关，隐含层到输出层利用加权和函数，其中权值可以调整，权值求解过程可以由线性方程组计算得到。由此RBF神经网络的权值调整过程将易于计算更新，同时保证了全局极值，防止落入局部极值。最终由输入到输出经历非线性过程。构建RBF神经网络模型，设变量空间维度为n，神经元数为N，输入变量x由此进入网络，隐含层有P个神经元，第p(p≤P)个神经元的输入信息为hp=‖x-cp‖，输出信息为φ(hp)，输出层有1个神经元，则加权求和公式如下：

(8)

神经元作用规律是当x到基函数中心cp的任一坐标距离很小时产生响应输出。为了处理函数大范围的响应，RBF模型常利用高斯样条函数作为基函数进行线性叠加。高斯样条函数的形式为

(9)

式中：cpi(i=1,2,…,n)为第p个基函数的中心；σpi(i=1,2,…,n)为第p个基函数的方差。

通过试验设计的方法生成样本并采集数据以构建近似模型，为衡量其准确性需进行误差分析[17]。设Ns为样本点数，yη为输出变量真实值，η为近似模型估计值，为输出变量真实值的平均值。采用相对均方根误差(RRMSE)、相对平均值误差(RAAE)进行全局精度预测，误差值越小，说明近似模型的全局精度越高。

(10)

(11)

采用最大绝对误差(RMAE)进行局部精度预测，误差值越小说明局部预测精度越高。基于复相关系数R2预测拟合精度，R2取值越接近1，说明近似模型拟合精度越高。

(12)

(13)

2.2 组合神经网络近似模型方法

组合神经网络近似模型通过若干模型加权线性叠加组成。

(14)

式中：yEM(x)为组合神经网络近似模型的预测输出值；M为单一神经网络模型个数；wα为第α个近似模型的权重系数。为得到准确度更高的近似模型，权系数的选取是重要环节。通常，精度较高的模型对应的权系数较大，相对放大高精度模型的影响；精度较低的模型对应的权重系数较小，以相对削弱其影响。

组合近似模型的权重系数计算方法主要包括反比例平均法、启发式算法和交叉验证方法等。在解决工程实际问题中，为了平衡计算效率与计算精度，交叉验证方法更具优势[18]。通常利用求解优化问题的方法对权系数进行计算。其中设计变量为对应近似模型的权系数wα，目标函数为交叉验证均方差，即

(15)

式中：yact为实际响应值；xk为样本点，k为样本点序号。

2.3 复合材料导管支臂结构参数近似模型

为构建复合材料导管支臂结构近似模型，对支臂进行参数化建模并编写参数化设计语言APDL命令流，利用ANSYS软件进行有限元分析，并基于优化拉丁超立方试验设计安排样本点，根据输入输出变量训练RBF神经网络。输入变量为材料参数，包括基体弹性模量Em、基体剪切模量Gm、纤维弹性模量Ef、纤维剪切模量Gf、纤维体积分数Vf与铺层角θ1、θ2、θ3、θ4、θ5、θ6、θ7、θ8，参数范围如表2所示。导管支臂的结构响应作为输出变量，主要包括Tsai-Wu失效因子Fc、轴向应变ε和剪切应变γ。其中失效因子主要针对复合材料部分，而轴向和剪切应变针对整个支臂结构。

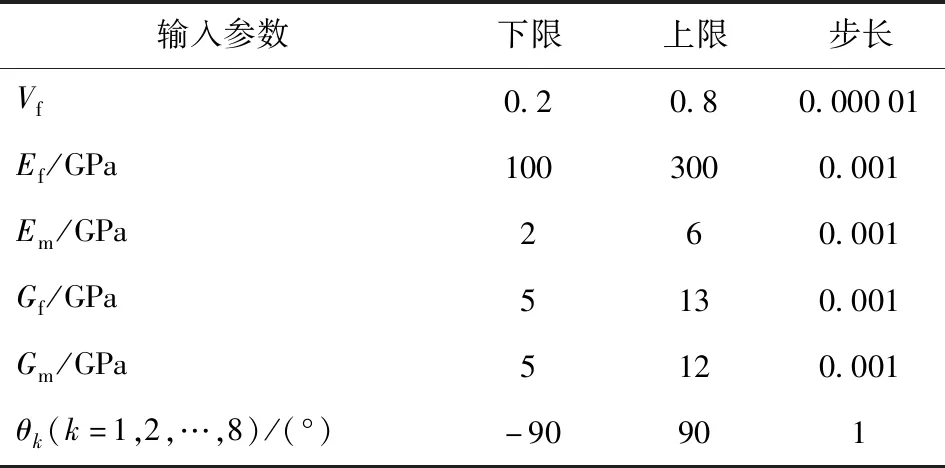
表2 输入参数范围Tab.2 Range of input parameters

导管支臂层合板铺层角度具有离散化、多值化以及范围大等特征，且支臂结构性能受铺层角变化影响规律复杂，直接将所有角度同时作为设计变量时，在有限的试验样本条件下，所构建的神经网络近似模型精度较低。为解决这一问题，本文采用组合神经网络近似模型方法。

以Tsai-Wu失效因子Fc为例，在样本点个数为400时，同时将全部铺层角作为设计变量，构建单一RBF近似模型，误差分析结果R2值为0.5。通常R2值达到0.9认为具有足够精度，可见同时将全部铺层角作为设计变量构建单一模型时，RBF近似模型准确度较低。对Fc进行主效应分析与灵敏度分析，可以得到各个铺层角θ1,θ2,…,θ8对Fc值的影响贡献度排序，本文算例失效因子Fc的Pareto图如图4所示。

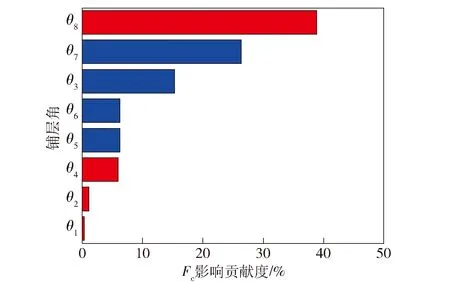
图4 失效因子Fc影响百分比Fig.4 Pareto chart of failure factor Fc

根据各铺层角的影响贡献度，对铺层角进行分组。此时需注意分组数量不宜过多，防止引起计算量的增加以及精度的下降。当铺层角数目为8时，选择2～4组进行分组。基于灵敏度与影响的正反相关性，得到若干分组方式。遍历各分组方式并进行精度检验，选取误差最小的组合近似模型作为分析模型。通过建立分组RBF神经网络近似模型，输出变量失效因子Fc的R2值提高到了0.92，满足了精度要求。针对其他输出变量，采用相同方法对铺层角进行重新分组，重新计算权系数并进行精度检验。综上，建立复合材料导管支臂组合RBF近似模型的流程如图5所示。

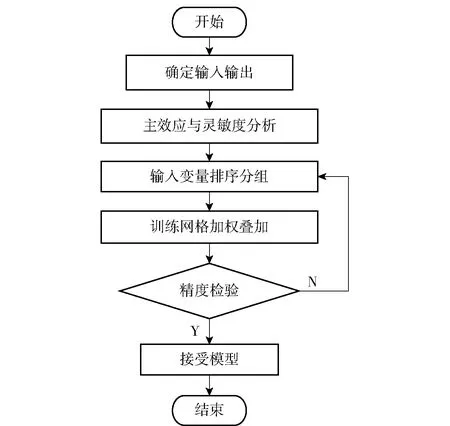
图5 组合RBF近似模型建立过程Fig.5 Establishing progress of ensemble RBF model

样本点数设置为400，基于优化拉丁超立方试验设计构建组合RBF近似模型，研究材料参数的影响，得到输入输出变量之间的非线性映射关系。图6 展示了复合材料导管支臂结构性能参数的部分近似模型三维图。

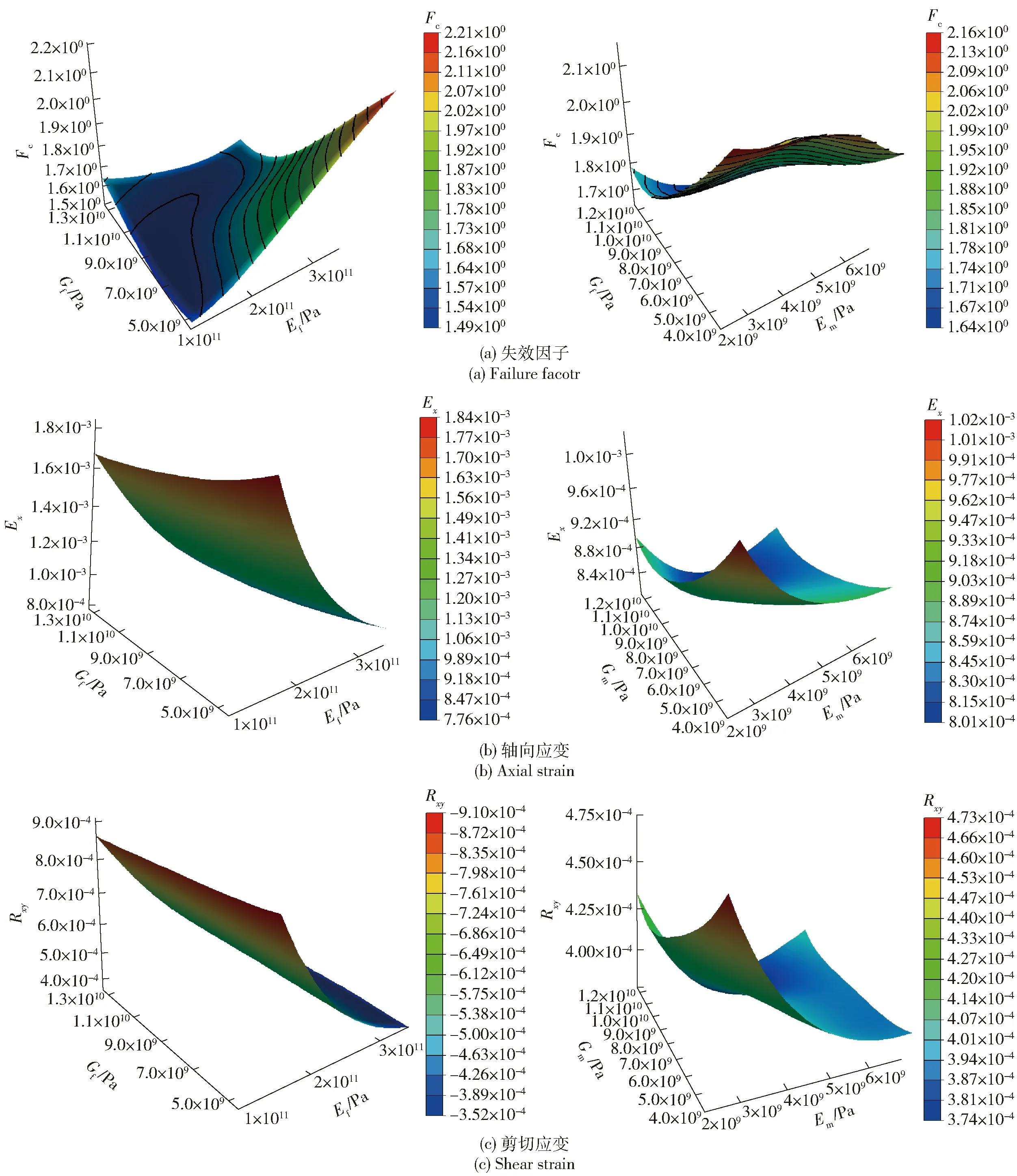
图6 弹性常数近似模型Fig.6 Approximation model of elastic constants

2.4 误差分析与计算性能

为了评估导管支臂组合RBF模型预测准确度，在设计空间内随机选取80个样本点，与有限元计算值进行对比。通过计算各误差指标可以看出复合材料导管支臂结构所有输出参数的R2值均大于0.9。误差指标计算结果如表3所示。其中，Ex、Ey、Ez分别为x、y、z3个方向正应变，Rxy、Ryz、Rxz分别为3个方向剪应变。近似模型预测值与有限元计算实际值对比如图7所示。图7中x轴为预测值，y轴为实际值，各点距离直线y=x越接近，表示预测精度越高。观察图7中轴向应变、剪切应变、失效因子的误差分析结果可知，该组合RBF近似模型具有良好的准确性。本文采用计算机硬件配置10核Core(TM) i9处理器，主频3.70 GHz，内存64 GB。开启多核并行计算的情况下，进行一次有限元分析平均耗时 35 s，然而利用近似模型进行一次计算平均仅需0.012 s。因此，结合试验设计方法构建复合材料导管支臂性能参数的组合RBF神经网络近似模型，可以在有限样本点数量下具有较小的误差。另外，在保证较高准确度的同时，以该模型代替有限元分析，能够大幅度降低计算时间，提高设计分析效率。

图7 近似模型误差分析Fig.7 Error analysis of approximate model

表3 近似模型误差分析Tab.3 Error analysis of approximate model

3 基于近似模型的复合材料导管支臂结构性能研究

为分析导管支臂结构性能的影响因素以及变化趋势，对导管支臂端部载荷设置纵向、横向、垂向3个方向，以及低、中、高3个载荷水平。工况组合如表4所示。基于2.3节导管支臂结构组合RBF神经网络近似模型，采用优化拉丁超立方试验设计对每个载荷工况设置1 000个样本点，利用近似模型代替有限元分析，得到各输出结果，并使用统计学工具对样本输入输出值的关系进行分析。本文利用近似模型方法分别从细观与宏观不同角度对材料参数的影响进行研究，包括以下方面：1)组分材料力学性能参数的影响；2)纤维体积分数的影响；3)纤维铺设角度的影响。

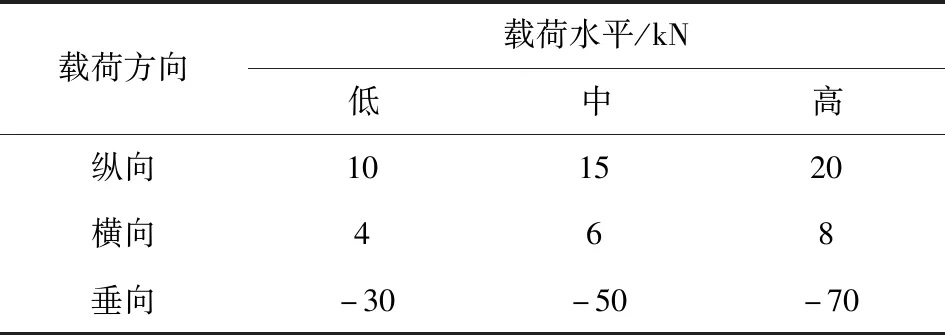
表4 工况组合Tab.4 Load case combination

3.1 组分材料工程弹性常数对支臂力学性能影响

根据2.3节样本点输入输出变量，对导管支臂结构响应进行敏感度分析，并用Pareto图表示。支臂端部各个受力方向以及载荷水平下的敏感度分析结果如图8所示。图8中百分比值越高，表明该输入变量对目标输出变量的影响程度越高。

图8 组分材料属性影响百分比Fig.8 Percentage effect of component material properties

根据统计分析结果可以发现，支臂材料工程常数中，纤维弹性模量的作用最为突出，在各向受力状态下其对材料结构响应均有较大作用。基体的剪切模量、基体弹性模量与纤维剪切模量也具有一定影响，然而其影响程度相比纤维弹性模量要低很多。支臂端部受力不同时，基体剪切模量对失效指数具有较为明显的影响。这是因为当载荷并非沿着纤维铺设方向时，基体的性能就会影响结构强度。通过垂向受力时的稳定性分析，发现纤维弹性模量对临界失稳压力影响最大。

纤维弹性模量对几种受力模式下的导管支臂强度和稳定性影响都很大。基体剪切模量的作用次之。通过研究各单独组分材料属性对导管支臂力学性能的影响，不但可以对支臂力学性能优化的方向进行预测，还可以在制备复合材料时对碳纤维及环氧树脂进行选型。

3.2 纤维体积分数对支臂力学性能影响

材料选定情况下，复合材料导管支臂力学性能随纤维体积分数变化的情况如图9所示。由图9可知：

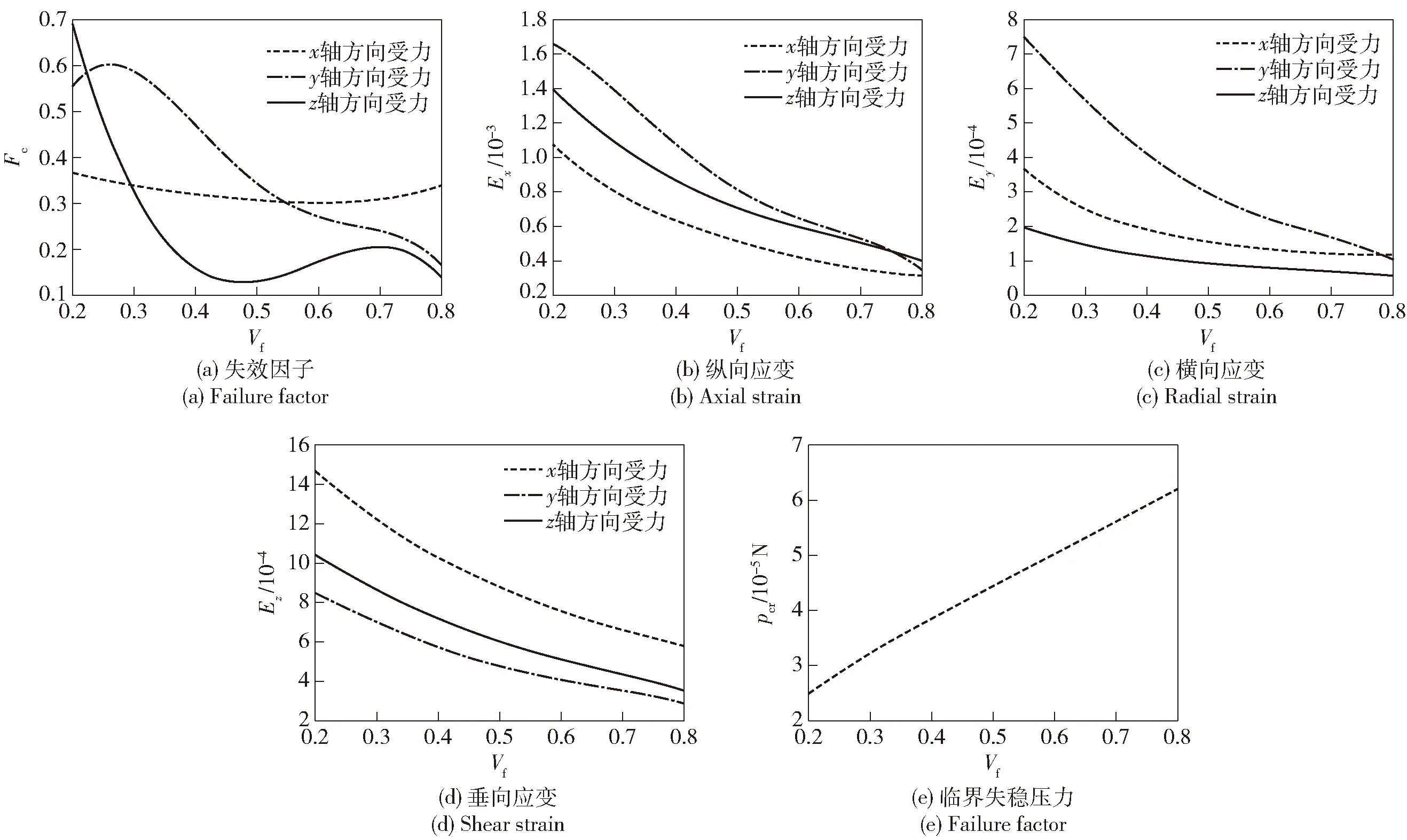
图9 纤维体积分数对导管支臂力学性能影响Fig.9 Effect of fiber volume fraction on mechanical properties of supporting structure

1) 在结构变形方面，随着纤维体积分数的增加，3种受力模式下导管支臂应变下降。表明纤维体积分数的升高，提高了结构的整体刚度。

2) 在结构稳定性方面，支臂结构受垂向压力时，其临界失稳压力随着纤维体积分数的增大而升高，表明提高纤维体积分数有助于改善支臂结构稳定性。

3) 在材料失效方面，3种受力模式下失效指数随纤维体积分数变化规律差异较大：①x轴方向受力时，失效指数变化范围较小，趋势为先降低后上升。可见x轴方向受力时，纤维部分的变化对结构失效性能影响程度较小，与图5(a)中失效指数受基体影响较大相互印证。②y轴方向受力时，失效指数先小幅升高后降低。大的纤维体积分数可以使一定情况下y轴方向受力后失效情况降低。③z轴方向受力时，失效指数总体随纤维体积分数的增加而降低，在一定范围内具有极小值与极大值。这是因为在一定范围内，适当基体占比能够改善复合材料强度性能。复合材料力学性能对增强纤维的强度、刚度敏感，而基体辅助作用同样在结构整体响应中得到体现。

4) 基体在复合材料起到粘接并保持纤维方向作用，力学性能相比于纤维材料较弱，但在整体结构中其作用不可忽略。

3.3 纤维铺设角度对支臂力学性能影响

设导管支臂复合材料铺设方式下各层铺层角为[θ1,θ2,…,θ8]s，16层对称铺设，其中，θ1为最内层和最外层铺层角。图10展示了支臂结构力学响应中铺层角的百分比影响，主要从失效指数、受力方向应变以及顶部受压时的临界失稳压力进行分析。由图10可见：当结构纵向受力时，θ8对失效指数的影响最大，θ1对纵向应变影响最大；当结构横向受力时，θ6对失效指数的影响最大，θ8对横向应变影响最大；当支臂结构端部垂向受力时，对失效指数、垂向应变以及临界失稳压力影响最大的均为θ7。支臂铺层结构采取对称铺设，因此在设计时应对影响较大的铺层进行特殊考虑，以增强其结构性能。