基于二阶等效电路模型的软包锂电池放热特性仿真及试验*
2022-07-04梁桄大李曦陆伟华
梁桄大 李曦 陆伟华
(桂林航天工业学院 汽车工程学院,广西 桂林 541004)
新能源汽车已经成为我国重要战略性新兴行业,其中使用锂电池作为动力来源的新能源车在市场中占据巨大的比重。然而锂电池在汽车行驶过程中的高倍率放电会导致电池包急剧生热,同时锂电池的寿命和安全性受温度影响比较大。
因此为了探索电池内的电化学反应过程与生热量的相互联系,研究者提出了不同的模型进行预测。BERNADI等[1]提出的一维生热模型至今被广泛应用,但该模型不能精确地考虑电池荷电状态对生热量的影响。KWON等[2]基于前人的研究,提出了NTGK模型。该模型借助正负极的相电位、不同放电深度时的电流密度归纳出电化学反应热,是一个半经验的电化学模型。王超等人[3]使用NTGK模型来验证不同充电方式的电化学特性,与实验能较好吻合;CHEN和RINCóN-MORA[4]基于等效电路(equivalent circuit model,ECM)模型提出了一个二阶改进模型,用实验测试了电池的不同参数如开路电压、内阻和电容等,验证了该模型的准确性。
也有许多研究人员直接以实验方式来探究不同条件下电池的放热特性。如李礼夫等[5]通过对方向的磷酸铁锂电池进行恒流充放电的温度测试实验,讨论了电池容量与其温度的动态联系。沈嘉丽等[6]以不同的放电倍率对18650锂电池的表面进行温升实验,分析了圆柱形电池的温度分布状态。李腾等[7]通过仿真与红外热成像的对比,得到了电池表面温度分布的图像,并提出了结构优化建议。
近年来随着计算流体力学(Computer Fluid Dynamics, CFD)的技术发展,不同的物理模型如传热模型、电气模型和流体模型都能在软件中进行耦合求解。成熟的动力电池的设计如丰田普锐斯混合动力汽车的MH-Ni电池组就是在CFD软件中进行设计与优化的[8]。沈帅[9]在Fluent中使用BERNADI的一维生热模型研究了LiFePO4电池的生热散热等温度场变化。RAJIB MAHAMUD[10]将集总热容电池热模型和二维CFD模型耦合起来改善了电池组的温差状况,并以实验的方式进行了对比。
较多文献均证明了电池的多种模型的电气精确度,其中ECM模型的提出是为了解释电池在不同荷电状态下的开路电压、电阻和电热,但目前较少人以实验验证ECM的生热机理是否准确。此外,以实验完成的研究多数是为了分析温度变化,较少结合相应模型讨论,仅有的理论模型采用的是一维或二维的生热模型,没有对比不同荷电状态时的温度变化是否准确。
本文以软包锂电池为对象,通过电池测试技术收集电池的各项参数并进行建模,在CFD软件Fluent中以ECM模型进行电热耦合仿真,通过实验数据与仿真进行对比,以探索ECM模型的电热耦合结果的准确度、电池的生热规律。该研究结果可为后续对电池模组的热管理系统提供数据基础。
1 实验
实验研究的软包电池是三元锂电池,正极材料是镍钴锰酸锂,负极材料为人造石墨,电解液为六氟磷酸锂,额定容量为10 Ah,额定电压为3.7 V,充电上限电压为4.2 V,放电下限电压为3 V,尺寸为13.5 mm×65 mm×132 mm。试验过程是将电池放置于恒温恒湿箱内进行放电实验,记录其特性曲线。恒温恒湿箱选用的型号是新威MGDW-150-40,控制温度的精确度能达到±0.1 ℃。电池测试系统是新威CTE-4008-5V300A,测量电压误差为±0.1 mV,电流误差为±0.1 mA,温度误差为±0.1 ℃。
在电池不同的放电倍率过程中,恒温箱的温度控制在27±0.1 ℃范围内,测试系统通过K型热电偶分别测量电池表面9处的温度变化。为了较普遍地收集电池表面温度特征,同时考虑结构的对称性,温度测点分别布置在顶部3处,正面3处,侧面3处,如图1。电池被隔热材料包裹住,避免热量流失,以便精确地测量生热量,如图2。对电池在进行0.5 C(5 A)、1 C(10 A)与2 C(20 A)三种不同倍率的脉冲放电试验,方案详见表1。

表1 脉冲放电方案

图1 9处热电偶测温布置

图2 电池放电测试
2 数值仿真
2.1 理论模型
充放电时电池生热,表面温度升高,在Fluent软件中通过求解能量方程得到其表面的温度分布。能量方程中热量的产生项来源是电池的欧姆热,即:

(1)
∇·(σ+∇φ+)=-jEch
(2)
∇·(σ-∇φ-)=jEch
(3)

等效电阻模型是将电池视为电阻与电容组成的电路,该模型对于充电与放电都适用。其中等效为一组电阻与电容的模型为一阶模型,等效为两组电阻与电容的为二阶模型,等效为多组的为高阶模型。一阶模型较为简化,其准确性欠缺;高阶的模型较准确但计算复杂,考虑准确性与复杂程度,采用二阶等效模型,如图3。其电路的电压可表示为:
V(t)=Vocv(soc)+V1+V2-Rs(soc)I(t)
(4)
其中:Vocv为开路电压;V1、V2分别是等效电路中的电阻两端的电压;Rs是串联电阻;I是电流。
电压对时间微分,分别有:
(5)
(6)
其中:一、二阶并联电阻R1、R2与一、二阶并联电容C1、C2都是关于荷电状态的变量,其数值可通过实验方式进行测量[11]。
并且荷电状态与电容量QAh、放电电流的关系为:

(7)
电流密度则为:
jECh=I/Vol
(8)
其中:Vol为电池体积。
生热量为:
(9)
其中:U为荷电状态为1时的开路电压。

图3 二阶电容电阻生热模型电路图
通过对方形电池进行放电测试,得到不同SOC时的等效电阻与等效电容,见表2。

表2 0.5 C放电测试中电池的参数
对其进行多项式拟合,可以得到关系式:
Voc(soc)=19.07soc5-60.46soc4+73.92soc3-43.47soc2+12.77soc+2.257
(10)
Rs(soc)=-0.04soc5+0.13soc4-0.16soc3+0.09soc2-0.02soc+0.01
(11)
R1(soc)=3.208soc5-10.3soc4+12.73soc3-7.548soc2+2.246soc+0.489
(12)
R2(soc)=-0.507soc5+1.498soc4-1.721soc3+0.96soc2-0.259soc+0.032
(13)
C1(soc)=3.48×107soc5-9.5×107soc4+1.02×108soc3-5.39×107soc2+1.4×107soc-1.2×106
(14)
C2(soc)=-1.567×105soc5+3.688×105soc4-2.501×105soc3-5412soc2+5.296×104soc-1226
(15)
则电池的二阶ECM模型可以求解。
2.2 仿真模型
Fluent在电热耦合仿真中采用的是有限元方法,将电池模型离散成网格,设定正极的网格中相电位最高,负极最低。通过电池内部的导电率和电阻电容来求解电流密度与电流分布。然后通过计算模型中网格单元的电流密度和电势可以求解其生热量,即欧姆热。得到每一网格中的生热量后可求解能量方程,解出热量传导方向与温度分布等物理场。通过这一电热耦合求解,电池的电热耦合问题得以解出。
在Fluent中划分网格,平均网格体积为8.8×10-5m3,如图4。在电池模型中选择等效电阻模型,根据实验数据分别填写串联电阻,一、二阶并联电阻,一、二阶并联电容。电池的外壳材料为铝,其比热容为903 J/(kg/K),导热系数为238 W/(m·K)。边界条件选择热对流,其对流换热系数为5 W/(m2K)。仿真的初始温度设为27℃,采用瞬态模型。放电时间、放电倍率与静置时间保持与实验一致。

图4 电池网格模型
3 数据对比
3.1 电压
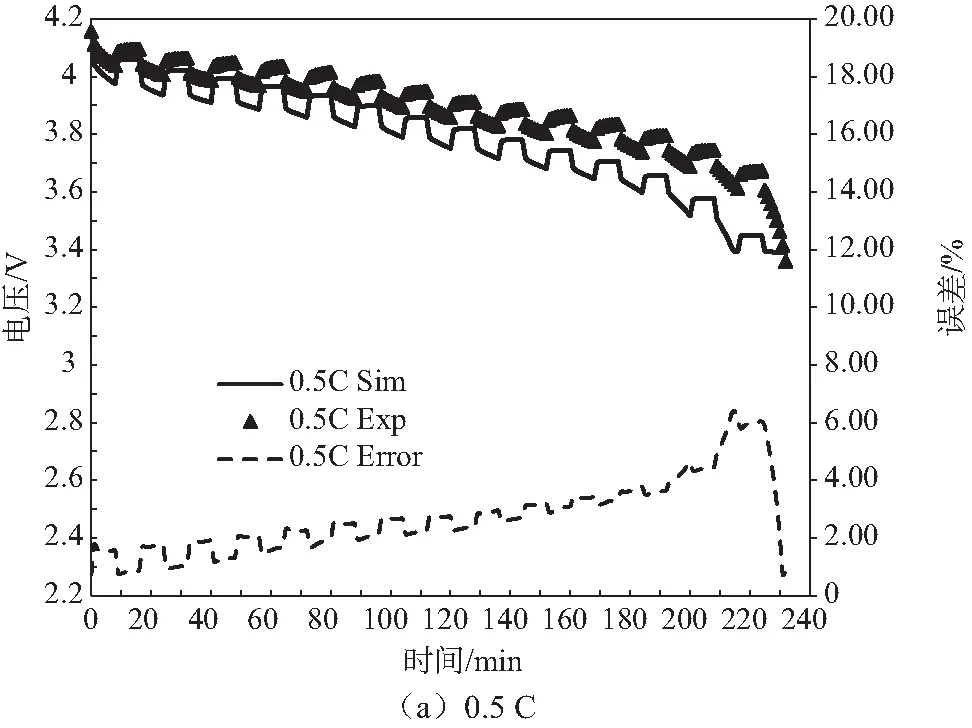
经过仿真与实验的电压对比,如图5,可见其仿真结果较为准确。对电池进行0.5 C放电时,最大误差为6.39%,且1 C放电,2 C放电的误差分别为6.6%和6.5%。该误差的部分来源是模型内源的误差,CHEN[4]测试了10个相同型号的镍氢电池,其模型与实验中电压的误差最大能达到2%。因为采用多项式来拟合电池的参数,还有部分误差的来源是多项式系数的截断误差和拟合误差。
3.2 温度
图6为0.5 C、1 C和2 C时实验与仿真中电池表面温度随时间的变化情况。在实验中对电池表面9处温度值进行多次重复测试并取平均值,在仿真中对电池的表面取平均温度,分别以虚线与实线表示。在图6中可见,随着放电时间增加,电池表面的温度不断上升,在静置过程中,温度下降。较小的放电电流(5 A)时,这一现象不明显,但在较大的放电电流(10 A、20 A)时,这现象比较突出。这是因为在实验过程中,恒温箱保持300.15 K(27 ℃)的温度,而在较小的0.5 C放电下,电池的温差和恒温箱的温差在5 K之内,温差较小,自然对流换热导致的热量损失较小。当采用1 C、2 C放电时,两者温差迅速超过5 K,自然对流换热变明显,热量损失变多,故温度下降较多。

对比3个不同的放电倍率,其实验的最高平均温度分别为303.7 K、307.7 K和317.5 K,仿真的平均温度最高达到303.42 K、307.69 K和316.36 K。可知随着放电电流的增加,其生热量也显著加剧。
在0.5 C、1 C和2 C放电实验过程中,电池表面的最低温度与最高温度差Texp diff分别是0.1 K、0.2 K和0.4 K。在0.5 C、1 C和2 C放电模拟中,最低温度与最高温度差Tsim diff分别是0.09 K、0.17 K和0.25 K。这说明了在高倍率放电时,电池的温度分布不均匀情况较突出。对比0.5 C、1 C和2 C三种放电倍率,其仿真与实验的温度误差分别为0.3 K、0.6 K和1.5 K。这说明在高倍率放电中仿真的误差较明显,这可能是由于高倍率放电时荷电状态变低,内阻随温度升高而升高[12]。而二阶等效模型中的电阻是在0.5 C较低温度时测定的值,模型中没有对应温度修正系数,因此在模拟高倍率较高温度时导致误差增加。

表3 实验与仿真的温度对比
3.3 温度云图
图6为0.5 C、1 C和2 C三个不同放电倍率下放电结束时的温度分布云图,其仿真的过程与实验过程保持一致。三个温度云图都呈现了中间温度高,边缘温度低的分布规律,最低的温度是靠近两极耳处的温度。对比可见,在2 C放电结束时,中间的高温区较集中,这反映了高倍率放电时温度会集中在电池中心区域,其温度梯度会明显增大。

图7 不同放电倍率时仿真的温度云图
4 结论
为了探究软包锂电池的放热特征,建立了电热仿真模型。该研究分别通过电池充放电测试实验和软件建模仿真的方法进行研究,得到了不同放电倍率下的电热特性数据。基于电池充放电测试平台,在不同放电倍率的放电测试中采集了电压、温度的数据。采用Fluent仿真软件对电池进行了建模和仿真,得到了电压变化、温度分布云图的结果。
1)本文通过对比实验与仿真的数据,发现以等效电路模型仿真的电压与实验值的相对误差在0.5 C、1 C和2 C时分别为6.39 %、6.6%和6.5 %;温度误差在0.3 K、0.6 K和1.5 K以内。这些结果说明以二阶等效电路模型来进行电热耦合仿真模拟具有相对的准确性。
2)在0.5 C、1C和2 C放电实验中,电池表面平均温度可高达303.7 K、307.7 K和317.5 K,这说明放电倍率越大,电池表面温升越高,电池的生热量越大。
3)同时在三种不同的放电倍率放电结束后,表面温度的分布都呈现表面集中的规律,但高倍率放电后,温度集中更剧烈。这对热管理系统的温控策略有着良好的揭示作用,如在短期的高耗能状态下针对性地对温度集中区域进行降温,能更低耗更有效。
