基于软边小孔的涡旋光轨道角动量检测研究

庄京秋，熊 晗*，虞天成，陈 静，郑金湖

（1. 苏州科技大学物理科学与技术学院，江苏 苏州 215009；2. 南京电子设备研究所，江苏 南京 210007）

1 引 言

随着无线通信技术的发展，人们对通信网络的带宽容量需求不断增加，但基于频率、波长、偏振态等维度的手段已经无法大规模提升通信系统的容量，因此人们开始将目光转向光波携带的轨道角动量（Orbital Angular Momentum，OAM）上。OAM 具有无限个本征态，理论上可以构建无限维的向量空间，利用此空间可以装载大量信息［1-2］。早在2004 年，Gibson Graham 率先利用携带OAM 的光束进行自由空间中的信息传输，证实了OAM 用于信息传输的可能性［3］。此方法的关键之处在于对OAM 中拓扑荷的数值进行检测，目前常用来检测OAM 的方法主要分为模式转换法、干涉法和衍射法。模式转换法是利用诸如叉状光栅、柱透镜和像散透镜等模式转换器［4-6］，将涡旋光转换为其他类型的光束，从而实现对OAM 的检测，但制造这些检测器件难度相对较大且成本较高。干涉法可以通过观察涡旋光与其共轭光束、平面波、球面波等的干涉图样来判断，或者是观察涡旋光通过动态角双缝后得到的干涉光强变化来判断［7-12］，此法虽然成本较低，但光路调节较为复杂。衍射法是根据涡旋光通过衍射光阑后的衍射图像的特征来检测，相比前面两种方法，衍射法虽然在拓扑荷数检测范围上相对较低，但衍射光路简单，光阑制造容易，且成本较低，具有较广泛的应用前景。

高福海等人在2011 年发现涡旋光的单缝衍射条纹出现了弯曲，根据弯曲的方向及程度可以判断涡旋光的拓扑荷［13］。同年Araujo 等人用三角孔对涡旋光的轨道角动量进行测量，发现衍射分布中会出现随拓扑荷数变化的三角形亮斑阵列，并且亮斑阵列单侧主亮斑的数量减去1 即为涡旋光的拓扑荷阶数，采用三角孔测量的涡旋光拓扑荷阶数范围可达±7［14］。所谓的主亮斑，是指在低阶拓扑荷条件下，衍射分布中归一化强度接近于1 的衍射光斑，接近于0 的则称为次亮斑，随着拓扑荷的阶数增加，主亮斑的归一化强度会不断降低，而次亮斑的则会不断提高。当最外围的主亮斑和相邻次亮斑的相对强度不大时，将无法在衍射分布图中精确识别出主亮斑，此时基于小孔的涡旋光检测手段便达到了极限。同年，Mesquita 等人改用方孔进行测量，发现可以完美测量偶数情况的拓扑荷数，但奇数情况下衍射亮斑的识别度不高［15］。Silva 等人对涡旋光经过正方孔和三角孔的衍射结果进行对比试验，发现当正方孔与三角孔的边长相等时，正方孔的轨道角动量测量范围为三角孔的两倍以上［16］。

为进一步提高基于小孔衍射的涡旋光检测技术，本文研究将硬边小孔改进为具有超高斯阶数的软边小孔，利用软边光阑对衍射光束在一定程度上的抑制作用［17］，来减弱衍射分布四周的次亮斑对主亮斑识别产生的干扰，从而提高衍射分布中主亮斑的可识别度并扩大轨道角动量的检测适用范围。

2 理论与模拟

2.1 拉盖尔-高斯光束衍射后的光强分布

拉盖尔-高斯光束是一种典型的涡旋光束，它自身携带轨道角动量，在极坐标系下的复振幅表达式为［18］：

由于矩孔只能测量单环涡旋光束的OAM，所以取径向指数p=0，L|[2r2ω2(z)]=1，并且将式（1）改写成直角坐标形式：

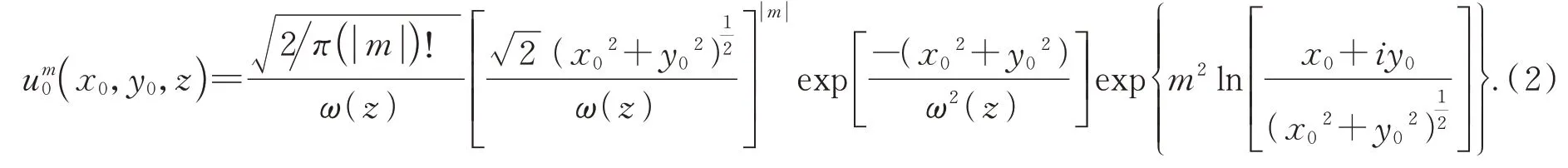
将式（2）代入菲涅耳衍射公式中，在观察平面z处的光场分布为：

以矩形孔为例，硬边矩孔的透过率函数为：

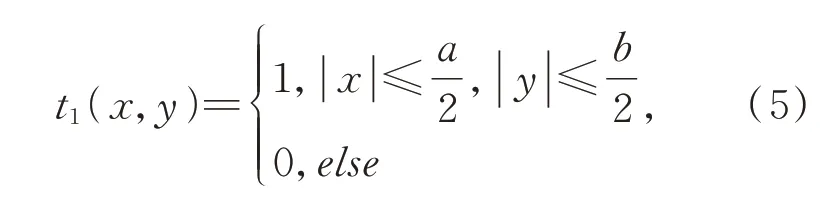
其中，a和b为硬边矩孔的边长。软边矩孔的透过率函数用二维平顶超高斯函数表示为［19］：

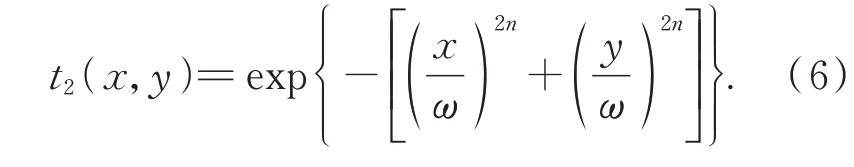
衍射光阑及透过率分布如图1 所示，由图可见，硬边矩孔的透过率只有0 和1，而软边矩孔的透过率分布变化相对平缓。随着超高斯阶数n的增加，相对应的软边区域会随着减少，且趋向于0。这时软边矩孔的光强分布趋向于硬边矩孔。

图1 衍射光阑及透过率分布Fig.1 Diffraction aperture and transmittance distribution

光束通过矩孔后的衍射效果可以从干涉的角度来分析。涡旋光的矩孔衍射图通过上下方向和左右方向的边形成的衍射条纹叠加在一起，干涉形成横竖排列的光点阵列，因此可以将矩孔拆分成单边及多边的组合来依次衍射。这里选用矩孔环，目的是为了验证单边衍射效果，实际上矩孔环和单矩孔的衍射效果类似，并且当矩孔环中的内矩孔越远离外矩孔时，衍射越强烈，因此单矩孔的衍射效果最好。

如果狭缝边是竖向排列的，则衍射场顺时针旋转90°；狭缝边是横向排列的，则衍射场逆时针旋转90°，具体的效果图可由图2 的（a1）～（a2）和（b1）～（b2）所知。有了这个规律后，任意狭缝边组合的衍射图都可知。将硬边矩孔换成软边矩孔，衍射效果也类似，也是单边衍射并相互干涉的结果，并且由于软边矩孔对衍射的抑制作用，光束能量更加集中在中心区域，如图2 所示。值得注意的是，不管是矩形环还是单矩孔，对衍射图起影响作用的只是最外层的边，“外硬内硬”和“外硬内软”的衍射图一样；“外软内软”和“外软内硬”的衍射图一样，因此只需研究单矩孔。

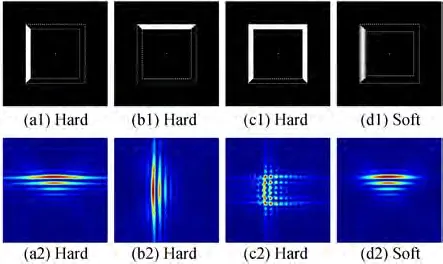
图2 矩孔环的单边衍射效果图Fig.2 Unilateral diffraction effect diagram of a rectangular aperture ring

2.2 矩孔衍射仿真

采用拉盖尔-高斯光束来入射矩孔，波长为632.8 nm，束腰半径为0.5 mm，软边和硬边矩孔的边长均为1.0 mm。由于软边矩孔衍射图样中主、次亮斑的强度对比值受软边矩孔的软化效果影响，软化效果由超高斯阶数决定，为找出合适的超高斯阶数n使得软边矩孔检测涡旋光拓扑荷数的可识别度达到最佳，这里采用两个参数作为评价标准，包括衍射图样中主、次亮斑的强度对比值CPS（Contrast Values of Primary and Secondary Bright Spots Intensity）和主亮斑区域波峰波谷强度平均对比值ACPT（Average Contrast Values of Peak and Trough Intensity）。

其中：P1为最外侧主亮斑强度值，S1为相邻次亮斑强度值，Pi为主亮斑区域第i个波峰值，Ti为主亮斑区域第i个波谷值，N为主亮斑（即波峰）的个数。以图3（a）拓扑荷数为8 的衍射图样为例，取最外侧主亮斑一行数据，得到其横向强度分布曲线图3（b），图中虚线上方为主亮斑区域，下方为次亮斑区域。CPS 值用来表征主亮斑相比次亮斑的对比度，数值越高说明主亮斑越突出；ACPT 值用来表征主亮斑之间的粘连程度，数值越高说明“粘连”现象越不明显。

图3 CPS 和ACPT 计算示例及结果Fig.3 Calculation examples and results of CPS and ACPT

这里分别以拓扑荷数m从1 取到30，超高斯阶数n从2 取到30，计算软边矩孔衍射图样中主、次亮斑的强度对比值和主亮斑区域波峰波谷强度平均对比值，得到图3（c）、（d），右侧的颜色栏表示当前颜色下的CPS 和ACPT 数值。由图可知在同种拓扑荷数下，主、次亮斑强度对比值随着超高斯阶数的降低而增加，主亮斑区域波峰、波谷强度平均对比值随着超高斯阶数的增加而增加。要想软边矩孔检测涡旋光拓扑荷数的可识别度达到最佳，需要保证主亮斑相比次亮斑更加突出的同时主亮斑之间粘连程度足够低。所以将图3（c）、（d）的值一一对应相加得到组合对比值，依次寻找每种拓扑荷数下组合对比值最大所对应的超高斯阶数，作为当前拓扑荷数下的最佳阶数，最后取它们的平均值，作为一个通用型超高斯阶数，以尽量适合大部分的拓扑荷数。

图4 为超高斯阶数取值过低和过高的衍射图。如图4（a）所示，对于过低的超高斯阶数，衍射图中次亮斑的归一化强度值虽然降低，但主亮斑之间的“粘连”现象严重，识别度不高，并且此时的主、次亮斑强度对比值过大，容易在取最大组合对比值所对应的超高斯阶数时产生干扰。如图4（b）所示，对于过高的超高斯阶数，其衍射效果接近硬边矩孔，主亮斑之间“粘连”现象不明显，但主亮斑与次亮斑的对比度降低。以上两种情况人眼能直接观察分辨出，因此需要对每种拓扑荷数的情况依次分辨，如拓扑荷数为10 时，阶数低于6 和高于18 的情况以及拓扑荷数为20时，阶数低于8 和高于20 的情况需要先排除在外，再来寻找组合对比值最大时所对应的超高斯阶数，结果如图5 所示，最后算得平均超高斯阶数n约为14，以平均超高斯阶数14 来构建软边矩孔。

图4 超高斯阶数取值过低和过高的衍射图Fig.4 Diffraction patterns for too low and too high Gaussian orders

图5 不同拓扑荷数下，最大组合对比值所对应的超高斯阶数Fig.5 Gaussian order corresponding to the maximum combined contrast value under different topological charges

取不同拓扑荷数的拉盖尔-高斯光分别经过硬边矩孔和软边矩孔（对应14 阶的超高斯阶数）衍射，得到如图6 所示的衍射图及横向光强分布曲线。图6 下图中超过虚线的为中心主亮斑区域，低于虚线的为周边次亮斑区域；实线箭头指向的是最外围主亮斑，虚线箭头指向的是与外围主亮斑相邻的次亮斑，数字代表归一化的相对强度。

图6 不同拓扑荷数下硬边和软边矩孔衍射图及横向光强分布曲线Fig.6 Diffraction patterns of rectangular aperture with hard-edge or soft-edge and lateral light intensity distribution curves under different topological charges

由图6（a）和（d）可见，当涡旋光拓扑荷数m为8 时，采用硬边矩孔的衍射光强分布中最外围主亮斑的归一化强度值为1.00，相邻次亮斑的归一化强度值约为0.32，两者的强度对比值达到3.13，此时中心区域的主亮斑群在衍射分布中极易辨别。采用软边矩孔的衍射分布中最外围的主亮斑归一化强度值也为1.00，相邻次亮斑的归一化强度值约为0.27，两者的强度对比值达到3.70，相比硬边矩孔的3.13 提高了约18%，使得主亮斑群具有更高的辨识度。同样地，由图6（b）、（e）可见，当拓扑荷数m取14 时，软边矩孔相邻主、次亮斑的强度对比值为2.17，相比硬边矩孔的1.78 提高了约22%；当拓扑荷数m取20 时，软边矩孔主、次亮斑的强度对比值相较硬边矩孔提高了约26%。模拟结果表明：当涡旋光拓扑荷数取值逐渐提高时，中心区域主亮斑相比周边次亮斑的能量对比值逐渐下降，直至无法区分时便达到检测范围的极限，由于软边矩孔可以通过增加中心区域主亮斑的能量占比，降低周围次亮斑的能量占比从而提高主亮斑的可识别度，同种拓扑荷数下软边矩孔主亮斑的能量占比和可识别性相比硬边矩孔而言有所提升，由此拓展矩孔光阑的涡旋光检测范围。

2.3 三角孔衍射仿真

软边光阑同样适用于基于其它形状小孔的涡旋光拓扑荷数检测，这里采用一维平顶超高斯函数来构建软边三角孔（阶数取根据软边三角孔主、次亮斑强度对比值优化后得到的平均超高斯阶数12），硬边和软边三角孔的边长均取1.0 mm，涡旋光的参数和上文矩孔衍射仿真中保持一致，得到如图7 所示的衍射图和横向光强分布曲线。发现m=5 时，软边三角孔相比硬边三角孔的主、次亮斑强度对比值提高了约14%，m=10 时提高了约21%，主、次亮斑强度对比值的提高效果与矩孔光阑类似，所以对于其他类型的小孔光阑，都可以使它们软边化，以此来提高拓扑荷数的检测范围和主亮斑的可识别度。此外，硬边三角孔可以检测拓扑荷数互为相反数的涡旋光，负数情况下衍射图会旋转180°，这点上软边三角孔也一样。硬边三角孔最高只能检测拓扑荷数为±10的涡旋光束，而采用软边三角孔在此基础上可将检测范围拓展到±20 阶。

图7 硬边和软边三角孔的衍射图及横向光强分布曲线Fig.7 Diffraction pattern and lateral light intensity distribution curve of triangular aperture with hard-edge or soft-edge

3 实验设计与分析

3.1 实验装置

图8 为实验光路的示意图。氦氖激光器发出中心波长为632.8 nm 的激光，经显微物镜MO、针孔PA、透镜L1 进行准直扩束和滤波，并通过偏振片P 将光束偏振方向调制到空间光调制器SLM 液晶面的偏振方向，SLM 上加载涡旋光干涉形成的叉状光栅相位图，经过调制产生的多级涡旋光经分束立方体BS 反射后经过透镜L2，在透镜L2 的焦平面处放置一个圆形光阑CA，用来筛选正一级或负一级涡旋光，筛选出的涡旋光再经透镜L3 缩束到和衍射矩孔DA 的尺寸相匹配，经DA 衍射和透镜L4 后，其远场衍射分布利用CCD 采集。

图8 涡旋光经硬边和软边矩孔衍射的实验光路示意图Fig.8 Schematic diagram of the experimental light path of the vortex beams diffracted by rectangular aperture with hardedge or soft-edge

常见的软边光阑有乳胶型、玻璃磨砂型和锯齿型等［20-23］，其中锯齿型就是将原来的硬边进行锯齿化处理，制作相对简单，批量制作成本低，也是本文所选用的软边矩孔加工类型。图9 是制作的硬边和软边矩孔实物图及实验光路图，在一块金属薄片上用激光雕刻出直边或锯齿边矩孔，边长均为1.0 mm。按照光路示意图搭建的实验光路如图9（a）所示。

图9 实验光路图及矩孔实物图Fig.9 Experimental light path diagram and physical diagram of rectangular aperture

3.2 实验分析

在SLM 上依次加载拓扑荷数m=8、m=14和m=20 的叉状光栅相位图，产生的涡旋光分别经硬边和软边矩孔形成衍射分布，提取同一行位置的衍射光强分布，可以得到一维的光强分布曲线，并以此计算主、次亮斑的强度对比值。如图10所示，当m=8 时，从软边矩孔的衍射图中能直接观察到各个主亮斑之间的间距较大，清晰可辨，而硬边矩孔的衍射图中主亮斑则有些粘连在一起，不容易分辨，主、次亮斑强度对比值上，软边矩孔为4.11，硬边矩孔为3.61，软边相比硬边提高了约14%；m=14 时，软边矩孔衍射图中的主亮斑虽然不像m=8 中分隔的那么明显，但其主、次亮斑强度对比值2.27 相比硬边的1.93 依旧提高了约18%。同样的，m=20 时硬边矩孔的主、次亮斑强度对比值只有1.52，而软边矩孔则有1.85，软边相比硬边也提高了约22%。实验与仿真对比结果如表1 所示，可见在测量值和随拓扑荷数的变化趋势上，实验结果与仿真结果是相符合的。

表1 采用软边和硬边矩孔的涡旋光衍射分布中主、次亮斑强度对比值仿真和实验结果Tab.1 Simulative and experimental contrast value of the primary and secondary bright spot intensities in the diffraction distribution of the rectangular aperture with hard-edge or soft-edge

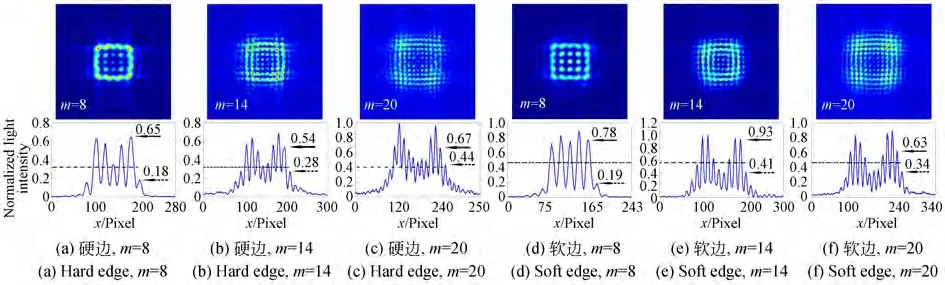
图10 不同拓扑荷数下硬边和软边矩孔实验衍射图及横向光强分布曲线Fig.10 Experimental diffraction patterns and lateral light intensity distribution curves of rectangular aperture with hardedge or soft-edge under different topological charges

取拓扑荷数从1 取到30 的涡旋光分别经硬边和软边矩孔，同时计算它们的主、次亮斑强度对比值和提高量，结果如图11 所示，可以发现不同拓扑荷数情况下主、次亮斑强度对比值和提高量都不同。当拓扑荷数较低时（m＜10），硬边矩孔的主、次亮斑强度对比值基本都在2.0 及以上，衍射图中主亮斑的识别度很高；而当拓扑荷数较高时（10＜m＜20），硬边矩孔的主、次亮斑强度对比值逐渐下降；拓扑荷数大于20 时，其主、次亮斑强度对比值只有1.3 左右，结果就是硬边矩孔对于拓扑荷数大于20 阶的涡旋光，主亮斑的识别度降低。软边矩孔在低阶和高阶拓扑荷数情况下，其主、次亮斑强度对比值都能维持1.6 以上，证明了同种拓扑荷数下，软边矩孔得到的涡旋光衍射图相比硬边矩孔有着更高的主亮斑识别度。

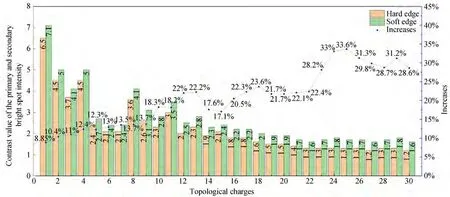
图11 实验得到的硬边和软边矩孔衍射图中主、次亮斑强度对比值和提高量Fig.11 Contrast value and increase of the primary and secondary bright spot intensity in the diffraction pattern of the rectangular aperture with hard-edge or soft-edge obtained from the experiment

此外，取部分拓扑荷数下硬边和软边矩孔实验衍射图，如图12，发现当拓扑荷数取2 和4 时，软边矩孔衍射图中的各个主亮斑之间的间距更大，无粘连现象，相比硬边矩孔识别度更高；拓扑荷数取3 和5 时，软边矩孔衍射图中四个角上的两个主亮斑会更加容易分辨，不像硬边矩孔中会误以为只有一个主亮斑，这样对于低阶奇数情况拓扑荷数的涡旋光有更高的识别度。此外对于矩形孔，拓扑荷数互为相反数的衍射图旋转180°不会有区别，所以矩形小孔无法区分正负涡旋光。硬边矩孔最高测得的拓扑荷数为20，而采用软边矩孔，则可以进一步测到30 阶。

图12 不同拓扑荷数下硬边和软边矩孔实验衍射图Fig.12 Experimental diffraction patterns of rectangular aperture with hard-edge or soft-edge under different topological charges

将实验和仿真得到的硬边和软边矩孔衍射图的主、次亮斑强度对比值提高量进行对比（软边矩孔阶数取优化后n=12），如图13，可以发现，实验与仿真的结果类似，低阶拓扑荷数下提高量不大，这是因为原本硬边矩孔的衍射图中主亮斑的可识别度已经很高，软边矩孔作用不明显。随着拓扑荷数的增加，硬边衍射图中主亮斑的可识别度降低，这时采用软边，能增大主亮斑的可识别度，并且提高量逐渐增加，但也将趋于饱和，不能无限地提高。对于低价拓扑荷数（m≤10），仿真中主、次亮斑的强度对比值平均提高量为14.9%，实验为12.9%；中阶（11≤m≤20）情况，仿真为20.4%，实验为20.7%；高阶（21≤m≤30）情况，仿真为23.8%，实验为28.9%，说明了软边矩孔对于中高阶拓扑荷数涡旋光（m≥10）的主亮斑可识别度提高效果更为明显。此外由图可看出部分仿真的主、次亮斑强度对比值提高量高于实验，部分低于实验，两者RMSE 值约为4.87%，存在一定偏差。出现这种情况，一方面可能是加工完成的软边矩孔阶数和仿真不是完全对应，并且锯齿的加工精度不高；另一方面可能是在光路调试过程中，滤波后的光束近场质量欠佳，造成涡旋光的光强分布不均匀，且涡旋光与矩孔不是完全正对中心，造成衍射光强分布不均匀。

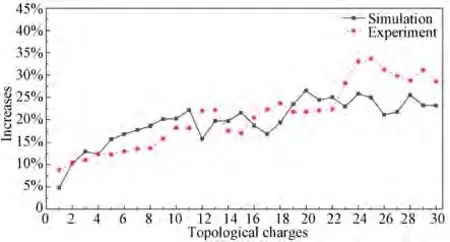
图13 实验和仿真的主、次亮斑强度对比值提高量Fig.13 Increase in the contrast value of the primary and secondary bright spot intensity of the experiment and simulation

4 结 论

本文从理论模拟和实验上研究了基于软边小孔的涡旋光轨道角动量检测技术。由于软边对光束衍射具有一定抑制效应，能够提高涡旋光的远场衍射分布中主亮斑的可识别度和拓扑荷数的可检测范围。由于不同的超高斯阶数具有不同的提高效果，采用波长632.8 nm、束腰半径0.5 mm 的拉盖尔-高斯光束来入射边长1.0 mm的软边和硬边矩孔，通过模拟计算在不同的拓扑荷数（1～30 阶）和超高斯阶数（对应阶数2～30阶）的条件下，软边矩孔衍射得到的主、次亮斑的强度对比值和主亮斑区域波峰、波谷强度平均对比值来选取合适的超高斯阶数以达到最佳的检测效果，并获得了对应超高斯阶数为14 的优化软边矩孔，由此将涡旋光轨道角动量的测量范围从硬边矩孔的20 阶拓展到30 阶；对于软边三角孔，同样计算出超高斯阶数为12 的优化软边三角孔，将测量范围从硬边三角孔的±10 阶拓展到±20阶。实验上采用了锯齿型的软边矩孔，其结果与模拟仿真结果基本一致。