水下激光通信弱光信号的自适应随机共振检测
2022-07-04张建磊贺锋涛朱云周
张建磊,兰 香,杨 祎,贺锋涛,朱云周
(1. 西安邮电大学电子工程学院,陕西 西安 710121;2. 中国科学院西安精密机械研究所,陕西 西安 710077;3. 水下信息与控制重点实验室,陕西 西安 710077)
1 引 言
近年来,随着人类对海洋勘探、海底监测和海洋资源开发的日益增加,水下无线光通信(Underwater Optical Wireless Communication,UOWC)凭借其传输速率高、通信带宽大、时延小、保密性强等多个显著优势,受到人们的广泛关注和研究[1-3]。由于海水信道环境复杂,光波在传输过程中易受海水吸收和散射的影响,造成光信号的严重衰减[4-6],经过长距离传输后接收端的光功率低于纳瓦量级,光信号可能被淹没在强噪声中无法检测,从而影响水下光通信的系统性能。
为了提升UOWC 的传输速率和传输距离,Shen 等人[7]提出一种基于脉冲位置调制(Pulse Position Modulation,PPM)和多像素光子计数器(Multi Pixel Photon Counter,MPPC)的UOWC系统,并进行了水下信道超低发射功率的实验验证,在接收光功率低至-39.2 dBm 时可实现无误差通信。Wang 等人[8]提出一种以MPPC 作为接收机,采用正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术的UOWC系统,通过实验验证了此系统可以实现3 1 2. 0 3 M b/s 的数据传输速率,且误码率低于前向纠错的限制。Hu 等人[9]设计了一种使用光子计数接收器的长距离水下激光通信系统,并在接收系统中考虑了背景噪声和帧同步的影响,实现3.32 比特/光子的接收性能。目前通过对水下弱光信号进行检测来提升系统性能也有相关研究,Chen 等人[10]设计了一种包含部分响应滤波和格型编码调制技术的联合数字信号处理方案,抑制了均衡器引起的噪声,减少了信号的失真。Hao 等人[11]提出一种改进的决策反馈均衡算法实现弱光信号的检测,且该算法收敛速度快,稳态误差小,信噪比可提升约6 dB。Liu 等人[12]利用能量检测算法提高误码率性能,使用最小平均误差概率准则,并根据曼彻斯特编码特性在接收机中添加控制模块,进一步对符号的起始位置进行校正,信噪比可提升约3 dB。近年来,随机共振(Stochastic Resonance,SR)检测方法因其特殊的检测机制而应用于各个领域,它通过一个非线性系统将噪声的部分能量转化为信号能量,进而增强有用信号[13-14]。Ma 等人[15]通过仿真分析了随机共振系统参数对水下无线光通信系统误码率的影响,初步验证了随机共振检测对水下弱光信号的适用性。Feng 等人[16]提出一种基于随机共振非线性动力学的自适应随机共振方案,将归一化尺度变换应用于随机共振检测,通过噪声方差估计实现随机共振系统参数的自适应调节,但系统初始参数需要人为选定,且系统性能依赖于系统初始参数的选择。
为了进一步验证随机共振对水下弱光信号检测的优异性能,本文通过分析水下弱光信号的特点及随机共振的检测机理,设计了一种基于自适应随机共振的水下弱光信号检测方法,使用改进蚁群算法对随机共振的系统参数进行优化,将输出信号信噪比作为目标函数,动态的调整系统参数,进一步实现随机共振参数的自适应估计。最后搭建了UOWC 系统实验平台,并对实际采集数据进行检测,进一步验证了该方案的优异性能。
2 随机共振对水下弱光信号的适用性
2.1 海水信道光信号传输模型
图1为UOWC 光信号传输模型。由于海水信道复杂,光信号在传输过程中易受水体吸收和散射的影响,导致光信号严重衰减。水下无线光通信功率衰减模型为:
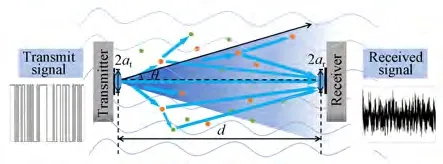
图1 UOWC 光信号传输模型Fig.1 UOWC optical signal transmission model

其中:θ为光源的发散角;at为光学发射天线的孔径半径;ar为光学接收天线的孔径半径;Piexp [-c(λ)d]为Beer-Lamber 定律描述的水下光信号的吸收和散射模型[17];Pi为发射光功率;d为传输距离;c(λ)为衰减系数,包括吸收系数a(λ)和散射系数b(λ)。由于水下信道衰减效应显著,当光信号经过长距离传输或水质较差时,接收端的光功率甚至低于纳瓦量级,此外受系统噪声干扰,光电探测器的输出信号可能被淹没在强噪声中无法准确获取有效信息,进而影响整个通信系统的性能。
2.2 双稳态随机共振
随机共振是信号、噪声和非线性系统共同作用形成的一种非线性现象。双稳态随机共振系统可用Langevin 方程描述[18-19]:
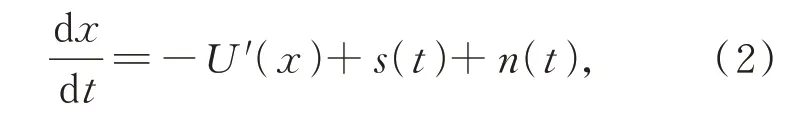
其中:s(t)为输入信号;n(t)是均值为0、强度为D的高斯白噪声,且满足均值n(t) =0,自相关函数n(t)n(0) =2Dδ(t);U(x)为没有信号和噪声输入时双稳态系统的势函数,U′(x)为势函数U(x)的导数,势函数U(x)为:

整理得,
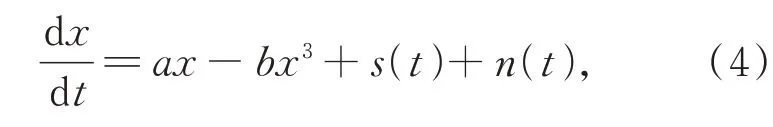


图2 双稳态随机共振势函数Fig.2 Bistable stochastic resonance potential function


双稳态随机共振的阱内活动以及势垒高度对随机共振的产生有重要影响,势垒高度关系着系统产生协同效应时信号与噪声所需的能量,系统阈值Ac大小关系着粒子的跃迁概率,根据双稳态系统的势函数U(x)和系统阈值Ac可知,系统参数a,b会改变势垒高度和系统阈值,进而影响双稳态随机共振。图3 所示为参数a,b对势函数U(x)的影响,势垒越低、阱间距离越小,系统产生随机共振所需的能量越少。图4 所示为参数a,b对系统阈值Ac的影响,Ac的值越大,即粒子越过势垒所需的能量就越多。
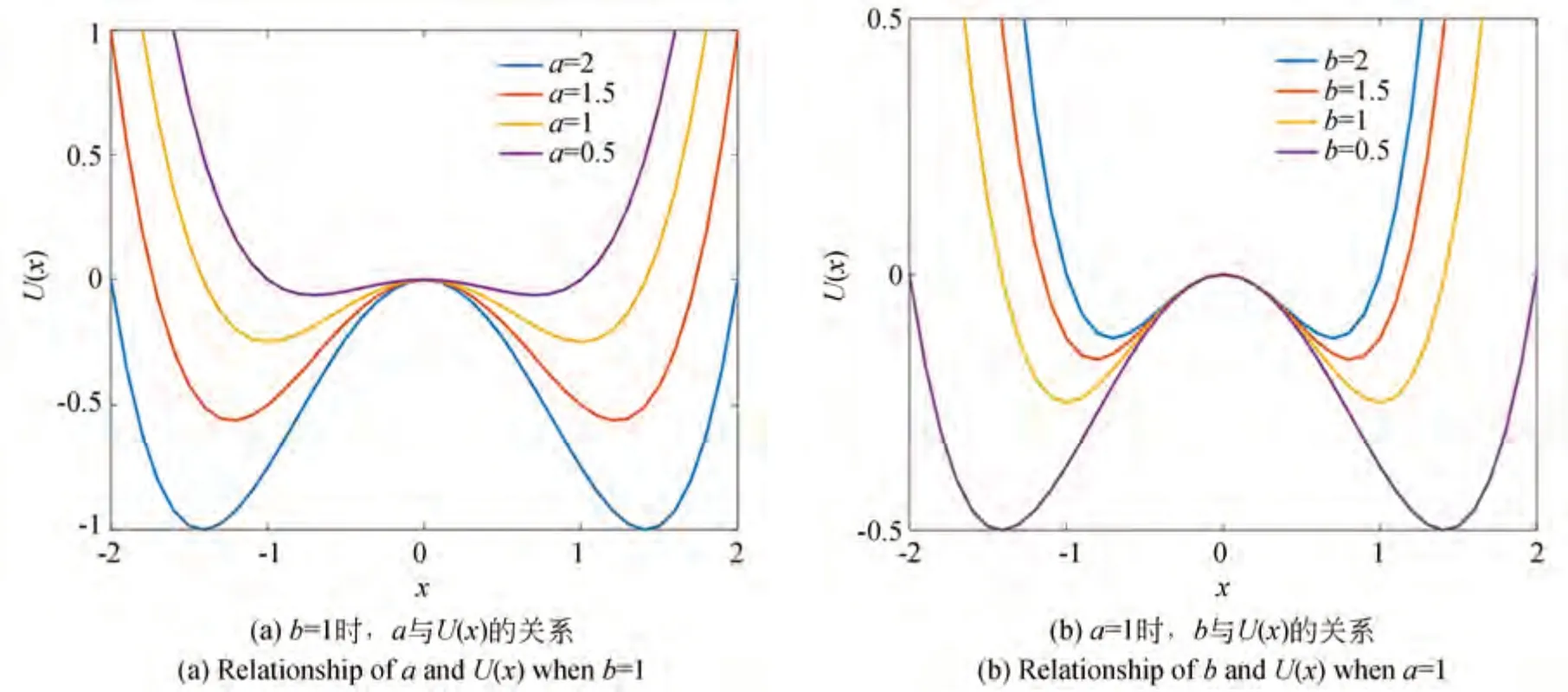
图3 参数a,b 对势函数U(x)的影响Fig.3 Effect of parameter a,b on the potential function U(x)
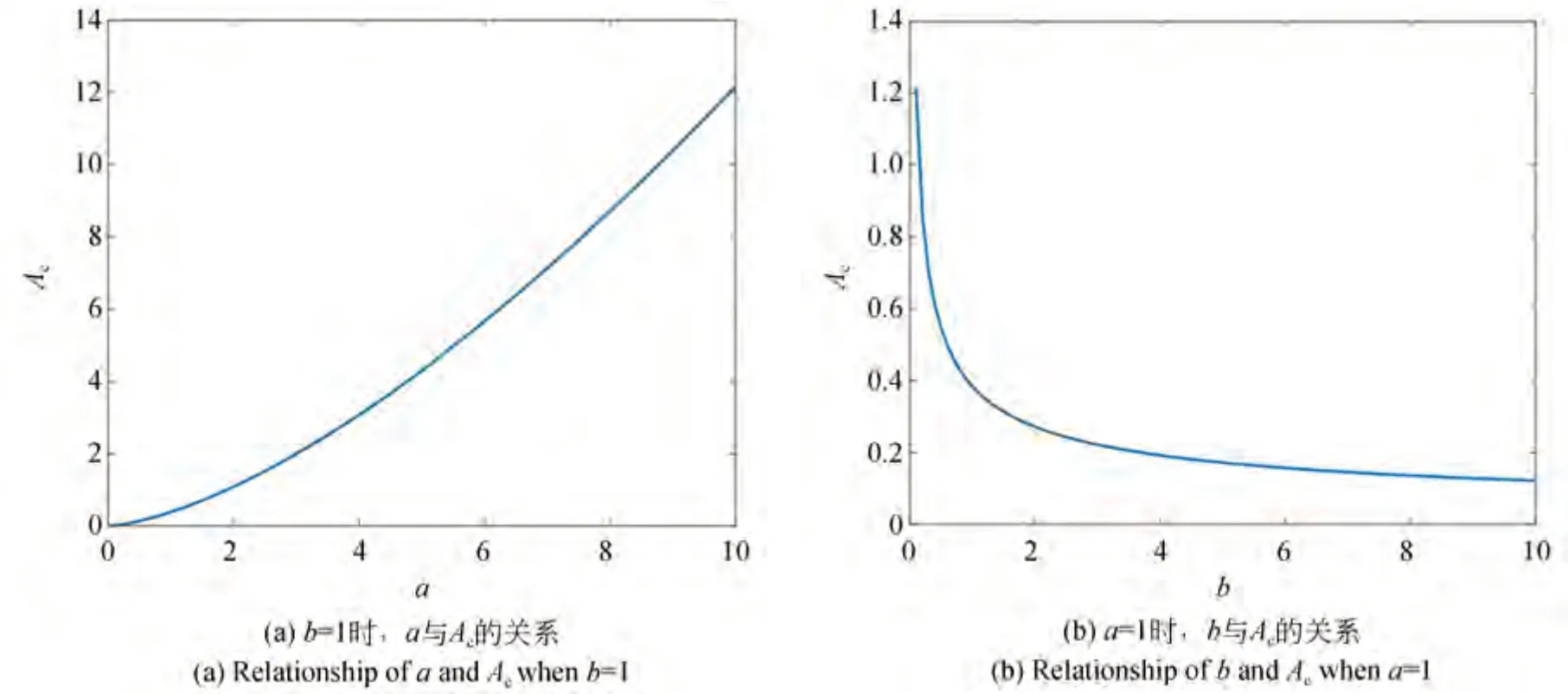
图4 参数a,b 对系统阈值Ac的影响Fig.4 Effect of parameter a,b on the system threshold Ac

此外,由于式(4)不存在精确的解析表达式,所以采用四阶龙格-库塔算法进行仿真求解,计算过程如式(6)表示[20]。其中:pn是系统输入信号s(t)+n(t)的第n个采样点,xn是系统输出信号x(t)的第n个采样点,fs为采样频率,h=1/fs为采样步长。
2.3 二次采样随机共振
由于绝热近似理论的限制,随机共振只能处理频率小于1 的小参数信号。在UOWC 系统中光信号频率不满足绝热近似条件,为了克服小参数信号的局限性,引入二次采样随机共振[21],通过设置变尺度系数,对信号进行频率时间尺度的变换,经过这一变尺度预处理后得到的信号就能满足小参数条件,再将其输入双稳态SR 系统即可实现信号检测,如图5 所示。

图5 二次采样随机共振Fig.5 Secondary sampling stochastic resonance
二次采样的实质是将一个高频率转换为一个低频率的过程。根据信号频率,选择变尺度系数R,fsr表示变尺度采样频率,数值上定义为,

龙格-库塔法的步长h=1/fs变为hr=1/fsr=R/fs=Rh。利用步长可求解输出响应,最后按变尺度系数R恢复原始数据即可。

图6 大参数信号随机共振Fig.6 Large parameter signal stochastic resonance
3 自适应随机共振
3.1 蚁群算法
蚁群算法(Ant Colony Algorithm,ACA)最早是由意大利学者Dorigo 等于1991 年提出的一种寻找最优路径的几率型算法[22],其灵感来源于蚂蚁在寻找食物过程中利用信息素正反馈寻找最优路径,最初是用于旅行商问题。由于它易与其它算法结合,具有较强的鲁棒性,现已大量应用于组合优化问题中。基本蚁群算法步骤如下:
(1)初始化。在计算之初对相关的参数进行初始化,如种群大小m,最大循环次数nitermax,信息素因子α,启发函数因子β,信息素挥发因子ρ等。
(2)构建解空间。将蚂蚁随机放置于不同的出发点,蚂蚁个体根据各条路径上的信息素浓度和路径的启发信息来计算状态转移概率,进而选择下一个节点,t时刻蚂蚁由节点i转移到节点j的状态转移概率Pijk(t)如式(8)所示:
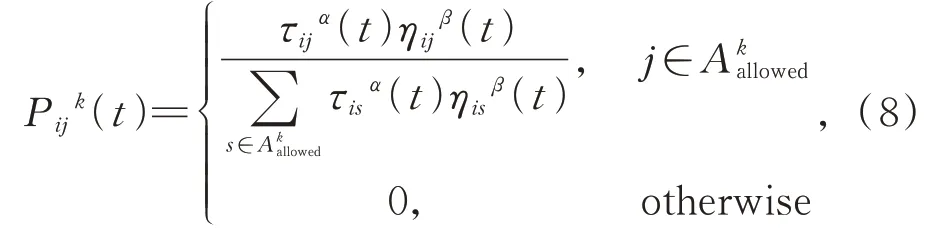
其中:τij为节点i和节点j两个位置之间的信息素浓度;ηij为启发信息,表示为节点i和j之间距离的倒数;α和β为常数,分别表示信息素浓度和启发信息的影响程度;Aowed为未访问过的节点的集合。
(3)更新信息素。蚂蚁每完成一次搜索过程,就会进行一次信息素的更新,更新公式如式(9)所示:
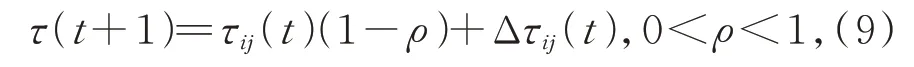
其中:Δτij为蚂蚁从节点i到节点j路径上留下的信息素总和。
(4)判断是否终止。若循环次数小于最大循环次数,则迭代次数加1,清空蚂蚁经过路径的记录表,并返回步骤(2),否则终止计算,输出最优解。
3.2 改进蚁群算法
基本蚁群算法存在容易早熟、停滞、陷入局部最优等不足。针对蚁群算法的这些不足,提出一种基于拥挤度因子的蚁群算法(Improved Ant Colony Algorithm based on Congestion Factor,CFACA)。在人工鱼群算法中,拥挤度的设置是为了防止鱼群在寻找食物的过程中过于集中在一个区域,导致之后的鱼群没有食物可寻的情况发生[23]。将鱼群算法中拥挤度的概念引入到蚁群算法中,根据拥挤度的限制,可以保证大部分蚂蚁不受信息素浓度的影响进行随机寻优,从而提高算法全局搜索的能力。
蚂蚁按照式(8)转移概率选择下一节点后,计算该路径此时的拥挤度Qij,如式(10)所示:



其中:c为拥挤度因子的变化系数,如式(12)所示:
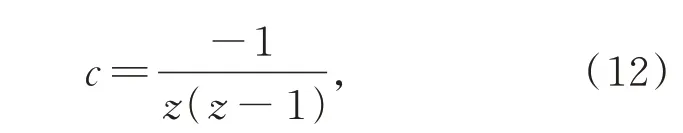
其中:z为路径节点的总数。
3.3 基于CFACA 的自适应随机共振
传统的随机共振进行微弱信号检测时,系统参数大多是人为设置,或者进行单参数优化,这些方法没有考虑到系统参数之间的相互作用,导致最终的检测结果具有一定的偶然性。因此,实现自适应随机共振,可以有效提高系统检测性能。将CFACA 用于优化随机共振系统最优参数的问题中,可以根据检测性能动态的调整系统参数,以达到最优的匹配效果。系统的输出信噪比是衡量随机共振效应的重要指标,信噪比越大则随机共振的输出效果越好。选取输出信噪比作为CFACA 的目标函数,搜索在SNRout取得最大值时最优的系统参数a和b,实现基于CFACA的自适应随机共振。具体步骤如下:
(1)对获取的带噪弱光信号进行预处理。由于光信号的传输频率和采样频率可达到MHz 或GHz 量级,因此不满足随机共振的绝热近似条件。此时,进行二次采样得到小参数信号,使其满足随机共振的小参数输入条件。
(2)划分搜索网格。设定优化参数的取值范围,根据一定的步长分割,划分成若干大小相同的网格。随机在网格节点处放置蚂蚁,且每个节点对应一组随机共振的系统参数(a,b),根据节点可以计算目标函数值。
(3)计算转移概率。每组节点对应的信息素浓度计算相应的状态转移概率,根据概率值的大小选择蚂蚁下一个移动的节点。
(4)计算拥挤度。计算当前节点到蚂蚁选择的下一个节点路径上的拥挤度,若拥挤度小于拥挤度因子,则选择该节点继续走,若拥挤度大于或等于拥挤度因子,则重新选择节点。
(5)优化、更新信息素浓度。根据目标函数输出信噪比更新信息素浓度,计算新的转移概率,并判断蚂蚁觅食所选节点是否收敛。若收敛,找出信息素浓度最高的网格节点,否则跳至步骤(3),继续搜索最优节点。
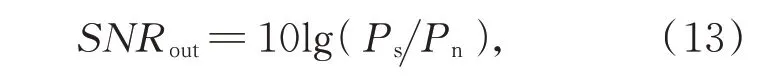
其中:Ps为信号功率,Pn为噪声功率。
(6)判断移动次数。蚂蚁移动次数达到预设的最大移动次数nmax,则输出全局最佳的网格节点,此节点即为随机共振的最优系统参数。
(7)双稳态随机共振。将最优系统参数(a,b)代入双稳态随机共振系统,利用四阶龙格-库塔法求解输出响应,实现弱光信号的检测。
现对ACA-ASR 和CFACA-ASR 检测算法进行复杂度分析,即算法的时间复杂度和空间复杂度。通过分析计算ACA-ASR 算法的时间复杂度为O(m·n)+O(nitermax·m2·n2),CFACAASR 算法的时间复杂度为O(m·n)+O(nitermax·m3·n2)。其中,nitermax为最大迭代次数,m为蚁群数量,n为检测信号的总码元数。对算法各步骤的综合分析,ACA-ASR 算法的空间复杂度为O(n2)+O(n·m),CFACA-ASR 算法的空间复杂度为O(n2)+O(n·2·m)。相较于ACA-ASR检测算法,CFACA-ASR 检测算法增加了拥挤度比较进一步解决局部最优解问题,所以在时间和空间复杂度上相对有所增加。
4 仿真分析
为了验证基于CFACA 的自适应随机共振系统的有效性,采用所建立系统对仿真信号进行分析。图7 所示为使用CFACA 算法完成双稳态系统参数a,b的最优值寻找并处理含有高斯白噪声的伪随机序列的结果,输入信号为双极性信号,仿真码元个数为106个,每个码元的采样点数为100 个,信噪比为-20 dB,系统参数a和b的寻优范围均为[0,5],蚁群规模为m=300,最大迭代次数nitermax=100。图8 和图9 分别为使用ACA 算法和CFACA 算法进行寻优参数时的收敛图。横坐标为迭代次数,纵坐标为目标函数,即输出信噪比。从图中可以看出使用CFACA检测算法时,收敛速度相较于ACA 算法有所提升,且使用CFACA 算法寻优26 次,就可找到系统最优参数,此时寻找到的最优参数为a=0,b=2.448 0,输出信噪比为SNRout=-1.152 5 dB,相比于输入信噪比提高了18.847 5 dB。

图7 基于CFACA-ASR 系统处理的含有高斯白噪声的双极性信号(SNR=-20 dB)Fig.7 Bipolar signal with Gaussian white noise processed by CFACA-ASR system(SNR=-20 dB)
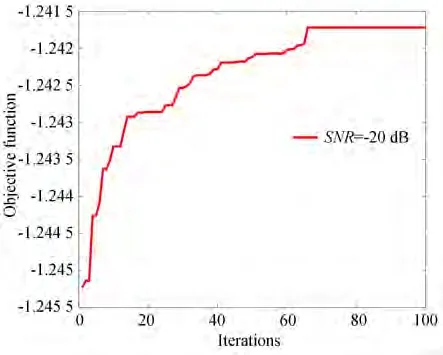
图8 ACA 算法收敛图Fig.8 ACA algorithm convergence graph
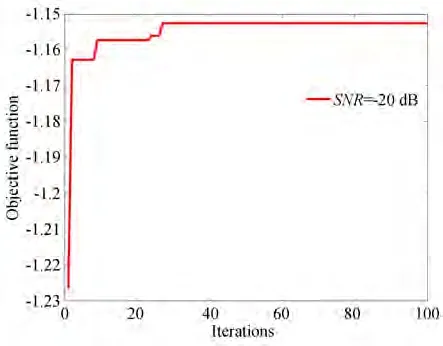
图9 CFACA 算法收敛图Fig.9 CFACA algorithm convergence graph
此外,基于蚁群算法的自适应随机共振(ACA-ASR)检测系统在故障诊断中已实现了微弱特征增强和提取[24],在本文中,也进一步验证了此检测方案对水下无线光通信系统中弱光信号的适用性,并将ACA-ASR 检测方案和恒参SR 检测方案作为对照组,图10 给出了不同输入信噪比SNRin下不经过随机共振(NO-SR)以及分别采用恒参随机共振SR(a=1,b=1)、ACAASR 和CFACA-ASR 的检测结果。

图10 不同检测方案的误码率Fig.10 Bit error rate of different detection schemes
码元个数为106,传输速率为1 MHz,且每个码元的采样点数为100。在低信噪比下,不经过随机共振(NO-SR)的信号误码率始终高于10-1。随机共振检测可有效改善系统误码率特性,但随机共振最佳系统参数随输入信噪比改变而改变,导致恒参随机过程检测性能较差。自适应随机共振检测能够根据整个系统的检测性能进行动态参数调整,可使系统达到最优的参数匹配效果,可明显改善系统误码率。ACA-ASR 虽然也可实现弱光信号的检测,但易发生系统参数陷入局部最优的问题。 当输入信噪比SNRin处于-15 dB~-5 dB 时,CFACA-ASR 检测性能明显优于ACA-ASR。
为了进一步说明所提算法的性能下限,分别仿真了不同采样率下通信系统的误码率,每个码元的采样点数分别设置为10、30、50、70、100 和150。现统计了信噪比为-10 dB 至0 dB 之间的误码率。如图11 所示为CFACA-ASR 算法在不同采样点数下的检测结果,其中虚线即FEC 的限值3.8×10-3。由于随机共振自身的检测机理以及改进蚁群算法对SR 系统参数的优化,CFACA-ASR 在信噪比为零以下时依然具有较好的检测性能。根据检测结果可知:信噪比一定时,随着采样点数的增加,系统误码率呈逐渐减小的趋势,当信噪比为-5 dB,采样点数为10 对应的误码率为0.070 7,采样点数为100 对应的误码率为7.33×10-6。
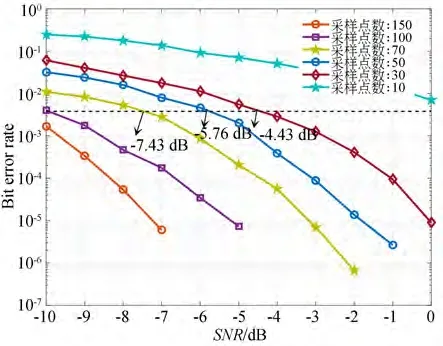
图11 CFACA-ASR 在不同采样点数下的误码率Fig.11 CFACA-ASR error rate under different sampling points
将CFACA-ASR 算法用于实时在线自适应处理时,可考虑引入训练序列。假设传输总码元个数为n个,现选取其中一部分码元作为训练序列,其余作为信息序列。根据训练序列进行自适应随机共振得到最优的系统参数,进一步使用最优参数处理信息序列。现选取了不同的训练序列分别进行参数自适应,总仿真码元个数为106个,分别仿真分析了训练序列码元个数为10、20和30 时对应的系统误码率,如表1 所示。对表中的数据分析可知,当训练序列的码元个数为10 个时,自适应匹配得到的随机共振参数就可进一步处理信息序列,且算法的数据开销约为10-5。

表1 不同训练序列长度在不同信噪比下的误码率比较Tab.1 Bit error rate comparison of different training sequence lengths under different SNR
5 实验分析
5.1 实验装置
水下无线光通信实验系统如图12 所示,发射端采用波长为520 nm 的激光二极管(Laser Diode,LD),且发射光功率为2.5 mW,利用任意波形发生器(RIGOL DG5352)产生信号并驱动LD。经过准直透镜后,从LD 发出的绿光经过一个长度为3 m 的水箱传输,且使用的水质为自来水,经实际测量,该水质的衰减系数c约为0.229 m-1。光束到达接收端后,透射光束通过透镜进行聚焦,并使用一系列透过率为20%、10%、1%、0.1%和0.01%的中性密度衰减片对接收光进行衰减。 接收端使用THORLAB 公司的APD430A2(M=100)光电探测器,调整镜头使光束全部聚集在APD 的探测面上,使用JYPXIE69852 数据采集卡(Data Acquisition Card,DAQ)获得输出脉冲,并在PC 中通过MATLAB程序进行离线处理。实验中使用3 m 水箱及衰减片模拟长距离水下信道对LD 光功率的衰减。

图12 UOWC 实验系统Fig.12 UOWC experimental system
5.2 实验结果
在实验系统中,噪声主要为探测器APD 自身的噪声,APD 的噪声主要分为两种:散弹噪声和热噪声。热噪声来源于器件内部载流子热运动,散弹噪声是由于光电效应产生的光生载流子随机起伏导致的,包括暗电流噪声、倍增噪声等,通过实际测量,实验系统中的噪声平均功率为0.42 μW。
由于水质对信号的衰减较大,因此影响水下光信号信噪比的因素主要为到达接收机的光信号功率,文中的信噪比是根据信噪比公式SNR=10lg(PsPn)计算所得,其中Ps是信号功率,Pn是噪声功率。发射端发送全“1”信号,接收端使用数据采集卡采集长度为N1的信号S1。发射端发送全“0”信号,接收端使用数据采集卡采集长度为N0的信号S0。对于实际采集的信号S0和S1,利用式(14)~式(16)即可求出接收信号的信噪比。
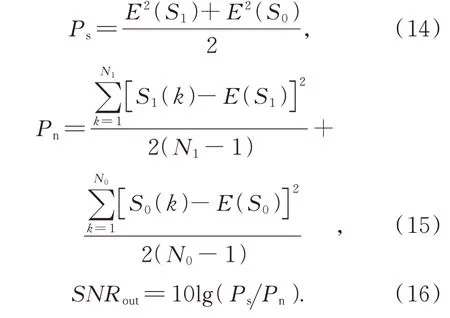
在实验中,利用任意波形发生器(RIGOL DG5352)产生占空比为50%的方波信号并驱动LD 光源,码元传输速率为1 MHz,每个码元的采样点数为100 个,蚁群算法所选参数与仿真参数相同,图13 为使用CFACA 算法完成参数a,b的最优值寻找并处理实验数据的结果,接收信号的信噪比为-4.559 5 dB,且CFACA 算法寻优结果为a=0.02,b=1.820 5,通过计算,使用CFACA-ASR 检测算法后信号的信噪比为2.643 7 dB,误码率为5×10-4。

图13 基于CFACA-ASR 系统处理的实验采集数据(SNR=-4.559 5 dB)Fig.13 Experimental data collected based on CFACAASR system processing(SNR=-4.559 5 dB)
图14 所示为不同检测方案下的接收信号信噪比与误码率的关系曲线图。实验结果表明,误码率与信噪比的变化趋势与仿真结果一致,但当信噪比一定时,实验误码率与仿真结果存在一定的差异。这主要是因为探测器噪声不是理想的高斯白噪声,导致实验结果与仿真结果存在差异。可以看出,使用随机共振系统对接收信号进行处理后,接收机的误码率性能有较大提升。对比不同的检测算法,可得出基于CFACA 的自适应随机共振检测方案性能最优。

图14 不同检测方案的实验结果Fig.14 Experimental results of different detection schemes
6 结 论
针对水下无线光通信接收信号低信噪比问题,提出了一种基于自适应随机共振的水下弱光信号检测方法,采用基于拥挤度因子的改进蚁群算法对随机共振的系统参数进行优化,将输出信号信噪比作为目标函数,动态调整系统参数,实现了随机共振最佳系统参数的自适应估计,仿真结果表明,相比恒参随机共振,所提出的检测方法在误码率方面有明显提升。搭建了UOWC 实验系统,实验结果表明,在接收信号信噪比为-4.559 5 dB 时,本文所提出的自适应随机共振检测方法的系统误码率为5×10-4,验证了该方法在水下无线光通信系统中的有效性。
