导弹伺服振动亚临界试验及稳定边界预示方法

高 阳，史晓鸣，张宏程，江玉刚，涂 静，赵 征

（1.上海机电工程研究所，上海 201109； 2.上海航天技术研究院，上海 201109）

现代导弹日益增大的机动过载及轻量化设计要求使得弹上稳定控制回路权限逐渐放宽、弹体结构模态频率不断降低[1]，伺服控制与结构振动耦合导致的大幅伺服（弹性）振动问题日益突出。吴云洁等[2]将导弹的弹性振动信号视作刚体运动信号的噪声进行自适应滤波处理。楚龙飞等[3]针对导弹1 阶模态频率的时变性提出自适应结构滤波器设计方法，用Nyquist 稳定性判据分析了系统的幅值裕度和相位裕度。张陈安等[4]在状态空间内耦合时域气动力、结构状态方程与控制状态方程，通过根轨迹法判别耦合系统稳定性。杨炳渊等[5]基于状态空间法建立导弹的模态状态方程和控制状态方程，在时域内用龙格-库塔法实现系统动力学响应的数值仿真，并借以判断系统的动力学稳定性，辨识稳定性的临界参数。许龙等[6]和李越群等[7]分别对导弹的俯仰/偏航通道和滚转通道的振动抑制和稳定回路设计进行了频域仿真分析，并提出抑制导弹伺服振动的改进措施。

上述研究均是针对简化后的结构/控制模型开展的数值仿真工作，实际工程型号的伺服振动模型更为复杂，且还存在间隙、摩擦等结构非线性以及舵偏指令限幅等控制非线性因素，导致数值仿真的结果并不能充分反映真实的情况，因此工程研制流程中必须开展伺服振动地面试验以评估其稳定性。史晓鸣等[8]用激振器扫频激励闭环试验揭示了导弹伺服振动系统的振动响应现象。国内工程单位亦总结制定了中华人民共和国航天行业标准《防空导弹稳定控制系统弹性抑制全弹模态试验方法》[9]和中国航天科技集团公司标准《战术导弹伺服弹性试验设计规范》[10]为导弹伺服振动地面试验提供了参考与指导依据。但上述标准中的试验方法均采用施加外部扰动后检查导弹振动是否衰减的方法来定性地判断系统是否稳定。若要进一步定量获得发生伺服振动的临界增益值，就只有通过逐步提高控制系统的增益，直至进入施加外部扰动后弹体结构等幅振动的临界状态，此时的系统增益即为系统发生伺服振动的临界增益。然而在伺服振动临界、超临界状态下，结构振动幅度很大，弹上电流快速增大，极易导致弹体结构以及弹上电子元器件的损伤。如何在较为安全的亚临界试验数据中获得有效的系统响应数据，并从中外推预示出系统伺服振动稳定边界，是当前导弹伺服振动试验研究中亟须解决的问题。

伺服振动亚临界地面试验及稳定边界预示的方法目前尚未见到公开报道。伺服振动的本质是图1所示闭环反馈的自激振动，因此可以借鉴同样属于自激振动的颤振问题的亚临界试验及边界预示方法。稳定性外推工作[11-12]是基于试验手段解决颤振问题的重要途径，张伟伟等在综述文献[13]中全面详细地评述了颤振亚临界试验及稳定边界预示方法的研究进展，其中阻尼外推法、包线函数法，物理概念清晰，只需要从亚临界试验数据中识别出阻尼或衰减包线随增益变化的规律即可预示边界参数，是工程中常用的方法。

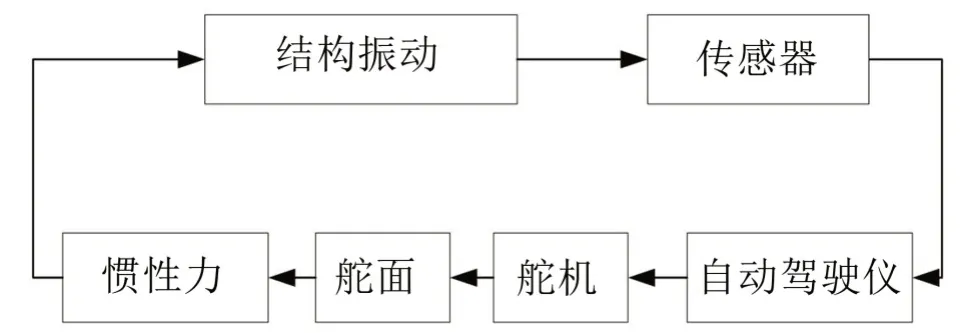
图1 伺服振动反馈回路

本文为解决当前工程中导弹伺服振动地面试验中存在的问题，提出导弹伺服振动亚临界地面试验及稳定边界预示方法。通过阶梯变增益的亚临界试验获取一系列不同驾驶仪增益条件下弹体结构振动响应信号；应用解析模态分解(Analytical Mode Decomposition，AMD)从弹体结构振动响应中提取出弹体结构的1 阶弹性响应，并用希尔伯特变换(Hilbert Transform，HT)实现伺服振动系统的非参数辨识；根据伺服振动系统阻尼比和振动信号包线函数形状参数随增益变化的规律外推预示伺服振动稳定边界。试验及预示结果表明，本文方法只需要开展若干次亚临界试验，即可通过对亚临界状态下的系统振动响应数据处理，有效准确地预测出导弹伺服振动系统的稳定边界，具有良好的工程适用性。

1 基本理论

1.1 解析模态分解

解析模态分解[14]的本质是一个自适应带通滤波器。解析模态分解能分解紧密间隔频率成分的信号，应用的前提条件在于确定带通频率范围，适用于已知谐振频率的伺服振动系统本征模态信号提取。

对于一个实信号q(t)，设它包含n个频率成分ω1，ω2，…，ωn的单频率信号，一个频率ωi对应一个单频率信号qi(t)，所以：

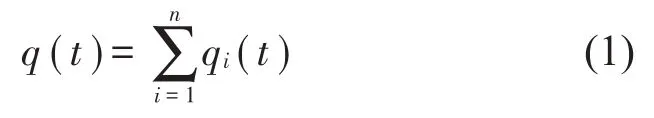
那么存在n-1 个二分频率ωbi∈(ωi,ωi+1), i=(1,2,…,n-1 )，将q(t)分为高低频的两个部分

其中：

式中：si(t)为频率小于ωbi的低通信号t)为频率高于ωbi的高通信号。符号H[·]表示希尔伯特变换。

因此，单频率成分信号可以表示为：

1.2 希尔伯特变换[15]求包络线

定义解析信号Q(t)由原始信号q(t)及其希尔伯特变换构成：

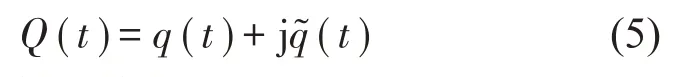
写成幅值/相位形式：

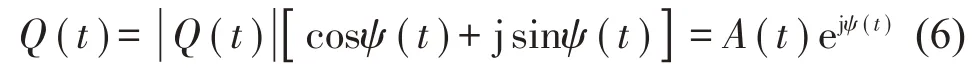
式中：A(t)为瞬态振幅，同时表征原始信号q(t)的包络线；ψ(t)为瞬态相位：

1.3 边界预示方法

1.3.1 阻尼外推法

阻尼外推法以模态阻尼作为自激振动是否发生的稳定性判据。理想单自由度系统的自由振动衰减信号具有如下形式：

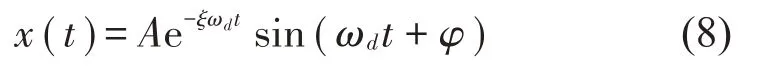
式中：ξ表示阻尼比，ωd表示振动圆频率，φ表示初始相位。由式(7)可知，该信号的包络线（瞬态振幅）为：

由于结构非线性、控制非线性尤其是舵系统非线性的存在，试验实测信号并不是理想单频信号，解析模态分解后的信号仍然在模态频率附近出现图2所示的超谐波现象，时间历程呈现“拍”的形式。针对这种现象，采用局部极值插值法[16](Local Maxima Interpolation，LMI)提取该信号包络线的驻点dA/dt=0做指数函数拟合得到图3中包络线的包络线(Envelope of Envelope，EOE)，根据EOE 的指数项系数-ξωd辨识伺服振动系统阻尼比。

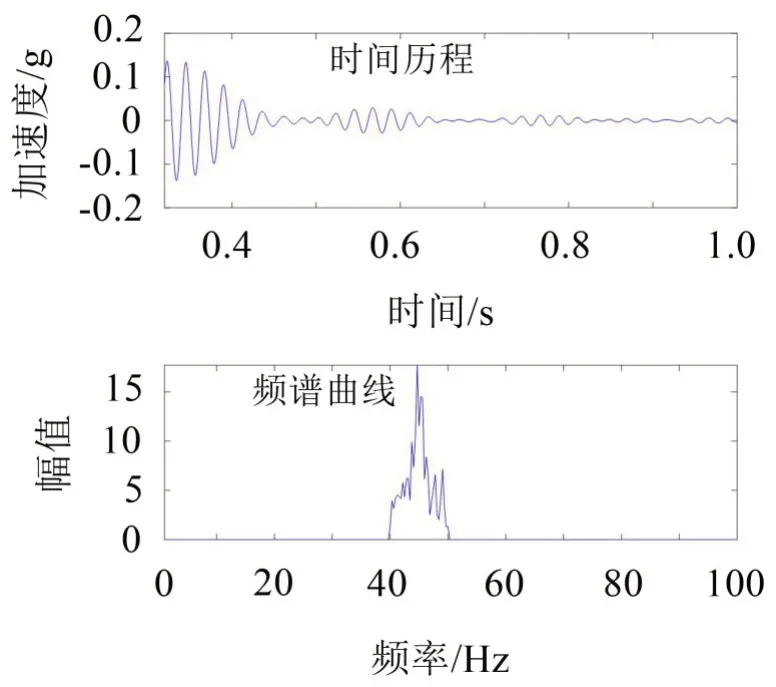
图2 实测信号的解析模态分解

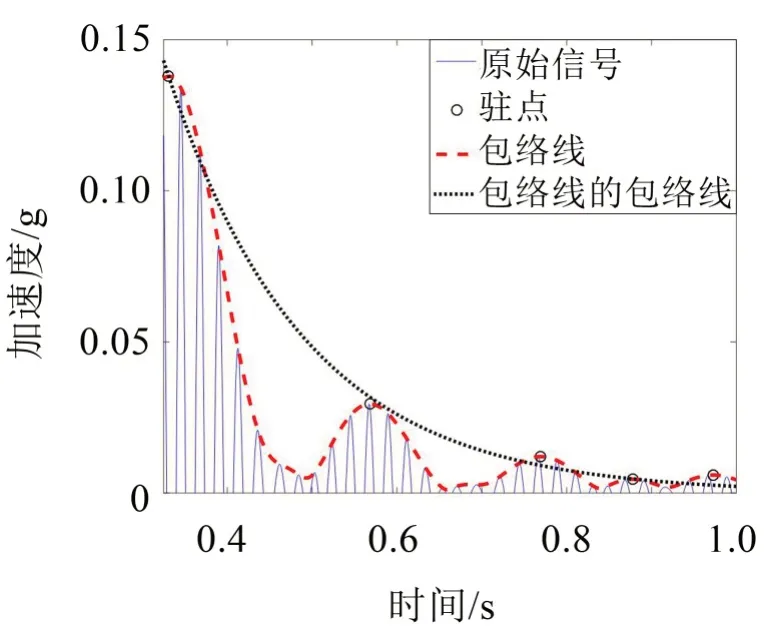
图3 原始信号、驻点、包络线及包络线的包络线

1.3.2 包线函数法

包线函数法不需要识别系统模态参数，直接用振动响应包络线（包线函数）的形状参数S表征系统阻尼大小。形状参数的定义是包络线在时间轴上形心位置的倒数S=对于单频信号，现在普遍采用希尔伯特变换构造包络线A(t)=± ||Q(t)=±对应的形状参数表达式为：

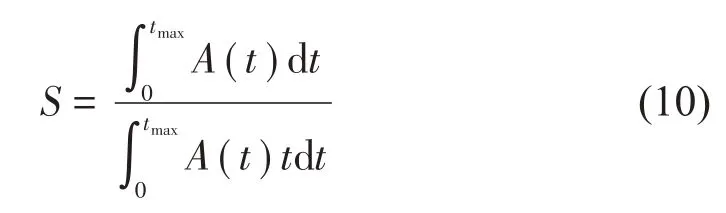
式中：tmax为选取的所围面积对应的最大时间，由信号品质和振动衰减快慢决定。

理论上，形状参数的取值范围为[ 1/tmax,∞]。形状参数S的减小意味着阻尼的降低。S＞2/tmax时，响应衰减，系统稳定；S=2/tmax时，响应等幅振荡，系统临界稳定；S＜2/tmax时，响应发散，系统不稳定。

2 伺服振动亚临界试验方法

本文提出的伺服振动亚临界试验方法用地面综测设备给驾驶仪装定固定弹道点控制参数并给惯导、驾驶仪、舵机等弹上设备供电，用锤击脉冲激励弹体结构振动，用加速度传感器采集弹体振动响应，试验系统布置见图4。脉冲激励下，模态坐标上伺服振动系统自由振动方程具有如下形式：

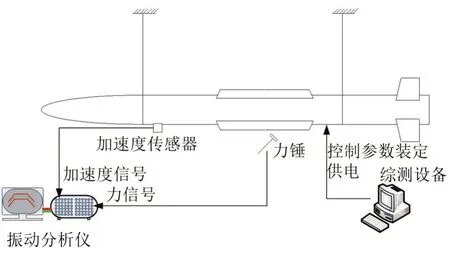
图4 试验系统

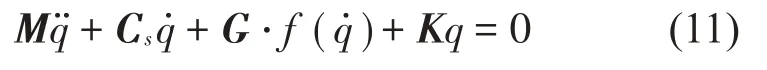
式中：q表示模态坐标，M、Cs、K分别为弹体结构模态质量、模态阻尼和模态刚度，f(q)表示控制系统对弹体的非线性作用力，G为驾驶仪控制增益。由于实际弹体结构模态阻尼Cs较小可忽略不计，式(11)可改写为：

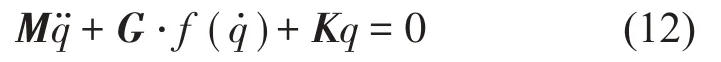
在亚临界状态下，脉冲激励后伺服振动系统处于自由衰减振动过程。系统振动衰减快慢主要取决于等效阻尼力G·f中控制增益G，不同的控制增益对应不同的伺服振动系统阻尼。通过阶梯变增益的亚临界试验获取一系列不同驾驶仪增益条件下弹体结构振动响应信号，辨识亚临界状态下的系统阻尼并外推预示使系统阻尼为零的临界控制增益。

结合亚临界试验方法与数据处理方法总结伺服振动亚临界试验及边界预示方法的步骤为：

(1)用地面综测设备给驾驶仪装定固定弹道点控制参数，并给惯导、驾驶仪、舵机等弹上设备供电；

(2)对弹体施加脉冲激励，利用加速度传感器采集导弹弹体结构的脉冲响应信号；

(3)断电，在亚临界状态下阶梯增大装定驾驶仪的控制增益，然后重复上述步骤(1)至步骤(3)开展若干组亚临界状态下的试验；

(4)滤除所采集振动信号中的低频刚体运动信号和高频噪声；

(5)对滤波后的信号在所关心的系统1 阶谐振频率附近设置合适的频带区间做解析模态分解；

(6)对解析模态分解后的信号进行希尔伯特变换，得到瞬态幅值（包络线）；

(7)基于阻尼外推法或包线函数法辨识每个控制增益条件下的系统阻尼；

(8)根据多组控制增益-系统阻尼的对应关系，外推预示使系统阻尼为零的临界控制增益。

图5 给出了上述亚临界试验及边界预示流程图。

图5 亚临界试验及边界预示流程

3 试验算例

为验证本文提出的伺服振动亚临界试验及边界预示方法的有效性，对控制系统装定固定弹道点参数状态下的导弹全弹开展了伺服振动试验。选取控制增益放大倍数K=1、5、10、15 共四个亚临界试验状态。

试验中脉冲激励输入由人工力锤敲击给出，振动响应由加速度传感器采集。加速度传感器位于导弹惯导处，力锤激励点位于靠近惯导的弹身中部。力锤采用B&K8206型力传感器，加速度传感器采用PCB333B30 型加速度传感器用于采集加速度与力信号，采样频率2.56 kHz，采样时间3.2 s。采用触发方式，以力锤敲击时间作为采集起点，并在触发前预采集10%时间（即0.32 s）确保响应信号经数据处理后的完整性。由于试验状态较多，本文选取K=1 原始控制增益对应的振动响应为例介绍数据处理过程。

首先对原始振动响应做15 Hz～100 Hz 带通滤波，再将滤波后的信号做50 Hz～60 Hz 解析模态分解，图6 给出解析模态分解后信号的时间历程以及频谱图，可以看出频带内存在一明显谐振峰值；继续对该信号做希尔伯特变换，得到图7所示的包络线；归一化包络线的时间长度，并拟合出图8 所示EOE曲线。根据阻尼外推法，利用EOE曲线的指数项系数-ξωd求出阻尼比ξ=1.97%；根据包线函数法，利用包络线计算出形状参数S=6.075。

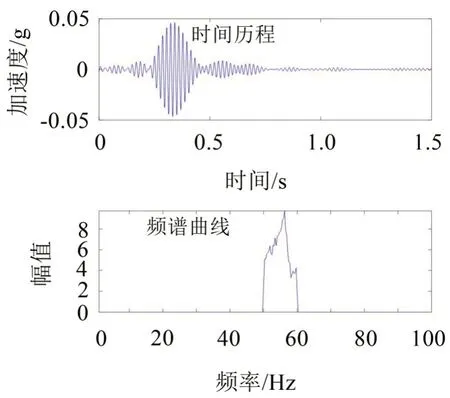
图6 解析模态分解结果

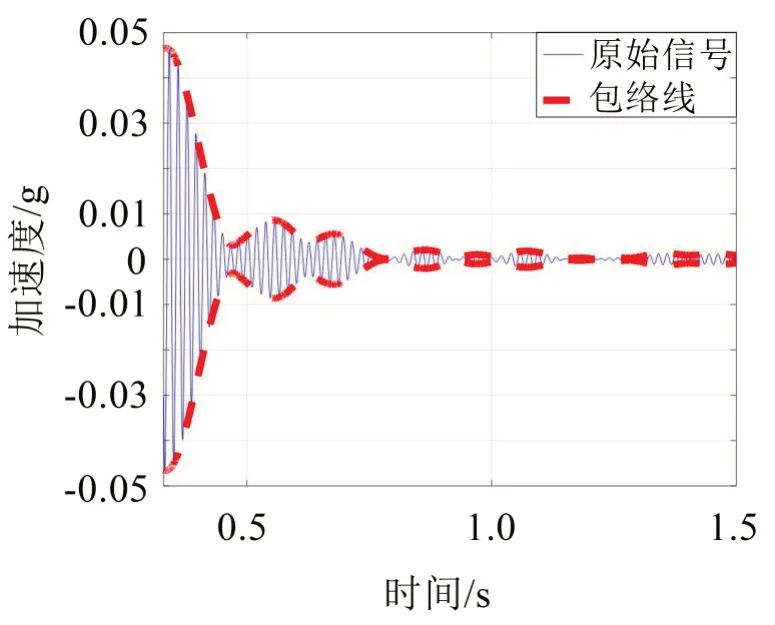
图7 振动响应包络线

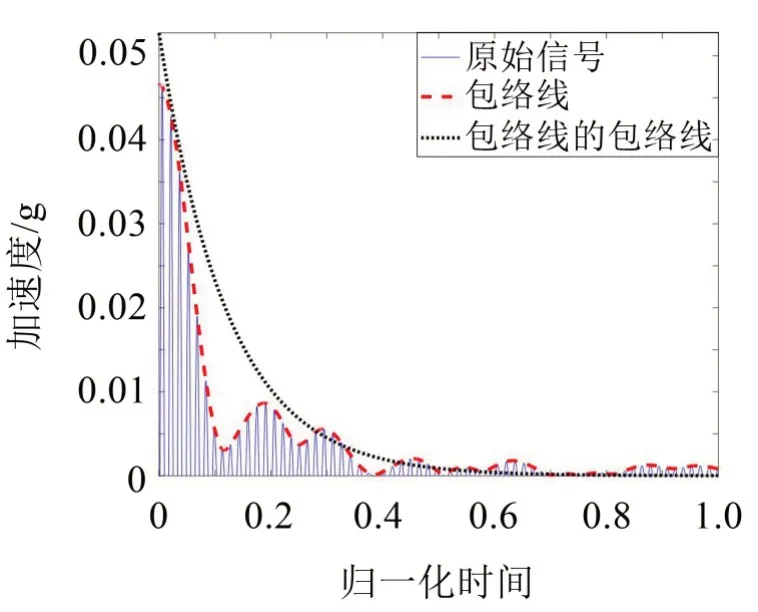
图8 振动响应包络线的包络线

对控制增益放大倍数K=5、10、15条件下的振动响应重复上述步骤，最终得到表1 所示阶梯改变的控制增益与两个稳定性判据之间的对应关系。

表1 控制增益放大倍数与稳定性判据的对应关系

基于最小二乘原理对控制增益放大倍数与稳定性判据的对应关系做拟合，外推出临界稳定性判据对应的控制增益放大倍数。临界阻尼比ξ=0，临界形状参数S=2/tmax=2，图9和10分别给出阻尼外推法和包线函数法拟合的外推曲线与临界控制增益放大倍数。

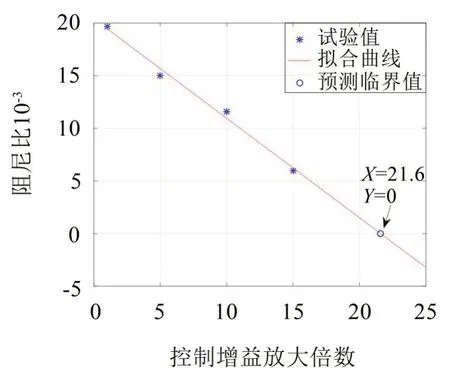
图9 阻尼外推法结果

图10 包线函数法结果

阻尼外推法得到的临界控制增益放大倍数K=21.6，包线函数法得到的临界控制增益放大倍数K=19.0。两种预示方法得到的临界控制增益放大倍数K≈20，继续阶梯增加控制增益令放大倍数K=20以验证预示结果，得到的原始振动响应信号如图11所示。此时振动响应已经呈现明显的不收敛等幅振荡趋势，已达到临界失稳状态，证明K=20 十分接近临界稳定放大倍数，也验证了两种预示方法的正确性。

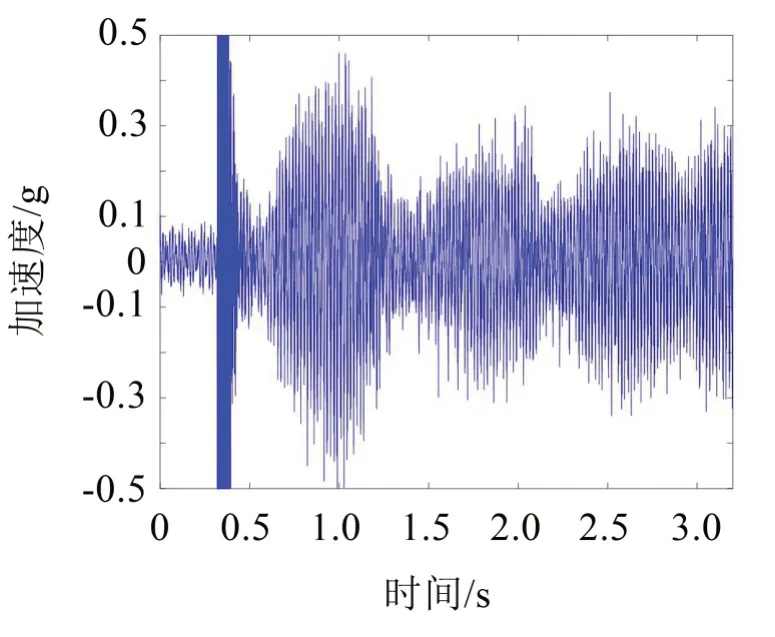
图11 20倍控制增益下振动响应

4 结语

(1)设计了阶梯变增益的导弹伺服振动亚临界试验方法：阶梯改变驾驶仪控制增益放大倍数，获取不同控制增益下弹体结构脉冲响应衰减的变化规律。基于不同的控制增益条件，该亚临界试验方法采集的振动响应可表征伺服振动系统的动力学特性，为辨识伺服振动动力学系统提供输入。

(2)提出了导弹伺服振动动力学系统辨识及亚临界试验稳定边界预示新方法：以阶梯变增益的亚临界试验中不同控制增益下弹体结构振动响应作为输入，基于解析模态分解及希尔伯特变换方法辨识伺服振动系统动力学参数，根据伺服振动系统阻尼比和振动信号包线函数形状参数随增益变化的规律外推预示伺服振动稳定边界，实现伺服振动系统的稳定边界预示。

(3)亚临界预示试验结果与临界试验结果的一致性表明，本文提出的伺服振动亚临界试验及稳定边界预示方法能有效评估导弹伺服振动系统的稳定边界，为导弹伺服振动控制设计与评估创新性地提供了一种可信、有效的验证手段。