半主动悬架SH-LQR阻尼控制策略仿真研究
2022-07-04刘夫云邓聚才赵亮亮唐振天
王 越,刘夫云,邓聚才,赵亮亮,唐振天
(1.桂林电子科技大学 机电工程学院,广西 桂林 541004;(2.东风柳州汽车有限公司 商用车技术中心,广西 柳州 545005)
近年来,半主动悬架逐渐成为车辆悬架系统的热门选择。传统的被动悬架往往只能在特定的工况下表现出良好的减振效果,而半主动悬架实现了阻尼的可调,能在大多数工况下表现出较好的性能。同时,半主动悬架能实现大部分主动悬架实现的效果,且半主动悬架耗能较小,可靠度高[1]。因为其减振效果好,成本较低的优点,半主动悬架在各类车型上被大量应用。半主动悬架通过改变阻尼来实现更好的控制效果,因此,半主动悬架控制算法的研究是实现其功能的重要一环。
自20世纪90年代以来,半主动悬架的设计制造及控制算法的开发应用逐渐成为领域内的热点。相关控制算法的研究更是其中重点。较为经典半主动悬架控制算法有天棚阻尼(Skyhook,SH)控制、地棚阻尼(Groundhook,GH)控制、加速度阻尼(Acceleration Driven Damping,ADD)控制等,这一类的控制方法往往基于特定的理想化假设,控制目标单一,控制适用的工况也有一定的局限性,如天棚阻尼控制适用于低频段,在高频时反而会产生恶化的效果,加速度阻尼控制在高频段效果较好,低频段效果不如被动悬架。也有以传统控制理论作为基础的PID(Proportional Integral Derivative)控制、LQR(Linear Quadratic Regulator)控制、滑模控制[2-3]等控制算法。近年来,逐渐出现了基于现代控制方法的模型预测控制(Model Predictive Control,MPC),模糊控制算法[4],使用粒子群算法、神经网络优化的控制算法[5]等半主动悬架控制方法,此类方法控制效果较好,但算法结构复杂,实际应用时计算量大,成本较高[6]。各控制方法都具有其优势和劣势,因此,结合不同的控制算法,实现优势互补是半主动悬架控制算法发展的一个趋势。郭孔辉等[7-8]提出了一种改进的加速度阻尼控制方法,结合了天棚控制和加速度阻尼控制,在全频段都拥有较好的控制效果。单一的控制算法一般有其局限性,往往在某一工况下效果较好,其他工况控制效果不好,甚至导致结果的恶化,难以满足多工况下的控制需求。因此,通过分频的方式先区分高低频,再结合不同控制算法适用的频段,能实现全频段的有效控制,解决单一算法的不足之处。
基于以上单一控制方法存在的局限性和解决思路,本文首先分析开关天棚控制和LQR 控制,开关天棚控制在低频时有较好的控制效果,LQR 控制在高频时有较好的效果,结合两者的优点,通过分频的方式,实现一种改进的LQR 控制,使其在全频段都拥有较好的控制效果。而后提出一种将该控制方法从1/4车辆模型移植到半车模型的方案,通过仿真验证其效果。
1 SH和LQR介绍分析
图1 所示为1/4 车辆动力学模型,它结构简单,具有两自由度,能反映垂向的振动,常被用于半主动悬架控制算法的初期验证,对其进行动力学建模如下:
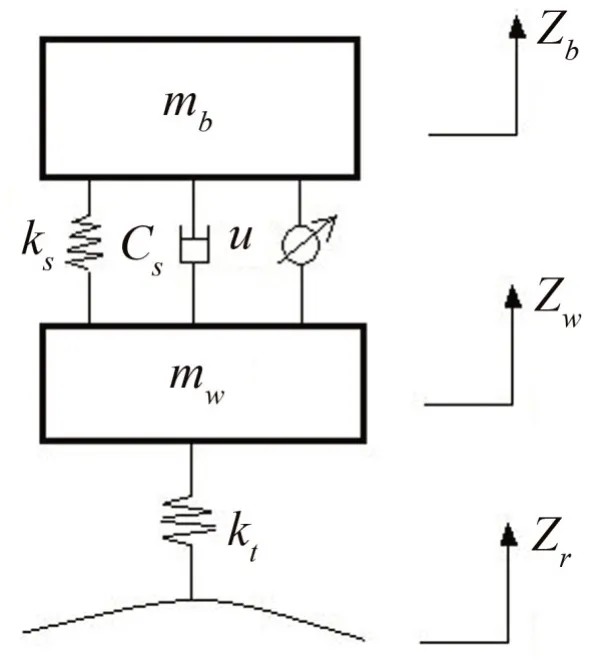
图1 1/4车辆动力学模型
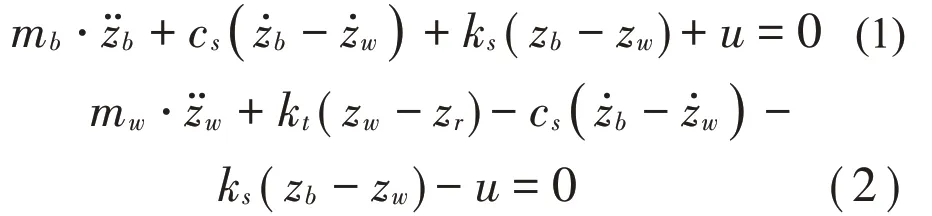
式中:mb为簧上质量;mw为簧下质量;cs为被动悬架的阻尼系数;ks为减振器的刚度系数;kt为轮胎的刚度系数;u为可调阻尼输出的阻尼力,在模型中替代半主动悬架的阻尼力;zb,zw,zr分别为簧上质量,簧下质量和路面的垂向位移。
1.1 SH控制分析
天棚阻尼(SH)控制是经典的半主动悬架控制方法,其核心思想为:假设簧上质量与固定的参考位置(天棚)之间连接有阻尼器,从而抑制簧上质量的振动,达成控制目的。在实际情况中,“天棚”并不存在,因此实际控制中,都是用其他的方法来模拟理想天棚阻尼控制的效果,最简单的开关天棚控制思路如下:
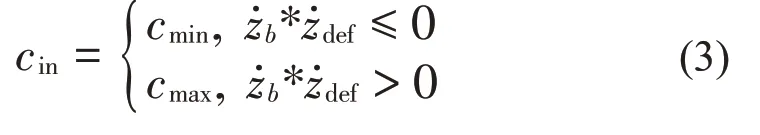
式中:cin为半主动悬架提供的阻尼;cmin和cmax分别为可控阻尼器可调的最小和最大阻尼;zdef为悬架相对运动速度。
1.2 LQR控制分析
LQR(Linear Quadratic Regulator)是线性二次型调节器的简称,线性二次型问题的最优解可由统一的解析式求得,得出相应的状态反馈控制,构成闭环的线性最优控制,具有实现简单,控制效果优秀的特点,在实际工程问题中也得到了应用。
将LQR应用到半主动悬架的控制时,根据半主动悬架系统的特性,选择使用无限时间定常状态调节器,其最优状态反馈矩阵可以通过离线计算得出,计算量小,更加适合应用于工程实际。
图1中所示的车辆动力学模型可以用状态空间方程表示如下:

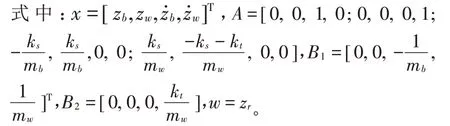
性能指标为:

式中:Q为半正定对角矩阵;R为正定对角矩阵。两者分别用于控制系统在调节过程中的动态跟踪误差和消耗的控制能量。
根据控制目标选取较优的Q,R取值,由里卡蒂方程求得反馈矩阵,得出系统的反馈输入为:
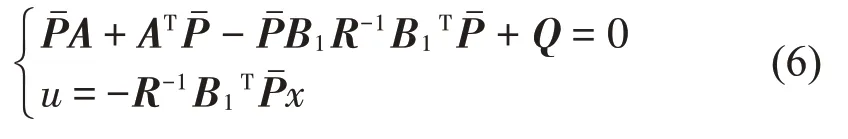
1.3 SH和LQR控制仿真分析
在Simulink中建立1/4车辆动力学模型,通过仿真对比验证被动悬架,SH 控制和LQR 控制的减振效果,模型的参数如表1。

表1 1/4车辆动力学模型参数
以正弦波扫频作为路面输入,仿真验证各控制方法从路面输入到簧上质量振动加速度的幅频特性,结果如图2 所示。从中可以看出,在频率较低时,开关天棚的减振性能优于被动悬架,在高频时会恶化。LQR控制在高频时有较好的减振效果。
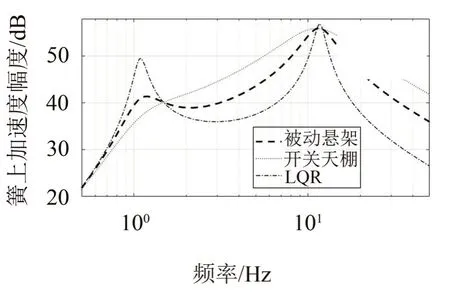
图2 路面输入到簧上质量加速度的频率响应
2 改进的SH—LQR
由上文幅频特性的仿真结果可以看出,天棚控制算法在低频具有较优的控制效果,LQR 在高频段具有较优的控制效果。因此,寻找一种分频的方法,从而实现SH-LQR 联合控制,在低频和高频都能有较优的控制效果。
2.1 SH-LQR控制规律的提出
首先从能量流动的角度对1/4 车辆动力学模型和天棚阻尼控制算法进行分析,如图1所示的模型,模型的总动能为簧上质量的动能和簧下质量的动能之和:
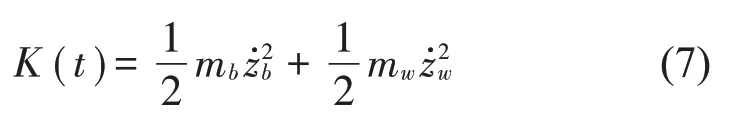
模型的总弹性势能为车轮中的弹性势能和减振器弹簧中的弹性势能之和:
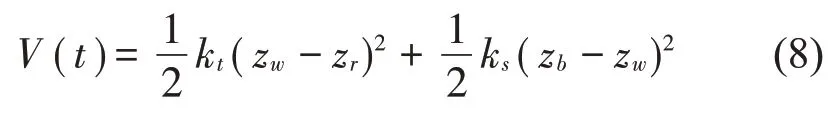
在整个模型中,只有减振器阻尼消耗能量,减振器阻尼吸收簧上质量能量的功率为:
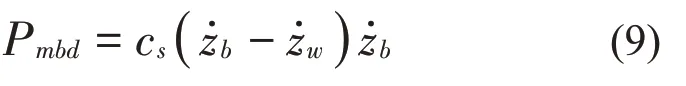
减振器阻尼释放能量给簧下质量的功率为:
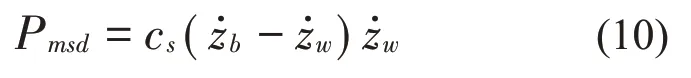
观察开关天棚阻尼控制的切换规则,当减振器阻尼吸收簧上质量的能量时,阻尼被调到最大,当减振器阻尼向簧上质量释放能量时,阻尼被调到最小。因此,开关天棚控制的思想在能量流动中可以被解释为:尽可能使用减振器阻尼消耗簧上质量的能量,实现减振效果。
当Pmbd+Pmsd≥0 时,减振器吸收簧上质量能量的能力更强,悬架能够将簧上质量吸收的所有能量转移到簧下,此时使用开关天棚阻尼控制的效果更好。当Pmbd+Pmsd<0 时,使用LQR 的控制算法能实现更好的控制效果,由上面的分析可得,Pmbd+Pmsd的正负等价于的正负,因此得出控制规律如下:

在仿真中验证该控制方法的分频效果,设置输入为扫频输入,仿真结果如图3 所示,可以看出,在低频时,在高频时相反,说明了分频方法的有效性。
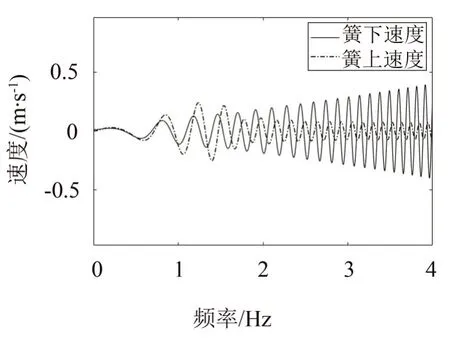
图3 扫频输入时簧上速度与簧下速度对比
同样使用前文建立的1/4车辆动力学模型,正弦扫频信号输入得出各控制算法的频响曲线见图4,可以看出,SH-LQR 控制算法在低频段的效果与开关天棚相似,在高频段和LQR 控制重合。因此,SHLQR在高频段和低频段都有较好的减振效果。
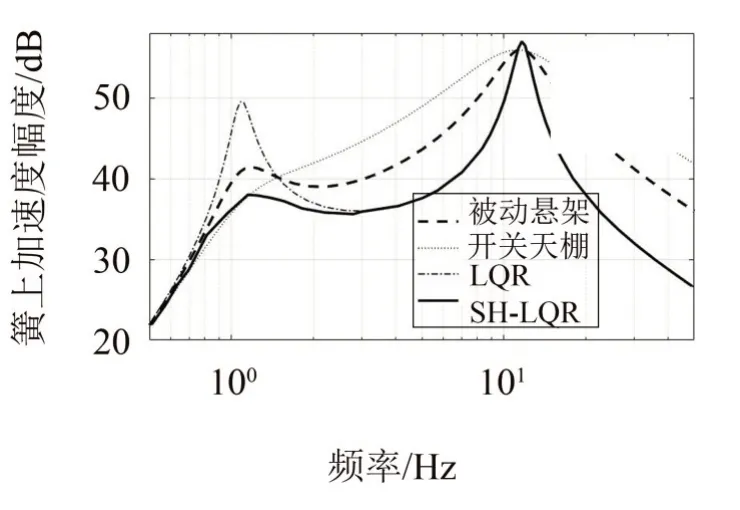
图4 各控制算法路面输入到簧上质量加速度频率响应
使用随机路面输入是半主动悬架仿真中的一种常用方法,建立随机路面的方法有白噪声法、傅里叶逆变换法、谐波叠加法等[9]。本文使用白噪声法建立随机路面输入,该方法实现简单,在低速时准确度较好,白噪声法的公式如下:
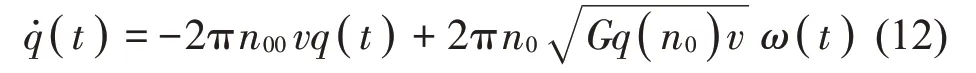
使用E级随机路面作为输入,车速为30 km/h进行仿真,截取了一段时间的加速度数据如图5所示,全程的加速度均方根值如表2所示,可以看出,和被动悬架以及开关天棚、LQR 控制下的半主动悬架相比,SH-LQR 对簧上质量振动加速度的优化效果更好。
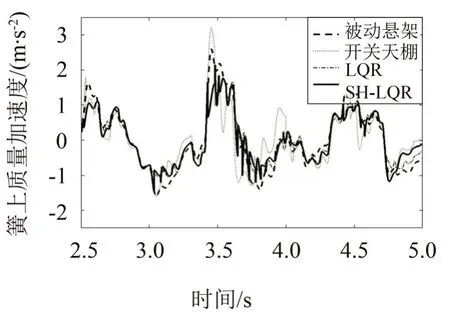
图5 随机输入时各控制算法控制下簧上质量加速度
表2 不同控制策略下均方根值对比

表2 不同控制策略下均方根值对比
?
2.2 SH-LQR控制在半车模型上的运用
相比于1/4车辆模型,半车模型增加了俯仰方向的运动,更贴近于实车行驶中的平顺性状况。且半车模型中存在运动方向的耦合,用于验证半主动悬架控制算法更加具有代表性。下面提出一种将SHLQR 算法移植到半车模型上的方法,并通过仿真验证其控制效果。
在SH-LQR算法中,首先需要通过的正负来确定使用SH控制算法或者LQR控制。当应用在半车中时,首先两个悬架分别判断应使用SH控制算法或LQR控制,若其中一个悬架或两个悬架都需要使用LQR控制时,将该悬架的输入作为状态空间方程的输入,使用LQR控制的方法进行控制。控制规则如下:
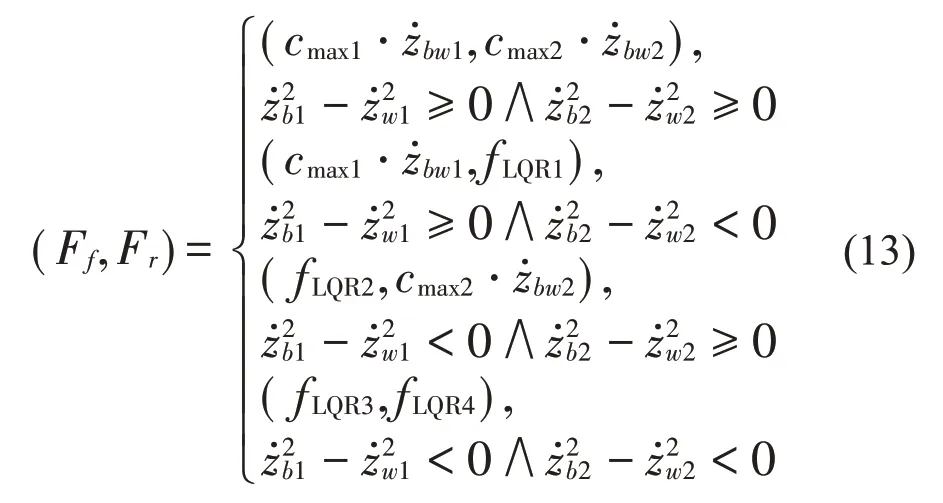
式中:Ff,Fr分别为前悬和后悬减振器可变阻尼的力;cmax1,cmax2分别为前后悬能调节的最大阻尼;分别为前悬和后悬上下端垂向运动的相对速度分别为前悬和后悬上端垂向运动的绝对速度分别为前悬和后悬下端垂向运动的绝对速度;fLQR1为只有前悬使用天棚阻尼控制时,由LQR控制计算出的后悬需要输入的阻尼力;fLQR2为只有前悬使用天棚阻尼控制时,由LQR控制计算出的前悬需要输入的阻尼力;fLQR3,fLQR4分别为前后悬都使用LQR控制时,计算得出的前后悬需要输入的阻尼力;
图6为4自由度半车的动力学模型,对其进行建模如下:
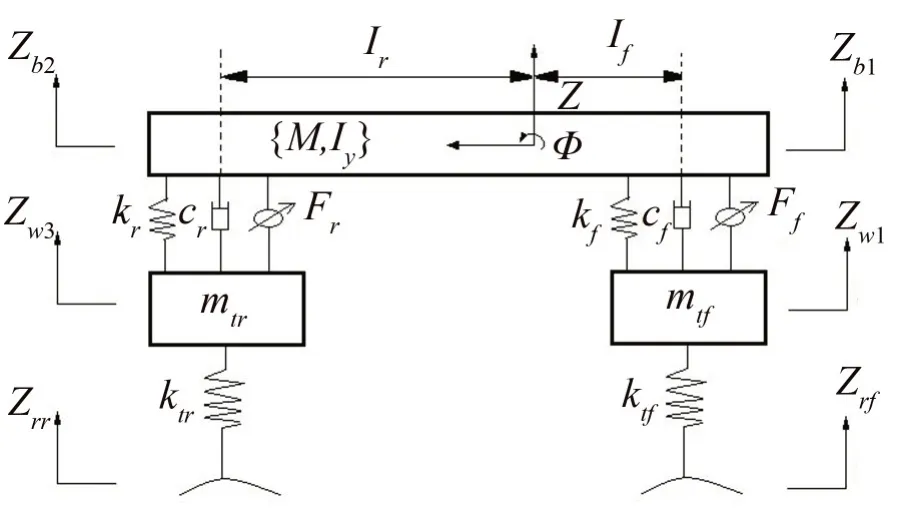
图6 半车动力学模型
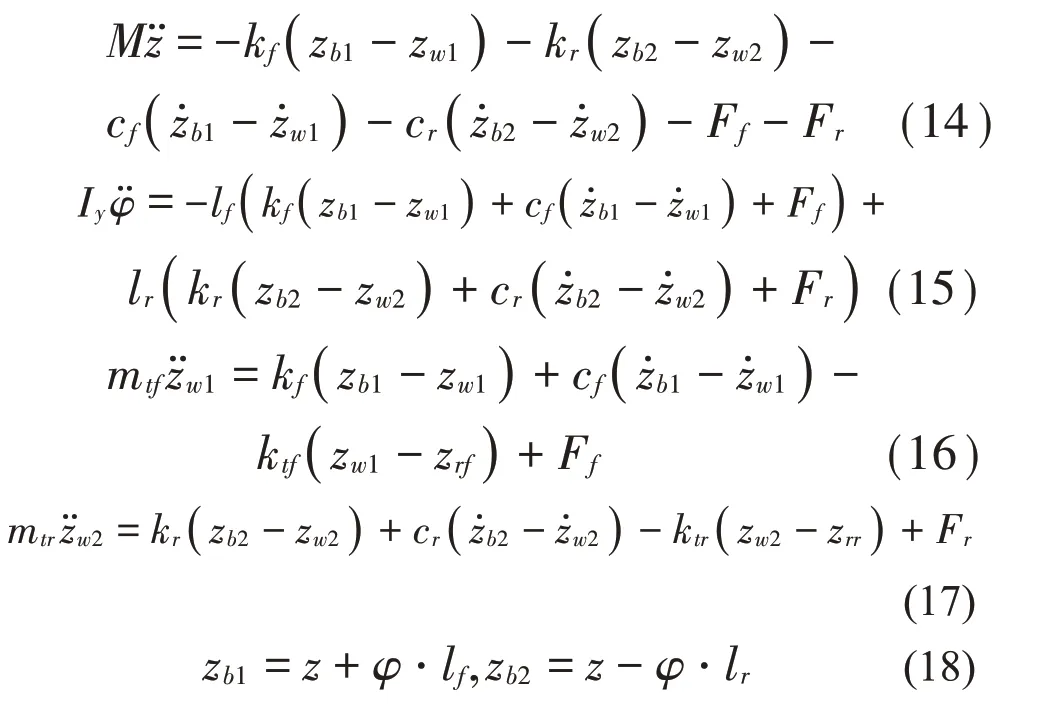
式中:M为折算到半车的车身质量;z,φ分别为车身垂向运动的位移和车身俯仰角;mtf,mtr分别为前后簧下质量;kf,kr分别为前后悬刚度;cf,cr分别为前后悬被动阻尼;ktf,ktr分别为前后轮胎刚度;lf,lr分别为前后悬架点到车身质心的距离;zrf,zrr分别为前后轮路面输入的位移。
3 仿真分析
半车动力学模型车辆参数如表3所示。
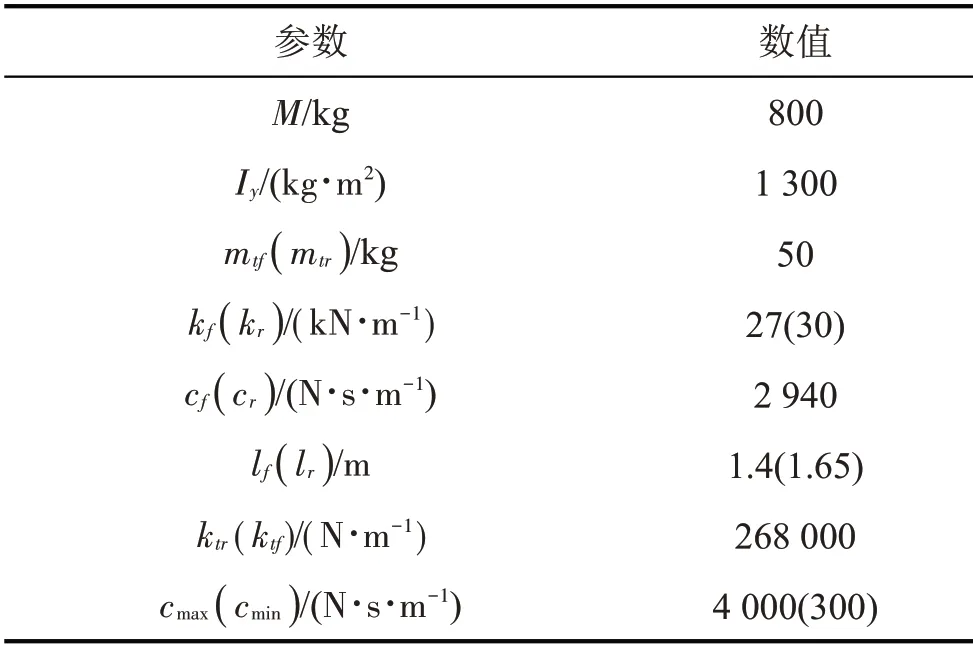
表3 半车动力学模型参数
在simulink 中建立仿真模型,使用上文白噪声法生成的E级路面作为输入,车速为30 km/h进行仿真,仿真总时间为50 s,对比被动悬架,LQR 控制,SH-LQR控制的效果见表4,截取一段时间如图7,图8所示,图9为全程车身质心加速度的频域对比。
表4 不同控制策略下均方根值对比

表4 不同控制策略下均方根值对比
?

图7 各控制算法下车身质心垂向加速度对比
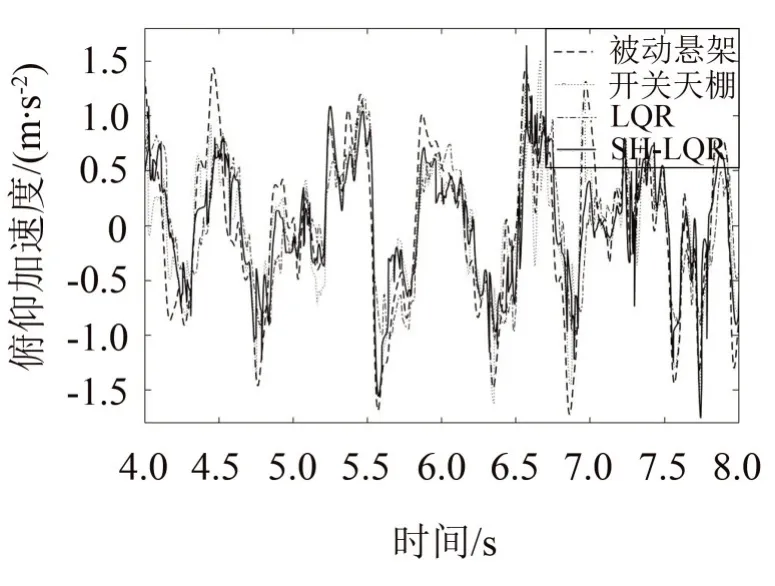
图8 各控制算法下车身质心俯仰加速度对比

图9 各控制算法车身质心垂向加速度频域对比
4 结语
本文首先分析了天棚阻尼算法和LQR 控制算法各自的控制特性,针对改善舒适性的目标,提出了一种SH-LQR联合控制的半主动悬架控制方法。并根据能量流动的分析选取了一种高低频分频方式,将其用于SH-LQR 联合控制的算法。首先在1/4 车辆模型上进行了仿真验证。结果表明,SH-LQR 控制算法在高频段和低频段都有较好的控制效果。而后建立了4自由度的半车模型,提出了将SH-LQR控制方法移植到半车的思路,并使用模拟的随机路面作为输入对控制算法的减振效果进行了仿真验证。仿真结果表明,SH-LQR 控制算法在改善舒适性方面有较好的效果。下一步将使用更多的工况对该算法进行仿真验证,如冲击路面等。同时,也将在台架试验与实车中对该算法的控制效果进行验证。
