海洋平台周期桁架结构振动特性研究

2022-07-04夏兆旺茅凯杰许祥曦

噪声与振动控制 2022年3期

夏兆旺，曹锐，茅凯杰，许祥曦

（1.江苏科技大学能源与动力学院，江苏镇江 212003；2.中国船舶集团第七一一研究所，上海 201108；3.江苏海事职业技术学院船舶与海洋工程学院，南京 211100；4.船舶与海洋工程动力系统国家工程实验室，上海 201108）

我国近年来对海洋资源发掘力度逐年加大，对海洋工程装备的技术要求也越来越高，海洋平台作为油气资源开发的基础设施，对其展开研究具有重要意义。海洋平台受到恶劣环境影响会产生结构振动，引起平台设备故障及人员的安全等[1]。在高盐度强紫外线海洋环境中，目前常采用的黏弹性阻尼减振措施的使用寿命有限，引入新的、有效的海洋平台减振措施具有重要的研究意义。

在周期结构中，弹性波传播的时候，会发生振动带隙的特性[2]，其机理主要有两种，分别为局域共振机理和布拉格散射机理[3]。其中，布拉格带隙产生的主要原因是在特定频段内周期结构中弹性波传播时会相互影响，无法产生与之相对应的振动模态，抑制弹性波传播[4-5]。因此，掌握周期结构带隙产生规律，达到对特定频段的振动控制对海洋平台的设计有重要意义。

本文主要研究周期导管的带隙及振动特性，将其应用到海洋平台的结构设计中，以提高海洋平台的稳定性和减振性能。通过有限元仿真的方法，建立周期导管及周期桁架结构的有限元模型，研究周期导管的晶格对带隙的影响规律，实现周期导管与传统桁架结构的结合，利用带隙特性控制振动波在海洋平台结构中的传递[6-7]。

1 周期结构振动求解理论

1.1 周期结构振动带隙的计算方法

将组成无限周期弹簧质量系统的晶格化简成s个弹簧和与其对应的振子串联的质量系统[8-10]。

其中晶格l 保持不变，振子间距为h，用以下方程表示单周期系统第t个振子动力学方程：

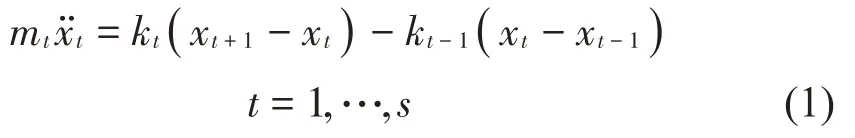
式中：xt是mt的位移。在周期边界条件下，方程（1）的解可写为：

式中：At为第t个振子的振幅，q为第t个振子的位相因子，ω为角频率，dt为第t和第t+1 个振子的间距；波矢q在第一布里渊区(-π/a,π/a)取值，其中a=

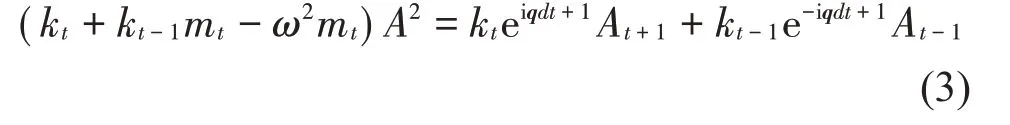
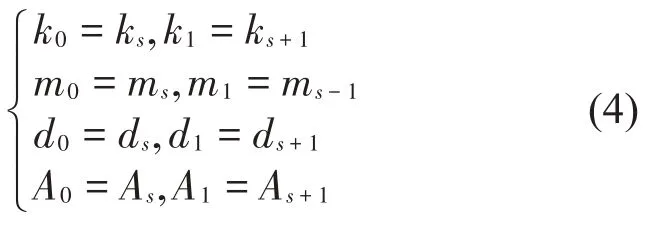
将式（4）代入式（3），该线性方程组可用矩阵形式表示为：

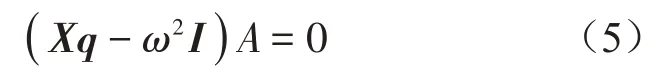
式中：I为n*n单位矩阵。A如果有非零解，则其系数行列式等于零，因此式（5）的求解就转变成求解n*n矩阵X的特征值问题。这样一维周期结构就可以推出带隙的起始频率和带宽，并可以推出截止频率。

1.2 导管结构振动响应计算方法

导管的轴向振动方程为：

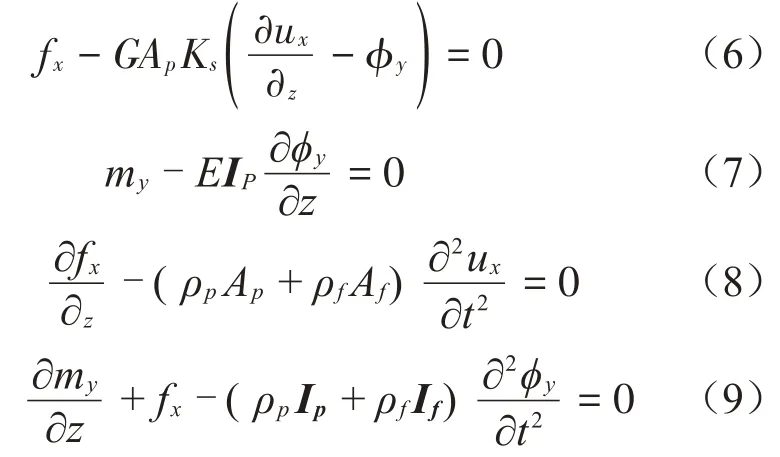
式中：fx，G，Ks，ux，my，ϕy分别为导管横截面沿x方向的剪切力、位移、转角和转矩；If和Ip分别为流体和管路的转动惯量；ρ为材料密度；Af为流体的横截面积。

导管径向的振动方程定义为：

式中：u代表x处的位移。

1.3 周期结构传递特性及减振性能评价方法

在有限周期结构中，带隙内弯曲振动波仍可传递，且表现为逐渐衰减形式。由于激励和响应幅值存在数量级的差异，通常采用如下传递函数定义，即插入损失：

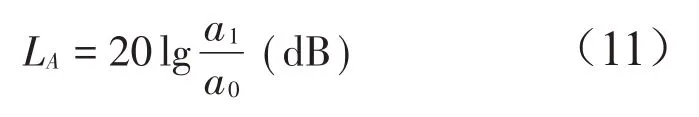
式中：LA为插入损失，a1为输入，a0为输出，本文为加速度响应，a0=10-6m/s2时的插入损失为该点振级。

通过计算总的振级差作为减振性能的评价方法，如下公式：

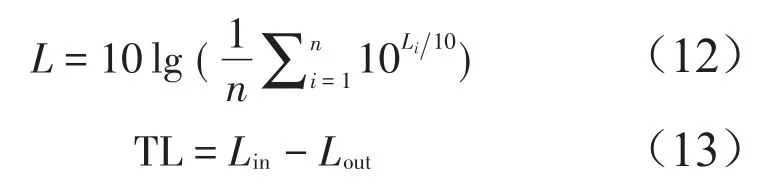
式中：Li为某一频点处振级，n为频率点总数，Lin为输入平均振级，Lout为输出平均振级，TL为平均振级的差，即减振性能。

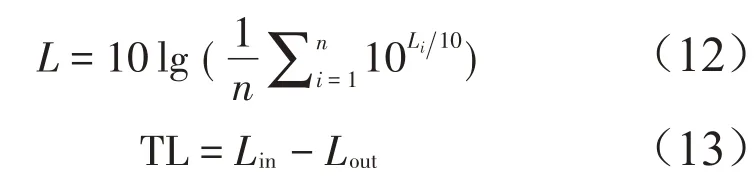
2 周期导管的带隙及振动特性

在周期结构的第一带隙中，由于长行波与振子的谐振特性相互作用时发生共振，产生带隙。在谐振频率下，起始频率一般由“振子等效质量-振子等效刚度-固定端”模型决定，而截止频率则由“振子等效质量-振子等效刚度-基体等效质量”模型决定，在刚度作用下，模型中的两质量会做出反向位相对运动[11-12]。

以某海洋平台为研究对象，如图1所示，其主要结构为导管及钢板，总高度为65 m，长和宽为36 m，一共三层，单层高20 m，底部支撑脚高5 m，顶部有一层2 mm厚的钢板，即工作区域。结构的其他参数如表1所示。

图1 海洋平台桁架结构示意图

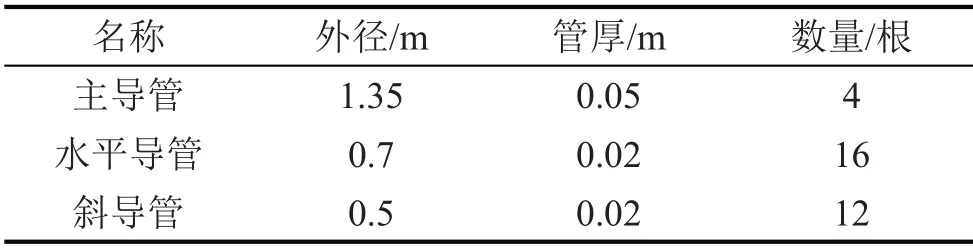
表1 海洋平台导管的主要参数

周期导管结构如图2（a）所示，由10 个单元组成，每个单元长3 m，相邻两个单元组成一个周期导管晶格，如图2（b）所示，A、B 厚度分别为3 mm 和8 mm。

图2 海洋平台桁架结构示意图

周期主导管的基本单元如图2（b）所示。海洋平台桁架结构由10个周期单元组成，每个周期导管晶格单元常数a为6 m。周期主导管的A、B 两段对应的厚度分别为3 mm 和8 mm，A、B 两段的长度a1、a2都为3 m。周期主导管结构的弯曲振动与纵向振动对应于海洋平台桁架结构在径向和轴向2个方向激励下的响应。

为了探究周期导管的壁厚对带隙的影响，通过平面波展开法，计算一维周期导管的带隙。设导管A、B的厚度为a（3 mm和5 mm）、b（3 mm和8 mm）、c（6 mm 和9 mm）、d（6 mm 和10 mm）四种组合，分别建立模型进行仿真分析，处理结果如下图3所示。

由图3 可知，不同壁厚组合的晶格对带隙宽带有着较大影响；由于共振频率决定带隙的起始频率，不同壁厚组合的晶格会改变单元质量，b 相较于a，单元质量增大，共振频率降低，起始频率会向低频偏移，提前56 Hz，同时截止频率延后75 Hz，引起带宽增大了131 Hz；b、c、和d 三种组合的起始频率都在300 Hz附近，由于b组合的截止频率相对较高，因此其带隙宽度也最大，为282 Hz。

选用b（3 mm 和5 mm）组合晶格排列成5 个周期导管，计算其轴向和径向激励时的传递特性。边界条件设两端自由，一端施加面激励，另一端提取面响应，分析频率为0～1 000 Hz，步长为2 Hz，结果如图4所示。

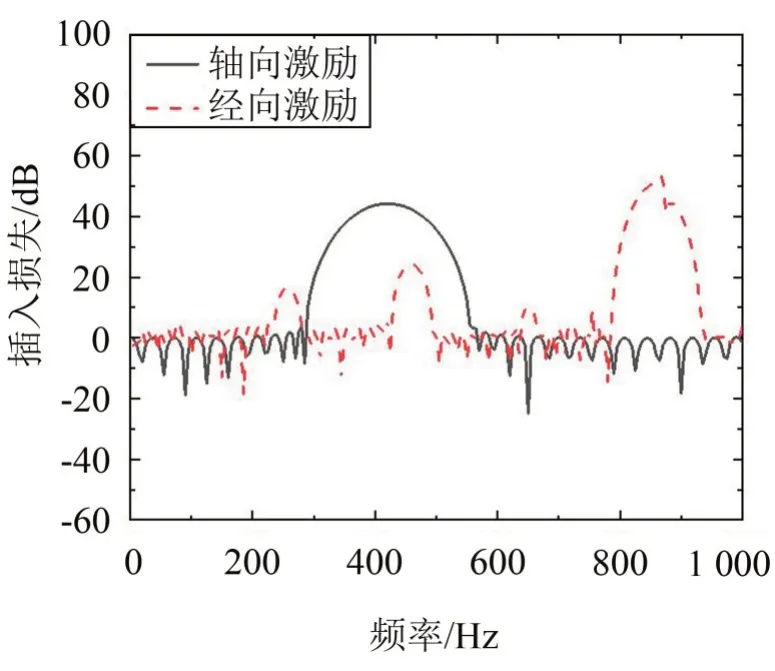
图4 不同激励下插入损失

由图4可知，两种激励方式都存在带隙，其中轴向激励时的第一带隙宽带最大，为282 Hz，其插入损失峰值达到45 dB；而径向激励时第一带隙起始频率比前者提前70 Hz，但带宽较小，其插入损失峰值发生在第三带隙上，为53 dB。

通过以上对导管晶格及周期导管的带隙分析可知，b（3 mm 和8 mm）组合壁厚的带宽最大，且起始频率相对较低，具有较好的减振性能，因此，用这个组合尺寸的周期导管代替传统导管将更好地提高海洋平台的减振性能。

3 海洋平台周期桁架结构振动特性

周期桁架结构主要由主导管、水平导管及斜导管组成，根据周期导管的带隙特点，将桁架的导管设计为全周期导管结构[13-14]，其有限元模型如图5所示。

图5 周期桁架结构激励和响应位置

海洋平台会受到地震载荷的作用[15]，本节分析海洋平台受地震波的影响，地震波选用EI-Centro波[16]。

比较传统桁架结构和周期桁架结构在地震载荷下的减振性能，在海洋平台的支撑脚处施加地震载荷激励，提取顶层钢板面加速度响应。由响应值处理得到顶层工作区域平均振级曲线（基准值为a0=10-6m/s2）如图6和图7所示。

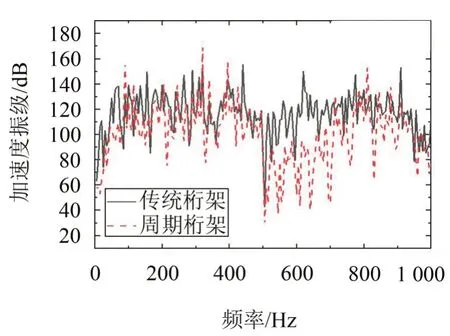
图6 海洋平台工作区域加速度振级曲线（轴向）

由图6和图7可知：在0～1 000 Hz频段中，周期桁架结构的加速度振级明显低于传统桁架；从轴向上看，在495 Hz～700 Hz频段上，加速度振级降低较明显，整个频段上，周期桁架的加速度平均振级比传统桁架降低约16.1 dB；从径向上看，整个频段上，周期桁架的加速度振级都有所降低，平均振级比传统桁架降低约14.6 dB；因此周期导管应用到海洋平台桁架结构中，减振效果提升明显。

图7 海洋平台工作区域加速度振级曲线（径向）

4 周期导管晶格常数对桁架减振性能的影响

导管晶格的尺寸将直接影响导管周期的个数，本节主要研究组成周期导管晶格的尺寸对海洋平台减振性能的影响[17]。

导管A和导管B的长度保持相同，壁厚为3 mm和8 mm，组成一个导管晶格，取导管晶格长度为6 m、8 m 和10 m 作为研究对象。由于桁架结构的尺寸不变，导管的总长度都不会变化，当晶格长度增加时，导管的周期个数将会减小。分别对周期桁架结构施加轴向和径向激励，分析导管晶格尺寸对减振性能的影响，曲线对比如图8和图9所示。

图8 导管晶格尺寸对桁架减振性能的影响（轴向）

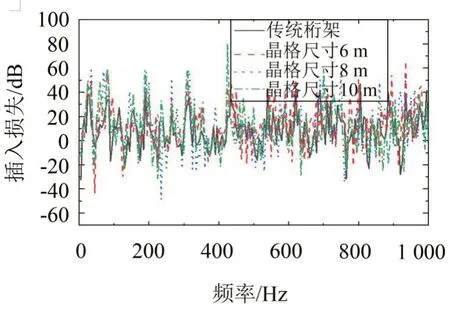
图9 导管晶格尺寸对桁架减振性能的影响（径向）

由图8 可知：晶格尺寸为6 m 时，在498 Hz～770 Hz有明显带隙产生，其宽度为272 Hz；晶格尺寸为8 m 和10 m 时未出现明显带隙情况，这是由于晶格尺寸较大，导管的周期数量太少而无法形成带隙；晶格尺寸为6 m 时的周期桁架结构在0～1 000 Hz频段内的减振效果最好，比传统导管桁架结构提高了4.5 dB。

由图9 可知：在0～1 000 Hz 频段内，周期桁架的振级落差曲线图上没有发现明显的带隙存在；随着晶格尺寸的增大，周期数量减少，海洋平台周期桁架结构的减振效果也逐渐降低，从12.9 dB 衰减到10.2 dB，但相较于传统桁架结构的8.3 dB，周期桁架的减振效果都有所提高。

A 导管和B 导管壁厚为3 mm 和8 mm，晶格尺寸为6 m，不同方向激励时。桁架结构的强度最佳且减振效果最好。