倾斜角影响下磁悬浮双转子系统的振动分析

万雨初，朱由锋，韩 隆，靳赞成

（1.山东科技大学 交通学院，山东 青岛 266590；2.山东科技大学 机械电子工程学院，山东 青岛 266590）

双转子系统被广泛应用于燃气轮机和航空发动机等动力设备[1-2]，而使用磁悬浮轴承[3]取代传统的滚动轴承作为系统的支撑，可以进一步提高其性能，这也成为近年来该领域一个重要的发展方向。

对双转子系统的振动行为进行分析是当下的研究热点。Ebrahimi 等[4]根据拉格朗日方程推导出磁悬浮双转子系统动力学模型，研究了转速、轴速比和重力参数对其动力学行为的影响。Chen等[5]分析了不同基座运动参数对双转子系统瞬态不平衡响应的影响。陈毅等[6]建立了双转子系统在复杂机动飞行环境下的动力学模型，并对该模型的正确性和适应性进行了验证。此外，部分学者围绕特殊工况下转子-轴承系统的行为展开了研究。刘占生等[7]对卧式布置的转子进行有限元建模，对不同倾斜状态下滑动轴承径向载荷引起的动力学行为变化进行了仿真分析和实验验证。李默等[8]研究了横倾角对非对称支撑的转子-轴承系统的影响，发现径向力因重力的重新分配而变化，继而对系统稳定性产生了影响。

上述研究并未对立式布置的转子-轴承系统的倾斜工况展开研究，而当磁悬浮双转子系统受到外部激励时，倾斜角的存在使得转子的运动变得更为复杂。为表征在以上特殊情况下转子的动力学特性，本文建立倾斜角影响下的磁悬浮双转子系统的动力学模型，通过仿真分析转速比和倾斜角等因素对系统振动特性的影响。

1 系统模型的搭建

1.1 磁悬浮双转子系统结构

航天器和车辆等安装平台在运行过程中因受到随机激励都会做出一定的响应，其响应会影响定子的运动。磁悬浮轴承固定连接在定子上，与转子之间会产生相对位移。而转子在旋转过程中由于受到不平衡力[9]等各种因素影响，其自身的运动也会导致与磁轴承之间的相对位移。根据电磁力公式，电磁力作用到转子上，重新调节转子的位置，直至转子达到稳定悬浮状态。

本文建立存在外部激励的系统10 自由度力学模型，即定子的1个垂直自由度，低压和高压转子质心分别沿X、Y方向的运动以及俯仰、侧倾运动共8个自由度，以及将双转子视为一个整体的沿轴向运动的1个自由度。

磁悬浮双转子系统结构如图1所示。

图1 磁悬浮双转子系统模型

图1 中ms为定子质量，ks、cs分别为悬置定子的弹簧刚度系数和阻尼系数，q为定子所受到的激励，θ为转子Z轴与铅垂线的夹角，β为铅垂线在XY平面的分量与X轴的夹角，ω1和ω2为低压和高压转子的转速，kt、ct分别为中介轴承的刚度和阻尼系数。低压转子质心的五个自由度分别为沿X轴的位移x1，沿Y轴的位移y1，绕X轴转动角度θ x，绕Y轴转动角度θy，沿Z轴的位移z。高压转子质心的五个自由度分别为沿X轴的位移x2，沿Y轴的位移y2，绕X轴转动角度φx，绕Y轴转动角度φy，沿Z轴的位移z。A、B、C、D 分别代表四个磁轴承，磁轴承A、B 到低压转子质心的距离分别为l1、l2，磁轴承C到高压转子质心的距离为l3，中介轴承到高压转子质心的距离为l4，磁轴承B到中介轴承的距离为l5。

则低压转子在磁轴承A、B 上沿X、Y方向的位移，高压转子在磁轴承C 上沿X、Y方向的位移以及两个转子在磁轴承D 上沿Z轴的共同位移可表示为：

1.2 电磁支承力

一般采用对称布置磁轴承的形式使得磁悬浮转子实现稳定运动，这就形成一种差动的形式。磁轴承的差动电磁力公式[10]如下：

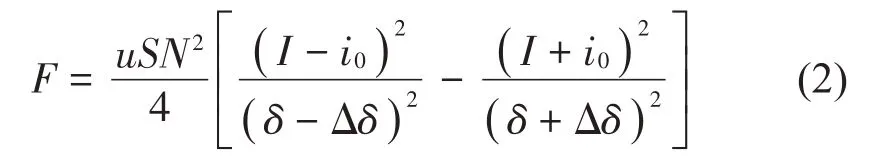
其中：u为空气导磁率，S为有效磁面积，N为线圈匝数，I为偏置电流，δ为空气间隙，i0为转子处于非平衡位置时恢复到稳定位置时的控制电流，Δδ为定子相对于磁悬浮转子位移改变值。

对差动电磁力公式进行泰勒展开即可得电磁力与励磁电流及磁悬浮转子位移的关系：

位移刚度和电流刚度分别为：

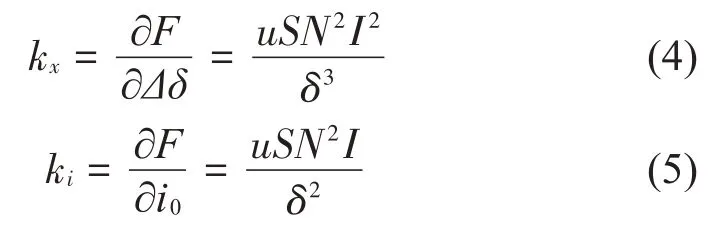
i0是关于Δδ的函数，采用的控制方式不同则函数的形式不同，在这里采用的是工业上较为成熟的PD 控制策略，kp和kd分别为比例和微分增益。其函数形式为：

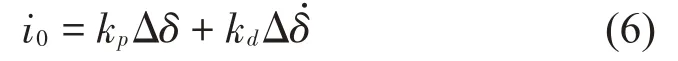
综上可得磁轴承在PD 控制策略下所提供的电磁力如下：

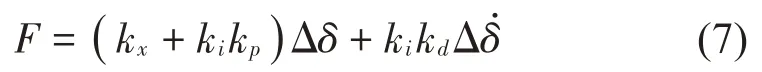
即：

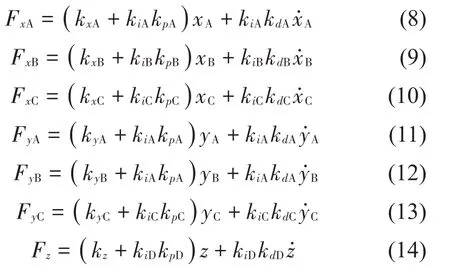
1.3 激扰力

将安装平台和定子简化为一个直接受到外部激励的定子，该定子受到激励q后会产生振动位移zs，其受到的外部激励q为：

定子受到外部激励后会产生微小运动，继而改变与磁悬浮转子之间的间隙，此过程可看作是激扰力f的作用，因定子和转子的相对位移以定子位移改变为主，故可认为激扰力是由定子位移的改变而引起的，定子在各方向的位移改变值是根据定子的铅垂线方向位移zs沿各个方向分解而来：

激扰力可被视为外部激励，且为本文重点研究对象，故不作线性化处理，激扰力如下：

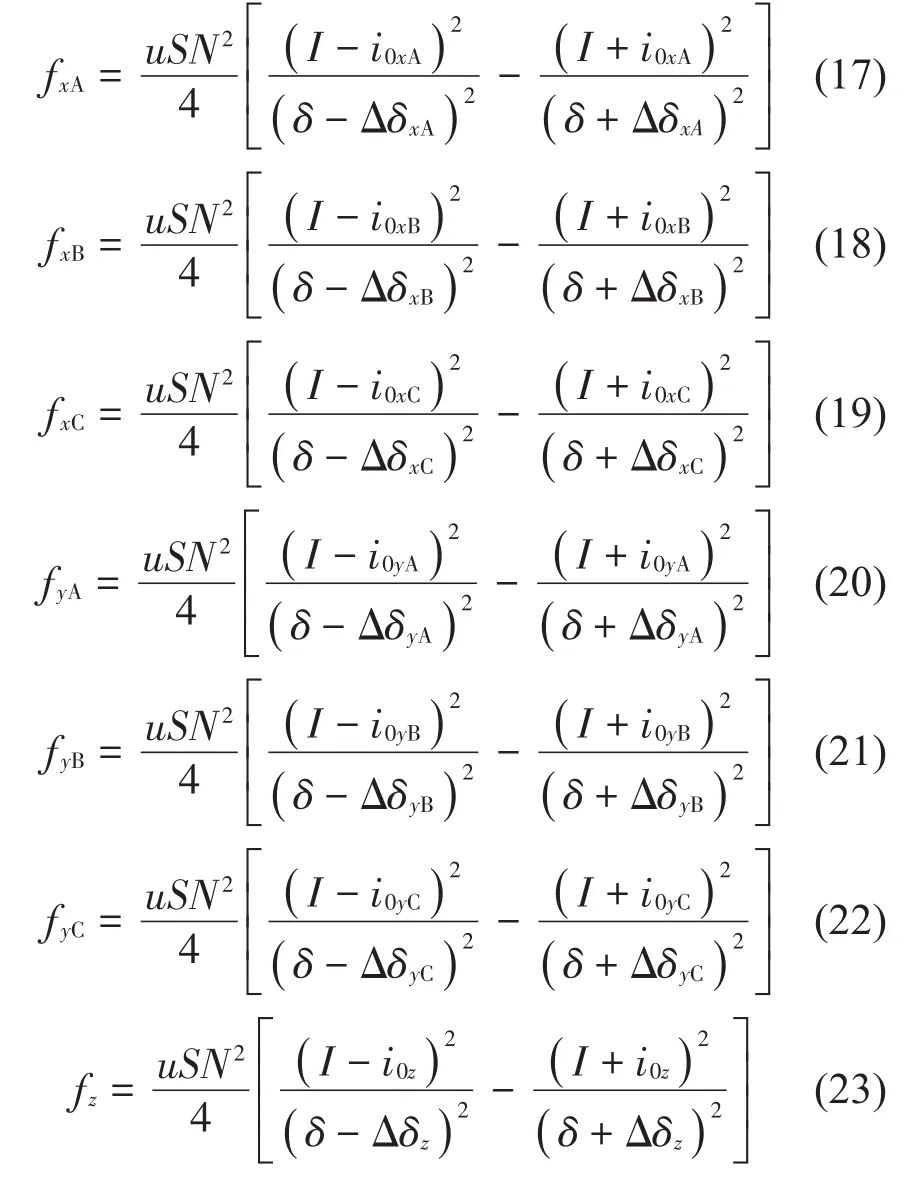
1.4 中介轴承力

本文以线性弹簧和阻尼器的并联为连接低压和高压转子的中介轴承[11]，其内外转子间在X轴和Y轴的作用力分别为Fx和Fy。

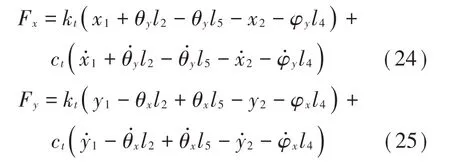
1.5 磁悬浮双转子系统动力学方程

根据以上力学模型，得系统微分方程：

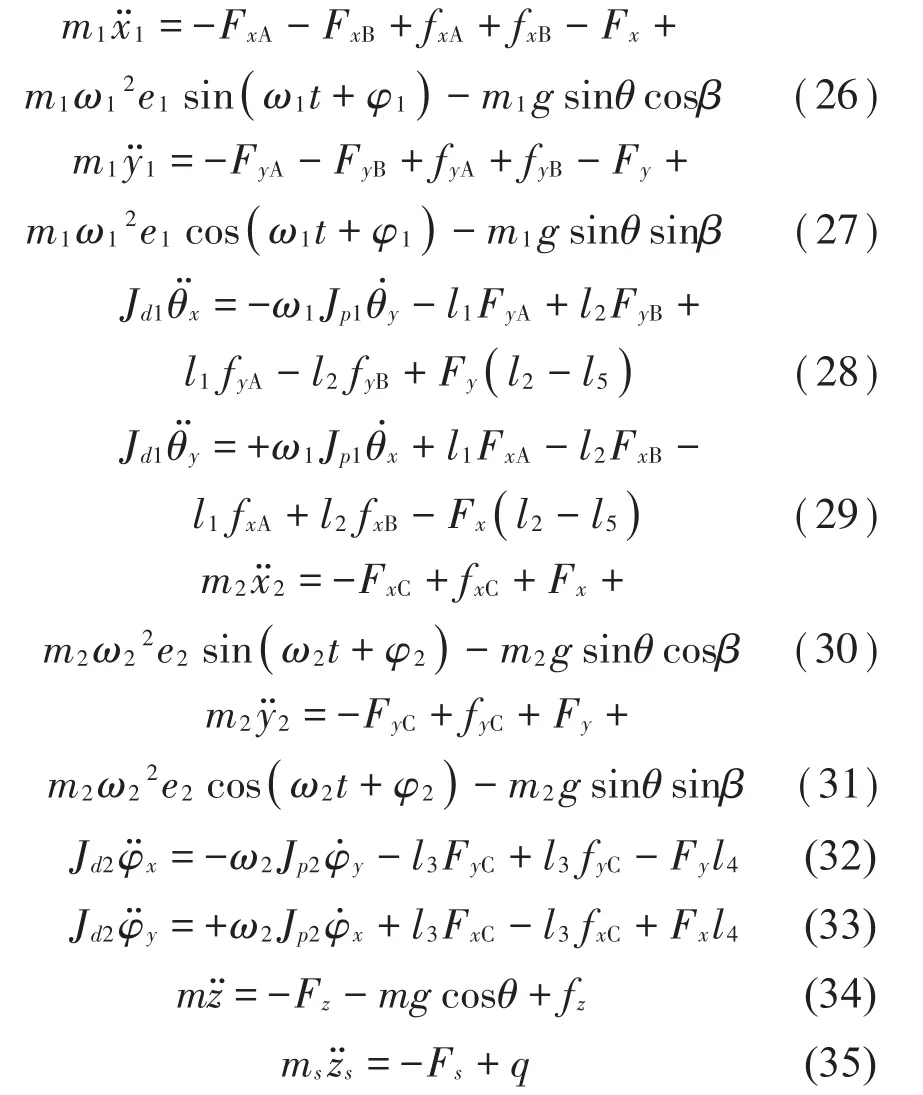
式中：下标1 和下标2 分别表示低压转子和高压转子，m1和m2为其质量，e1和2为其偏心距，φ1和φ2分别为其偏心距与自转坐标系的夹角，Jd1和Jd2为其直径转动惯量，Jp1和Jp2为其极转动惯量，m为低压和高压转子的质量之和：m=m1+m2。

2 振动响应分析

磁悬浮双转子系统中的各参数取值如表1 所示。综合考虑刚性转子平衡精度标准IS0 1940划分的不平衡精度等级和本文的研究情况，设定e1=4 μm，e2=3 μm，φ1=φ2=π/2。

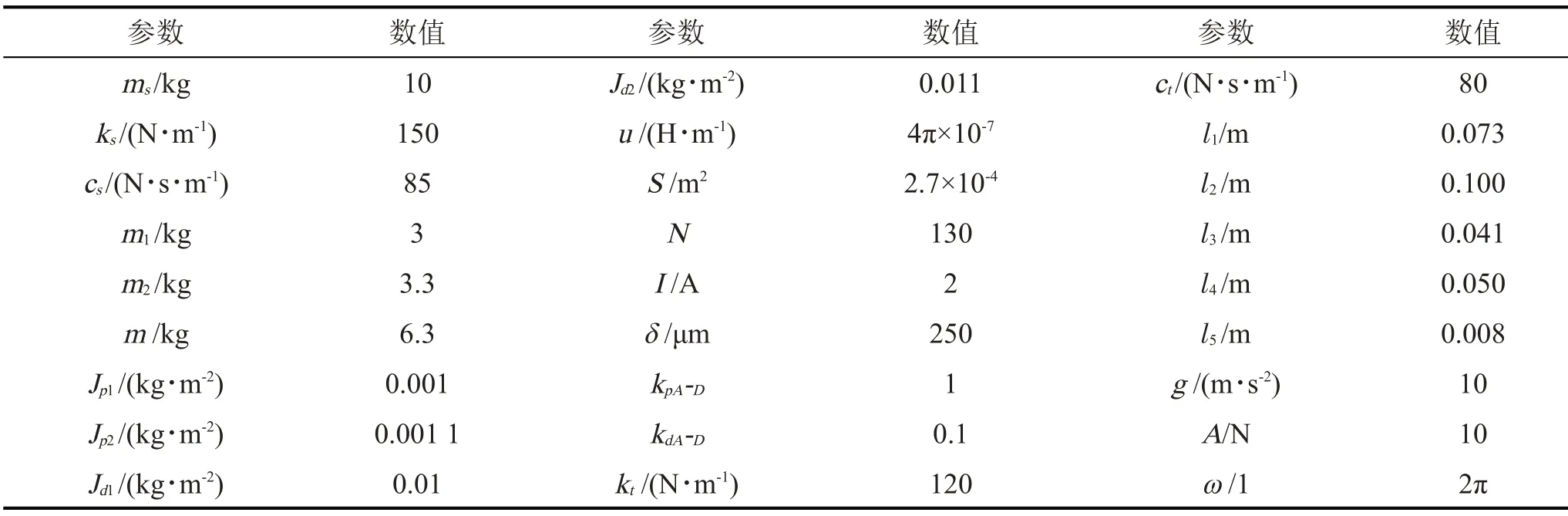
表1 系统相关参数

通过MATLAB仿真软件中4阶龙格库塔法对建立的系统10自由度微分方程进行数值分析，设定低压和高压转子转速ω1=ω2=20 rad/s，倾斜角θ=0°，得到低压转子的质心运动轨迹，如图2所示。

根据图2可以看出，转子质心沿Z轴呈现螺旋下降的趋势，并最终在-6×105μm位置处保持稳定运动，转子之所以做圆周运动是因为在X-Y平面始终存在由于不平衡力激励而产生的振动；而转子在Z方向受重力和激扰力二者共同作用，在磁轴承的电磁力的不断调整下，最终处于平衡状态。

图2 低压转子质心运动轨迹图

由于转子在Z方向主要受重力和激扰力影响，而决定其大小的倾斜角在改变不大的情况下，Z轴的振动响应基本不变，故接下来将分析低压转子在X-Y平面的动力学行为。

根据图3（a）可以看出，转子在X方向的最大振动幅值约为1.5 μm，呈现出周期运动的趋势。从图3（b）可以看出，转子的运动轨迹呈现为一偏移的椭圆形，且最终实现较为稳定的运动状态。

图3 低压转子质心的时间历程图和X-Y平面运动轨迹图

基于系统的特点，接下来将分析转速比与倾斜角对系统振动响应的影响。

2.1 转速比变化对双转子系统的影响

低压与高压转子的转速比不同会引起低压转子动力学行为的变化。选取θ=0°，取低压转子的转速为20 rad/s，改变高压转子的转速并观察转速比变化所产生的影响。

通过图4可以看出，随着转速比的增大，转子在X-Y平面的运动轨迹形状从椭圆形趋向复杂化，逐渐呈现“花瓣状”。

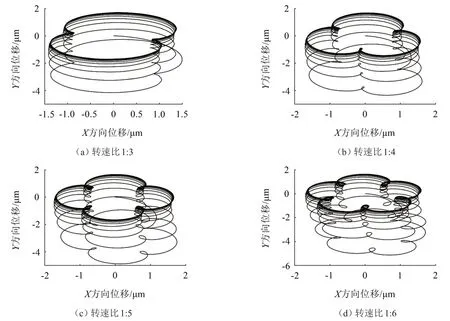
图4 不同转速比下低压转子质心在X-Y平面运动轨迹图

2.2 倾斜角变化对双转子系统的影响

当转子轴线与铅垂线存在一定的夹角，即θ≠0°时，由定子位移所产生的激扰力和重力都会对转子在X、Y方向的位移产生影响，从而导致转子的动力学行为发生变化。取低压转子转速ω1=20 rad/s，转速比为1:1，取β=45°，即把激扰力和重力的影响在X轴和Y轴进行平分。研究θ的变化对转子动力学行为的影响。

通过图5 可以看出，随着θ的不断增大，转子在X-Y平面的圆周运动的半径逐渐增大，沿轴线的偏移距离也增大，并最终在平衡位置处做圆周运动，且轴线不断向45°靠近。

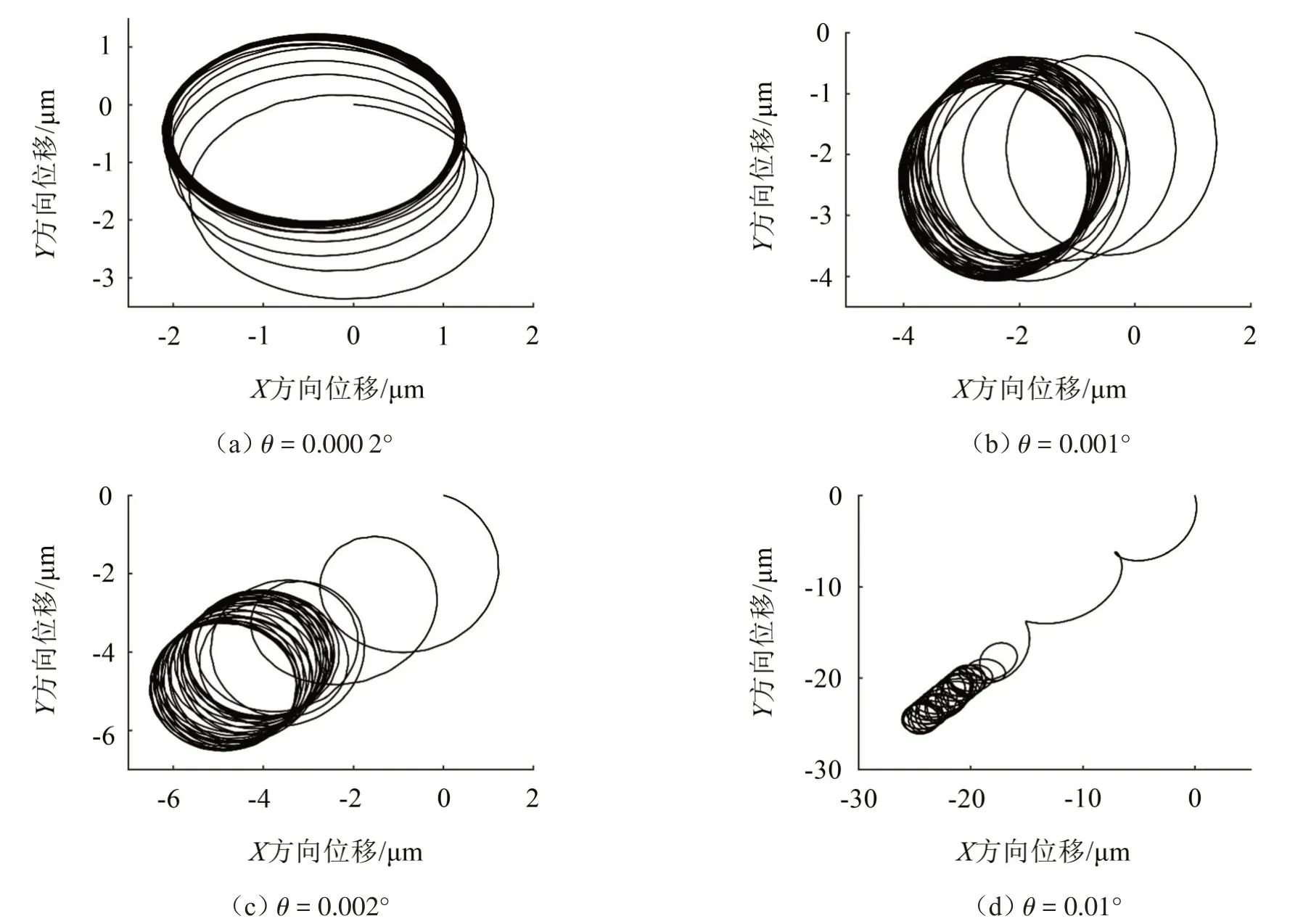
图5 不同倾斜角下低压转子质心X-Y平面运动轨迹图

这是因为随着倾斜角的不断增大，重力和激扰力对X-Y平面的影响越来越大，越发起到主导作用。重力导致沿轴线的偏移距离增大，随着磁轴承的不断调整，最终使得转子在重力于X-Y平面的分配值处做稳定的圆周运动。而来自激扰力的激励增大了转子的最大振动幅值，即增大了圆周运动的半径。且由于设定β=45°，轴线不断向45°靠近。

3 非线性分析

磁悬浮双转子系统中存在的不平衡力和激扰力等非线性因素可能会导致转子产生一定的非线性振动，非线性振动会对系统的稳定性和安全性产生较大的威胁，所以在研究转子响应时是不可忽略的方面。

3.1 转速比对双转子系统稳定性的影响

转速会导致不平衡力增大，为研究转速与系统稳定性的具体关系，现以低压转子的转速ω1作为分岔参数研究转子振动响应的分岔过程。

由图6（a）可以看出，随着转速的增加，系统依次经历了不同的运动状态。在转速区间（0～400）rad/s 内系统为概周期运动，在转速达到500 rad/s 时系统演变为混沌运动，随后振动位移逐渐收敛，进入拟周期状态。

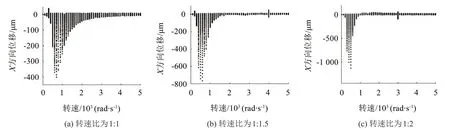
图6 不同转速比下的转速分岔图

由图7 可以看出，低压转子的庞加莱截面图呈现发散的趋势，故可判断该转速下，低压转子处于不稳定运动状态。

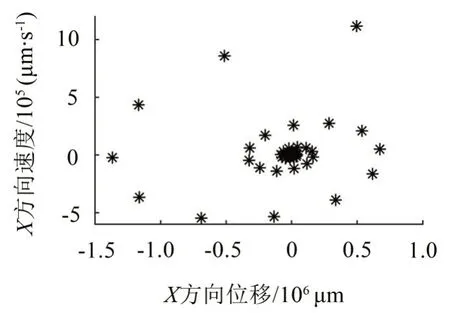
图7 低压转子庞加莱截面图（转速600 rad/s）

通过图6（b）和图6（c）可以看出，转速比的增大降低了转子进入混沌运动的转速，当转速比由1:1增大到1:1.5 和1:2 时，转子进入混沌运动状态的转速从500 rad/s分别降低到400 rad/s和300 rad/s，即转速比的增大会使得转子的不稳定性增大。

3.2 倾斜角变化对双转子系统稳定性的影响

激励q的频率ω会使得非线性激扰力发生变化，故以激励频率ω作为分岔参数研究转子振动响应的分岔过程。

当θ=0°时，非线性激扰力不对X-Y平面产生作用，故不受激励频率变化影响的低压转子将一直处于稳定的周期运动状态。通过图8（a）可以看出，倾斜角的存在使得转子的运动状态发生改变。系统在激励频率区间（34～45 和50～84）rad/s 内两次进入失稳的混沌状态，在其他区间则处于周期运动、概周期运动、倍周期运动交替进行的状态中，系统较为稳定。

由图9 可以看出，低压转子的庞加莱截面图为散乱的点集，故可判断该激励频率下，低压转子处于不稳定运动状态。

图9 低压转子庞加莱截面图（激励频率70 rad/s）

通过图8（b）和图8（c）可以看出，转子的径向振动位移随θ的增大而持续增大，但系统经历了不同运动状态的激励频率区间未发生变化，即倾斜角的变化对转子稳定性基本无影响。

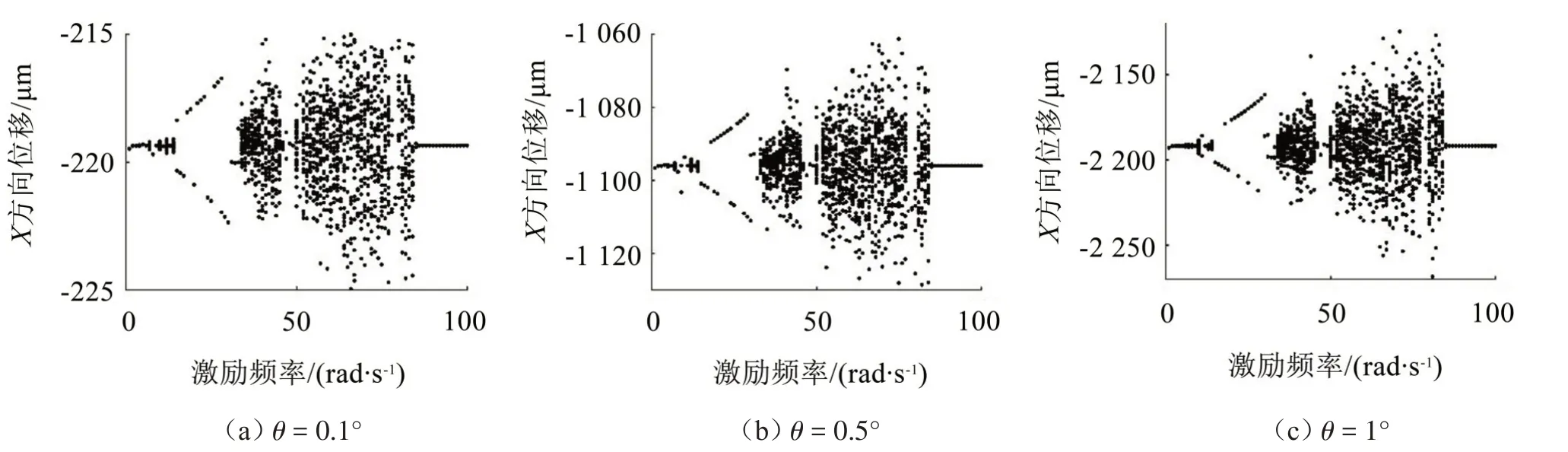
图8 不同倾斜角下的激励频率分岔图

4 结语

本文建立了倾斜角影响下的磁悬浮双转子系统10自由度动力学模型，通过为系统添加外部激励进行仿真分析，得到以下结论：

（1）转子质心沿Z轴呈现螺旋下降的趋势，并最终围绕重力的平衡位置进行稳定的上下振动。

（2）转速比和倾斜角的增大均会增大转子到达平衡位置前沿轴线的偏移距离。不同的是，转速比的增大会使轴心运动轨迹形状变得更为复杂；而倾斜角的增大会增大圆周运动的半径，即最大振动幅值，同时倾斜角还会改变轴线的角度。

（3）转速比的增大降低了系统进入混沌运动状态的转速范围，即降低了系统稳定性；倾斜角的存在使得系统随着激励频率的增加而产生不同的运动状态，但倾斜角的增大仅增大其振动幅值，对稳定性无影响。