基于PID型迭代学习控制算法的皮层网络节律调制

王佶宣，邓 斌，王 江，伊国胜

基于PID型迭代学习控制算法的皮层网络节律调制

王佶宣，邓 斌，王 江，伊国胜

(天津大学电气自动化与信息工程学院，天津 300072)

皮层网络节律是大脑动力学的普遍特征，它与认知和记忆功能密切相关．异常大脑节律通常伴随着癫痫、帕金森等疾病的产生．通过电刺激能有效调制异常脑节律，进而减轻疾病症状．目前常用的是开环电刺激调制方法，刺激能耗高且无反馈信息，难以实现个性化有效调制节律．为了实现自适应调制皮层节律，构建皮层网络的平均场模型，产生不同节律的自发振荡活动．首先，以通过PID型学习律处理的实际和期望主频的差值作为反馈变量，采用PID型迭代学习控制算法实时自适应调制40Hz电刺激的幅值，实现了将主频从theta节律调制到alpha节律．其次，利用开环控制、PID控制与PID型迭代学习控制方法，对不同个体和相同个体的节律分别进行调制，证明PID型迭代学习控制具有最优的个性化调制结果．然后，利用数值仿真实验验证了PID型迭代学习控制能将delta、theta和gamma节律的任意主频调制到alpha节律．最后，从理论推导方面对PID型迭代学习控制算法进行了收敛性分析，证明该方法在理论上的有效性．本文研究从数值仿真和理论推导两方面，证明了PID型迭代学习控制算法能通过控制电刺激振幅，进而有效调制大脑皮层节律至alpha节律，具有较好的个性化调制结果，进一步为临床通过闭环控制治疗节律异常疾病提供了方法指导.

节律调制；皮层网络；迭代控制；闭环控制

大脑节律是指神经元活动的不同模式，它与特定行为、睡眠状态相关，通常通过测量神经元集群的场活动来得到节律[1]．局部场电位(local field potential，LFP)是测量大脑节律的一种有效方法，LFP反映了大脑内局部兴奋性和抑制性神经元突触后电位的和，代表神经集群局部的协同作用．通过傅里叶分析等方法能将LFP记录的局部神经集群振荡电活动转化为大脑节律信号．通过LFP测量所得的大脑节律主要分为delta节律(1～3Hz)、theta节律(4～7Hz)、alpha节律(8～12Hz)、beta节律(13～30Hz)和gamma节律(30～100Hz)[2]．不同的大脑节律与生理状态、认知功能以及病理状况密切相关．例如，theta节律与记忆相关，alpha节律与认知相关．alpha节律在认知过程中具有重要意义，该节律的削弱甚至消失是多种脑疾病的生理表现，通过调制主频至alpha节律能有效增强认知功能[3]．目前通常利用深部脑电刺激(deep brain stimulation，DBS)调制大脑节律．通过DBS调制神经元集群活动，能有效增强alpha节律振荡并改善大脑的认知功能[4]．因此研究如何利用电刺激调制alpha节律对治疗脑节律异常疾病具有重要意义.

电刺激调制节律分为开环和闭环控制，临床中最常用的是开环电刺激．开环控制的刺激参数调制困难，通常刺激装置的参数在植入大脑后由经验丰富的医生设置，整体调制时长，至少需要长达6个月才能达到较为理想的结果[5]．且由于手术困难、易感染和调制参数不便等不利因素，导致在开环控制方法下节律的调制实时性较差、调制耗时长、调制结果难以预测并且调制过程严重依赖医生经验．这些不利因素可能对大脑的节律活动，甚至是患者身体健康造成有害影响．开环电刺激调制过程简单，虽然最终能通过改变刺激频率和幅值使网络主频被调制到目标主频[6]，但是开环控制对调制结果的可控性较弱，调制结果高度依赖刺激参数．由于开环控制自适应调控刺激参数的能力较弱，通常是通过试错来确定最终参数设置[7].因此需要设计一种控制方法，既能实时调制大脑节律到期望节律，又能快速自适应调节刺激参数，减小不利刺激对大脑的影响．

闭环电刺激调制方式在调制大脑节律方面具有优势．不但能实现实时检测大脑系统的动态变化，自动调制大脑节律并优化刺激参数，而且能有效缩短无效电刺激的作用时长，降低刺激能耗．目前，通过闭环控制大脑信号的难点是如何选取控制信号和反馈信号[8]．电刺激振幅参数通常被选取作为控制信号，通过调节该参数能有效控制异常神经元集群活动．利用含外部输入自回归模型构建自适应最小方差控制器，能通过闭环控制有效调控DBS幅值，使异常神经元放电活动正常化[9]．此外，在动物实验中，通过DBS控制刺激幅值也能实现自动检测大鼠海马区癫痫电信号，有效调制异常癫痫信号[10]，改善大鼠大脑异常节律振荡．因此，基于上述研究基础，本文选取电刺激幅值作为控制信号，通过闭环控制实时调控大脑节律．此外，反馈信号的选取对调控效果也至关重要．研究表明皮层网络平均场电位变化与节律变化高度相关[11]，通过计算平均场电位的频率分布范围，能直观表示皮层网络所处的节律区间，利用平均场电位计算出的网络主频直接决定网络所处的节律范围，因此本文采用平均场电位的主频信号作为反馈信号．

迭代学习控制(iterative learning control，ILC)非线性强，鲁棒性好，适用于建模困难和具有重复性变化的对象[12]．在ILC系统中只需给出输入和输出信号，简化了被控对象动态变化的复杂性．由于平均场电位呈现重复性变化，而且对皮层网络施加的电刺激也表现为周期性变化，因此传统PID控制难以满足对皮层网络这些重复性活动的非线性控制需求．ILC方法在控制重复性运动中表现出显著的优势，而且它不依赖被控对象的具体模型，能实现有限时间上的完全跟踪．ILC方法已被证明能抑制和修正异常放电活动，使丘脑神经元的放电活动从异常恢复到正常状态．此外，通过添加遗忘因子进而改进ILC方法，对小世界网络的场电位进行控制，实现了场电位信号跟踪期望波形信号[13]．将PID控制理念运用于ILC方法中是目前常用的控制方法之一，利用PI型迭代学习控制方法能使HH神经元和ML神经元的实际输出跟踪期望轨迹放电[14]．而且利用PI型迭代学习控制方法也能消除PR模型中异常的放电活动[15]．进一步改进PI型迭代学习控制方法，将其与无迹卡尔曼滤波器结合，能调节单神经元的癫痫样放电，使异常的病态放电波形正常化[16]．综上所述，ILC方法控制效果好，能平稳控制真实信号跟踪期望信号，具有更高更平稳的响应速度．虽然ILC已被广泛应用于控制神经元网络中的对象，但目前利用ILC实时调控皮层网络节律变化的理论方法仍不完善．

为了实现实时自适应调制皮层网络异常节律，本文采用PID型迭代学习控制方法调控网络节律．文中主要分为3个部分：首先介绍皮层网络模型的构建方法；然后选择闭环控制的刺激频率，验证相应电刺激频率能否有效调制异常theta节律至期望alpha节律；接着分析对比不同控制方法的调制效果，证明PID型迭代学习控制方法在调制皮层节律方面的优越性；最后对实验结果进行收敛验证，并进行讨论和总结.

1 模型和方法

1.1 皮层网络模型

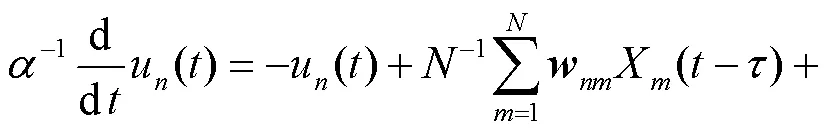
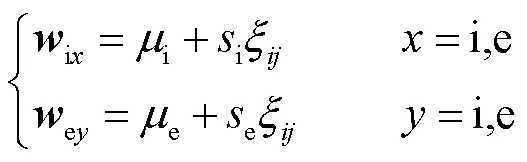
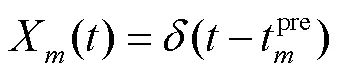
皮层网络中具有许多噪声，利用高斯白噪声能模拟该噪声，表达式为

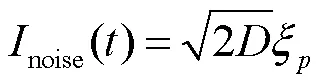
对大脑注入额外单阳极或单阴极刺激，会引起外部电荷注入会导致电荷失衡，造成不可挽回的损伤，因此采用电荷平衡的双向脉冲刺激能减弱该损伤．双向脉冲刺激的优势在于阴极脉冲和阳极脉冲的电荷输入量相等，使刺激对大脑注入的净电荷量等于零．双向脉冲刺激是较为可靠的刺激方式，能最大程度降低电荷注入对大脑损伤，本文采用的不对称双向电刺激表达式为

式中：和分别为阳、阴极刺激的强度，mA；和分别为阴、阳极脉冲间隔宽度，ms；为阴、阳极间时间间隔，ms．为了实现电荷平衡，实验选取的不对称双向脉冲的阴阳极具有不同的脉冲宽度，选取为的10倍，避免网络的振荡抑制现象产生[18]．不对称双向脉冲波形和相关参数设置如图1所示.

图1 刺激波形

1.2 平均场分析与计算

平均场电位是表示皮层网络活动变化的参数，它是模型中描述局部场电位的参数，平均场电位的计算公式为

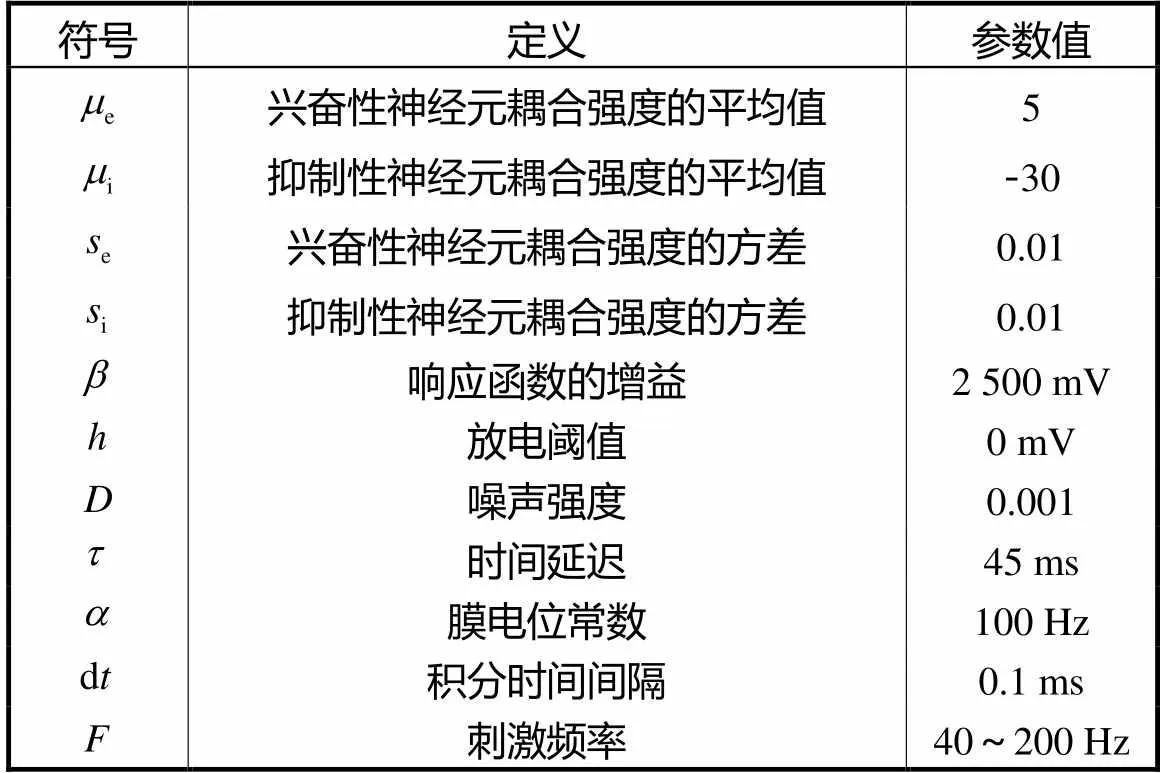
表1 模型参数设置

为了测试PID型迭代学习控制算法能否有效控制皮层网络节律，主要从以下3个步骤进行测试，相应的迭代学习控制流程如图2所示.

图2 迭代学习控制流程

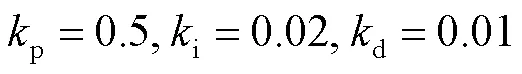
步骤2 进行PID型迭代学习控制，计算网络的平均场电位和迭代误差.

步骤3 计算相关频带总能量，通过功率谱密度分析计算节律主频大小．若迭代次数低于10次，储存误差并进行下一次迭代并返回步骤2；若迭代次数高于10次，跳出迭代循环．

1.3 PID型迭代控制算法

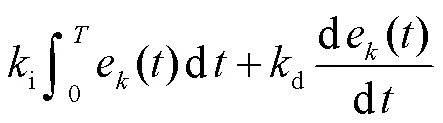
图3 PID型迭代学习算法结构

Fig.3 Structure of the proportional-integral-derivative-type iterative learning algorithm

2 结 果

2.1 闭环刺激频率选择

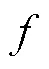
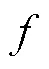
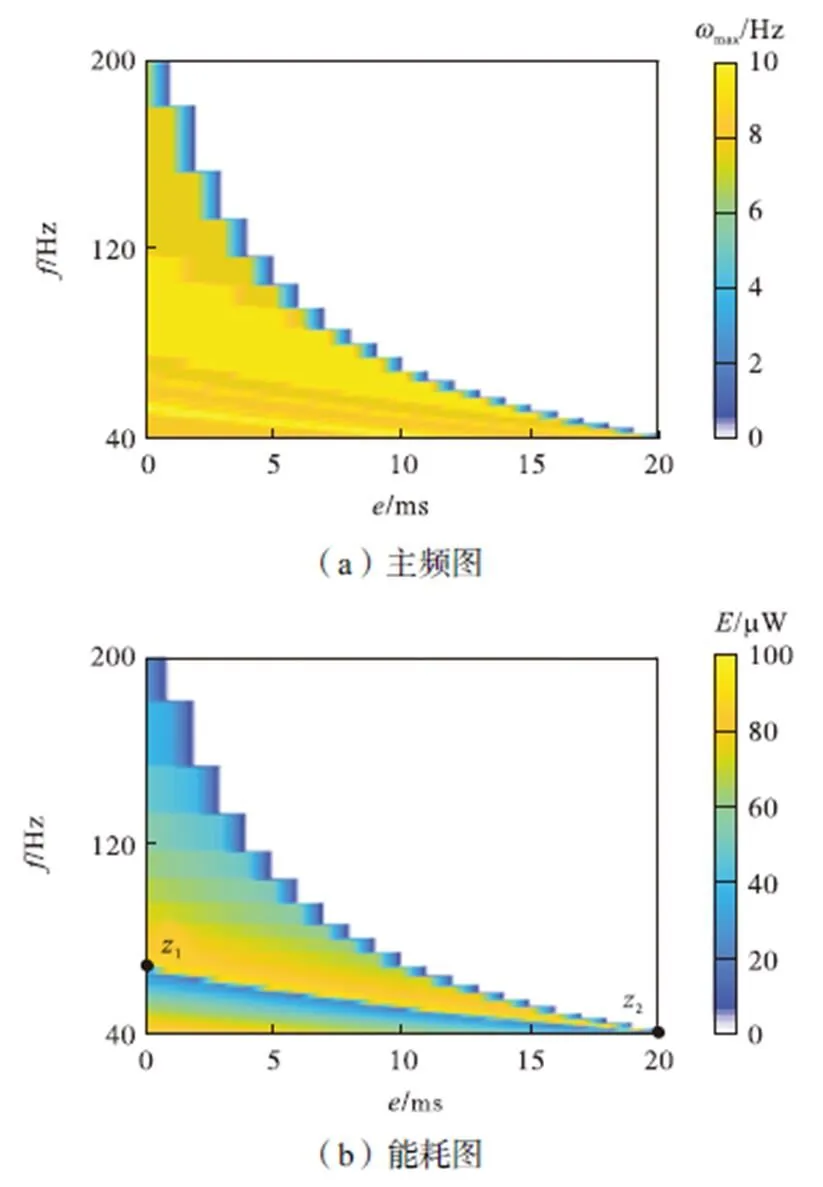
图4 刺激频率选择图

2.2 PID型迭代控制调制theta节律

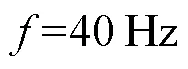
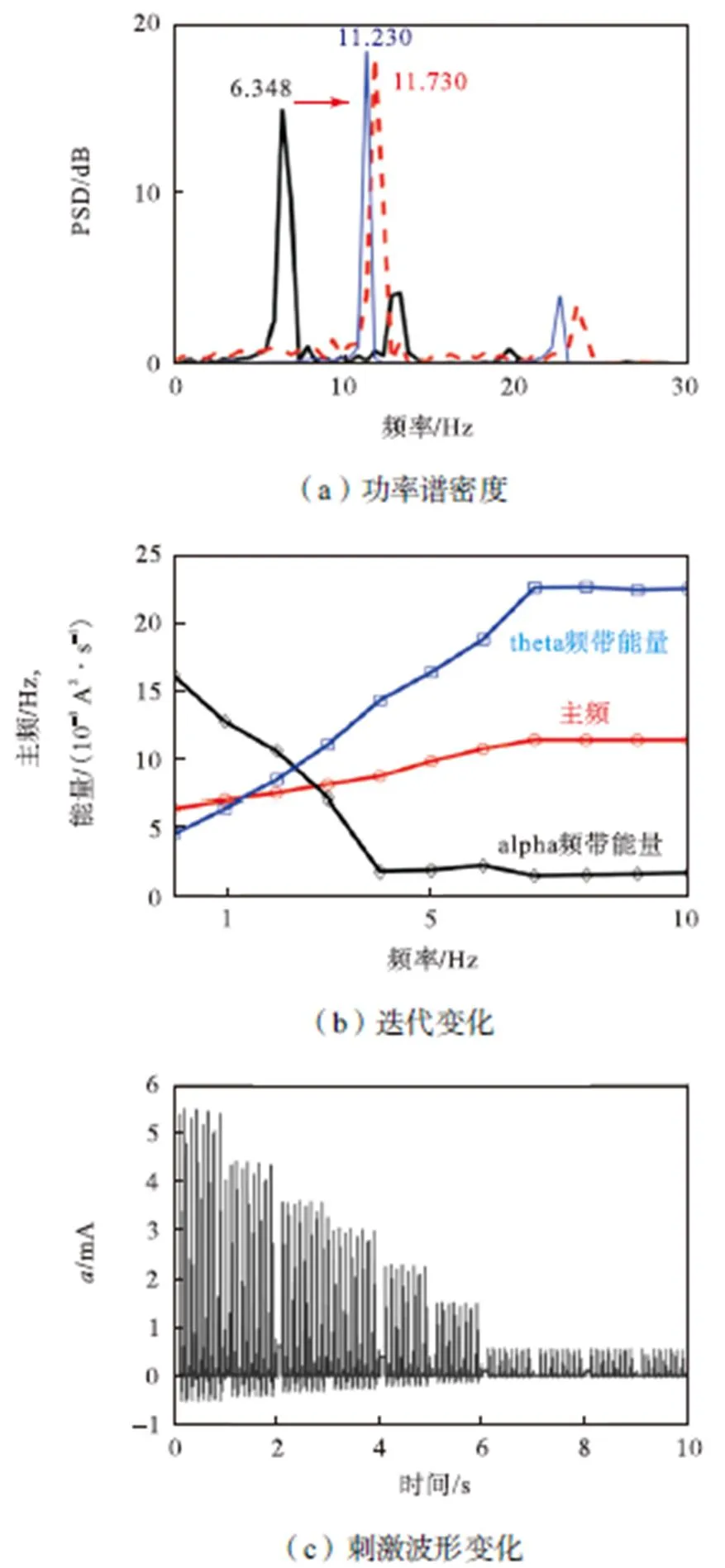
图5 刺激调制

在闭环控制起始位置处，皮层网络初始状态表现为theta频带能量最高和alpha频带能量最低，如图5(b)所示．随着迭代控制开始，期望主频和实际主频产生误差，将此误差信号反馈给皮层网络并不断进行反馈调制．在调制过程中，theta频带能量逐渐降低，而alpha频带能量逐渐上升，网络实际主频逐渐增大并靠近期望主频．调制结果表明，PID型迭代控制学习方法能有效调制网络节律．随着迭代次数的增大，刺激幅值不断降低，当迭代次数到达第7次时，网络状态趋于稳定，实际主频几乎等于期望主频．在随后的迭代过程中，实际节律实现对期望节律的跟踪，刺激幅值保持在较小的稳定值，稳定状态下刺激幅值几乎等于零，网络主频值最终保持在11.23Hz．仿真结果表明，PID型迭代学习控制能自适应调制刺激幅值，不但能有效减小异常刺激作用时长，降低刺激能耗，而且能有效调制皮层网络的节律．

2.3 不同控制方法调制相同节律

在相同的刺激条件下，能否灵活调制节律是衡量控制方法的关键因素．首先利用皮层网络模型产生相同的放电波形和网络主频用于模拟相同个体；然后利用不同的放电波形和网络主频表示不同个体；最后施加不同的电刺激，测试不同控制方法的调制效果．如图6～图8所示，黑色曲线表示初始状态，蓝色曲线表示调制结果，每幅图中的图(a)和(b)描述相同个体的不同状态，图(c)和(d)描述了不同个体的不同状态．对每个状态施加不同的电刺激，测试网络主频能否被调制到alpha节律．如图6所示，开环控制在任意刺激参数设置条件下，对节律的调制效果较差，无论是对于相同个体还是不同个体，都难以通过随机设置的初始刺激参数将theta节律调制到alpha节律．调制结果证明，虽然开环控制调制方法简单，但有效的刺激参数依赖经验设置，只有针对性的刺激参数才能将节律调制到alpha节律．相比于开环控制，PID控制表现较好．如图7所示，PID控制在随机的刺激参数设置条件下，能将大部分异常节律调制到期望节律，但仍有部分theta节律无法被调制至alpha节律．实验结果表明，相比于开环控制，闭环控制适应个体差异性的能力更强．如图8所示，相比于前两种控制方法，PID型迭代学习控制方法不但能实时调制网络节律，且调制准确率比PID控制更高，个体差异性的适应能力更强．结果表明，PID型学习律的迭代学习控制在实现自适应调制的基础上，进一步提高了对个体差异性的适应能力，具有更好的跟踪性能和更快收敛速度．

图6 开环控制调制

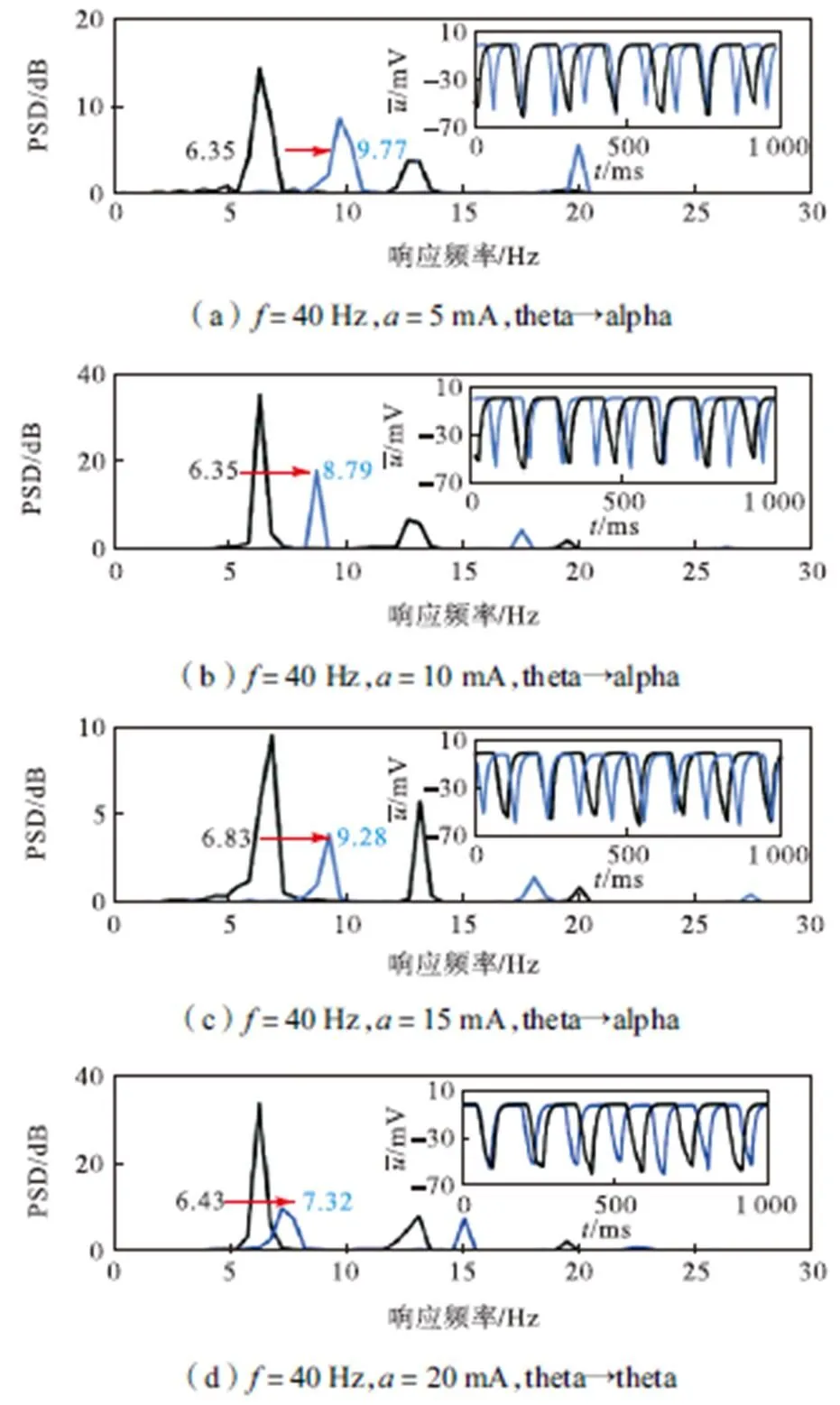
图7 PID控制调制

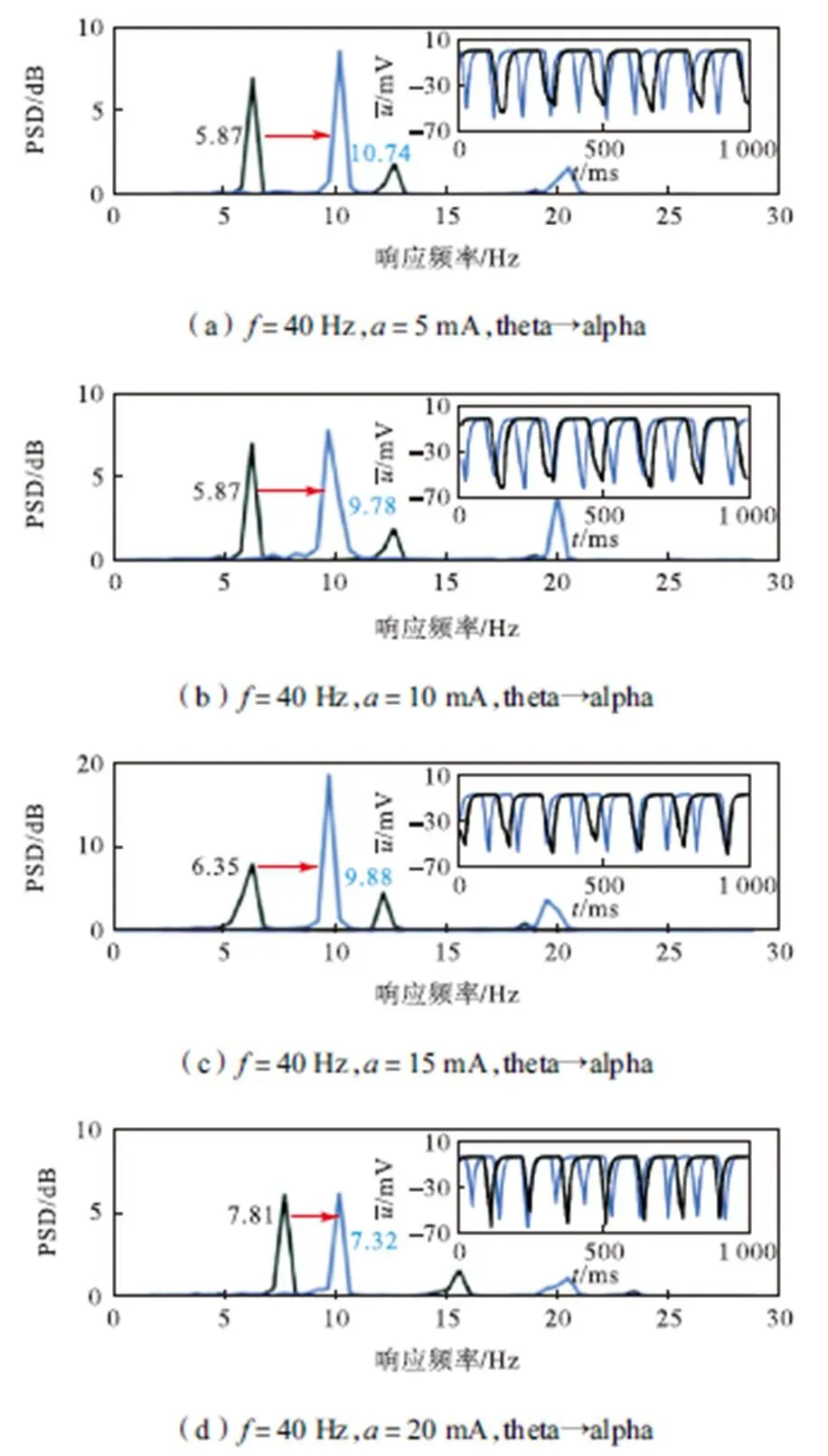
图8 PID型迭代控制调制图

2.4 不同节律的闭环调制

PID型迭代学习控制已在上文中被证明能自适应将网络主频从theta节律调制到alpha节律．但上述数值仿真实验具有一定局限性，主要表现为网络主频限制在theta节律．为验证PID型迭代控制学习算法对任意主频的调制能力，通过设置使网络产生不同的主频，并使该主频处于不同的频带，对网络施加PID型迭代学习控制算法，验证该算法调制节律的 能力.

如图9(a)和(b)所示，首先验证处于同一节律频带的不同主频能否被调制到期望alpha节律频带．先通过设置网络参数，使网络产生两种不同主频值，分别为6.836Hz和6.792Hz，但这两个主频都处于theta频带．然后通过控制算法调制，结果表明这两种主频值均能被调制到alpha频带．最后笔者验证了大量位于theta频带的主频是否能被调制到alpha频带，证明所有主频都能被调制成功．实验结果表明，该算法能有效调制位于相同节律下的不同主频至期望节律频带．

为了验证PID型迭代学习控制算法对处于不同频带主频的调制能力，将皮层网络初始节律设置到处于delta、beta和gamma频带，再利用该算法调制相应的网络节律，验证调制效果．调制结果展示在图9(c)～(e)中，利用PID型迭代学习控制算法能将处于非alpha频带的主频调制到目标alpha频带，实现对网络节律的调制，该算法使网络具有更强的可控性．当网络初始主频处于delta和theta频带时，调制的刺激幅值为正；当初始主频处于beta和gamma频带时，调制的刺激幅值为负．这些实验结果进一步验证了电刺激对皮层网络节律调制机制的不同．正幅值的脉冲刺激使网络主频增大，与之相反，负幅值的脉冲刺激使网络主频减小．综上所述，PID型迭代学习控制算法使节律的调制过程由繁变简，能调制任意初始节律到alpha节律.

2.5 PID型迭代学习控制律的收敛性证明

通过采用平均场理论简化理论推导过程，首先将单个神经元电势表示为平均场电位与噪声波动的共同作用为

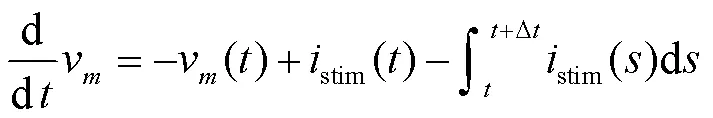
将式(1)的求和公式转化为积分公式，使该函数连续可积为

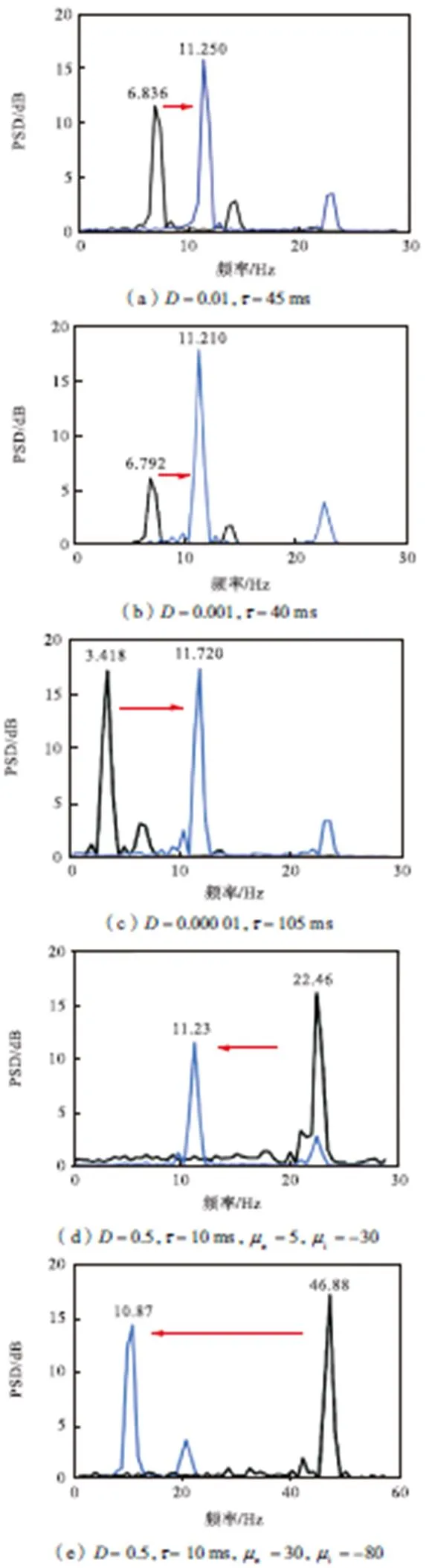
图9 节律调制图

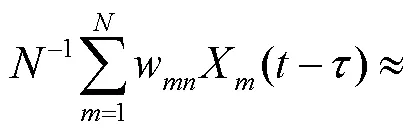
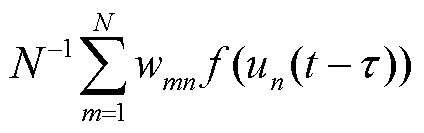
联立式(9)～式(11)计算得出平均场电位为

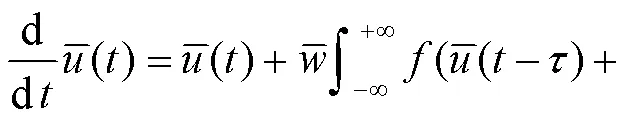
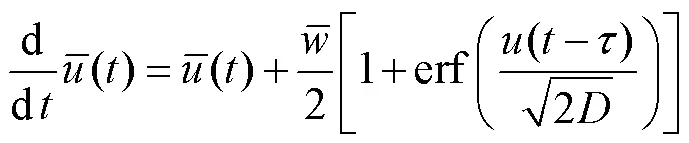
将式(15)转化为状态方程得

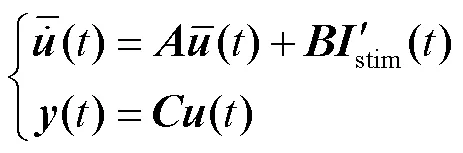
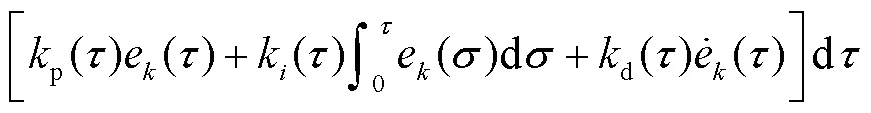
通过分部积分公式得

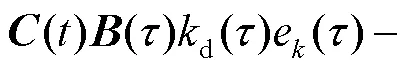
将式(18)的结果代入式(17)得

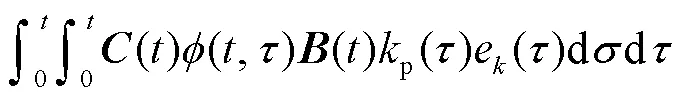
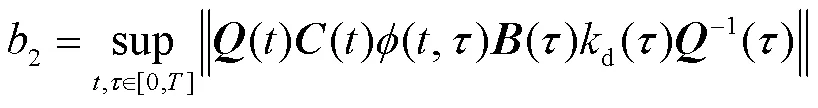
3 讨 论

为了达到实时自适应调制网络节律到期望节律的目的，本文设计了PID型迭代控制算法．由于模型中主要关注的是节律调控，因此使用较为简单的低阶模型，并在节律调制方面提供了合理的控制策略. PID型迭代学习控制算法能实时调制大脑节律，缩短电刺激参数调节时间，降低刺激能耗，实现自适应调制不同节律[21]．现阶段神经调制方法大部分是基于DBS技术，DBS调制已被证明在治疗脑疾病上有显著效果．通过在精确的作用靶点上对患者施加高频电刺激，能达到较好的治疗效果[22]．但是连续高频刺激具有一定缺陷，不但能耗高导致刺激装置续航能力差，而且高频刺激容易诱发众多的副作用．因此本文中选取的40Hz电刺激调制皮层网络节律，在大幅降低刺激能耗的基础上，有效调制了皮层节律．此外，已有实验研究证明40Hz光照刺激能有效调制小鼠网络节律活动，提高小鼠认知功能[23]．上述光照刺激为开环刺激，在此基础上添加PI控制调制光照刺激强度，进一步通过动物实验证明40Hz的闭环刺激能有效抑制癫痫疾病发作[24]．综上所述，相比于高频电刺激，40Hz电刺激的引入不但能减弱高频电刺激对大脑的强烈刺激作用和不适感，而且能大幅降低刺激能耗.

本文采用PID型迭代学习控制算法调制电刺激的幅值，调制过程中刺激的幅值主要表现为：随着迭代次数的增大，刺激幅值先随之降低，然后保持在较小的范围内呈现周期性变化．迭代学习控制通过迭代次数的增大，逐渐实现实际主频对期望主频的追踪．每次迭代的刺激幅值是由实际主频和期望主频做差，再通过迭代学习律计算所得，将该计算值作为下次迭代控制中的刺激幅值．仿真中每次迭代时间为1000ms，且在当次迭代中刺激幅值为定值，因此每次迭代过程中的刺激波形表现为重复性变化．随着迭代次数增大，实际主频与期望主频差值减小，导致刺激幅值减小，最终保持在一个较小数值．本文利用PID型迭代学习控制算法适用于重复性运动对象的优势，通过调制40Hz电刺激的幅值，能将不同的节律自适应调制到期望的alpha节律.

PID型迭代学习控制算法通过实时检测并计算皮层网络的平均场电位变化，自动调制电刺激的幅值．通过数学模型能更深入地分析闭环控制方法下刺激调制大脑节律的机制．但由于临床实验中存在多种环境阻抗因素，使得每个神经元受到不同的电刺激而非模型中的相同电刺激[25]，导致如果将该算法应用在实际中，调制的准确度可能会降低．此外，闭环控制方法中的反馈信号是实际主频值和期望主频值的差值，虽然该信号能有效表示大脑网络振荡活动，但是单一的反馈信号准确度和可靠性低于多个生物标记合成的反馈信号所具有的可靠性[26]．本文通过构建皮层网络平均场模型，在模型中验证闭环控制方法的可实施性，为皮层网络节律调制提供了有意义的分析和理论补充，但通过临床实验证明PID型迭代控制算法的有效性仍面临严峻的挑战.

4 结 语

目前通过闭环控制调制网络节律的方法仍不完善，为实现对皮层网络节律的自适应调制，本文构建了皮层网络振荡模型，通过PID型迭代学习控制调制皮层网络节律．利用功率谱密度分析计算相应频带的主频，计算真实主频和期望主频的差值，将该差值作为反馈变量，通过控制算法调制电刺激的幅值，进而达到自适应调制网络节律到alpha节律的目的．结果表明，PID型迭代学习控制能有效调制大脑节律，具有较强的鲁棒性，能将任意初始节律自适应调制到期望alpha节律．研究结果进一步从理论角度为临床中闭环电刺激的实施提供了补充，也为治疗多种节律活动异常的神经系统疾病提供了技术参考.

［1］ Klimesch W. EEG alpha and theta oscillations reflect cognitive and memory performance：A review and analysis[J]. Brain Research Review，1999，29(2)：169-195.

［2］ Scherberger H，Jarvis M R，Andersen R A. Cortical local field potential encodes movement intentions in the posterior parietal cortex[J]. Neuron，2005，46(2)：347-354.

［3］ Thut G，Miniussi C，Gross J. The functional importance of rhythmic activity in the brain[J]. Current Biology，2012，22(16)：R658-R663.

［4］ Abuhassan K，Coyle D，Maguire L. Compensating for thalamocortical synaptic loss in Alzheimer’s disease[J]. Frontiers in Computational Neuroscience，2014，8：65.

［5］ Bronstein J M，Tagliati M，Alterman R L. Deep brain stimulation for Parkinson disease an expert consensus and review of key issues[J]. Archives of Neurology，2011，68(2)：165-171.

［6］ Wang J X，Deng B，Gao T S，et al. Frequency-dependent response in cortical network with periodic electrical stimulation[J]. Chaos，2020，30(7)：073130.

［7］ Quinkert A W，Schiff N D，Pfaff D W. Temporal patterning of pulses during deep brain stimulation affects central nervous system arousal[J]. Behavioural Brain Research，2010，214(2)：377-385.

［8］ 任凯丽. 癫痫样放电状态建模与控制的研究[D]. 天津：天津大学精密仪器与光电子工程学院，2015.

Ren Kaili. The Modeling and Control of Epileptic Discharge State[D]. Tianjin：School of Precision Instrument and Opto-Electronics Engineering，Tianjin University，2015(in Chinese).

［9］ Santaniello S，Fiengo G，Glielmo L，et al. Closed-loop control of deep brain stimulation：A simulation study[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering，2011，19(1)：15-24.

［10］ 胡振华，封洲燕，郑晓静，等. 实时癫痫电位检测与闭环式电刺激系统的设计[J]. 生物医学工程学杂志，2015，32(1)：168-174.

Hu Zhenhua，Feng Zhouyan，Zheng Xiaojing，et al. Design of a system for real-time seizure detection and closed-loop electrical stimulation[J]. Journal of Biomedical Engineering，2015，32(1)：168-174(in Chinese).

［11］ Wang X J. Neurophysiological and computational principles of cortical rhythms in cognition[J]. Physiological Reviews，2010，90(3)：1195-1268.

［12］ 孙明轩，黄宝健. 迭代学习控制[M]. 北京：国防工业出版社，1999.

Sun Mingxuan，Huang Baojian. Iterative Learning Control[M]. Beijing：National Defence Industry Press，1999(in Chinese).

［13］ 李树楠，李冬辉，王 江. 神经元网络场电位的迭代学习控制研究[J]. 计算机应用研究，2016，33(3)：696-700.

Li Shunan，Li Donghui，Wang Jiang. Iterative learning control of field potential of neuronal network[J]. Application Research of Computers，2016，33(3)：696-700(in Chinese).

［14］ 张丽媛. 基于闭环控制的神经元及集群癫痫状态的研究[D]. 天津：天津大学精密仪器与光电子工程学院，2014.

Zhang Liyuan. Research on the Closed-loop Control of the Neuron and Neural Mass’s Epileptic State[D]. Tianjin：School of Precision Instrument and Opto-Electronics Engineering，Tianjin University，2014(in Chinese).

［15］ Li Shunan，Li Donghui，Wang Jiang，et al. Iterative learning control algorithm for spiking behavior of neuron model[J]. International Journal of Modern Physics B，2015，30(1)：1550240.

［16］ 曹玉珍，张丽媛，刘 晨，等. 基于Pinsky-Rinzel模型癫痫状态的估计与闭环混合[J]. 纳米技术与精密工程，2015，13(3)：232-238.

Cao Yuzhen，Zhang Liyuan，Liu Chen，et al. Estimation and closed-loop mixed control of epileptic state based on Pinsky-Rinzel model[J]. Nanotechnology and Precision Engineering，2015，13(3)：232-238(in Chinese).

［17］ Hutt A，Mierau A，Lefebvre J. Dynamic control of synchronous activity in networks of spiking neurons[J]. PLoS One，2016，11(9)：e0161488.

［18］ Liu C，Wang J，Li H，et al. Model-based iterative learning control of Parkinsonian state in thalamic relay neuron[J]. Communications in Nonlinear Science and Numerical Simulation，2014，19(9)：3255-3266.

［19］ Selvaraj P，Sleigh J W，Kirsch H E，et al. Closed-loop feedback control and bifurcation analysis of epileptiform activity via optogenetic stimulation in a mathematical model of human cortex[J]. Physical Review E，2016，93(1)：012416.

［20］ Rolls E T. Attractor networks[J]. Wiley Interdisciplinary Reviews-Cognitive Science，2010，1(1)：119-134.

［21］ Ortega J M，Rheinboldt W C. Iterative Solution of Nonlinear Equations in Several Variables[M]. New York：Society for Industrial and Applied Mathematics，1987.

［22］ 张建国，马 羽，刘焕光. 脑深部电刺激术在中国的发展现状[J]. 中国神经精神疾病杂志，2009，35(7)：385-387.

Zhang Jianguo，Ma Yu，Liu Huanguang. Development status of deep brain stimulation in China[J]. Chinese Journal of Neuropsychiatric Disorders，2009，35(7)：385-387(in Chinese).

［23］ Iaccarino H F，Singer A C，Martorell A J，et al. Gamma frequency entrainment attenuates amyloid load and modifies microglia[J]. Nature，2016，562 (7725)：E1.

［24］ Paz J T，Davidson T J，Frechette E S，et al. Closed-loop optogenetic control of thalamus as a tool for interrupting seizures after cortical injury[J]. Nature Neuroscience，2013，16(1)：64-98.

［25］ Zhang T，Grill W M. Effect of electrode geometry on deep brain stimulation：Monopolar point source[J]. IFMBE Proceedings，2009，24：167-170.

［26］ Giannicola G，Rosa M，Servello D，et al. Subthalamic local field potentials after seven-year deep brain stimulation in Parkinson’s disease[J]. Experimental Neurology，2012，237(2)：312-317.

Cortical Network Rhythm Modulation Based on the PID-Type Iterative Learning Control Algorithm

Wang Jixuan，Deng Bin，Wang Jiang，Yi Guosheng

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

The cortical network rhythm is a ubiquitous feature of brain dynamics closely related to cognitive and memory function. Abnormal brain rhythms cause certain disorders，such as epilepsy and Parkinson’s disease. Electrical stimulation could effectively modulate abnormal brain rhythms and further relieve the symptoms of diseases. The open-loop electrical modulation is a common method with high energy consumption，which has no feedback resulting in individual modulation difficulty. To realize the adaptive modulation of cortical rhythms，a mean-field model of the cortical network rhythm is proposed to generate spontaneous oscillation activities with different rhythms. First，the difference of the actual and desired dominant frequencies processed by the proportional-integral-derivative(PID)-type learning control law is taken as the feedback variables. The PID-type iterative learning control(ILC)algorithm is adopted to adaptively modulate the amplitude of 40Hz electrical stimulation. Modulating the dominant frequency from the theta rhythm to the alpha rhythm is realized. Next，the rhythms of the same and different individuals are modulated using the open-loop control，PID control，and PID-type ILC. The results prove that the PID-type ILC algorithm has the best individual modulation effect. The numerical simulation demonstrates that the algorithm could modulate arbitrary dominant frequencies in the delta，theta，and gamma rhythms to the alpha rhythm. Finally，the convergence of the algorithm is theoretically analyzed，which proves its effectiveness. Both theoretical derivation and numerical simulation have proven that the PID-type ILC algorithm could modulate the cortical rhythm to the alpha rhythm effectively by controlling the electrical stimulation amplitude，which presents a good individual modulation result. These results provide methodological guidance for the clinical treatment of abnormal rhythm diseases through closed-loop control.

rhythm modulation；cortical network；iterative learning control；closed-loop control

Q612

A

0493-2137(2022)10-1071-11

10.11784/tdxbz202109044

2021-09-28；

2021-12-08.

王佶宣（1995— ），女，博士研究生，wangjixuan@tju.edu.cn.

伊国胜，guoshengyi@tju.edu.cn.

国家自然科学基金资助项目(62071324)；天津市自然科学基金资助项目(19JCQNJC01200).

the National Natural Science Foundation of China(No. 62071324)，the Natural Science Foundation of Tianjin，China (No. 19JCQNJC01200).

(责任编辑：孙立华)