基于LTC-RNN模型的中长期电力负荷预测方法

邓 斌，张 楠，王 江，葛磊蛟

基于LTC-RNN模型的中长期电力负荷预测方法

邓 斌，张 楠，王 江，葛磊蛟

(天津大学电气自动化与信息工程学院，天津 300072)

针对中长期电力负荷预测受限于天气、温度、节假日等多重不确定性因素影响而精度不高的难题，本文采用一种基于液体时间常数的递归神经网络，实现了中长期电力负荷的精准预测，为电力系统规划设计奠定较好基础．基于液体时间常数的递归神经网络使用膜积分器改进了神经元的状态方程，并使用半隐式欧拉算法完成对神经元状态迭代更新，解决递归神经网络的自我修正能力弱和易陷入局部最优的问题．本文以天气、温度、节假日等外在影响因素作为网络输入，构建了以递归神经网络为基础架构的中长期电力负荷预测模型，并通过隐藏层的扩展计算获得输入-输出的映射关系，以通过时间的反向传播算法实现对模型的训练，完成对神经网络参数的优化．实验中，以北方某地区的实际电网数据为例，验证该预测方法的准确性与高效性．研究结果发现，基于液体时间常数的递归神经网络对中长期电力负荷的预测准确率可达到95.3%．本模型相较于长短期记忆和连续时间递归神经网络具有更稳定的训练结果与更高的预测准确度．

中长期电力负荷预测；递归神经网络；电力系统

在当今的电力系统中，科学的电力负荷预测能为合理的规划设计提供重要的基础数据．其中，精准的中长期电力负荷预测可以为系统管理、用电机组启停、发电机组维护等计划提供指导性的依据[1]．但是，中长期电力负荷不仅会受到节假日的影响，还会受到当日的温度、天气等不确定性因素的影响，是具有随机性的非线性时间序列[2]．因此，设计一种精准、高效的中长期电力负荷预测方法非常有必要，值得深入研究．

中长期电力负荷预测方法主要包括基于统计策略的传统预测方法与基于机器学习的现代智能方 法[3]．在诸多传统负荷预测方法中，回归分析法作为经典方法之一，是通过电力负荷的历史数据来寻找规律，预测未来的电荷数据．但这种方法一方面无法周全地考虑各种不确定性因素造成的影响，另一方面模型的参数初始化也难以实现[4]．现代智能方法在预测非线性电力负荷序列时，表现出了优于传统预测方法的性能．其中，Kandil等[5]构建了电力负荷的知识库，以较高的精度预测了长期电力负荷数据．但是这种专家系统方法难以实现自主学习，且数据库的构建十分困难．徐晶等[6]使用改进的支持向量机方法准确预测了短期商业电力负荷．但是在处理中长期电力负荷这种大规模数据时，支持向量机方法会出现训练时间过长、内存空间消耗过大的问题．

递归神经网络(recurrent neural network，RNN)及其改进模型具有拓扑结构可变和全节点权重共享的特点，易于学会非线性时间序列的内在规律，可以较好地实现对未来数据的预测．程换新等[7]使用粒子群算法改进的RNN成功预测了热电厂的短期电力负荷．但预测中长期电力负荷时，RNN会出现样本需求大和收敛速度慢等问题．长短期记忆(long short-term memory，LSTM)模型在RNN的神经元状态方程中引入了人脑的注意力机制，使得神经元上一时刻的状态成为当前时刻状态的组成部分，从而在样本较少的情况下实现了较为准确的电力负荷预测．但LSTM未充分利用隐藏层的历史状态，导致其在预测过程中对错误的修正能力较弱[8]．此外，连续时间RNN(continuous-time recurrent neural network，CTRNN)也广泛应用于非线性时序数据的预测领域．与LSTM不同的是，CTRNN仅使用3个神经元便实现了序列的生成，加快了模型的收敛速度．但是由于参与运算的神经元数目过少，CTRNN十分容易陷入局部最优[9]．为了解决LSTM自我修正能力弱和CTRNN易陷入局部最优的问题，本文寻求一种更优的改进方案完成对中长期电力负荷的精准预测．

Ramin等[10]根据对神经动力学的数理研究，改进了RNN隐藏层神经元的状态方程，构建了液体时间常数神经元与基于液体时间常数的递归神经网络(liquid time constant-recurrent neural network，LTC-RNN)．LTC-RNN具有较强的自我修正能力和寻找全局最优解的能力．首先，LTC-RNN使用半隐式欧拉方法计算了液体时间常数神经元的常微分方程(ordinary differential equation，ODE)．在计算过程中，神经元过去的状态会参与当前状态的计算，从而增强网络的自我修正能力和寻找全局最优解的能力．此外，LTC-RNN使用通过时间的反向传播(back propagation through time，BPTT)算法完成训练，通过优化网络的参数实现对中长期电力负荷数据内在规律的学习．LTC-RNN在解决天气条件影响下的车流量预测、温度影响下的臭氧含量预测、节假日影响下的房间占用率预测等预测问题时[11]，占用的内存空间较少，且预测的准确率较高．

基于以上问题，本文以天气、温度、节假日等外在影响因素作为网络输入，以电力负荷数据作为网络输出，采用LTC-RNN构建了中长期电力负荷预测模型．进一步，使用北方某地区电力系统的中长期电荷数据验证了该模型的预测高效性与准确性．最后，对比了同等规模LSTM和CTRNN的预测效果，证明LTC-RNN具有较强的稳定性，能产生更准确的预测结果．

1 RNN结构与模型

以预测的时间长度作为划分标准，一年或者几年的电力负荷可以称为中长期电力负荷．中长期电力负荷的预测结果有助于发电部门制定电力系统的计划．但是，由于需要预测的时间跨度较大，影响中长期电力负荷的不确定性因素也会更多．因此，在实现中长期电力负荷预测时，需要全面考虑包括天气、温度、节假日在内的多种影响因素．

RNN是一类通过状态反馈机制来学习时序数据内在动力学的人工神经网络．因此，RNN可以较好地构建从条件数据到记录数据的映射．即将条件数据输入给RNN，就可以输出该条件对应下的电荷数据．根据此功能，在解决多条件影响下的时序数据预测问题时，RNN获得了广泛的应用．于是本文基于RNN的网络结构，实现了对天气、温度、节假日等影响因素下，中长期电力负荷的预测．

典型的RNN结构使用输入层接收外界的输入数据，利用隐藏层神经元的状态来编码时序数据的内在规律，采用输出层产生预测的数据．RNN在训练的过程中，能将隐藏层神经元的状态按照运算的阶段实现展开，本文构建的RNN结构见图1．

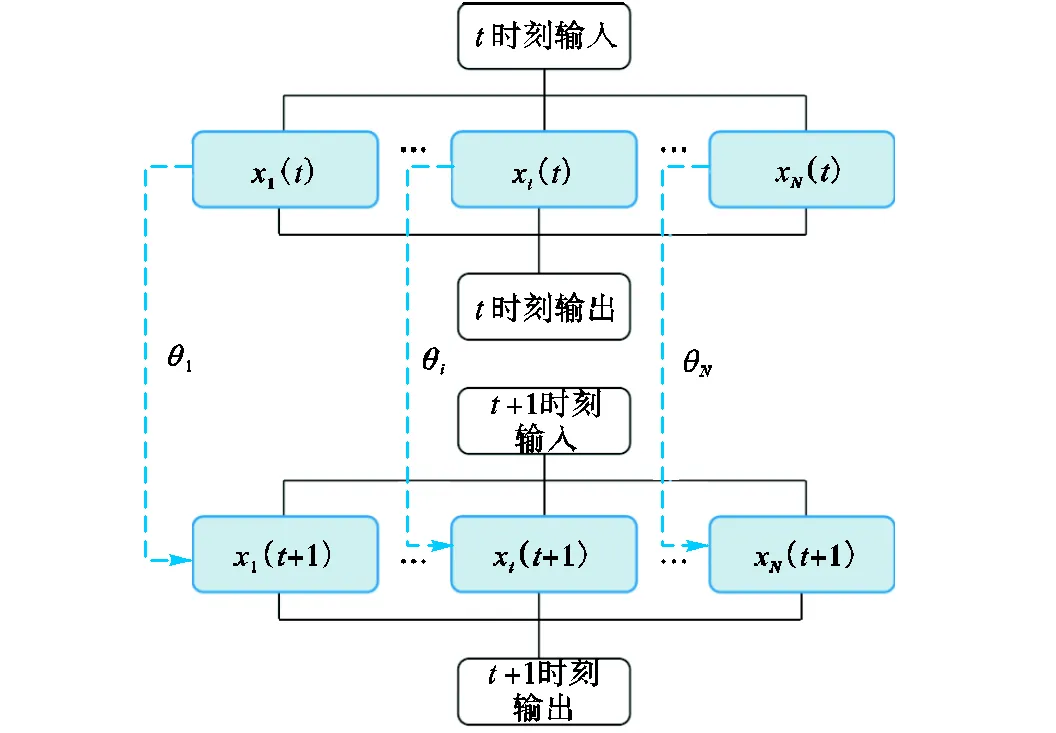
图1 RNN结构

在此，本文介绍了RNN的计算方程．RNN中神经元的状态能通过离散变换序列来定义，即

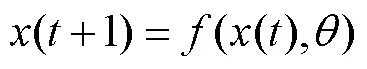
神经状态的离散化使得RNN在学习过程中能有效地接收误差，保证了训练的有效性．但是，状态离散化的有限性限制了神经元的表达能力．增加隐藏层的展开步骤可以有效地提高离散精度，但也会导致网络层数的增加，使得网络出现过量的计算，引起计算能力退化[12]．在此，通过向神经元的计算方程中增加过去状态的线性分量，以增强RNN的计算能力．于是获得神经ODE的离散方程如下.

根据ODE的欧拉离散化方式能将式(2)转换为连续方程[13]，即

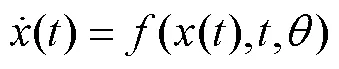
2 中长期电力负荷预测模型

使用RNN实现对中长期电力负荷的预测时，会出现数据需求量过大和收敛速度过慢的问题．因此，需要改进RNN的神经元状态方程，以提高网络的计算能力．但是，现今比较流行的LSTM对神经元历史状态的利用不足，导致该模型的自我修正能力较弱．而CTRNN在训练过程中参与计算的神经元较少，容易陷入局部最优．为解决这些问题，本文构建了具有较强自我修正能力和全局最优解寻找能力的LTC-RNN，以实现对中长期电力负荷的精准预测．

2.1 LTC-RNN模型

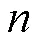
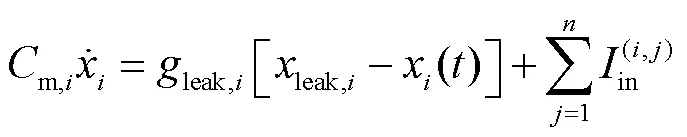
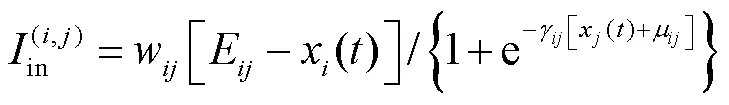
进一步，根据式(9)可以获得能够表示神经系统非线性动力学的时间常数为

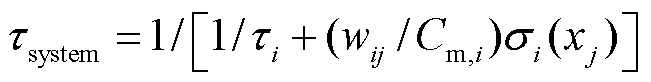
该非线性时间常数使得RNN隐藏层中的每个神经元都能识别输入所具有的动力学特征．根据这个特性，将该神经元模型构建的网络称为液体时间常数递归神经网络．

液体时间常数神经元以膜积分器模型为基础，充分考虑了突触电流、膜电容、漏电导等自然调节因素，放宽了神经ODE施加的限制，使得模型内的控制参数可以形成因果结构，以此提高神经网络的表达能力，使得LTC-RNN能够更好地学习中长期电力负荷的内在规律．

2.2 基于半隐式欧拉算法的状态求解

LTC-RNN的隐藏层神经元状态可以使用任意的常微分方程求解器来完成计算．为了加快LTC神经元状态的计算过程，本文使用半隐式欧拉方法来实 现状态求解，并给出该混合求解器下的神经元状态 方程．

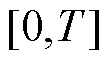
接下来，本文用式(3)来探讨显式欧拉方法与隐式欧拉方法在求解过程中所具备的优点与缺点．

显式欧拉方法将式(3)等号右侧变为斜率方程来实现求解，即

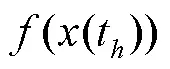
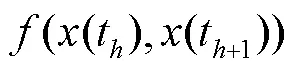
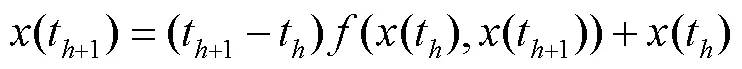
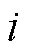
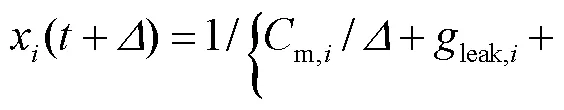
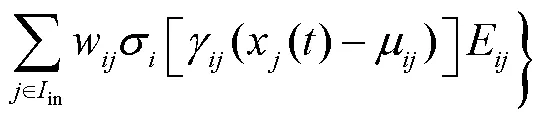
图3 LTC神经元结构

2.3 LTC-RNN的训练流程

已有研究表明，电力系统的负荷会受到包括人为因素、气象因素等多种不确定性因素的影响，进而产生随机的波动[14]．因此，在选择模型输入时，应全面地考虑能对电力负荷造成影响的因素，以提高预测模型的精确度．

根据对影响电力负荷波动的因素研究[15-16]，本文共整理出7个关键变量：①是否为法定节假日；②是否为工作日；③记录电荷的时刻(年/月/日，时/分/秒)；④温度(℃)；⑤云覆盖量(%)；⑥降雨量(mL)；⑦降雪量(mL)．

在训练之前，需要使用归一化方法将输入的训练负荷数据整合在(－1，1)的区间内，以方便模型的训练．归一化方法的计算公式为

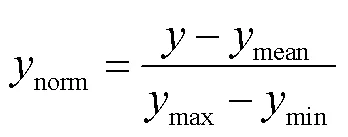
此外，还需对所选取的7种影响因素对应的时序数据进行预处理．其中，输入的温度、降雨量、降雪量和云覆盖量按照式(15)所示的归一化方法进行处理．对于记录的时间数据则根据具体的日期辨识是否为工作日或法定节假日，并使用二值序列来描述．

根据式(14)获得的LTC神经元结构，本文使用网络连接权重将32个LTC神经元连接起来，构建能够预测中长期电力负荷的LTC-RNN，其结构如图4所示．网络的输入会同时传递给网络中的每一个神经元，每个神经元的状态与对应的权重完成卷积，在卷积结果的基础上增加常数偏置，最终获得网络的输出．本文使用BPTT算法来训练网络，即根据网络输出与实际数据的误差调整模型的连接权重，使得网络能够实现输入-输出的映射关系．

图4 LTC神经元网络结构

基于LTC-RNN构建的中长期电力负荷预测模型的训练流程如图5所示．首先需要收集数据，收集的数据包括电力负荷数据、当日节假日情况、当日温度数据、当日气象数据．从收集到的数据中提取需要传入给LTC-RNN的关键影响因素，并进行预处理．对于处理后的多组数据，按照20∶3∶1将数据划分为训练集、验证集和测试集．在网络训练之前使用高斯随机分布对网络的权值进行初始化，并采用Adam算法完成对网络连接权值的更新．训练过程中，利用训练集的误差来进行反传，使用验证集的误差防止模型出现过拟合．训练结束后，使用测试集验证模型的训练效果．

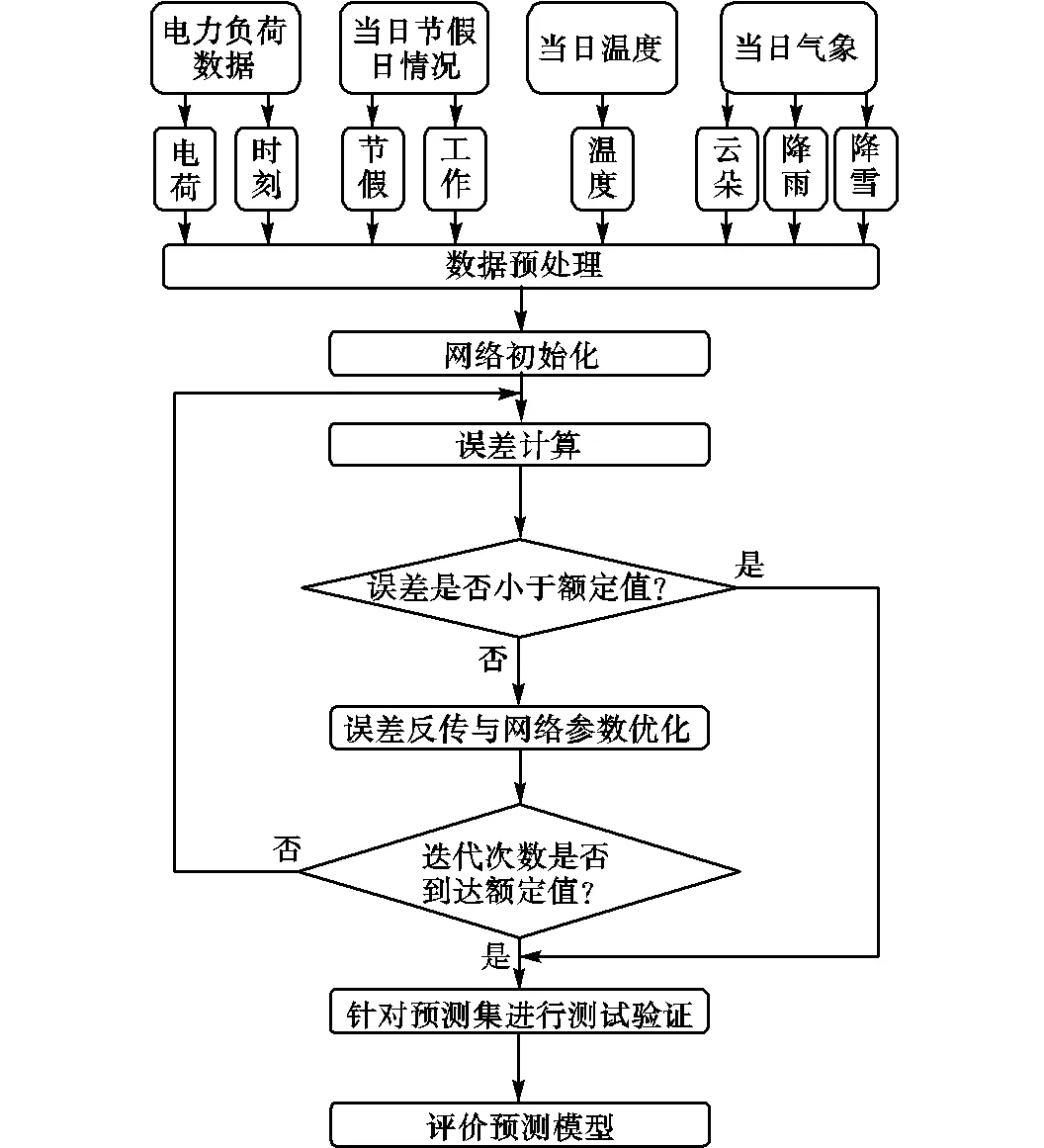
图5 LTC-RNN训练流程

3 案例分析

3.1 基础数据集

本文使用我国北部某地区的实际电网数据实现对LTC-RNN预测效果的验证．该数据记录了某年12月到次年12月的数据，数据包含每天整点时刻的电力负荷实际值，完成了共计8784组条件数据以及电荷数据的采集．

本文涉及到的LSTM、CTRNN以及LTC-RNN电力负荷预测模型均在Python下完成搭建．

3.2 评价指标

为了测试该模型中长期电力负荷的训练与预测效果，本文按照20∶3∶1将数据划分为训练集、验证集和测试集．在这里选择每天12：00时的测试条件与电力负荷值作为测试数据集．

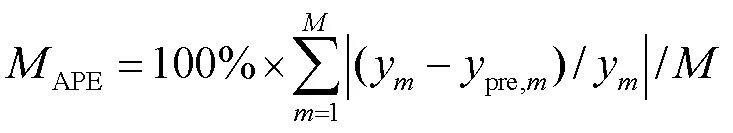
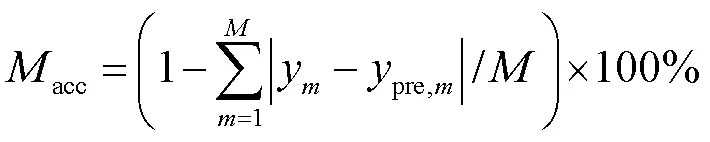
3.3 实验结果分析

图6(a)所示的LTC-RNN对测试数据集的预测结果表明，该模型可以比较准确地预测出一年内电力负荷的变化趋势．图6(a)中浅灰色曲线表示训练数据集在一年内的变化趋势，虚线表示测试数据集的电力负荷数据，黑色实线表示LTC-RNN预测获得的电力负荷数据．该北方数据反映出，在3—4月份电力负荷会出现明显的下降，而在11月份会出现显著的上升．这种显著的变化趋势可能与北方1—3月份、11—12月份天气比较寒冷，且日照时间较短有关，更多的电能被用于取暖与照明，导致电力负荷的消耗较大．LTC-RNN模型的预测结果表明，该模型能够较好地预测出这一年内电力负荷的变化趋势．

此外，本文还使用了同等规模的LSTM和CTRNN对相同的电力负荷数据集进行了训练，来对比这几种改进RNN的预测能力．根据图6(b)和6(c)中预测结果可以看出，LSTM和CTRNN可以较好地预测出较平稳的电力负荷趋势，但是对于3—4月份与11月份出现的大幅度变化却无法做出准确的预测．由此可见，LTC-RNN可以很好地预测多种不确定性因素影响下的中长期电力负荷变化趋势，其预测准确度明显优于LSTM和CTRNN．

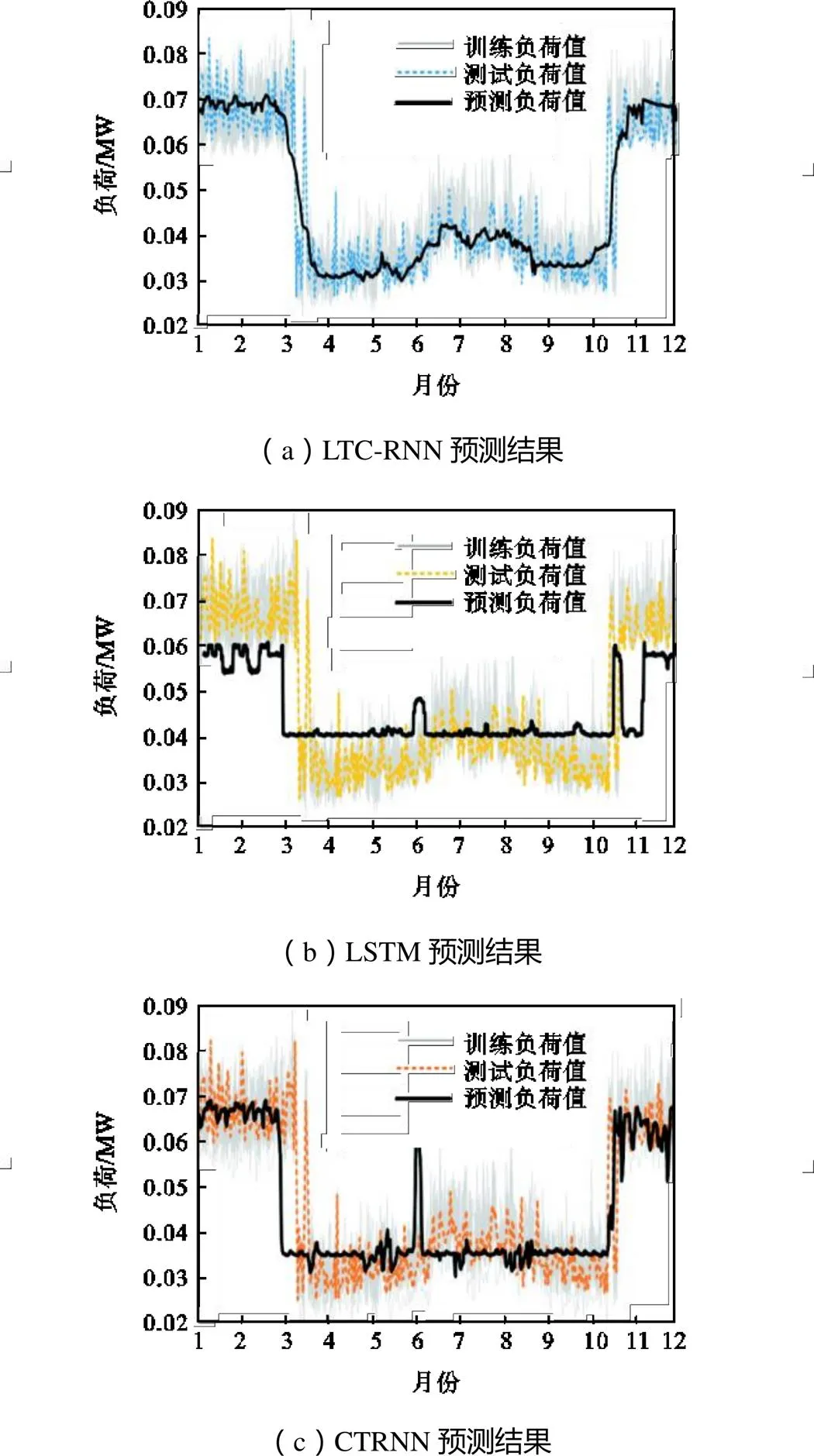
图6 对某年电力负荷进行预测的结果

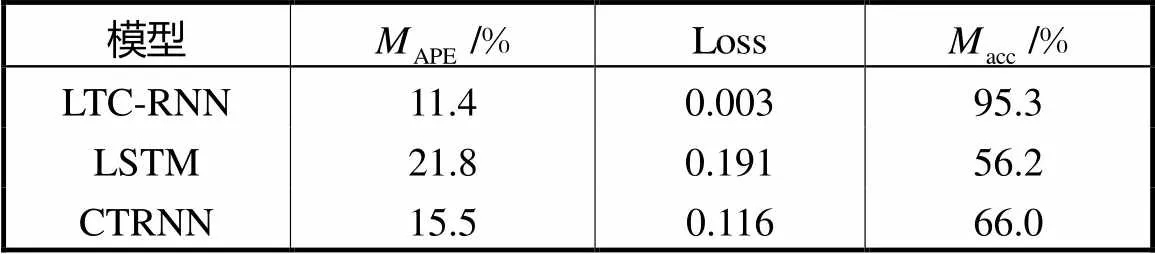
表1 中长期负荷预测模型评价

最后，本文对比了3种模型在训练过程中的模型损失和准确度．根据图7(a)所示，在训练的过程中，LTC-RNN、LSTM、CTRNN的验证集损失可以准确地跟随训练集的损失，这说明3种模型在计算过程中未出现过拟合现象．但是LSTM的损失曲线在训练过程中出现了明显的大幅波动，这说明LSTM的训练过程极不稳定．而LTC-RNN和CTRNN的损失曲线都出现了持续下降的趋势，且LTC-RNN在快速下降后到达了稳定状态，这说明LTC-RNN的训练过程收敛速度较快，收敛后的稳定性较好．图7(b)则对比了3种模型对于测试集的预测准确度．图7(b)中可以发现，LTC-RNN可以在极短的训练回合内到达90%以上的准确度，LSTM与CTRNN在相同的时间只能达到60%左右的准确度，表明LTC-RNN在计算的效率方面更具优势．此外，在整个训练过程中，LTC-RNN在到达一定的准确度后，曲线的上升趋势变缓，准确率的增加幅度明显降低．CTRNN的准确度曲线一直处于上升阶段，LSTM的准确度曲线在到达一定高度时出现了明显的波动．这说明LTC-RNN可以在较短的训练过程中得到全局最优解，其稳定性明显优于LSTM与CTRNN．

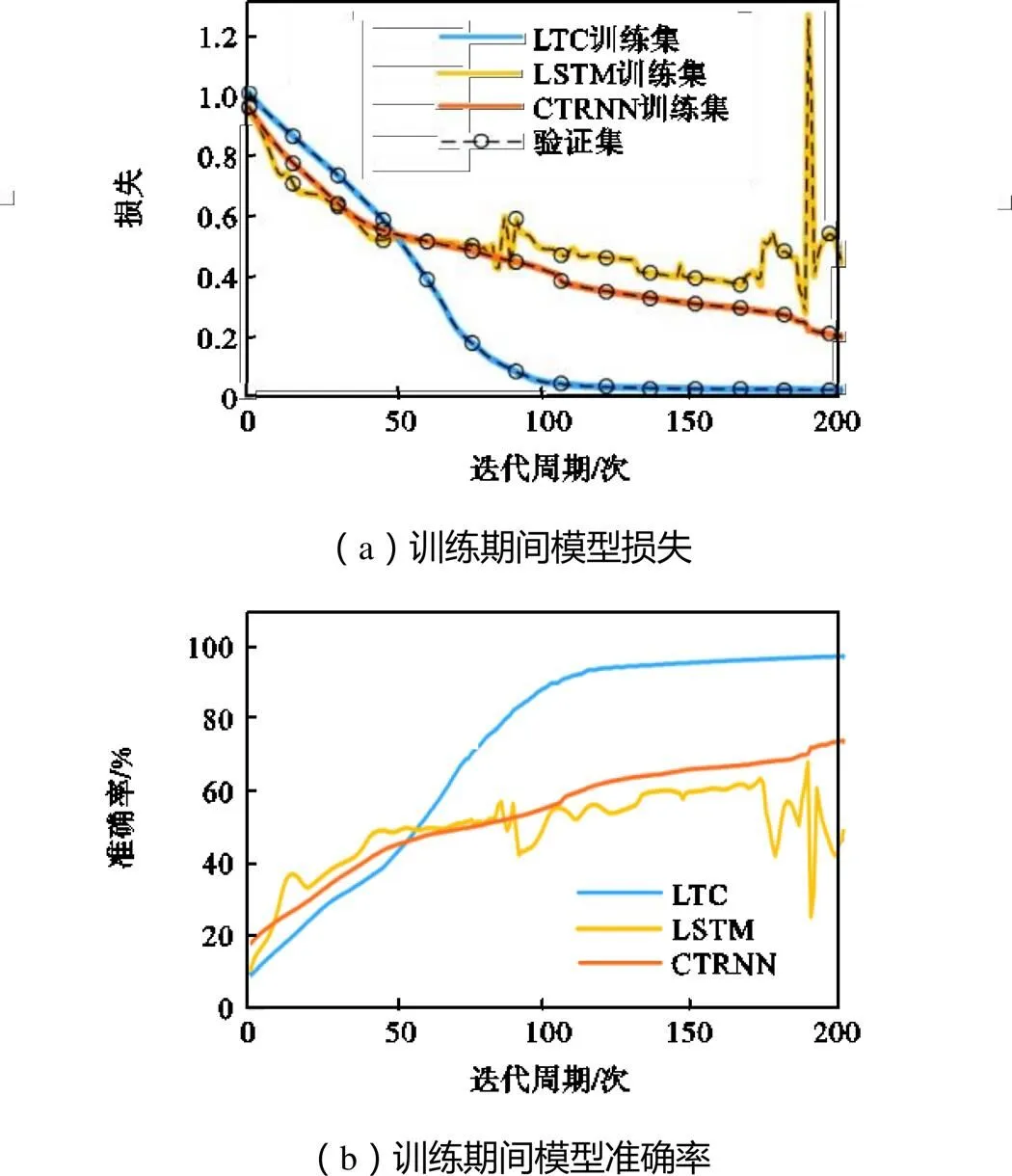
图7 负荷预测模型评价

4 结 论

在当今的电力系统规划设计中，发电系统的维护、发电机组的分配安排、增容维护等，都需要科学的中长期电力负荷的预测来提供数据支持．于是，本文采用LTC-RNN构建了中长期电力负荷的预测模型，能够精准预测受天气、温度、节假日等不确定性因素影响的电网负荷．并使用北方某地区电网的实际电力负荷验证了该方法的准确性与高效性．依据本文的研究可得到结论如下．

(1) LTC-RNN以膜积分器为参考，改进了RNN神经元的状态方程，利用神经元的历史状态计算隐藏层神经元的状态，增强了模型的自我修正能力．本文对实际案例的分析证实，LTC-RNN可以快速稳定地到达最优参数，具有计算的高效性．

(2) LTC-RNN采用半隐式欧拉求解器计算隐藏层神经元状态，使得模型易于寻找到全局最优解．本文对实际案例的预测结果证实，LTC-RNN可以精确地预测电网的中长期电力负荷．

(3) LTC-RNN充分学习了天气、温度、节假日等不确定性因素与中长期电力负荷的内在联系．根据影响因素的数据，LTC-RNN可以准确地预测出对应的电力负荷．本文中的案例中，该模型对中长期电力负荷的预测准确率可达95.3%，优于LSTM和CTRNN的预测效果．

在此指出，对该模型的验证主要使用了北方某地区的电力系统数据，未来考虑将LTC-RNN应用于更多具有不同负荷变化趋势的地区，以此来验证该模型的广泛应用效果．

［1］ Lindberg K B，Seljom P，Madsen H，et al. Long-term electricity load forecasting：Current and future trends[J]. Utilities Policy，2019，58：102-119.

［2］ 徐宪东，单文亮，蔡云帆，等. 流程工业综合能源系统用电灵活性综述[J]. 天津大学学报(自然科学与工程技术版)，2021，54(12)：1212-1220.

Xu Xiandong，Shan Wenliang，Cai Yunfan，et al. A perspective on electricity flexibility of integrated energy systems in processing industries[J]. Journal of Tianjin University(Science and Technology)，2021，54(12)：1212-1220(in Chinese).

［3］ 张 志，杜延菱，崔慧军，等. 考虑关联因素的智能化中长期电力负荷预测方法[J]. 电力系统保护与控制，2019，47(2)：24-35.

Zhang Zhi，Du Yanling，Cui Huijun，et al. Intelligent mid-long electricity load forecast method considering associated factors[J]. Power System Protection and Control，2019，47(2)：24-35(in Chinese).

［4］ 夏 博，杨 超，李 冲. 电力系统短期负荷预测方法研究综述[J]. 电力大数据，2018，21(7)：22-28.

Xia Bo，Yang Chao，Li Chong. Review of the short-term load forcasting methods of electric power system[J]. Power Systems and Big Data，2018，21(7)：22-28(in Chinese).

［5］ Kandil M S，Debeiky S M，Hasanien N E. The implementation of long-term forecasting strategies using ac-knowledge-based expert system[J]. Electric Power Sys-tem Research，2001，58(1)：19-25.

［6］ 徐 晶，迟福建，葛磊蛟，等. 基于SARIMA-GRNN-SVM的短期商业电力负荷组合预测方法[J]. 电力系统及其自动化学报，2020，32(2)：85-91.

Xu Jing，Chi Fujian，Ge Leijiao，et al. Short-term combined commercial load forecasting method based on SARIMA-GRNN-SVM[J]. Proceedings of the CSU-EPSA，2020，32(2)：85-91(in Chinese).

［7］ 程换新，黄 震. 基于改进PSO优化RNN的短期电力负荷预测模型[J]. 电子测量技术，2019，42(20)：94-98.

Cheng Huanxin，Huang Zhen. Short-term electric load forecasting method based on improved PSO optimized RNN[J]. Electronic Measurement Technology，2019，42(20)：94-98(in Chinese).

［8］ 葛磊蛟，刘航旭，赵 康，等. 面向商业和居民混合的配电网短期负荷预测HGWOACOA-LSTMN 方法[J]. 天津大学学报(自然科学与工程技术版)，2021，54(12)：1269-1279.

Ge Leijiao，Liu Hangxu，Zhao Kang，et al. An HGWOACOA-LSTMN method for short-term load fore-casting of distribution network for commercial and resi-dential users[J]. Journal of Tianjin University(Science and Technology)，2021，54(12)：1269-1279(in Chi-nese).

［9］ Henaff P，Scesa V，Ouezdou F B，et al. Real time implementation of CTRNN and BPTT algorithm to learn on-line biped robot balance：Experiments on the stand-ing posture[J]. Control Engineering Practice，2011，19(1)：89-99.

［10］ Ramin H，Mathias L，Alexander A，et al. Liquid time-constant networks[EB/OL]. https：//arxiv. org/abs/2006. 04439v2，2020-09-12.

［11］ Ramin H. Interpretable Recurrent Neural Networks In Continuous Time Control Environments[D]. Wien：Technische Universität Wien，2020.

［12］ 王超洋，张蓝宇，刘 铮，等. 基于特征挖掘的indRNN光伏发电功率预测[J]. 电力系统及其自动化学报，2021，33(4)：17-22.

Wang Chaoyang，Zhang Lanyu，Liu Zheng，et al. Fea-ture mining based indRNN photovoltaic power genera-tion prediction[J]. Proceedings of the CSU-EPSA，2021，33(4)：17-22(in Chinese).

［13］ 杨文强，吴文渊. 线性常微分方程的全局误差估计和优化求解方法[J]. 中国科学：数学，2021，51(1)：239-256.

Yang Wenqiang，Wu Wenyuan. Global error estimation for linear ordinary differential equations and their nu-merical optimal solutions[J]. Scientia Sinica：Mathematica，2021，51(1)：239-256(in Chinese).

［14］ 肖 峻，耿 芳，杜柏均，等. 基于关联规则的城市电力负荷预测模型智能推荐[J]. 天津大学学报，2010，43(12)：1079-1085.

Xiao Jun，Geng Fang，Du Bojun，et al. Intelligent recommendation of urban power load forecasting models based on association rules[J]. Journal of Tianjin Univer-sity，2010，43(12)：1079-1085(in Chinese).

［15］ 崔和瑞，彭 旭. 基于ARIMAX模型的夏季短期电力负荷预测[J]. 电力系统保护与控制，2015，43(4)：108-114.

Cui Herui，Peng Xu. Summer short-term load forcasting based on ARIMAX model[J]. Power System Protection and Control，2015，43(4)：108-114(in Chinese).

［16］ 张振高，杨正瓴. 短期负荷预测中的负荷求导法及天气因素的使用[J]. 电力系统及其自动化学报，2006，18(5)：79-83.

Zhang Zhengao，Yang Zhengling. Load derivation in short term forcasting using weather factor[J]. Proceed-ings of the CSU-EPSA，2006，18(5)：79-83(in Chi-nese).

Medium- and Long-Term Power Load Forecasting Method Based on LTC-RNN Model

Deng Bin，Zhang Nan，Wang Jiang，Ge Leijiao

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

Owing to various uncertainties，such as weather，temperature，and holidays，predicting long-term power load remains difficult. This paper introduces a liquid time constant-recurrent neural network to accurately predict medium- and long-term power load，which is the fundamental work for power system planning and design. The liquid time constant-recurrent neural network improves the equation of neural states and uses a semi-implicit Euler algorithm to complete the iterative updating of the neural states，which solves the problem that the recurrent neural network has poor self-correction ability and is prone to falling into local optimum. A recurrent neural network-based model for forecasting medium- and long-term power load is constructed using network inputs such as weather，temperature，and holidays. The mapping from input to output is then obtained using extended computation in hidden layers，and the parameters of the neural network are optimized using a time algorithm via backpropagation. Actual power grid data from a specific area in North China are used to validate the accuracy and efficiency of the proposed method. The experimental results show that the liquid time of the constant-recurrent neural network can reach 95.3% accuracy for predicting medium- and long-term power load. With better stability during training and higher accuracy in the prediction phase，this model outperforms the long short-term memory algorithm and continuous-time recurrent neural network.

medium- and long-term power load forecasting；recurrent neural network；power system

TK715

A

0493-2137(2022)10-1026-08

10.11784/tdxbz202112006

2021-12-03；

2022-02-20.

邓 斌（1979— ），男，博士，教授，dengbin@tju.edu.cn.

葛磊蛟，legendglj99@tju.edu.cn.

国家自然科学基金资助项目(51807134).

the National Natural Science Foundation of China(No. 51807134).

(责任编辑：孙立华)