改进型多用户高效DCSK通信方案的性能分析
2022-07-04董江涛张天骐吴雪霜
张 刚,董江涛,张天骐,吴雪霜
(重庆邮电大学 通信与信息工程学院,重庆 400065)
混沌的发现消除了拉普拉斯决定式可预测性的幻想,并与相对论、量子力学齐名为20世纪物理学最伟大的成就。混沌是由确定性系统内部随机性的影响,引起的一种复杂且看似无规则的运动。本质上,混沌不是真正的无序,更恰当地说是没有周期性的有序运动[1]。近些年来,混沌在通信系统中的运用最受全世界学者关注。混沌信号具有良好的类随机性、确定性和对初值极其敏感的特性,使混沌通信系统具有良好的保密性能。由于混沌信号的产生简单且成本较低,可以很好地代替传统载波,在扩频通信和保密通信中有很好的前景和实用价值[2-6]。
近二十年来,学者们提出了许多基于混沌的非相干通信方案。差分混沌移键控(Differential Chaos Shift Keying,DCSK)系统通过对数据进行采样,在连续的比特持续时间内重复或反转参考信号。该系统具有解调方式简单、接收端不需要载波同步和信道估计并且系统成本低等优点,且DCSK系统在对抗多径干扰时体现出出众的能力,所以在超宽带系统[7-8]、多入多出系统[9]等场景中对DCSK系统都有所运用。但DCSK系统使用传输参考技术[10-11]导致数据安全性能差且传输速率低,参考信号与信息信号分时隙传输也导致两个信号均受到噪声干扰,使得系统的误码率较高。
针对DCSK系统的缺点,诸多学者提出不同的改善方案。为了改善数据传输速率,文献[12]和文献[13]分别提出了相关延迟移位键控(Correlation Delay Shift Keying,CDSK)和正交混沌移位键控(Quadrature Chaos Shift Keying,QCSK)。但是,CDSK的参考信号和信息信号发送在一定的时间延迟中,在接收端会产生更多的干扰,在提升传输速率的同时降低了误码率性能;而QCSK使用希尔伯特变换产生正交基函数的成本相当高并且提升了系统复杂性。文献[14]引入了一种高效的DCSK (HE-DCSK)。在HE-DCSK中,通过在DCSK中增加一路时间延迟,可以在一个数据序列中携带2 bit数据,传输速率相较于DCSK系统提高了1倍。在HE-DCSK之后,杨华等又提出了基于无信号内干扰的HE-DCSK[15]。利用一个简单正交混沌信号发生器产生一组完全正交的混沌信号,再通过HE-DCSK系统,消除了信号之间的干扰,提高了HE-DCSK系统的误码性能。对于多用户系统,张刚等提出了诸多不同系统,在文献[16]中提出了正交多用户差分混沌移位键控系统(Orthogonal Multi-User Differential Chaotic Shift Keying,OMU-DCSK),为了提高多用户系统的误码性能,设计了一种与文献[15]不同的正交混沌信号发生器。该发生器将混沌信号源与Walsh码相结合,同时可以产生多路正交的混沌序列,彻底克服了多址干扰,有效降低了平均比特能量。文献[17]则提出了一种基于短参考信号下的多用户系统(Short Reference Multi-User Differential Chaos Shift Keying,SR-MUDCSK),利用Walsh码的正交特性传输多用户信息,有效地将短参混沌系统与多用户结合,大大提升了短参混沌系统的传输速率。文献[18]提出一种基于频分复用的无信号内干扰多用户系统(Multi-User Correlation Delay Shift Keying with no Intra-Signal Interference,NISI-MU-CDSK),首先由正交混沌信号发生器产生两个正交混沌信号,之后两个正交信号通过简单的线性组合产生两路参考信号,最后利用FDM技术传输两路参考信号以及多个用户信息信号,在系统误码性能和传输速率上均得到了提升。
改进型多用户高效DCSK(Improved Multi-User High-Efficiency Differential Chaos Shift Keying,IMU-HE-DCSK)系统改善了传统HE-DCSK系统中传输速率和误码性能的问题。在发送端利用正交混沌信号发生器产生两路正交信号,并通过加减的线性组合产生两路参考信号,之后两路参考信号与信息信号和Walsh码序列调制,传输多个用户信息且每个用户可同时传输4 bit信息比特,从而提高系统的传输速率,最后将两路信号进行正交调制。在接收端通过均值滤波器对部分接收信号进行降噪,降低系统误码率。笔者对IMU-HE-DCSK进行了理论公式推导和蒙特卡罗仿真分析,证明了IMU-HE-DCSK的可行性,为本系统应用于实际提供理论参考。
1 IMU-HE-DCSK方案原理
由于不同混沌信号之间的相关性无法彻底消除,使得判决变量中出现不同信号之间引起的干扰分量。笔者借鉴一种简单的正交混沌信号发生器(Orthogonal Chaotic signal Generator,OCG),生成两路严格正交的混沌信号,能够有效地抑制信号间干扰,如图1所示。
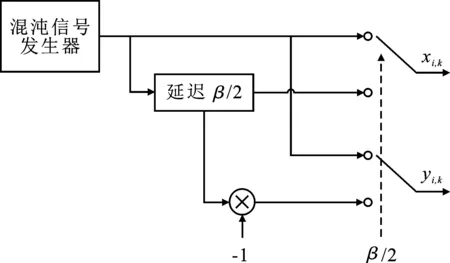
图1 正交混沌信号发生器(OCG)原理图
图1中,在正交混沌信号发生器内部,由混沌信号发生器产生一段长为β,带宽为500 MHz的混沌序列pi,k,其混沌序列pi,k的生成满足:
(1)
其中,k表示第k个数据帧;i=1,2,3,…,β;β为扩频因子,且2β=Tb/Tc,Tb为比特周期,Tc为码片周期。由式(1)可得,混沌序列pi,k的E[pi,k]=0,var[pi,k]=1。
首先,序列pi,k通过正交混沌信号发生器内部输出一组正交混沌序列xi,k,yi,k,其满足式(2)和式(3),即
(2)
(3)
在前β/2时隙内,输出序列xi,k和yi,k相同;在后β/2时隙内,输出序列xi,k和yi,k相反。在一个β内可得到一组正交的混沌序列xi,k,yi,k,其中,有E[xi,k]=E[yi,k]=0,var[xi,k]=var[yi,k]=1。
IMU-HE-DCSK发送第k帧信号的发送端结构框图如图2所示。
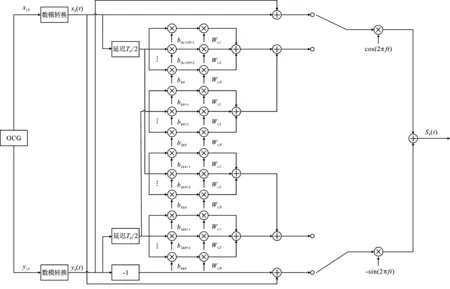
图2 IMU-HE-DCSK发射端框图
图2中Walsh码[19]序列实现区分不同的用户信息,其中,j=1,2,…,N,N为总用户数。Walsh码序列是通过Hadamard矩阵产生的,Hadamard矩阵是一种特殊的方阵,其元素全为“+1”或“-1”,且阶数是2的倍数。
由于矩阵中的任意一行或一列与其他行或列都是正交的,因此矩阵的每一行可当作一个Walsh码序列。Hadamard矩阵构造满足:
(4)
其中,n为阶数,每一行代表一个长度为2n的Walsh码。图2中首先利用正交混沌发生器得到一组长为β,带宽500 MHz的正交混沌序列xi,k,yi,k。再经数模转换后得到一组连续的模拟信号xk(t),yk(t)。
然后,分为两路发送不同的参考信号和信息信号。在第1路,xk(t)和yk(t)先相加作为参考信号在第1个时隙发送。然后xk(t)和yk(t)均延迟Tb/2后作为信息承载信号,延迟信号xk(t-Tb/2)与信息比特b(k-1)N+j和相应的Walsh码Wi,j相乘,作为每个用户的第1个信息信号;而yk(t-Tb/2)与信息比特bkN+j和相应Walsh码Wi,j相乘,作为每个用户的第2个信息信号。再将N个用户的前两个信息信号相加,作为总的信息信号在第2个时隙发送。第2路中,xk(t)和-yk(t)相加,作为参考信号在第1个时隙发送。第2个时隙与第一路大致相同,xk(t-Tb/2)与用户发送的第3个信息比特b2kN+j相乘,然后和相应的Walsh码Wi,j相乘,作为第3个信息信号;同样,yk(t-Tb/2)与用户发送的第4个信息比特b3kN+j相乘,之后与相应Walsh码Wi,j相乘,作为第4个信息信号。将N个用户的后两个信息信号相加,作为总的信息信号在第2个时隙发送。
最终,两路信号分别与载波cos(2πft)和-sin(2πft)进行调制,再将调制后的两路相加,作为第k帧的发送信号sk(t)输出,其中f是载波的频率。则IMU-HE-DCSK发送的第k帧信号sk(t)的表达式为
sk(t)=
(5)
由式(5)可得,发送信号sk(t)的平均比特能量为
(6)
图3是IMU-HE-DCSK第k帧第u(u∈j)个用户的接收端框图。
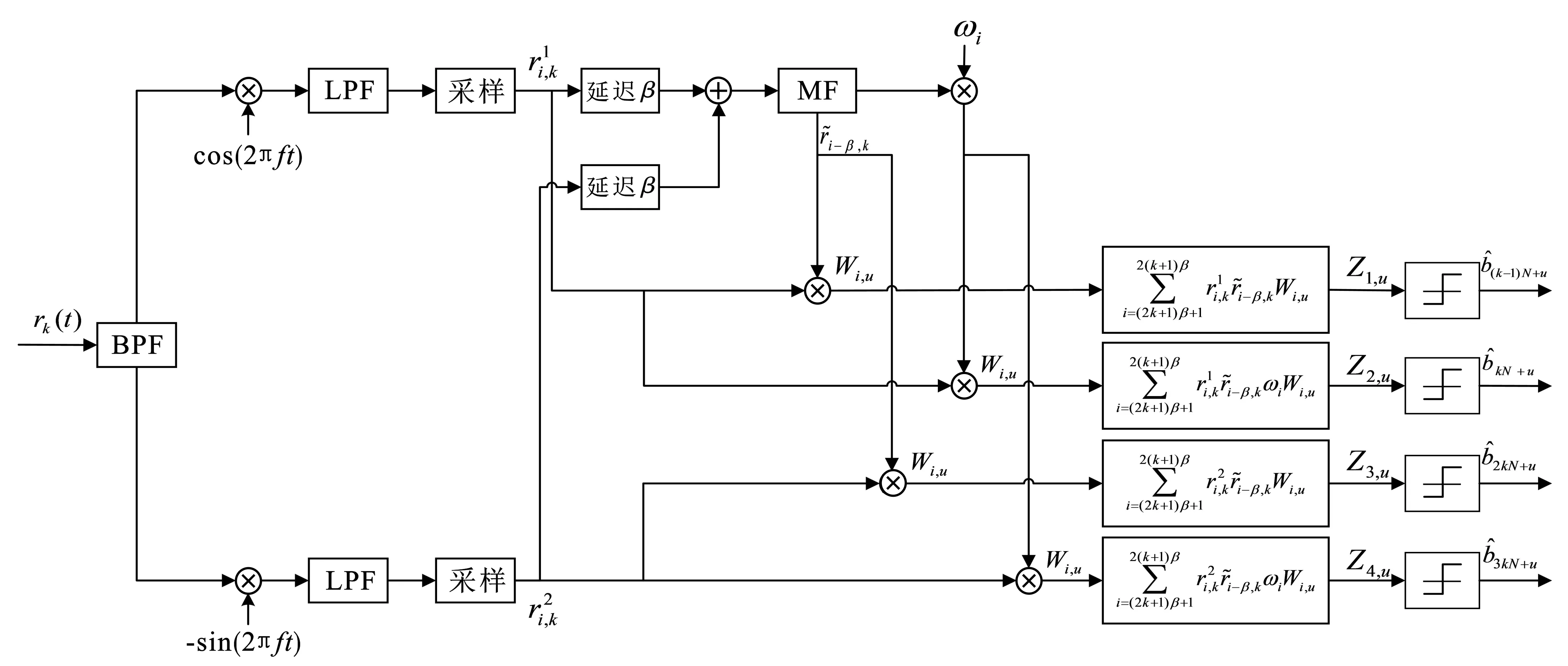
图3 IMU-HE-DCSK接收端框图
系统接收到的信号rk(t)通过一个中心频率为f的带通滤波器。再分别与载波cos(2πft)和-sin(2πft)相乘进行解调,解调后的信号通过一个低通滤波器并对其进行采样处理,其中采样间隔为Tb/(2β)。
(7)
瑞利衰落信道模型是无线通信中最常用的信道模型。因此文中主要分析IMU-HE-DCSK在多径瑞利衰落信道下的误码性能,信道模型如图4所示。假设发送信号在多径瑞利衰落信道中传输,传输过程中受加性高斯白噪声的干扰。其中,nk(t)代表加性高斯白噪声信号。

图4 多径瑞利衰落信道模型
当发送信号sk(t)经过图4信道后,到达接收端的信号rk(t)表示为
(8)
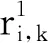
(9)
(10)
在接收端,第u个用户的相关器的4个输出分别为
(11)
(12)
(13)
(14)

(15)
2 IMU-HE-DCSK方案性能分析
2.1 BER性能分析
运用高斯近似法推导了多径瑞利衰落信道下IMU-HE-DCSK的理论BER。所有的理论推导是基于以下假设完成的:
(1) 作为加性高斯白噪声的干扰,当i≠j时,ni,k与nj,k之间相互独立;当取任意(i,j)时,ni,k与xj,k之间也是相互独立的,并有E[ni,k]=E[nj,k]=0,var[ni,k]=var[nj,k]=N0/2。
(2) 当扩频因子趋于无穷大时,判决变量中每一项都近似服从高斯分布。
(3) 系统发送的是二进制信息比特,且信息比特“+1”、“-1”等概率发送。
(4) Walsh码完美同步,其数学特性为
E[Wi,mWi,n]=E[Wi,m]=E[Wi,n]=0 ,
(16)
var[Wi,mWi,n]=var[Wi,m]=var[Wi,n]=1 。
(17)
由于用户的前两个信息信号和后两个信息信号的解调方式相同,故只分析前两个信息信号解调的误码性能。Z1,u和Z2,u可以表示为
A+B+C+D,
(18)
E+F+G+H。
(19)
式(18)展开如下:
(20)
(21)
(22)
(23)
同理,式(19)展开如下:
(24)
(25)
(26)
(27)
以式(18)为例,展开式中A为有用信号项,B为信号和信号之间的干扰项,C为信号与噪声的干扰项,D为不同噪声之间的干扰项。由式(3)可得,展开式中B项为0。同理,式(19)中F=0。
式(18)中A、C和D项之间相互独立,且由中心极限定理可得,各项都可以近似为高斯分布。故可得式(18)的均值和方差分别为
(28)
(29)
同理,式(19)的均值和方差分别为
(30)
(31)
(32)

将均值、方差和式(6)代入式(32),可得
(33)
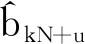
(34)
则IMU-HE-DCSK在多径瑞利衰落信道下的误码率公式为
(35)

(36)
对于L径独立且信道增益相同的多径瑞利衰落信道,γb的概率密度分布[20]为
(37)

(38)
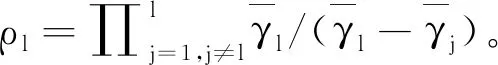
由于信道的参数是不断变化的,故利用数值积分法可得系统在多径瑞利衰落信道下的误码率公式为
(39)
从式(39)中可得,在多径瑞利衰落信道下,扩频因子β、用户数N以及信道参数αl都可以影响BER。令式(36)中α1=1,α2,…,αL=0,γb=Eb/N0,可以得IMU-HE-DCSK在加性高斯白噪声信道下的误码率公式为
(40)
由式(40)可得,当除用户数N以外的其他参数固定时,存在一个最佳的Nopt值,使得本系统的BER达到最低。设函数φ(N)为
(41)
式(41)两端对N求一阶导数且令导数为零,得最佳用户数Nopt为
(42)
由式(42)可得,当β固定时,系统最佳用户数随着信噪比的不同而变化。
2.2 传输速率、能量效率及安全性分析
通过比较IMU-HE-DCSK与HE-DCSK的传输速率和能量效率,可体现本文所提出系统的优越性。IMU-HE-DCSK与HE-DCSK系统的传输速率分别为RIMU-HE-DCSK=2N/βTc和RHE-DCSK=1/βTc,并代入式(43)信息速率增强百分比公式(DRI)。同样计算出两系统的平均比特能量Eb,HE-DCSK=3/2和Eb,IMU-HE-DCSK=(N+1)/N,并代入式(44)比特能量节约百分比(ESI)公式:
(43)
(44)
由式(43)、(44)可得,N值是DRI和ESI唯一的影响因素。随着N的增大,相较于HE-DCSK系统,IMU-HE-DCSK传输速率增强了2N-1倍,且节省的能量也逐渐趋于33.3%。
IMU-HE-DCSK系统的平方幅度谱如图5所示。由于IMU-HE-DCSK采用正交两路叠加传输的方式,并且每条支路上同时传输参考信号的叠加及多个用户信息,导致在图5的平方幅度谱中表现出类噪声性的特性,使得窃听者无法从平方幅度谱中分离出有用的信息信号,确保了信息传输的安全性。
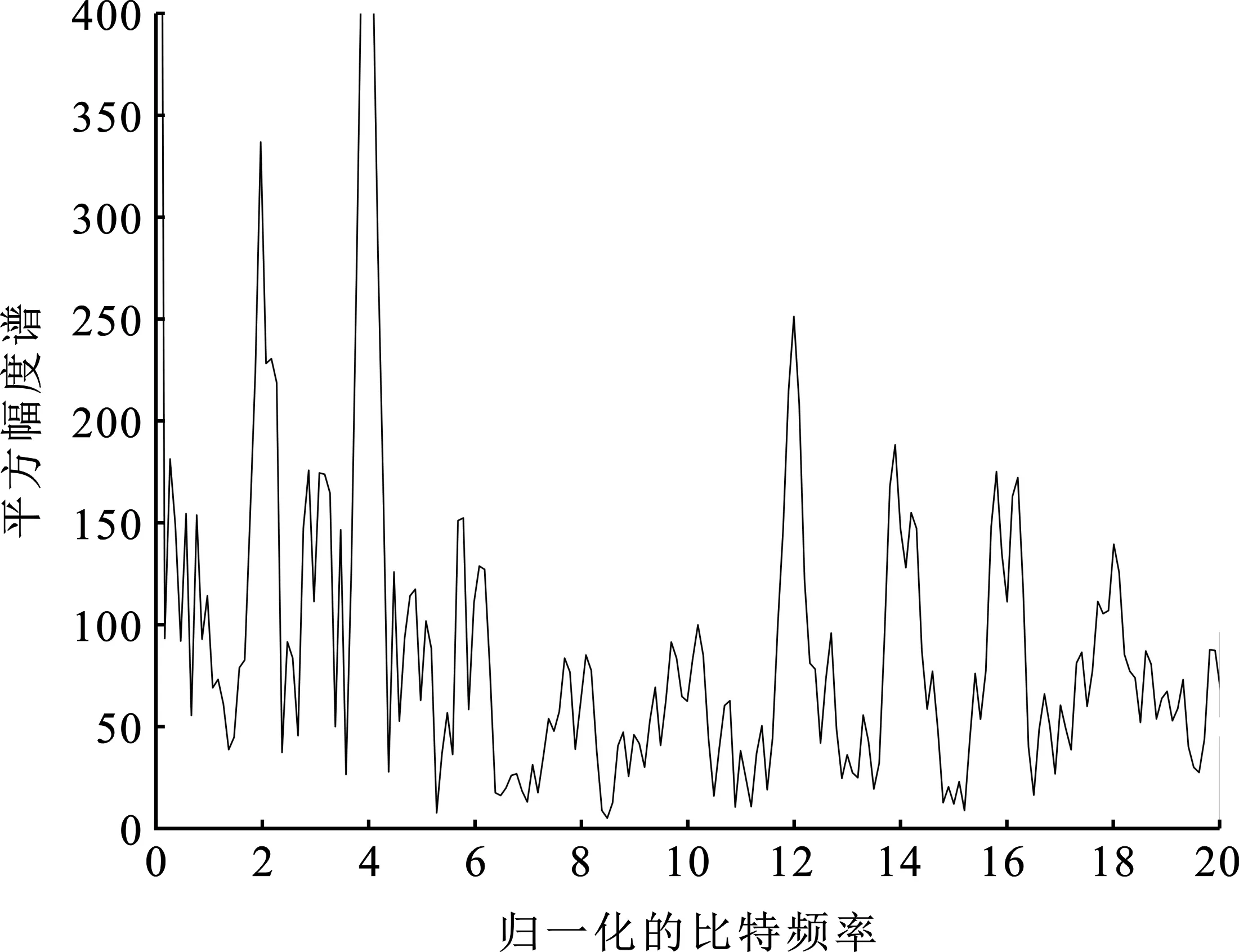
图5 IMU-HE-DCSK平方幅度谱
3 仿真结果
首先对正交混沌信号发生器进行了仿真并得到输出波形图,验证其输入信号的正交性;随后,对IMU-HE-DCSK的整体进行蒙特卡罗仿真,验证了系统的可行性与优越性。
3.1 OCG波形分析
图6是β=50时,第k帧的一段混沌序列通过正交混沌信号发生器产生两段混沌序列的波形图。

图6 OCG输出信号的波形图
图中,OCG产生的混沌序列xi,k、yi,k前半段波形重合,后半段波形相反。因此可得xi,k、yi,k两段混沌序列的相关值为0,验证了输入到IMU-HE-DCSK的两段混沌序列是正交的。
3.2 IMU-HE-DCSK仿真分析
在加性高斯白噪声信道和多径瑞利衰落信道条件下对IMU-HE-DCSK整体进行蒙特卡洛仿真,并与推导的理论值进行对比。
图7为N=2和Eb/N0取值分别为8 dB、10 dB、12 dB、14 dB时,加性高斯白噪声信道下的系统BER性能随β变化的仿真图,其中,The为理论值,Sim为仿真值。从图7中可以看出,随着β的减小,仿真值与理论值之间逐渐偏离,这是由于高斯近似法的局限性造成的,当扩频因子β较小时,在接收端相关器输出的判决变量中各项并不能近似为高斯分布,导致仿真值与理论值存在偏差。此外还可从图中得到,随着β的增大,不同信噪比下系统误码性能也逐渐恶化,且最终趋于一个定值。

图7 不同Eb/N0时,系统BER性能随β的变化曲线
图8为β=256、N取不同值时,在加性高斯白噪声信道下的系统BER性能随Eb/N0变化的仿真图。从图中观察到,在不同用户数N时,仿真值的点和理论值曲线十分吻合,验证了理论推导的正确性,也证实了利用OCG与正交调制能有效抑制各信号间干扰。还可以观察到,图中不同Eb/N0下的最小BER值不是同一个用户,说明不同Eb/N0存在对应的最佳用户数,可获得最佳误码性能。

图8 不同N时,系统BER性能随Eb/N0的变化曲线
为了更加直观地看到不同Eb/N0下最佳用户数的变化,绘制了图9曲线。图9为β=256且不同Eb/N0时,加性高斯白噪声信道下的系统BER随N变化的仿真图。图9中,随着N的逐渐变大,不同Eb/N0的系统BER值趋势总是先减小后增大,证明了理论推导的Nopt是存在的。每一个Eb/N0都存在一个最佳用户数Nopt,使系统的误码性能达到最佳。从图中可得,Eb/N0为8 dB、10 dB、12 dB、14 dB、16 dB时的最佳用户数分别为5、4、3、3、2。

图9 不同Eb/N0时, 系统BER性能随N的变化曲线
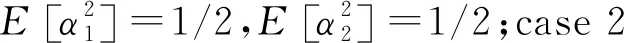
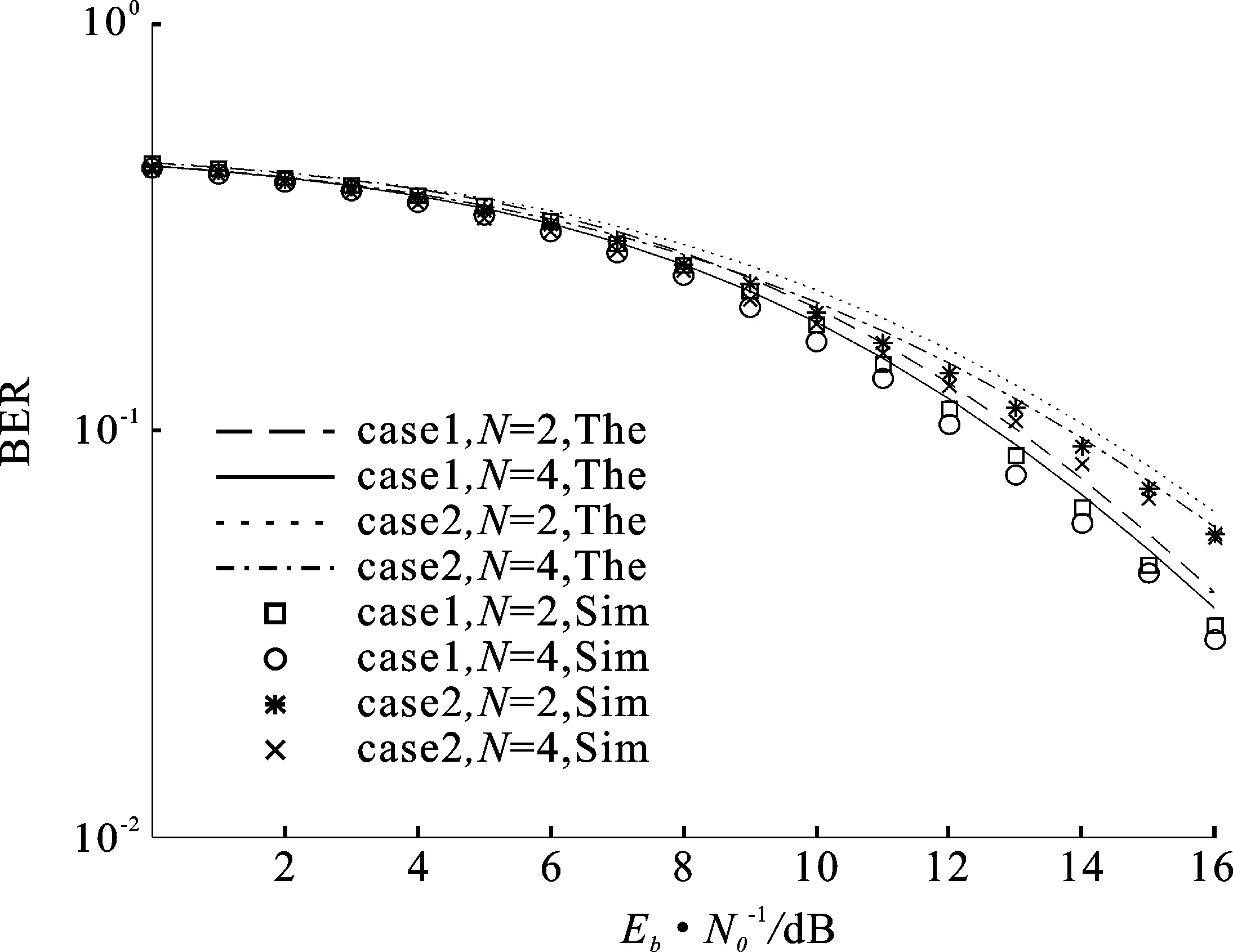
图10 不同情况下,系统BER性能的变化曲线
图11对比了β=256时,5个系统:IMU-HE-DCSK、NISI-MU-CDSK、SR-MUDCSK、OMU-DCSK和HE-DCSK在不同信道中的误码性能,图中设置各多用户系统发送相同数量的信息比特。从图11(a)中可以看出,当Eb/N0≤9 dB时,IMU-HE-DCSK和NISI-MU-CDSK误码率基本相同,且误码率低于其他系统的误码率;但当Eb/N0>9 dB时,NISI-MU-CDSK误码率最优,其次为IMU-HE-DCSK。在图(b)中可以看出,只有NISI-MU-CDSK误码性能相较IMU-HE-DCSK误码性能有所提升,其他系统性能均低于IMU-HE-DCSK。这也说明了NISI-MU-CDSK中的FDM技术可以减少多用户数据传输中的干扰。
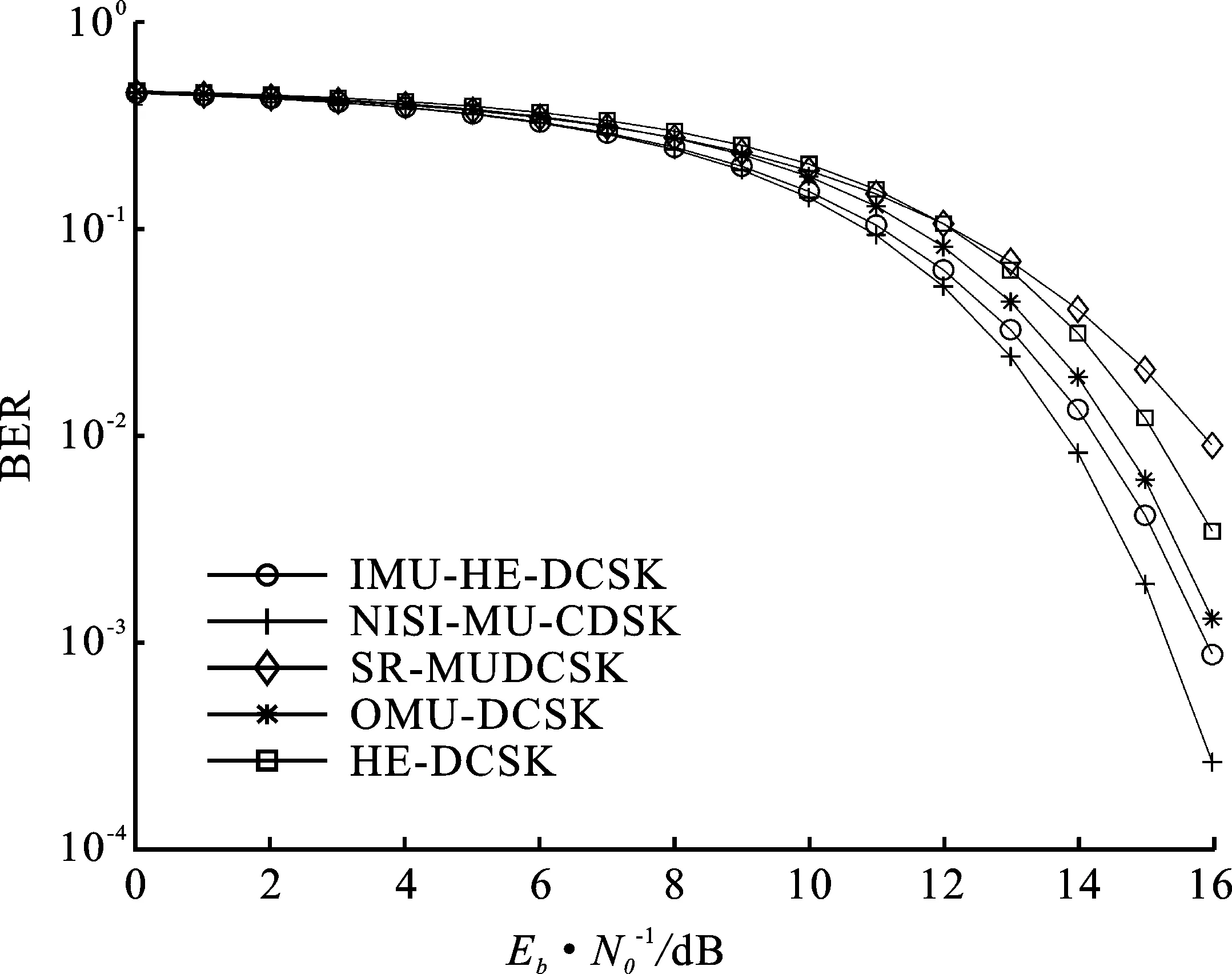
(a) 加性高斯白噪声信道
在表1中对比了5个系统的传输速率和能量效率。从表中可得,IMU-HE-DCSK的传输速率和能量效率均为最高。
图12为β=256、N=2时,在多径等增益瑞利衰落信道中BER性能的仿真图,其中多径路数L分别取2、3、4、5。从图12观察可得,路径数L的增加导致IMU-HE-DCSK的误码率降低,这也证明利用信道中多径分集的特性可以改善系统的性能。
4 结束语
在传统HE-DCSK系统的基础上提出了一种IMU-HE-DCSK通信方案。系统发送端利用Walsh码序列传输多个用户信息,并通过引入正交调制和正交混沌信号发生器,使系统的单用户传输速率比HE-DCSK系统提高了1倍,同时也有效抑制了不同信息比特之间的干扰。在接收端的均值滤波器对参考信号进行降噪,进一步减小相关器中噪声项的方差,从而降低系统误码率。最后通过高斯近似法推导了加性高斯白噪声信道和多径瑞利衰落信道条件下IMU-HE-DCSK的BER公式,并进行了实验仿真。结果表明,相较HE-DCSK,该系统传输速率提升了2N-1倍,节约的能量也逐渐随N的增大趋于33.3%,误码性能也提升将近1 dB。
