耦合粒子图像测速误差的连续伴随数据同化技术

邓志文，何创新，刘应征,*

1. 上海交通大学 机械与动力工程学院 动力机械与工程教育部重点实验室，上海 200240

2. 上海交通大学 燃气轮机研究院，上海 200240

近年来，随着实验流体力学与计算流体力学的迅猛发展，人们对湍流现象的认知和了解亦不断深入。常规认识湍流的途径主要是通过实验测量和数值模拟两种手段。然而，单纯依赖实验测量或数值模拟的手段已无法满足学界与工业界日益深入的研究需求。这和两者各自的局限问题是分不开的。实验测量方面，无论是传统的热线风速仪(Hot-wire Anemometer)，还是先进的粒子图像测速(Particle Image Velocimetry，PIV)技术，依然受限于实验测量成本高昂，测量区域有限，时空分辨率较低，实验数据类型单一，多物理同步测量难度大以及实验测量误差难避免。数值模拟方面，高精度的直接数值模拟(Direct Numerical Simulation, DNS)和大涡模拟(Large-Eddy Simulation, LES)需要消耗大量的计算资源，而计算效率高的雷诺时均(Reynolds-Averaged Navier-Stokes, RANS)模型大多基于半经验半理论公式，受限于模型结构形成缺陷和经验常数难精确给出，对复杂流场的模拟精度不高；此外，数值模拟的初始条件或边界条件在实际工程计算中常常难以准确获得。

为了弥补实验测量与数值模拟各自的不足，实现对高精度湍流流场的精准描述，数据同化(Data Assimilation, DA)作为一种深度融合实验数据和数值模拟的技术，近年来愈发受到国内外流体力学领域研究学者的关注。数据同化，最早应用于气象领域，随后拓展到水文、海洋及地质领域。数据同化的三要素有实验观测、系统模型和数据同化算法，其核心思想在于利用实验数据对系统模型进行结构上或参数上的调整修正，进而优化系统模型，提升预测性能。

数据同化算法主要可以分为两类：① 基于数据统计算法的数据同化，如卡尔曼滤波、集合卡尔曼滤波(Ensemble Kalman Filter, EnKF)等；②基于变分算法的数据同化，如3DVar (Three Dimensional Variation)、4DVar等。Kato等通过采用EnKF及其变种的同化算法，优化了翼型绕流的来流攻角、马赫数以及湍流涡黏分布，成功预测了翼型表面压力系数分布。本文作者团队用EnKF同化算法优化了不同RANS模型的模型经验参数，成功预测了自由射流速度场。然而，大部分滤波算法主要针对湍流模型的边界条件、初始条件、模型经验参数进行修正，因而同化效果有限。相对而言，变分算法则通过添加源项的方式优化模型结构，设置与实验观测相关的目标损失函数，推导伴随变分方程，通过求解目标损失函数极小值，便可修正优化湍流模型预测路径。He等在Spalart-Allmaras(SA)模型中添加了模型修正因子,通过连续伴随算法同化得到的分布，进而提升了SA模型对流动分离的预测能力。Foures和Symon等使用连续伴随方法直接对雷诺应力项进行同化，准确还原了翼型绕流的平均流场。He等继而提出了基于连续伴随的顺序数据同化算法，结合了顺序数据同化与变分数据同化的优势：既保留了变分算法的精度，又采用顺序同化的方式实时动态耦合实验观测值修正模型预测结果；这种方式避免了变分算法在时间上正向逆向的积分，算法计算效率更高。值得提出的是，连续伴随算法在实验观测准确可靠时，具有很好的同化效果，而实验测量误差这一重要因素如何在同化算法中准确考虑，无疑是很重要的。

本文在He等的研究基础上，从PIV互相关原理的不确定度出发，提出了耦合PIV实验误差的连续伴随同化算法，优化了原变分算法的目标损失函数以增强该同化算法的鲁棒性。为了验证算法的可行性，本文先对已知PIV流场植入合成误差，进行同化对比测试，继而对PIV互相关算法的不同参数设置所获得的流场进行同化研究。结果表明，相比原变分算法，耦合PIV实验误差的变分算法能够对实验观测数据去伪存真，抗误差干扰能力明显提升，鲁棒性更强，实现对湍流流场的准确预测。

1 算法模型原理

1.1 算法框架设计

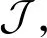
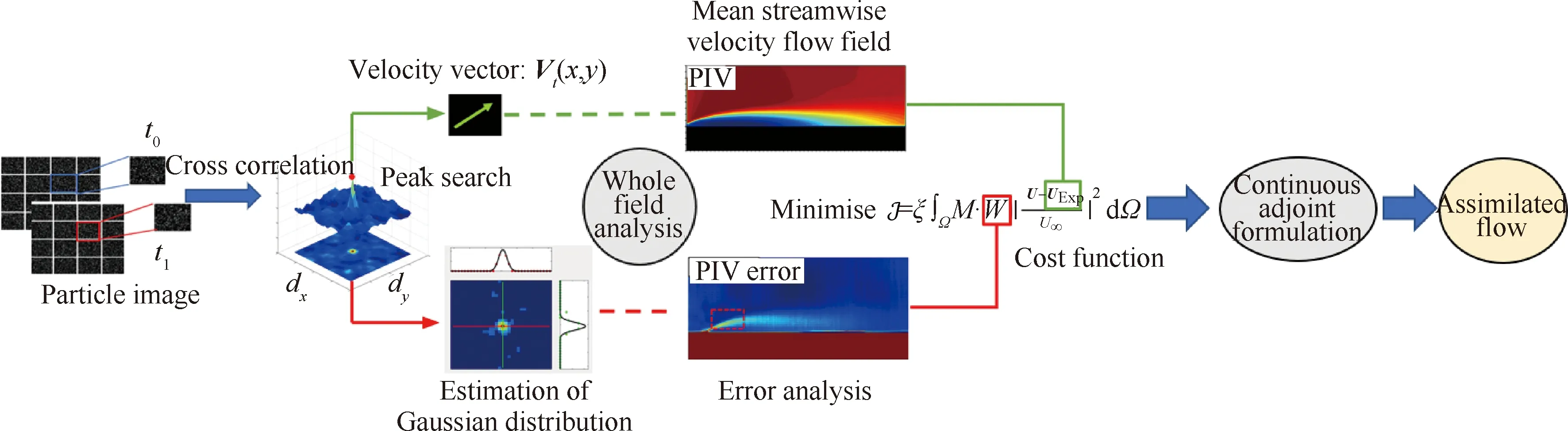
图1 耦合PIV实验误差的连续伴随算法流程Fig.1 Flow chart of continuous-adjoint algorithm coupled with PIV error

1.2 PIV实验误差分析

为了定量表征PIV实验误差的分布，本文提出了全场各点实验权重分布函数。本节将从粒子图像测速的互相关算法原理出发，详细阐述实验权重分布函数的提取实现过程。

粒子图像测速技术是通过在流场中布撒示踪粒子跟随流体运动，利用激光加强粒子反射，经由相机在极短的时间内双次或多次曝光，拍摄记录粒子的运动轨迹，分析相邻两帧的粒子图像从而获得流场的速度信息。其中，流动速度矢量的获取通常采用图像互相关算法。该算法是假设在相邻两帧图像中，被测流体的速度保持不变，并且粒子之间的相对位置在空间上保持一致，然后将粒子图像划分成若干个子区域(即问询区域)，通过逐个区域粒子群的互相关计算，获得其与临近区域的相关性。传统相关性的计算表达式为

=∬(,)·(+Δ,+Δ)dd

(1)

式中：(,)和(,)分别对应两帧图像某一问询区域的灰度分布函数；Δ、Δ分别为粒子在、方向的移动距离。如图2(a)所示，当Δ、Δ等于粒子在、方向的真实位移时，互相关计算平面就会出现一个峰值，表明此处的相关性最大，可作为该区域粒子的平均运动位移，将其除以运动时间即可获得速度矢量，即该子区域内粒子群的平均速度。为了节省计算资源，提高运算效率，一般采用基于傅里叶变换的互相关函数计算，如式(2)～式(4)所示:

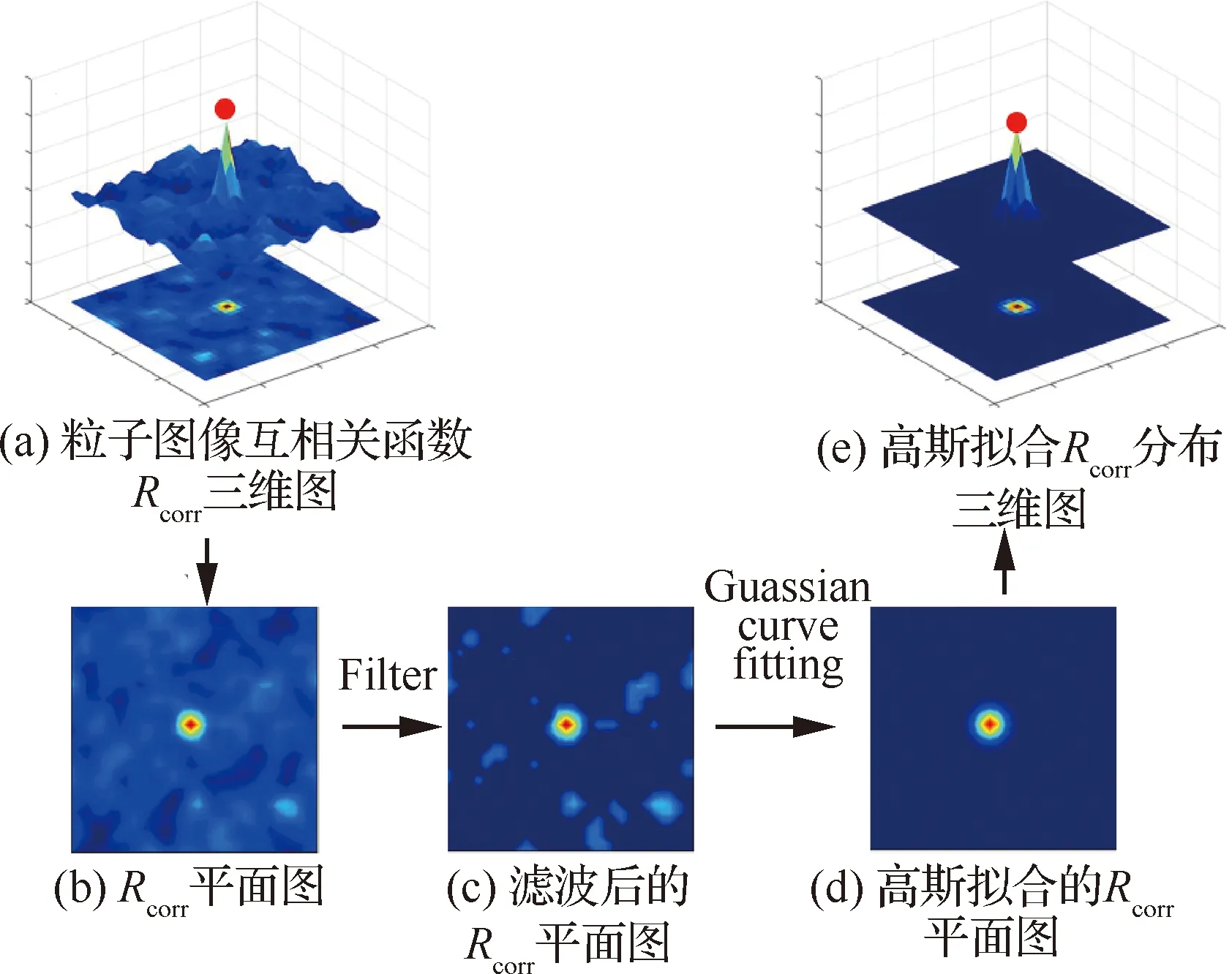
图2 PIV实验误差分析Fig.2 Procedure of PIV error analysis

(,)=((,))

(2)

(,)=((,))

(3)

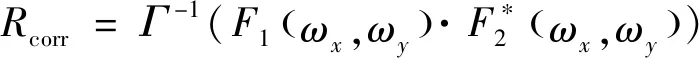
(4)

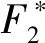
如上所述，通过式(2)～式(4)计算便可获得互相关函数的分布，如图2(b)所示。经由图像分析可知，该相关性分布总体呈现出二维高斯分布特征。因而，本文采用二维高斯分布函数对各个问询区域的互相关函数进行独立的拟合表达(～(,Δ,Δ,,))。设其概率密度函数(,)为

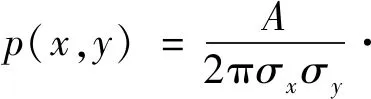
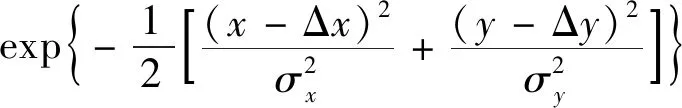
(5)

式中:为高斯分布的峰值大小;、为、方向所对应的位移方差。和的数值大小与PIV实验的误差密切相关，、数值越大表明此处的实验值不确定度越高，误差越大，实验数值越不可信。

为了更好地拟合高斯分布规律，排除虚假相关干扰的影响，本文设置截断滤波，滤波阀值为0.1倍的峰值，即相关性小于滤波阀值的点将置于0，如图2(c)所示。在经过滤波处理过后，采用最小二乘法对高斯分布中的未知参数进行拟合，拟合结果如图2(d)所示。最终分析对比高斯分布重构的互相关函数分布(图2(e))与原始粒子图像测算的互相关分布(图2(a))情况，可以发现排除虚假相关干扰后，二者分布规律基本一致，采用此算法可以很好地重构的分布规律。

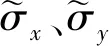
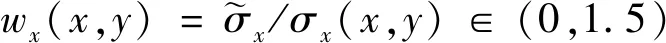
(6)

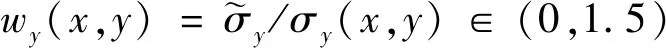
(7)

1.3 连续伴随同化算法原理

本文的研究目标主要是针对平均场的数据同化，因此采用的实验观测为PIV平均场数据，同化的模拟结果为稳态结果。本文所采用的连续伴随同化算法是由何创新等在Foures等的基础上进行改进的，如式(8)所示，算法的核心思想是在稳态Navier-Stokes方程中加入同化控制源项，通过优化源项的分布，进而不断减小实验观测与模型预测之间的误差。

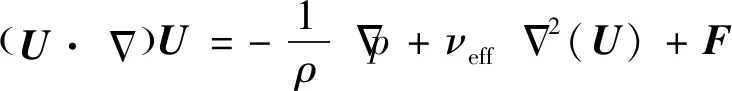
(8)

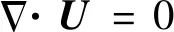
(9)

式中：、、分别为速度矢量、压力和流体密度；为等效黏度，即流体分子黏度与湍流各项同性涡黏部分之和，可以通过RANS模型直接计算获得;为各项异性涡黏，可通过伴随变分求解。原连续伴随的目标损失函数为

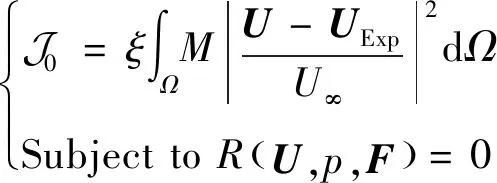
(10)

式中：为实验观测速度；为无穷远处的来流速度；代表数值模拟的计算区域；为单位无量纲转换系数；为Navier-Stoke方程和连续性方程约束；作为掩模函数指定了实验观测所在的位置：当=1时，表明此处有实验观测约束，反之为0，则表明无实验观测。

为了求解目标损失函数的极小值，引入拉格朗日函数进行变分方程的推导求解：

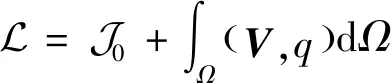
(11)

式中：、为伴随速度变量和伴随压力变量，经过变分推导可得伴随变分方程组为

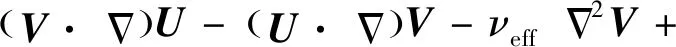
(12)

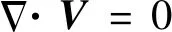
(13)

连续伴随的数据同化过程，可以看作是求解目标损失函数的极小值过程。通过不断优化迭代的分布，最终使得速度场既满足实验观测规律又满足Navier-Stokes方程以及变分方程的约束。平均场的同化计算迭代流程图如图3所示。图中、为初始流场的速度和压力；、分别为计算相对误差和人为设定的收敛误差值；为松弛因子，控制的迭代速度。本文通过引入实验观测权重分布函数修正模型的目标损失函数，如式(14)所示，从而将PIV各个速度矢量的实验误差与连续伴随同化算法迭代计算相耦合，进而提升该算法的抗误差干扰能力。

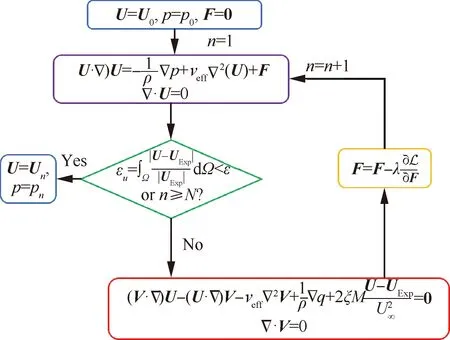
图3 平均场的连续伴随数据同化计算迭代流程Fig.3 Iteration procedure of continuous-adjoint based DA for mean flow field

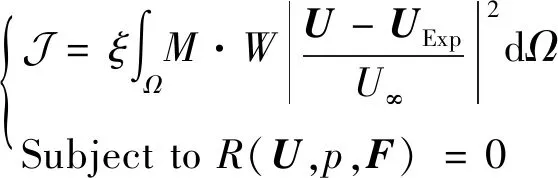
(14)

2 实验设计验证

为了验证所提同化算法的有效性和鲁棒性，本文采用有限长平板绕流的PIV实验数据作为同化过程中的实验观测输入。对于此类分离再附流动，大多RANS模型难以精准预测，与实验结果相差甚远，因而需要数据同化技术进行优化。该实验的原始数据来源于文献[28]。

该实验是在一个300 mm (高)×300 mm (宽)×2 000 mm (长)的低速开式风洞中进行的。为了消除风洞壁面对流动二维性的影响，平板厚度设计为=24 mm，弦厚比为=9，并垂直安装于风洞测试段的正中间位置。本实验中自由来流的流速保持在=10 m/s，依据平板厚度计算对应的雷诺数为=15 800。如图4所示，为了捕捉平板绕流的分离与再附现象，实验数据的观测区域(Region of Observation，ROB)选定于平板正上方的流场(0≤≤9,0≤≤25)。本实验采用Di-Ethyl-Hexyl-Sebacate (DEHS)油滴作为示踪粒子，粒径为1 μm左右，对实验流体具有良好的跟随性。激光平面由Nd:YAG激光器(135 mJ/pulse, 532 nm, 8 ns, Litron, UK)产生，厚度为1 mm。采用CCD相机(IPX 16M, IMPERX, USA)对粒子的运动图像进行采集记录。激光脉冲频率与相机采样速率由同步器控制，均保持在1 Hz。最终共采集6 000幅图像，图像分辨率为4 872 pixel×3 248 pixel。通过PIV互相关算法可计算获得3 000 个速度矢量场，求平均可得PIV实验的统计平均流场。关于此实验更详细的描述和进一步的结果可在文献[28]中获得。

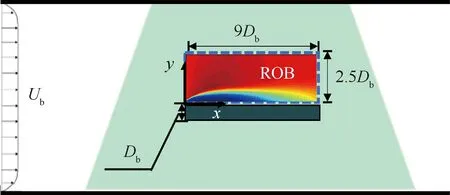
图4 实验装置示意图Fig.4 Schematic diagram of experimental setup

3 结果分析讨论

为了全面充分地验证本文算法的优化效果，本文对比了原连续伴随算法以及改进后的算法在不同误差环境下的同化效果。首先对不同程度的合成误差干扰进行了测试验证，随后进一步对不同PIV互相关算法设置引入的算法误差进行同化效果测试。

图5为PIV实验粒子图所获得的全场速度矢量的误差分布云图，颜色越蓝代表此处的互相关性越高，不确定度越低，即实验误差越小，实验观测结果可信度高。如图5(a)所示，平板上方的主流流动区域颜色较蓝，表明实验误差小，较为可信，因而实验权重分布值较大。偏离蓝色的区域主要集中于平板绕流的剪切层附近以及近壁面区域，这是因为剪切层附近的流动比较紊乱，而近壁区域存在壁面反射，因而实验结果误差较大。图5(b) 是剪切层附近的局部细节放大图，每一块子区域都表示一个速度矢量的互相关函数分布情况，能够通过1.2节所述方法进行高斯分布拟合。图5(c)为经过误差分析后转换得到的实验权重分布函数。对于实验误差相对较高的壁面和剪切层区域权重分配较小，而误差较小的自由来流区域的权重分配较大。

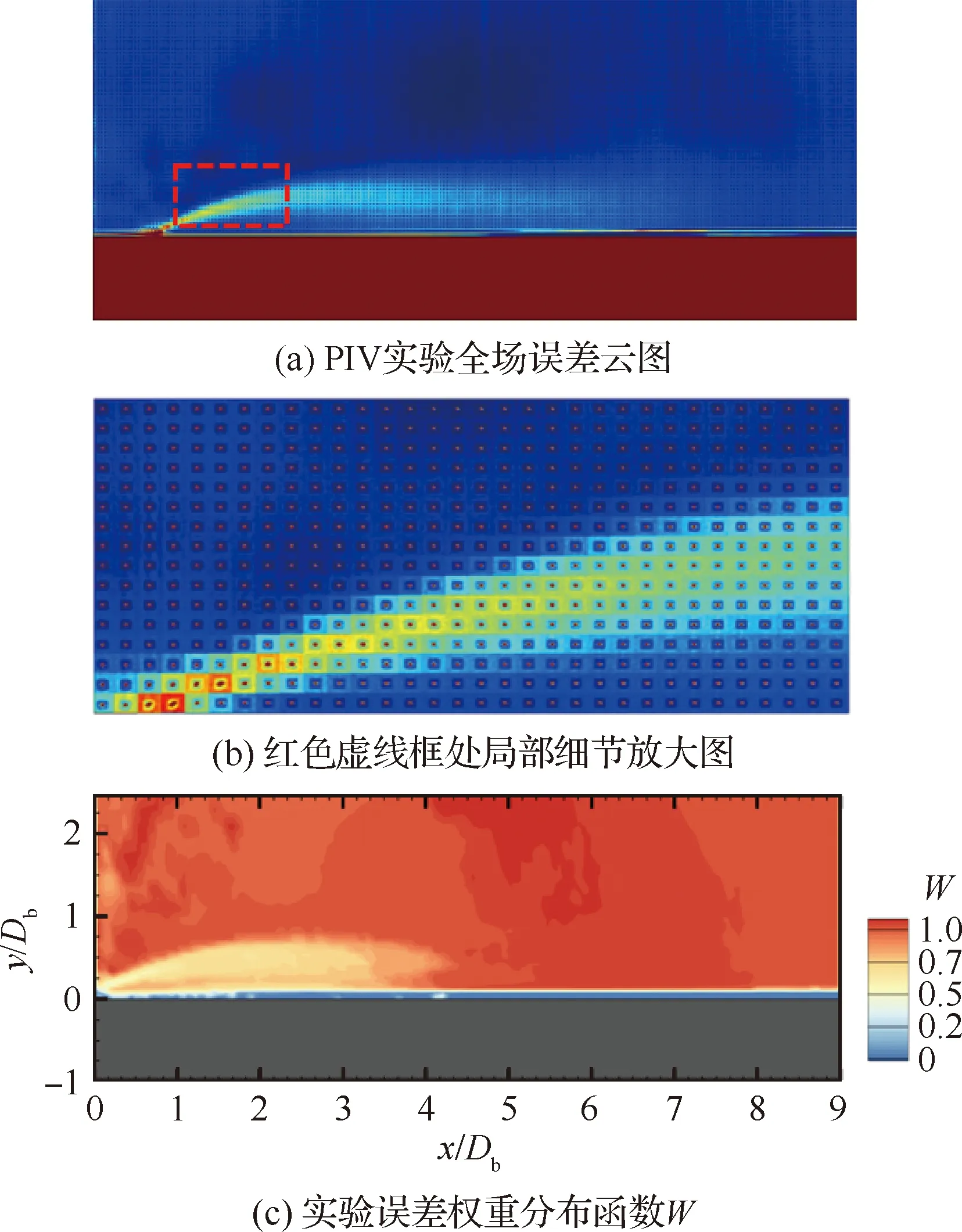
图5 钝体平板绕流PIV实验误差分析Fig.5 Analysis of PIV error of flow around blunt plate

3.1 合成误差对同化效果的影响

图6为添加不同级别的合成误差干扰后所得的流向速度平均场()云图对比。图6(a)为采用最优的PIV算法参数设置所得的统计平均场结果，亦作为本次同化实验中的真实速度。合成误差的干扰程度主要由参数控制，如式(15)所示。

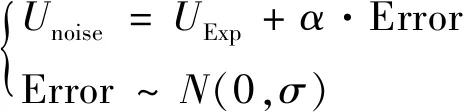
(15)

图6(b)～图6(c)中为添加不同程度的实验干扰后的平均速度云图，对应=01,02,05的情况。合成误差的添加规律与PIV实验误差分布相关，即在壁面及流动剪切区域的合成误差较高，同时由图6(d)可知当=05时，合成误差已对实验结果产生了较大的影响，因而本研究中的最大值为0.5。将带有合成误差的PIV结果(图6(b)～图6(d))作为实验观测输入进行同化对比测试，最终同化效果如图7～图9所示。通过对比研究发现，当采用带有合成误差的实验结果进行同化时，原连续伴随同化模型(如图7(a)～图7(c) Adjoint结果，图8中蓝色实线)为了尽可能地同化带有误差的实验值(对应图8 中PIV+结果)，出现了极不合理的预测结果，违背了真实的流动分布规律(对应图8 中Ref结果)。尤其在近壁面的速度容易被该区域内误差较大的速度分布所干扰(图8中绿色圆点)，进而导致整体同化效果很差，流动计算发散。而当采用耦合PIV实验误差的同化模型时(如图7(a)～图7(c) Adjoint+结果，图8红色实线)，则可降低合成误差的干扰，提升计算收敛的稳定性，同时相比传统的SA模型预测结果有很大的改善，对流动剪切的预测更为精准，与真实的流动速度分布曲线吻合良好。

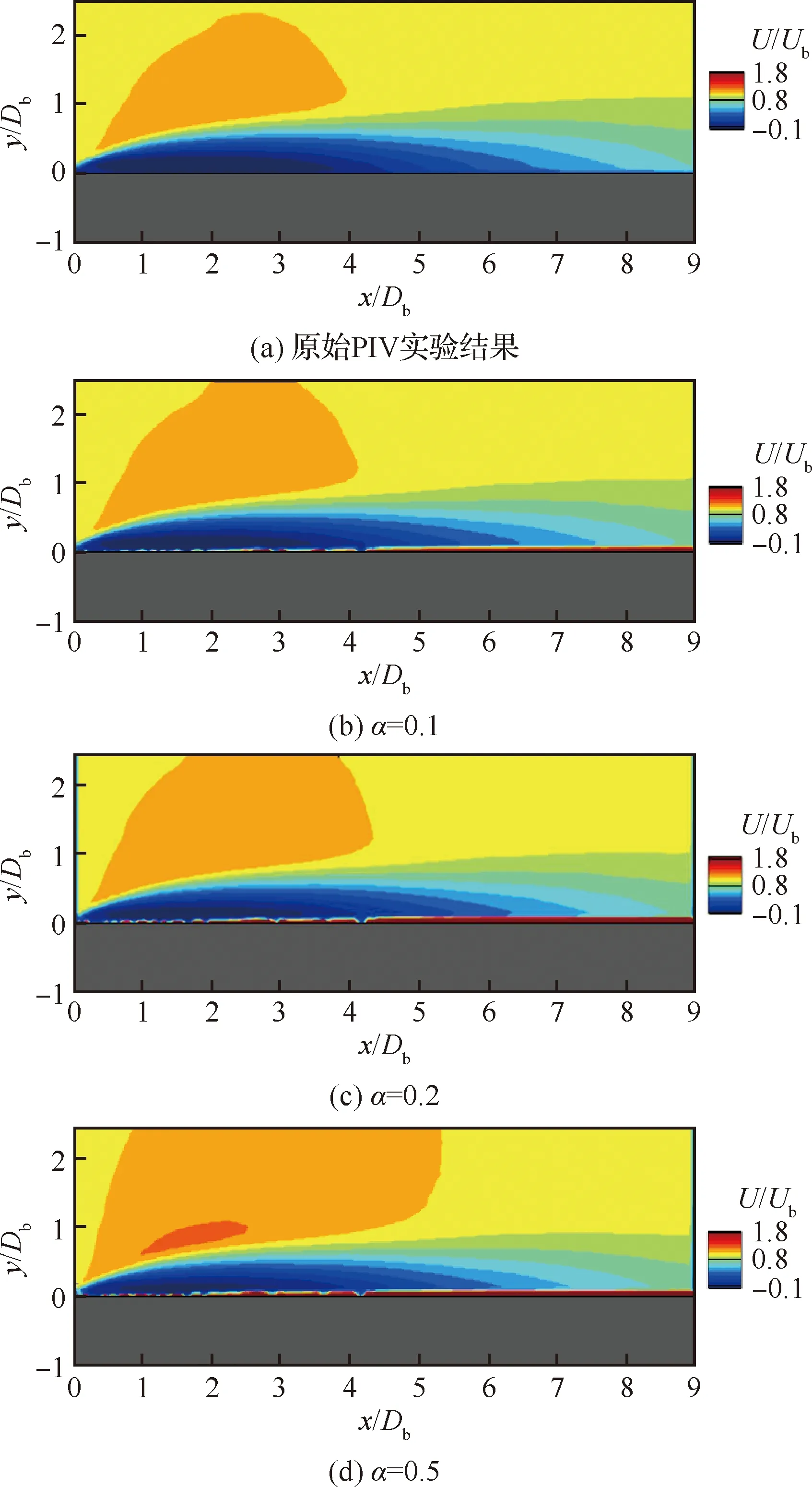
图6 添加不同合成误差所对应的流向速度云图Fig.6 Contours of streamwise velocity adding different levels of synthetic error

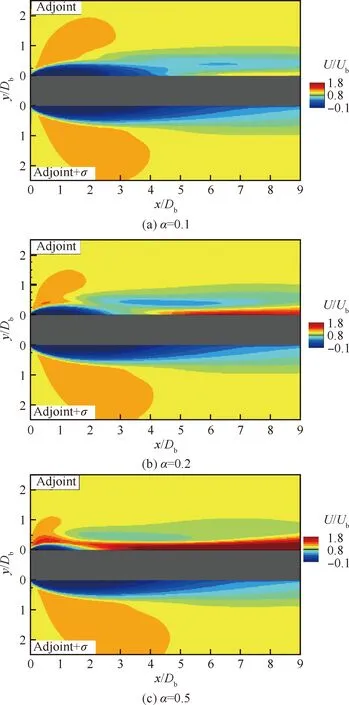
图7 不同合成误差下采用不同同化方法的结果对比云图Fig.7 Contour plots of assimilated results with different synthetic errors using different data assimilation methods

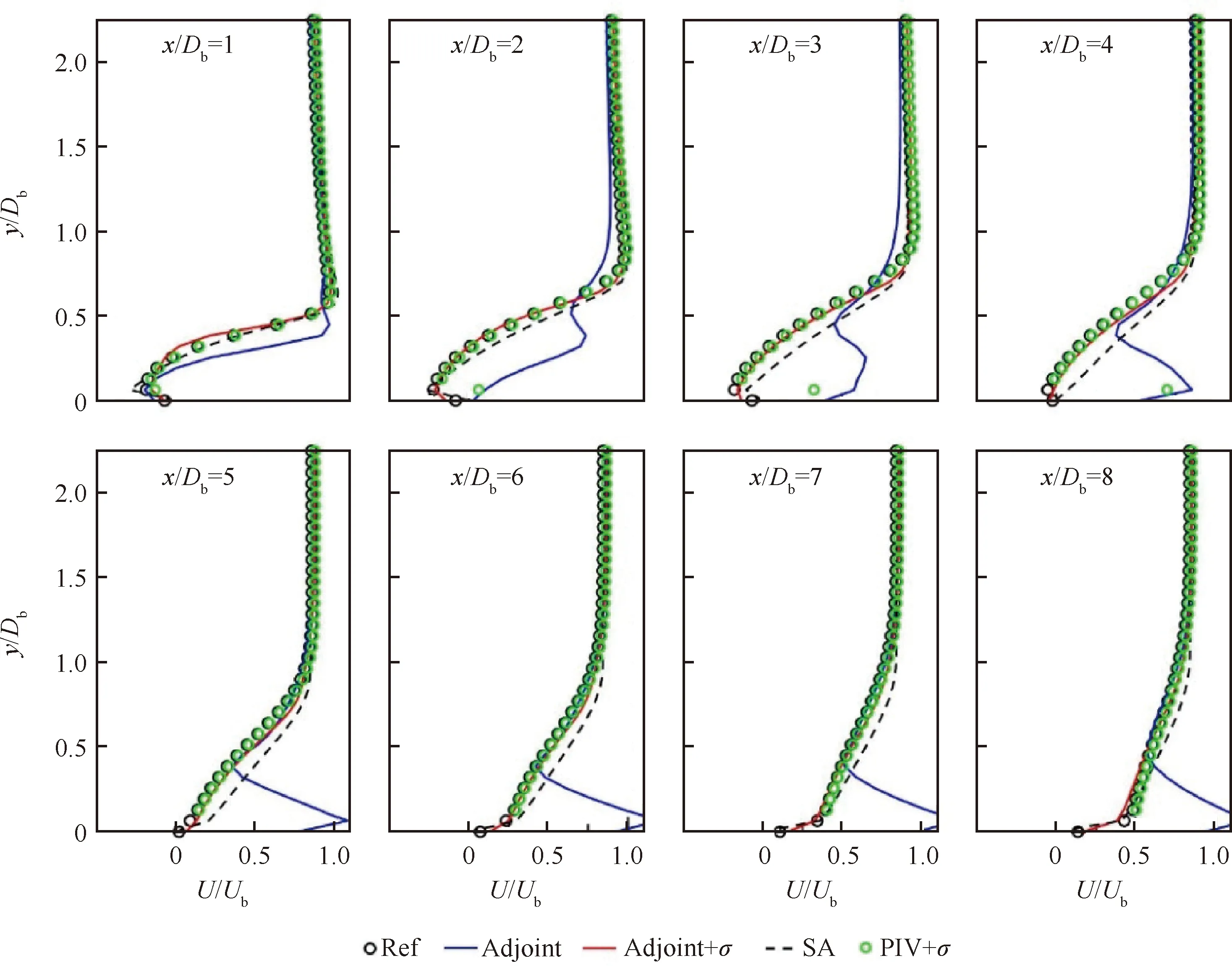
图8 不同位置处流向速度对比曲线(α=0.2)Fig.8 Transverse profiles of streamwise velocity at different locations (α=0.2)

图9为平板流动再附点位置以及流线图对比结果。从图中可以看出，耦合PIV实验误差的数据同化模型(图9(b)～图9(d))与PIV结果吻合良好，对分离再附点的位置预测结果准确，且即使在高合成误差场景下(图9(d)，=05)，依然有很高的预测精度。

图9 不同合成误差下流场流线图以及再附点位置分布Fig.9 Streamlines and location distribution of reattachment point obtained using data assimilation method with different synthetic errors

3.2 PIV算法参数设置对同化效果的影响

为了进一步验证所提同化算法的有效性和鲁棒性，本文采用不同的PIV算法设置所获得的流场作为同化的观测输入进行研究。采用不同的PIV互相关算法参数设置对同一流场的粒子图进行分析所得的计算结果也有所不同。如当问询窗口的尺寸发生变化时，PIV计算的速度矢量数量及其对应的误差大小也随之发生改变。为了便于理解和讨论，本文中将这部分仅由不同PIV算法参数设置所引起的误差，简称为“PIV算法误差”。

如图10所示，当不对原粒子图进行任何预处理(诸如图像对比度增强以及噪声滤波算法等)，并采用不同的问询窗口设置时(24×24,32×32,48×48)，PIV算法的计算结果会产生较大的计算误差，尤其在近壁面区域。图10白色圆圈内的流动与真实的流动现象并不相符，分离泡对壁面的依附出现失真，无法准确捕捉再附点位置。

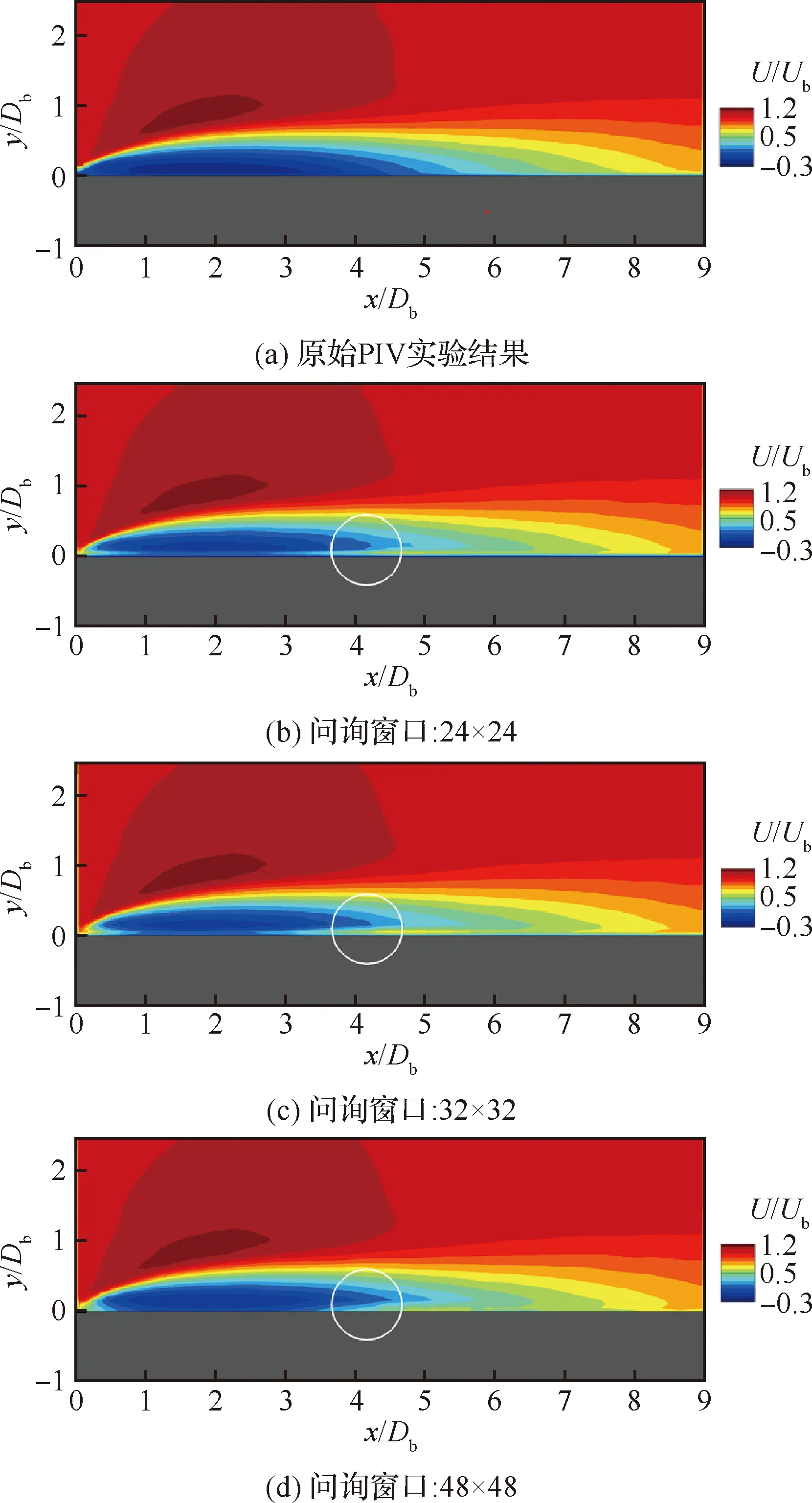
图10 采用不同问询窗口计算所得的流向速度云图Fig.10 Contours of streamwise velocity calculated using different sizes of interrogation windows

图11为当采用不同问询窗口时，实验权重的分布函数云图。如图所示，针对本文的验证案例，当采用较大尺寸的问询窗口(48×48)，PIV实验结果的误差会有所减小，相应地，其所对应的实验权重分布函数的权重值会有所增大(图11(c))。而当问询窗口尺寸较小时(24×24)，所对应的实验权重值较小。观察实验权重的分布可得，近壁面及剪切流动区域的实验误差较大，实验权重取值小。当问询窗口较小时(图11(a)和图11(b))，近壁及剪切区域的权值分布接近于0，证明此处的实验结果误差很大，实验观测不可信。

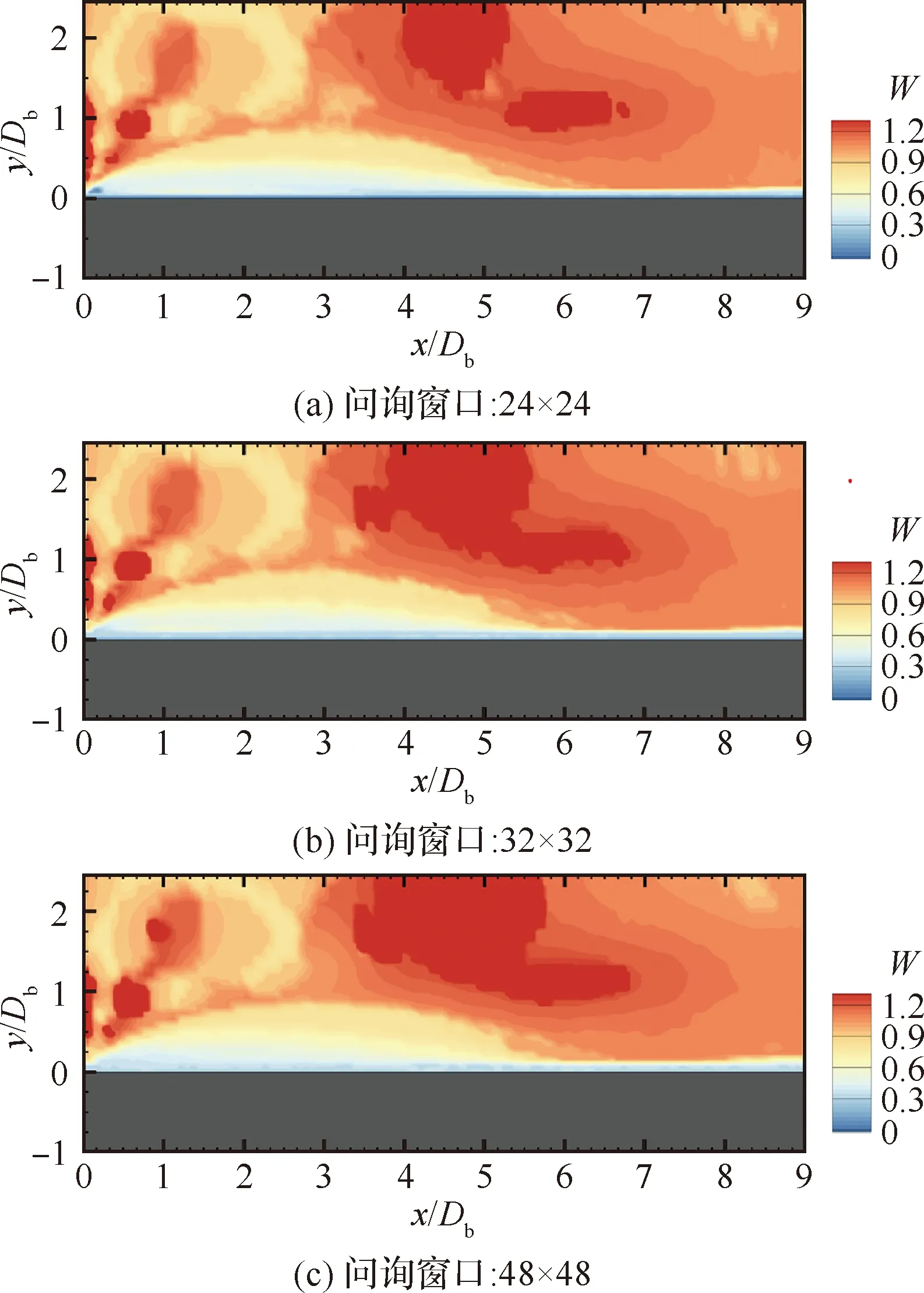
图11 采用不同问询窗口所得的实验权重分布函数云图Fig.11 Contours of experimental weighting function distribution obtained using different sizes of interrogation windows

将不同PIV算法所得的实验结果(图10(b)～图10(d))作为实验观测进行同化测试，最终同化结果如图12～图14所示。图12为流向速度的平均场云图，由图可得，相比于实验结果(图10 (b)～图10 (d)，图13绿色圆点)，两种数据同化算法计算收敛较好，未观察到分离泡依附失真现象。然而，仔细对比无误差引入的连续伴随模型(图12(a)～图12(c)中Adjoint结果，图13 蓝色实线)与耦合PIV误差的同化模型(图12(a)～图12(c) 中Adjoint+结果，图13红色实线)，可以发现，原伴随变分模型的预测结果在剪切层附近存在速度变化不光滑不连续现象，且对近壁面的流动结果预测并不准确。而耦合实验误差修正的同化模型所得的流场速度曲线连续光滑，不存在较大的偏离值，与真实速度曲线分布(黑色圆点)具有良好的一致性。图14为平板流动再附点位置以及流线图对比结果，从图中可以看出，由于采用不同的PIV互相关算法参数设置，引入了除实验误差影响外的算法误差，导致流场的再附点位置存在较大的偏差(图14(a)～图14(c)中PIV计算结果)，与真值4.43(图9(a))相去甚远。采用原伴随变分同化算法所得再附点的位置(图14(a)～图14 (c)中Adjoint结果)会贴合含有实验误差和PIV算法误差的观测数据(图14(a)～图14(c)PIV计算结果)，并无明显的改善优化。而采用耦合PIV误差的同化模型时(图14(a)～图14(c)中Adjoint+结果)，同化结果受PIV算法误差干扰较小，其对再附点的位置预测更为准确，并且对流动模式预测良好，同化效果更好。

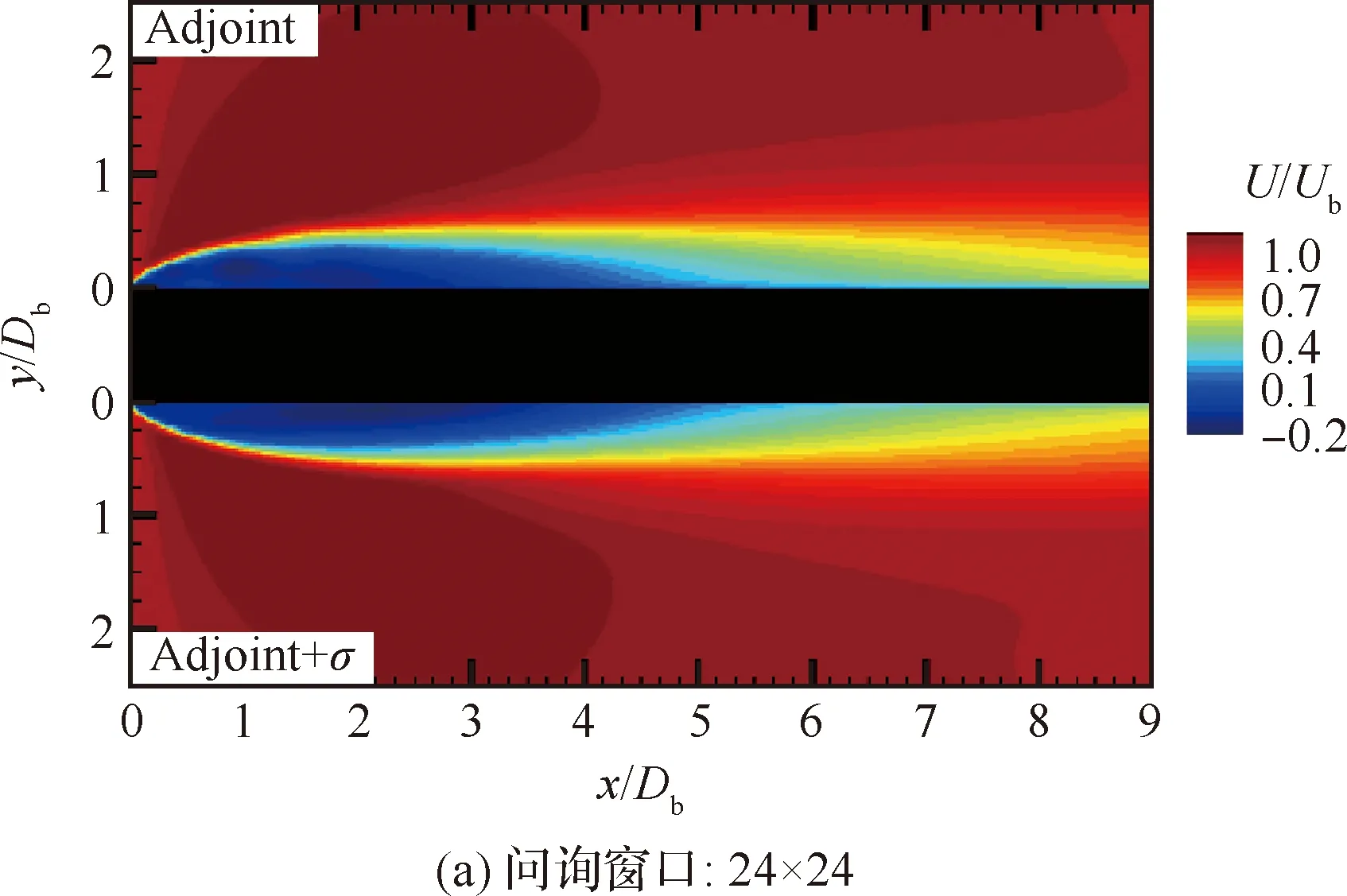
图12 采用不同同化模型在不同PIV算法误差下的同化结果云图Fig.12 Contours of assimilated results with different errors induced by different PIV algorithms using different data assimilation methods

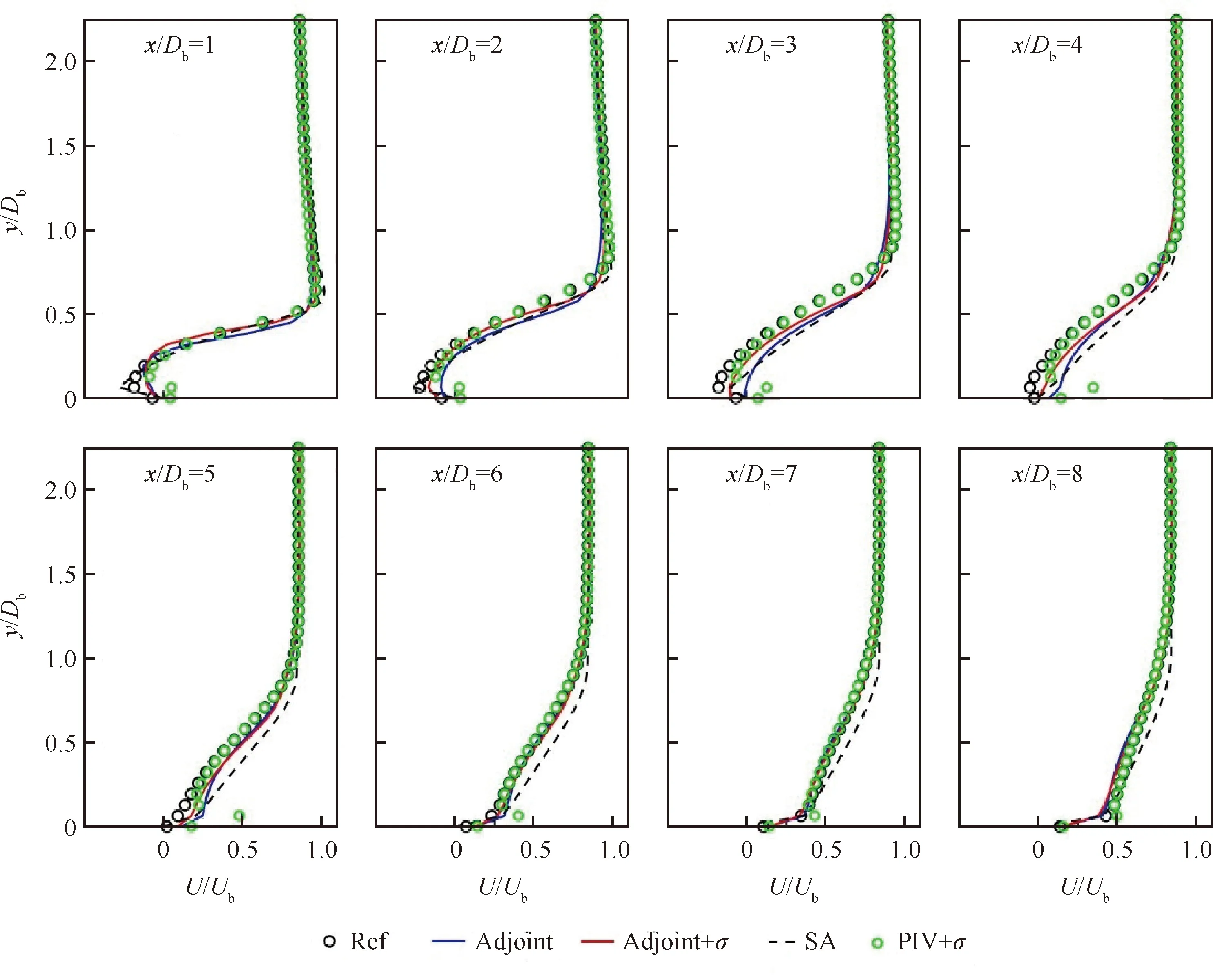
图13 不同位置处流向速度对比曲线 (问询窗口：32×32)Fig.13 Transverse profiles of streamwise velocity at different locations (interrogation window: 32×32)

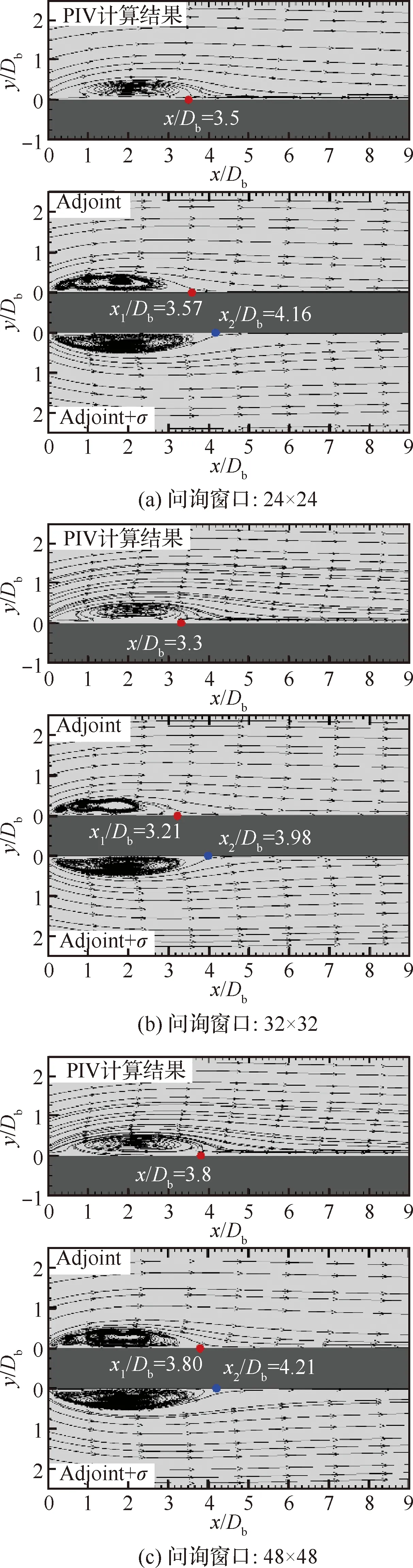
图14 不同问询窗口设置下PIV和同化结果的流场流线图及再附点位置分布Fig.14 Streamlines and location distribution of reattachment points determined by PIV and assimilated results obtained using different settings of interrogation windows

4 结 论

本文从粒子图像互相关的基本原理出发，推导获得反映PIV实验误差分布规律的实验权重分布函数，通过将其与连续伴随算法耦合，优化同化算法的目标损失函数以提升算法的抗误差干扰能力。为了验证所提算法的有效性和鲁棒性，本文先对已知PIV流场植入合成误差进行同化对比测试，继而对PIV互相关算法的不同参数设置所获得的流场进行对比研究，可以得到以下结论：

1) 从粒子图像互相关算法推导得到的PIV实验权重分布函数能定量反映PIV实验误差分布规律，能与连续伴随同化算法紧密耦合。

2) 在合成误差同化测试中，原伴随变分模型易受合成误差干扰，无法进行有效地同化，预测结果有悖物理规律。而耦合PIV实验误差的同化模型能够显著地降低合成误差的干扰，提升求解收敛的稳定性，准确预测流场的真实信息。

3) 在由PIV互相关算法的不同参数设置所获得的流场同化测试中，原伴随变分模型无法精准预测流场的细节，而耦合PIV实验误差的同化模型可以降低PIV算法误差的影响，对流场的预测结果较为准确，贴近流场真实分布规律，细节还原度高。

在后续的研究工作中，本文将进一步对所提算法的鲁棒性和普适性进行探究，如针对不同问询窗口、粒子浓度和粒子直径等多参数耦合作用下的PIV流场进行同化对比测试。同时开展对瞬态流场的同化对比研究，分析速度脉动、雷诺应力等统计量的同化精度。