适用于工程数据的飞行器气动特性修正框架
2022-07-04李金晟庄凌宋加洪卢宝刚苏伟吴乔
李金晟,庄凌,宋加洪,卢宝刚,苏伟,吴乔
北京航天长征飞行器研究所,北京 100076
气动特性预示是飞行器设计、发展及鉴定的重要组成部分,预示的精准度直接影响飞行器的控制效果和仿真可信度。飞行器气动特性预示的主要内容是建立气动模型并量化模型不确定度,预示的技术水平取决于理论计算、风洞试验和气动辨识3种技术途径的综合运用。但由于多数飞行器飞行试验缺乏有效激励且传感器测量精度较低,致使试验数据难以满足气动辨识的需求,故当前工程上主要采用前两种手段计算气动特性。获取的气动特性通常由地面气动数据表及先验不确定性模型进行表征,前者用来预测任意飞行状态下的气动系数,后者用于评估预测系数的可信区间。这种预示方式存在的主要问题是:地面气动数据表存在众多误差源,致使不确定性模型过于保守、给出的气动误差带安全余量较大。
近年来随着飞行试验数据的积累,如何利用多条试验数据进行气动特性修正,提高气动特性预示精准度,满足新型飞行器精细化设计需求,成为当前工程应用领域一大难题。基于地面气动数据表与不确定模型之间的相互依赖关系,可将该问题分解为两个子问题:如何修正地面气动数据表及如何量化修正后气动模型的不确定度。
针对第1个子问题,研究人员已做了大量的工作。文献[3]从模型验证角度提出了一种通用思路,即基于试验数据与预测数据之间的残差确定一个修正项,利用其来补偿原模型。修正项的表征可采用统计概率或模型拟合两种方法,后者构建的补偿差量模型具有更广的适用范围,故在气动特性修正领域得到了广泛应用。差量模型的确定本质是一个模型辨识问题,其目前主要有两种解决思路,一是侧重于建模的精度,获得的模型结构复杂、模型项物理意义不明确,如多元单纯形B-样条法;二是侧重于建模的速度,获得的模型结构紧凑、易于使用,如逐步回归法及多元正交函数法(Multivariate Orthogonal Functions,MOF)。考虑到气动差量模型主要反映的是气动特性的天地差异性,其规律相比于飞行器的完整气动特性较为简单,故多采用第2种思路构建模型。其中MOF由于可解决参数共线性的影响,因此应用更为广泛。在传统MOF的基础上,文献[9]将样条因子引入模型优选程序,进一步提高了模型的非线性拟合能力;文献[10]为构建一个适用于全局的气动模型,引入频数准则对多条试验数据的气动模型项进行了统计分析。该方法提供了一种处理多条试验数据的思路,但其仅依赖模型项的频数作为准入标准,优选出的模型精度依赖于飞行试验数据的有效信息量。当信息量不足时,构建的模型不仅复杂,而且通用性不强。此外,MOF本质上基于最小二乘准则进行参数估计,因此要求组成回归因子的解释变量不包含任意误差,从而难以应用于测量精度不高的试验数据。综上所述,目前对于如何基于多条有效信息不足且测量精度不高的试验数据进行气动差量模型的辨识,并没有一种很好的解决方案。
针对第2个子问题,即完成对地面气动数据表的修正后,如何进一步量化气动修正模型的不确定性,目前鲜有研究。文献[11]在辨识差量模型的基础上,提出一种利用预测区间量化模型不确定度的方法,其基于概率的思想,能给出具有不同置信水平的不确定性区间。这种不确定性量化方法的预测效果依赖于训练集中试验数据的包络范围,当待估计状态位于有效包络范围内时,预测的误差带较为精准;反之,给出的误差带范围过大,无法满足精细化设计的需求。
本文主要贡献是提出一种适用于多条飞行试验数据的气动特性修正框架,实现了对地面气动模型及先验不确定性模型的修正。具体针对差量模型的辨识,首先为解决试验数据有效信息不足问题,一方面引入迭代思想改进了多元正交函数法,另一方面基于模型项的频数及可信度,构建了两个统计优选准则;然后为解决试验数据精度不高的问题,基于总体最小二乘思想,设计了适用于气动参数估计的定制化算法。针对模型的不确定度量化,首先基于不确定性理论,估计出气动修正模型的总偏差;最后基于贝叶斯估计准则,将地面的先验不确定性信息与估计的飞行不确定性信息进行整合,构建了一个新的不确定性模型。
1 问题描述
针对所研究的飞行器,目前在进行弹道仿真评估分析时,工程上多采用地面气动数据表及先验不确定性模型预示气动特性,分别给出任意状态下的气动系数值及其误差带范围[-,],表达式为
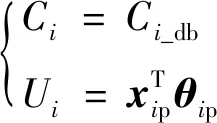
(1)
式中:_db为基于地面气动数据表插值所得的六分量气动系数;p为回归因子向量;p为先验参数,其值通常基于经验确定。
由于成本及试验条件限制,可直接获得的飞行试验数据主要有两类:一是弹载惯性测量系统(IMU)测量的视加速度及角速度;二是地面雷达测量的位置及速度。基于试验数据,结合实测的大气数据,完成弹道参数重建及气动系数换算,是进行气动辨识修正的前提。目前基于飞行后试验数据进行弹道重建的方法已较为成熟,根据是否考虑测量噪声的影响,分为随机性滤波平滑法和决定性输出误差法。本文基于文献[13]构建的飞行器动力学及运动学方程,应用文献[14]提出的滤波平滑框架(将扩展卡尔曼滤波与Fraser-Potter平滑器进行结合),以IMU测量数据作为输入数据、雷达测量数据作为观测数据,完成弹道重建,获得未直接测量的状态参数。然后计算气动系数的测量值_mea:
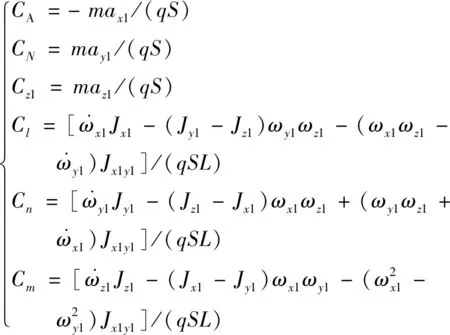
(2)

重建后获得的完整弹道数据,本文称之为低质量数据,其具有如下特点:试验缺乏主动激励,数据有效信息不足;飞行试验状态不同,数据相似性较低;传感器测量及弹道重建方法都存在误差,数据精度不高。本文研究目的就是基于多条低质量试验数据,完成对_db及的修正,从而提高气动特性的预示精准度。基于该目的,最终构建的气动特性修正框架如图1所示。

图1 气动特性修正框架Fig.1 Aerodynamic characteristic correction framework
2 气动差量模型辨识
地面气动模型修正的基本思路是:基于_mea与_db之间的残差_db,构建一个能够反映气动特性天地差异性的补偿差量Δ,并以此构建气动修正模型,表达式为
=_db+Δ
(3)
基于定常流动假设,Δ如下参量有关:
Δ=(,,,,,,,)
(4)
式中:为飞行马赫数;为攻角;为侧滑角;、及为等效控制舵偏角,分别对应俯仰、偏航及滚转;为飞行高度;为角速度,主要影响力矩系数。
由式(3)可得,气动模型修正的关键在于差量模型的辨识。为此本文提出一种针对低质量试验数据的气动模型混合辨识思路:首先引入迭代思想改进多元正交函数法,基于每一条试验数据完成差量模型的辨识;然后设计一种新的模型项优选准则,实现对多个气动模型的统计优选;最后采用总体最小二乘思想,解决参数的混合估计问题。
2.1 模型辨识方法
针对任意线性模型:
=+
(5)
式中:∈×1为响应向量,为观测样本点数;∈×1为与响应向量对应的观测噪声向量;∈×为解释矩阵,元素(=1,2,…,) 为回归因子,可由解释变量及其组合项组成,其通常为多项式,但为增强模型的局部建模能力,也可引入样条函数;∈×1为未知参数向量,可基于最小二乘法(Least Square,LS)进行估计,结果为

(6)
式中:为测量噪声方差,如果未知则可由残差进行估计:

(7)
多元正交函数法是一种基于最小二乘准则的模型结构优选方法,其应用流程归纳如下:
1) 生成正交回归因子。应用Gram-Schmidt程序处理原始回归因子,获得正交回归因子,表达式为

(8)

=
(9)
2) 正交模型参数估计。将代入式(5),产生新的回归模型,其中为对应于正交回归因子的参数向量。由于正交化后,为对角矩阵,故正规方程可以解耦,式(6)可简化为

(10)
3) 正交模型结构确定。正交回归因子模型项的具体选择以最小化预测平方误差(Predicted Squared Error,PSE)准则为基准,其由平均平方误差项(Mean Squared Fit Error,MSFE)及过拟合惩罚项(Overfit Penalty,OFP)组成:

MSFE+OFP
(11)
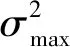

(12)
为进行回归因子的优选,需首先量化回归因子模型项的显著性。传统的MOF法定义回归因子减小MSFE能力作为显著性评估指标,经过推导可得,每一个正交回归因子的能力表示为
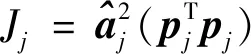
(13)
基于大小,按照由大到小的顺序引入回归因子。由于MSFE和OFP分别单调递减、递增,故PSE必然有一个全局最小值,从而可优选出具有个回归因子的模型结构,其兼顾了拟合能力和泛化能力。
4) 正交模型转化为原始模型。基于式(9),可将优选出的正交回归模型分解为具有物理意义的原始回归模型。由式(8)和式(13)可得,基于显著性大小引入正交回归因子的次序,直接影响了原始回归因子的个数,当某一靠后的正交回归因子具有较大的显著性时,其分解后将产生较多原始回归因子,从而使得优选出的原始模型不紧凑,难以应用于低质量的飞行试验数据。为此本文基于模型吝啬建模准则,提出迭代优化思路。
5)迭代优选回归因子。首先调节的大小,确定正交回归因子的期望个数;然后基于正交回归因子的显著性次序,调节原始回归因子的次序,重新进行步骤1)~4);继续迭代,直至正交回归因子与原始回归因子的数目接近。
基于迭代思想改进的多元正交函数法,可辨识出更为紧凑的模型结构。但由于试验数据有效信息不足,致使针对一条数据确定的气动差量模型,无法实现对地面气动特性全面、精准的补偿。解决这一问题的直接手段是统计分析,关键在于统计准则的构建。本文采用统计量表征模型项的可信度,然后结合模型项的频数,构建了两个统计准则,具体为

(14)
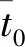
2.2 参数估计方法
经由统计分析获得气动差量模型后,接下来的重点就是基于多条试验数据,估计气动模型参数。目前主要有两种方式解决气动参数的混合估计问题,分别是基于最小二乘准则的一次性方法及基于贝叶斯准则的迭代方法。当没有参数的先验信息时,第一种方式更为简单实用。但是LS本质上要求回归变量不包含测量噪声,难以应用于低质量飞行试验数据。为此研究人员引入总体最小二乘法(Total Least Square,TLS)进行气动参数估计,当回归因子测量误差不可忽略时,TLS比LS具有更高的估计精度。
总体最小二乘法主要用来处理误差变量模型(Error-In-Variables,EIV),即同时考虑回归因子与响应变量误差的线性模型,其形式为
=(-)+
(15)
总体最小二乘问题的优化准则为
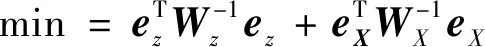
(16)
式中:∈×、∈×为相应噪声协方差矩阵;∈×1=vec(), vec(·)表示矩阵的拉直运算,其将矩阵按列重新排列成一个新的列向量。
总体最小二乘问题的求解方法取决于噪声矩阵的形式,噪声信息越多,参数估计精度越高,但计算过程也越复杂。具体应用于气动参数估计时,主要存在两个难点: ① 模型中部分回归因子,如常数项,是精确已知的,无法直接基于TLS思想进行处理; ② 回归因子和响应变量的噪声方差特性不同,不满足经典TLS方法的应用前提。
针对难点 ①,本文应用混合LS-TLS问题构型进行求解,即基于QR分解将数据矩阵进行分割,将混合问题转化为最小二乘估计和总体最小二乘估计两个子问题:

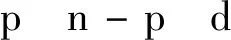
(17)
式中:∈×是由精确已知的回归因子组成的解释矩阵;∈×(-)中的回归因子包含测量误差;由于本文主要针对单响应变量,故=1;待估计参数=[,]可分别基于LS和TLS思想求解获得:
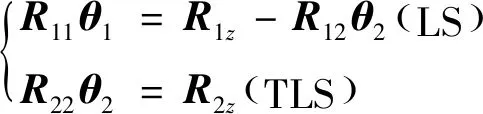
(18)
针对难点 ②,基于低质量数据特点,忽略噪声的自相关性及互相关性,即假设为对角矩阵且元素相等、=diag(,,…,)且∈(-)×(-)为对角矩阵;简化后采用广义总体最小二乘法求解,具体有两种计算手段,即数据缩放和广义的奇异值分解。数据缩放处理过程较为简便,其核心思想是基于权重特性=diag(,)将复合数据矩阵=[2]进行归一化,表达式为


(19)


(20)
式中:∈(-)×(-+1)为奇异值矩阵;、分别为左、右奇异矩阵;、分别是最后一列的最后一个元素、前-个元素。
完成对的估计后,代入式(18),应用LS便可实现对的估计,参数估计的协方差可由式(21) 进行统一计算:
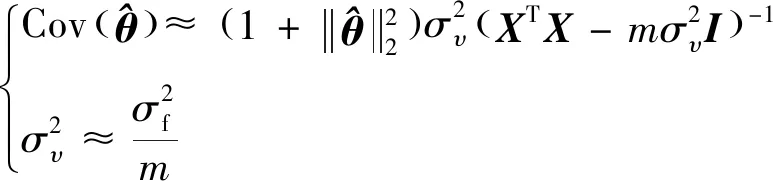
(21)
式中:为最小的奇异值。
3 不确定性模型修正
基于差量模型完成对地面气动系数的修正后,需重新量化修正模型的误差范围。本文在地面先验不确定性模型的基础上,提出了一种新的不确定度量化思路:首先基于不确定性理论,计算修正气动系数的总偏差;然后基于贝叶斯估计准则,应用气动总偏差校正先验不确定性模型。
3.1 不确定度量化
气动修正模型的总偏差Δ主要包括两部分: ① 测量气动系数与修正气动系数的残差_; ② 测量气动系数的测量误差_mea,表达式为
Δ=|_c|+|_mea|
(22)
式中:_=_mea-(_db+Δ);、为权重。
由于_mea是通过弹道重建获得而非直接测量,因此其测量误差可通过对重建过程进行不确定性分析计算。不确定性分析是研究重建参数可信度的一种常用手段,其通过研究重建过程的输入误差、模型误差及重建方法误差的传递影响,来量化重建输出参数的不确定性分布。对于弹道重建来说,当选定重建模型及方法后,重建过程的主要不确定性便是输入不确定性。输入不确定性又可分为随机不确定性和认知不确定性,本文分别采用概率法及区间分析法进行建模,具体特性如表1所示。
提取出不确定性因素后,接下来为量化输出的统计分布,需进行不确定性传递分析。不确定性传递主要以输出为对象,量化不确定性输入经过系统传递对输出的影响,具体传递方法的选择取决于不确定性输入的类型。由表1可得,弹道重建输入同时包含随机和认知不确定性,其属于混合不确定性传递问题。对于这种情况,目前应用最为广泛的是双层蒙特卡洛法,其基本思想是:认知不确定性参数在外层蒙特卡洛模拟中采样,随机不确定性参数在内层蒙特卡洛模拟中采样,统计结果由p-box图呈现。但对于弹道重建,如果直接应用双层蒙特卡洛法,需存储所有的打靶数据,并且需要对每一时间点的弹道参数进行手工处理以获得p-box图,处理程序较为繁琐。为此本文对双层蒙特卡洛法进行了简化,基于递推方式直接计算每一时间点处各弹道参数的均值和方差,具体步骤如下:

表1 弹道重建输入不确定性特性Table 1 Characteristics of input uncertainty in trajectory reconstruction
根据不确定性变量的模型,采样生成个样本点{a_,e_}1≤≤。其中和分别是随机不确定性向量和认知不确定性向量。假设服从高斯分布,由于是区间形式,没有概率意义,故假设服从均匀分布。然后统一采用随机采样法获得样本点。
基于弹道重建算法,计算每一个样本点的系统响应值(输出参数及六分量气动系数)的时间历程,{=[(),…,()]}1≤≤。


(23)

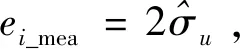
3.2 模型混合估计
气动修正模型的总偏差Δ侧重于表征由气动辨识引入的误差,称之为飞行不确定性;地面先验不确定性模型则侧重于表征由风洞试验及气动系数工程计算方式等引入的误差,称之为地面不确定性。为更精准地反映气动修正模型的误差特性,需同时考虑上述两类误差的影响。为此本文基于贝叶斯准则,利用Δ来校验地面不确定性模型的参数,其代价函数为


(24)
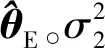

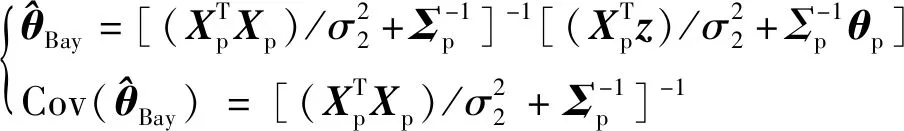
(25)
4 试验数据结果分析
某型飞行器迄今已积累了10条飞行试验数据,经由数据预处理及弹道重建后,可获得气动辨识所需的完整弹道参数及气动系数的时间历程。本文应用所提出的气动特性修正框架(图1)对重建数据进行处理,具体给出轴向力系数、法向力系数及俯仰力矩系数的修正结果。
4.1 气动修正模型
考虑到该型飞行器的飞行特点(速度快、空域广且飞行状态变化明显)及重建数据的低质量特性,难以直接辨识出一个适用于全局的气动差量模型。为此本文采用数据分割思想,选择飞行高度、攻角及侧滑角作为分割变量,将飞行包络分为4个区间,即高空小攻角小侧滑、高空大攻角小侧滑、中空小攻角大侧滑及低空大攻角大侧滑;然后分别在每一个区间内进行辨识,确定出局部差量模型;最后基于线性加权思想融合不同局部模型,实现模型在区间交界处的平滑过渡。
低空大攻角大侧滑段主要进行速度控制,机动程度高、气动特性差异显著,故本文重点针对该区间进行分析。选择一条飞行试验数据Y1,其在低空大攻角大侧滑段内的大气风场测量结果如图2 所示,高度、马赫数、攻角及侧滑角的重建结果如图3所示。

图2 风场测量结果Fig.2 Wind field measurement results

图3 弹道参数重建结果Fig.3 Trajectory parameters reconstruction results
随机选择8条试验数据作为训练集,进行气动差量模型的混合辨识。首先针对每一条试验数据,采用改进的多元正交函数法进行模型结构辨识,候选集中的模型项最高阶数设计为2;然后基于频数及可信度准则对辨识所得的8个模型进行统计优选。具体对于轴向力系数,应用迭代多元正交函数法处理Y1试验数据的结果如表2所示,对8个差量模型的统计优选过程如图4所示。

表2 单数据差量模型辨识结果Table 2 Single data difference model identification results
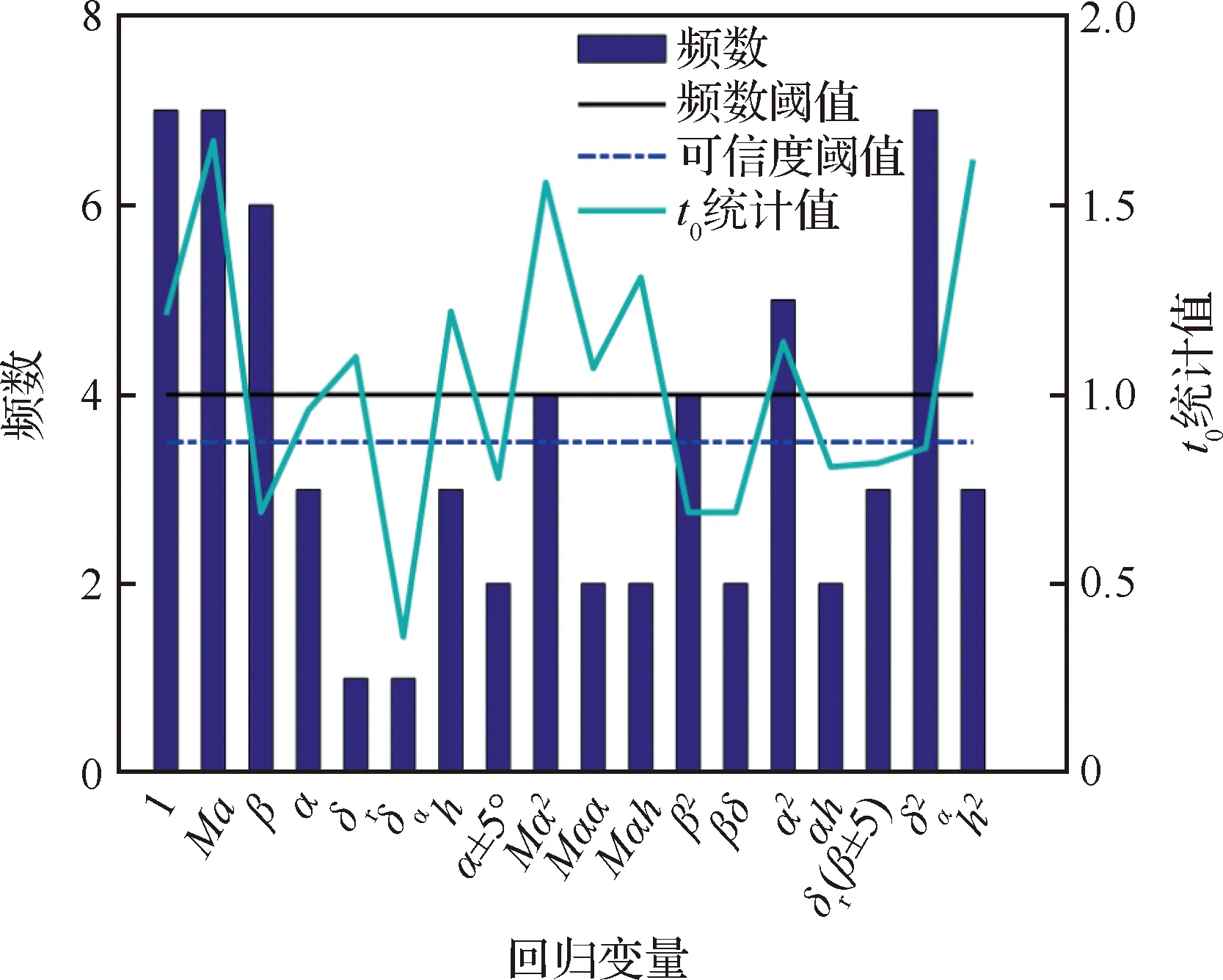
图4 差量模型统计优选结果Fig.4 Statistical optimization results of difference model
基于选定的Y1数据进行差量模型辨识时,设计=40,采用传统MOF计算,产生8个正交回归因子、15个原始回归因子;基于迭代的MOF,最终产生7个正交回归因子、8个原始回归因子,见表2。考虑到模型结构辨识的高实时性要求,采用LS方法快速估计参数,确定模型项的值。此外为降低试验数据的不同状态对模型项可信度的影响,本文将值进行了归一化处理。
进行统计优选时,本文设计频数阈值=4,可信度阈值=087,是训练集中试验数据数目的一半,是所有模型项可信度的均值。由图3可得,影响Δ的回归因子数目众多,且其频数及可信度差异较大。这是因为飞行试验缺乏有效激励,使得每一条试验数据只能反映出部分修正特性。如果试验数据中所有出现的影响项都作为Δ的回归因子,则会导致模型结构复杂,不便于使用且容易造成过拟合。因此本文重点关注训练集所反映出的主要气动特性修正规律,即确定具有普适性且可信度较高的回归因子。完成模型结构的构建后,应用总体最小二乘思想估计模型参数,获得3个气动系数的差量模型(式(26)),然后将其代入式(3)可得气动修正模型。
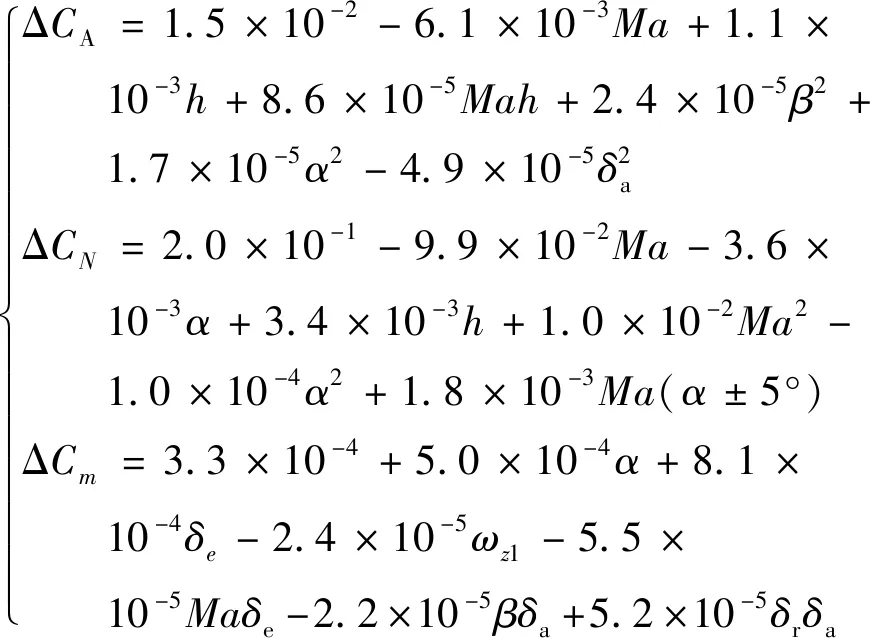
(26)
式中:(±5°)是样条回归因子,基本定义为

(27)
其中:是对应于回归因子的样条节点。考虑到飞行器的机动特性,本文只针对攻角和侧滑角,分别设计了两个节点,即5°和10°,然后将其作为候选模型项。
首先从气动设计角度,分析差量模型的物理意义。对于低空大攻角大侧滑段,基于地面气动数据表预示的气动系数主要有两方面的误差。一是气动系数的提供方法,其在工程中基于广义气动力近似公式计算,忽略了三通道的耦合性。该误差主要影响气动力矩系数,体现在差量模型中的和δ项;二是风洞试验数据的准度,主要考虑马赫数、雷诺数模拟不完全形成的天地差异和飞行器外形变化引起的气动系数偏差。前者体现在差量模型中的及相关因子,主要影响力系数;后者虽然对3个气动系数都有显著影响,但难以从理论上确定直接的关联量。考虑到差量模型中的剩余回归因子,如、、、和,都是相应系数的主要影响量,故将其作为外形变化引起的气动特性补偿量具有一定的合理性。
接着从模型拟合角度,分析差量模型的规律特性。在给定区间,气动差量模型对训练集数据测量残差的拟合效果见图5。差量模型的拟合精度采用均方根误差(Root Mean Squared Error,RMSE)进行衡量。Δ、Δ及Δ的RMSE分别是0.010 9,0.046 0和0.001 7。其中对于Δ,如果将样条项(±5°)替换为,则拟合误差增加到0.051 1,说明样条项能在一定程度上改善局部建模精度。由于差量模型的本质是表征一个共性的修正规律,故其拟合精度主要取决于所有试验数据的残差特性。具体来说,俯仰力矩系数的残差规律较为一致,优化出的Δ拟合精度最高,估计的补偿值整体上围绕0值波动;法向力系数残差的差异性最为显著,故Δ的拟合精度相对最低,其补偿值同样在0值附近波动;对于轴向力系数,多数试验数据具有正的残差特性,故Δ反映出一种接近常值的补偿特性,但由于数据6和7的存在,导致拟合精度不高。
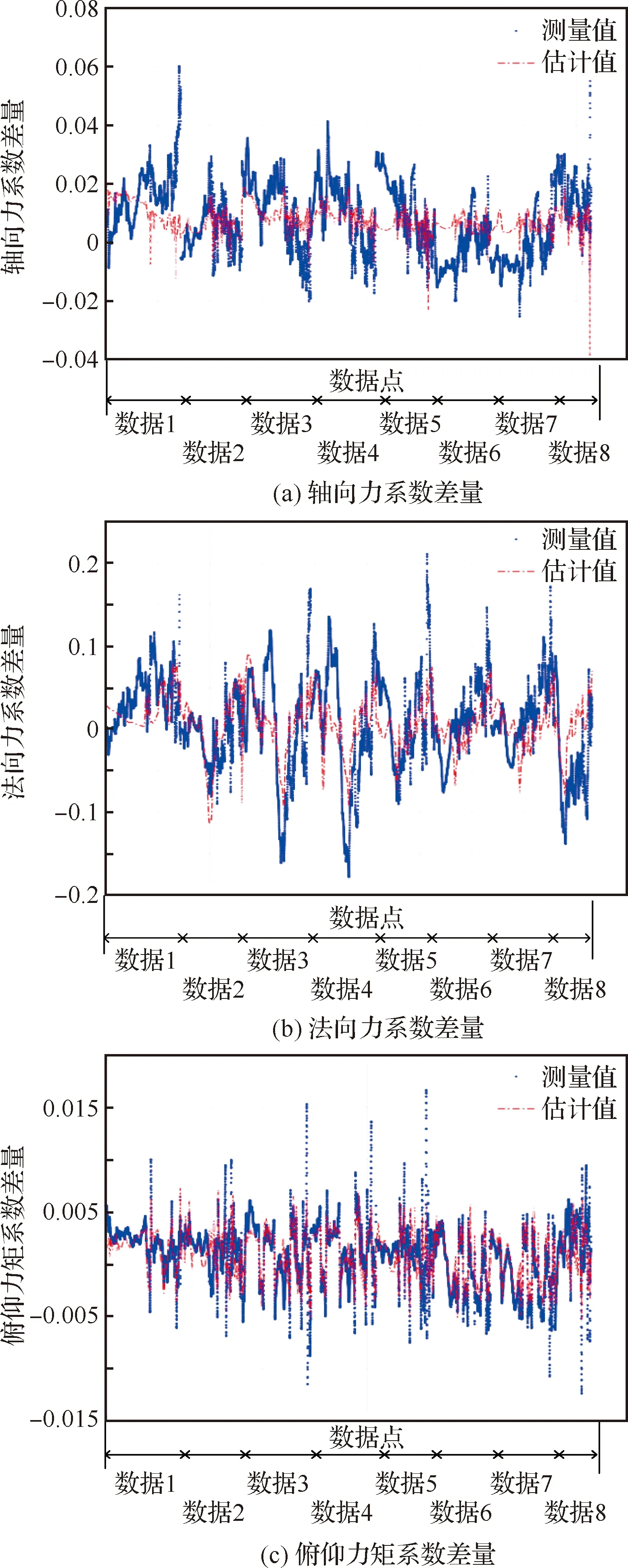
图5 差量模型在训练集的拟合效果Fig.5 Fitting effect of difference model in training set
4.2 气动不确定性模型
基于辨识所得的气动修正模型,再引入1条试验数据,校验地面先验气动不确定性模型。首先基于不确定性分析理论量化3个修正模型的总偏差Δ、Δ及Δ,相关结果如图6所示。

图6 修正气动模型的总偏差Fig.6 Total deviation of corrected aerodynamic model
基于确定出的Δ,应用模型混合估计方法校正先验气动不确定性模型,相关结果如表3所示。先验不确定性模型,是由设计人员基于气动系数的特性及工程经验进行定制化设计而得,不同的模型包含不同的回归因子,模型结构较为简单。大量试验表明,仅改变原模型参数,难以提高不确定性模型的精准度。为此首先对已有的先验回归因子进行整合,然后又引入了两个新的变量及,最终构建一个通用的不确定性模型结构。

表3 不确定性模型修正结果Table 3 Correction results of uncertainty model
对于俯仰力矩系数,本文给出不确定性模型修正前后的对比结果。图7(a)给出的是先验不确定性模型确定的误差带范围对原残差_db的包络特性,可见误差带整体安全余量较大、局部余量不足,即精细度不满足要求、可靠性仍有不足;图7(b)反映的是先验误差带对修正模型残差_的包络情况,经过气动差量模型的补偿后,不再有超出误差带的测量点,即提高了可靠性,但误差范围仍较为宽泛;图7(c)给出了气动模型及不确定模型的综合修正结果,其在保持高可靠性的基础上,前15 s的误差带范围有显著缩小,即进一步提升了精细程度。
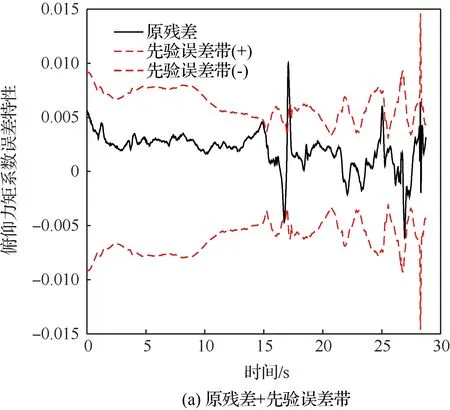
图7 气动误差带对比分析Fig.7 Comparative analysis of aerodynamic error band
4.3 模型确认
最后基于1条未使用的试验数据,进行气动修正模型及气动不确定性模型的确认。具体针对每一个气动系数,首先给出3种方式计算所得的气动系数值,分别是基于地面气动数据表的插值方法、基于试验测量数据的换算方法及基于修正模型的预示方法;然后对模型修正效果进行对比分析,分别给出“地面气动数据表+先验不确定性模型(方式1)”“气动修正模型+先验不确定性模型(方式2)” “气动修正模型+修正不确定性模型(方式3)”的预测特性,相关结果如图8~图10所示。
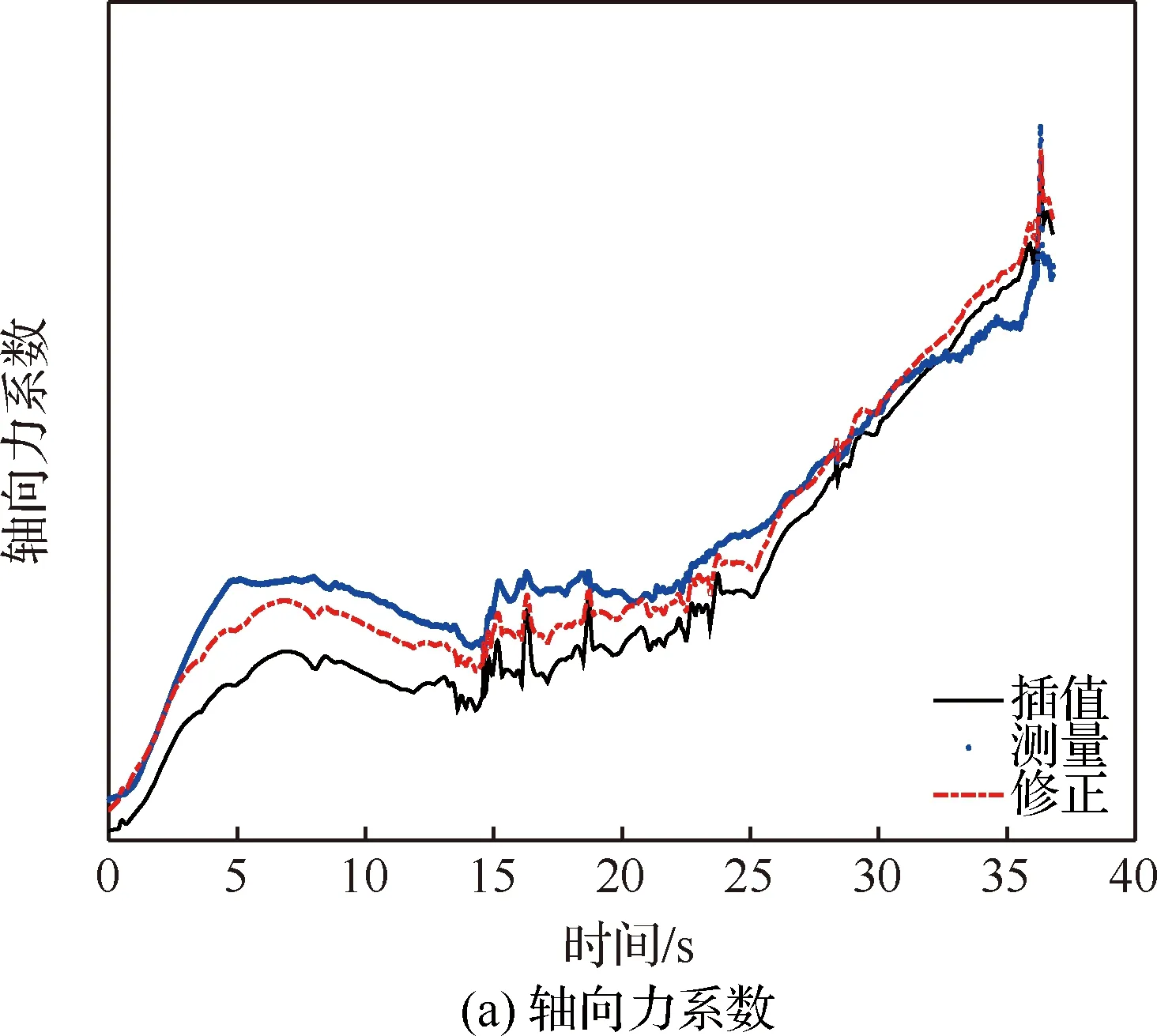
图8 气动系数预测值Fig.8 Prediction value of aerodynamic coefficients
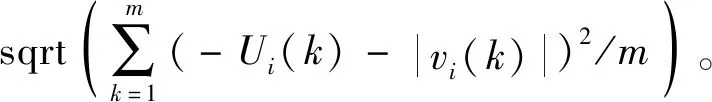
由图8~图10和表4可得,经过差量模型的补偿修正后,测量残差具有不同程度的减小,说明气动修正模型可改善气动系数的预示精度;“气动修正模型+先验不确定性模型”预示方式具有最少的误差带外测量点数,即气动修正模型也可提高气动预示的可靠性;气动系数经由差量模型修正后,采用修正不确定性模型确定的气动误差带,具有最小的剩余安全裕度,反映出修正不确定性模型的高精细度。综合来看,“气动修正模型+修正不确定性模型”预示方式相比于“地面气动数据表+先验不确定性模型”方式,可以有效提升气动特性预示的精准度,从而能够满足新型飞行器精细化气动设计的需求。
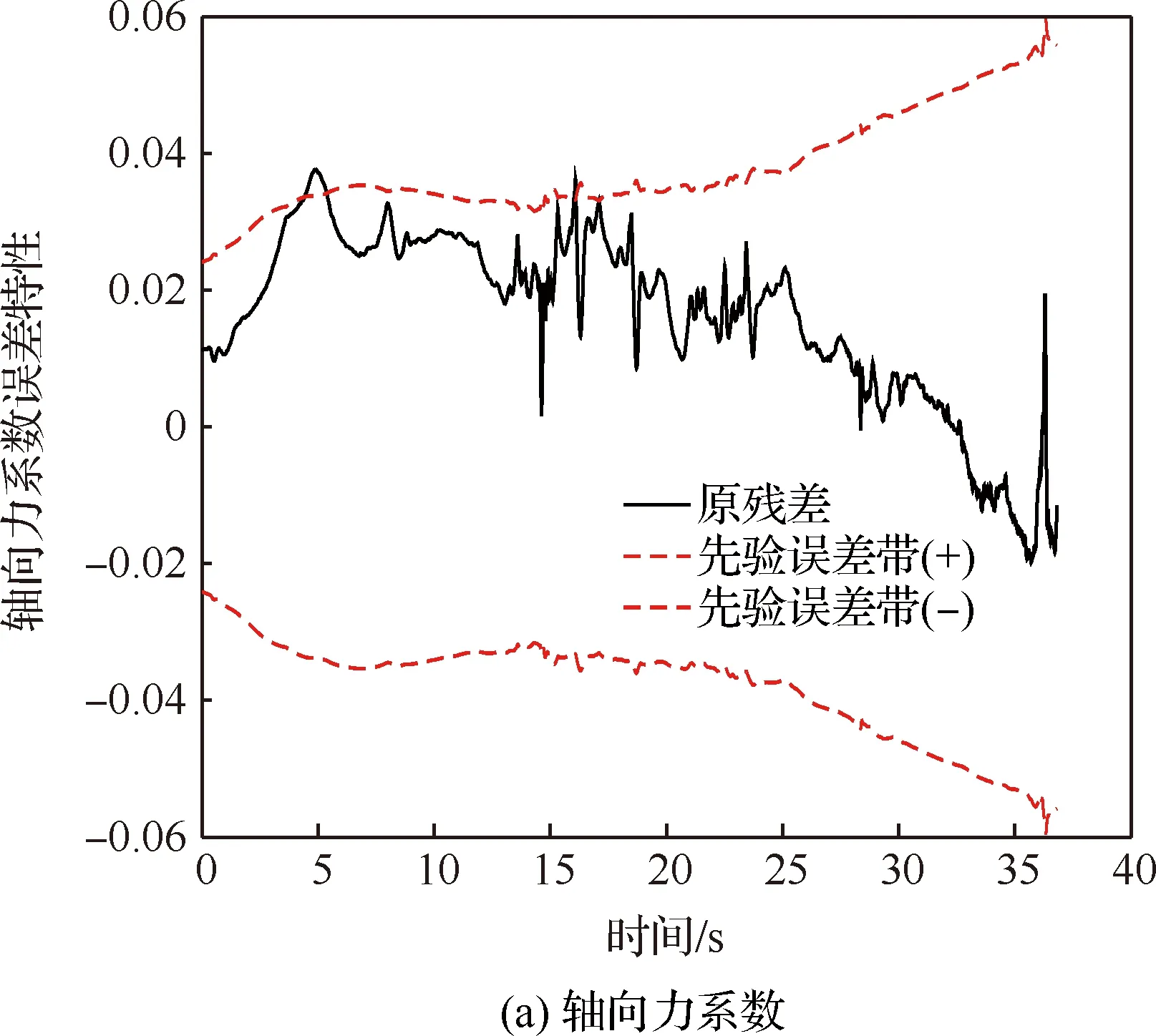
图9 原残差+先验误差带Fig.9 Original residual+prior error band
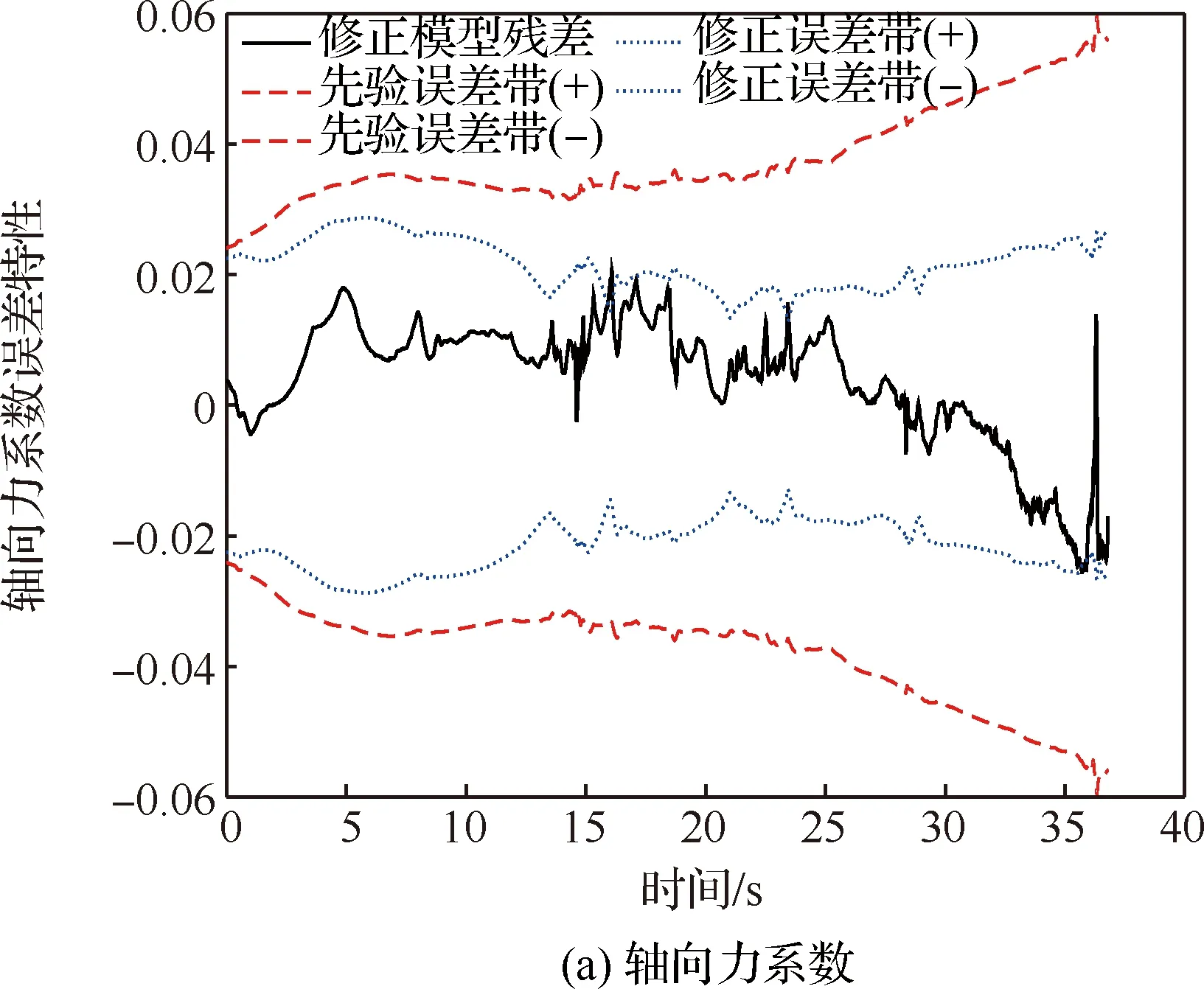
图10 修正前后误差带对比Fig.10 Comparison of error bands before and after correction

表4 不同气动特性预示方式对比结果Table 4 Comparison results of different aerodynamic characteristic prediction methods
5 结 论
本文提出一种适用于多条低质量飞行试验数据的气动特性修正框架。针对某型飞行器,重点在低空大攻角大侧滑段对地面气动预示特性进行了修正,具体结论如下:
1) 相比于地面气动数据表,气动修正模型预测的气动系数更接近测量的气动系数,即差量模型能够补偿一定的地面预示误差,提高气动系数的预示精度。
2) 气动修正模型结合先验不确定性模型具有最高的预测可靠性,确定的气动误差带具有最少的误差带外测量点,说明差量模型的补偿也能提高预示的可靠性。
3) 气动修正模型结合修正的不确定性模型能够给出精细度最高的气动误差带,其预示可靠性虽低于“气动修正模型+先验不确定性模型”方式,但高于“地面气动数据表+先验不确定性模型”方式,从而有效地提高了气动设计的精准度。
