机器人铣削系统精度控制方法及试验

2022-07-04李宇飞田威李波张楠

航空学报 2022年5期

李宇飞，田威，李波,*，张楠

1. 南京航空航天大学机电学院，南京 210016

2. 西门子(中国)有限公司, 北京 100102

新一代航空航天器尺寸越来越大，一体化复杂结构占比提高，传统数控机床难以适应大尺寸复杂部件的加工与装配需求。工业机器人凭借其高柔性、低成本的优势，正快速取代人工作业，成为智能化制造装备中不可缺少的部分。采用工业机器人对该类零件进行钻孔、铣削加工是提高大尺寸复杂部件装配效率，提高航空航天器研制水平的有效途径。

然而，工业机器人由于其开式链结构的特点，刚性仅有机床的1/50～1/20，定位精度相较于机床低1～2个数量级。目前，国内外相关企业与科研机构已经通过精度补偿方法将机器人的绝对定位精度提高到±0.5 mm以内，轨迹精度提高到±0.35 mm，成功实现了工业机器人在航空航天自动钻铆和铺丝铺带等方面的应用，但对于负载变化较大，精度要求更高的金属铣削领域，仍需要进一步提高重载机器人的定位与轨迹精度，以实现航空航天大尺寸复杂部件的机器人高精度加工。

对于工业机器人铣削作业及其精度控制的研究自20世纪90年代就已经开始。然而，现有的机器人铣削系统仍大多应用于快速原型技术中，机器人在对油泥、树脂等材料进行铣削时铣削力较小，因此铣削精度接近机器人静载轨迹精度，能够满足快速原型技术的精度要求。但使用机器人对金属材料进行铣削时，铣削力较大且变化难以预测，严重影响了机器人的轨迹精度。因此，部分学者为降低铣削力对机器人的影响，研究了铣削力的预测方法和机器人的刚度补偿技术。

达姆施塔特工业大学的Abele等研究了机器人铣削过程的刚度建模与离线刚度补偿方法，对机器人关节处分别建立了单自由度和三自由度的柔性模型，并通过Dexel模型预测了铣削力，从而补偿了机器人关节处的柔性变形，将机器人三轴铣削时和方向的轨迹误差降低到1.5 mm。由于机器人的铣削力难以精确预测，对铣削力进行实时测量可以进一步提高机器人刚度补偿的效果。Wang等在机器人末端安装了六维力传感器，结合ABB机器人系统的力控开发包和机器人关节的定刚度模型，实现了柔性变形的实时补偿，将150 mm×50 mm面积内的单刀铣削平面度误差降低到了0.1 mm。Pan和Zhang也采用ABB机器人的力控包进行了实时的铣削力补偿，最终将发动机缸盖的铣削精度提高到了0.4 mm。Lehmann等通过对机器人铣削力和受力变形的离线标定实现了在机器人工具坐标系下的实时刚度补偿，该方法避免了对机器人刚度的建模，并且由于计算简便，可以在机器人的每个插补周期内均进行一次补偿。此外，为了不依赖于机器人铣削力的预测或测量，焦嘉琛、Gonul等依靠机器人的冗余自由度对机器人铣削过程的姿态进行了刚度优化，降低了机器人在铣削时的柔性变形。

机器人的柔性主要来源于机器人关节，因此，对机器人关节处进行刚度建模，并依据铣削力计算柔性变形的补偿方法在一定程度上提高了机器人的铣削精度，但对于机器人运动学参数误差、关节齿隙等因素导致的轨迹误差则无法补偿。为此，部分学者采用外部测量设备对机器人位姿进行了实时测量和全闭环补偿。Schneider等将KUKA KR125机器人的原有控制系统改造为倍福TwinCAT CNC系统，使用尼康K600光学测量装置对机器人进行实时位姿补偿，测量频率为1 kHz，精度±90 μm，最终在钢毛坯上将0.5 mm深，70 mm直径圆形沟槽的铣削精度提高到平均63 μm(最大0.35 mm)。Moeller等研发了一套基于西门子840Dsl数控系统的MABI机器人移动铣削系统，采用激光跟踪仪进行全闭环补偿，在树脂材料上铣削的沟槽精度达到了±0.25 mm。除了对机器人位姿进行实时测量，Olofsson等研发了一种三维压电驱动机构，将电主轴置于该机构上，通过激光位移传感器对机器人末端携带的待加工件进行实时测量，机器人和三维压电驱动机构共同补偿铣削误差，端面铣削和侧面铣削的精度均达到了±12 μm以内。Abele等对机器人加工过后的零件进行了三维测量，进一步修正了离线刚度补偿在机器人Z轴方向补偿精度的不足。

综上所述，机器人高精度铣削的研究仍处于起步阶段，基于铣削力的刚度补偿对提高机器人铣削精度的效果有限；现有的全闭环测量和补偿方法容易导致测量靶标受零件遮挡，降低了机器人铣削系统的柔性；测量加工后的零件再补偿的方法降低了系统的加工效率，且不适用于加工多种类、小批量的航空航天复杂结构部件；固定电主轴的铣削模式则大幅降低了机器人铣削系统的加工范围。因此，急需一种不依赖于外部测量装置，且能够实时补偿机器人铣削系统加工精度的控制方法。

针对上述不足，搭建了一种采用数控系统控制的工业机器人铣削系统。利用数控系统的二级编码器接口，可以在机器人的每个关节加装第二测量系统，并通过对数控系统进行二次开发编写机器人在笛卡尔空间的精度补偿算法，解决了KUKA机器人自带驱动器与控制器底层控制端不开放的问题。机器人铣削系统采用关节空间-笛卡尔空间分级精度补偿方法，通过离线标定和在线实时补偿提高了机器人的重复定位精度、绝对定位精度和轨迹精度。在铣削试验部分，复合材料舱段体积大，材料难加工，且精度要求高。试验结果表明，分级精度补偿方法将机器人铣削精度提高到了0.22 mm，使其满足了航空航天零部件的加工精度要求。

1 机器人铣削系统及其精度控制方法

1.1 机器人铣削系统组成

机器人铣削系统由KUKA KR500 R2830MT机器人本体、数控系统、雷尼绍RESOLUTE不锈钢直线光栅尺以及睿克斯电主轴组成。机器人本体的6个电机以及末端电主轴由伺服驱动器直接控制，光栅尺直接粘贴在机器人关节处，作为各轴电机的第二测量系统。整个系统的拓扑结构如图1所示。

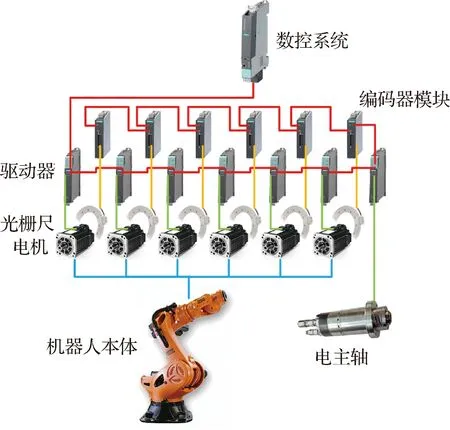
图1 机器人铣削系统硬件拓扑图Fig.1 Hardware topology of robot milling system

采用数控系统代替KUKA机器人原有控制器KRC4，可以实现关节空间-笛卡尔空间的分级精度补偿。其中关节空间的补偿主要依靠光栅尺实现，由于光栅尺直接测量机器人关节处减速器输出的真实转角值，以光栅尺作为第二测量系统可对机器人关节齿隙、关节柔性造成的关节转角误差进行实时补偿。由于机器人的定位误差在空间中具有相似性，可以对机器人预先进行误差标定，并采用线性无偏最优估计或空间反距离加权算法进行笛卡尔空间定位误差的补偿。在关节转角准确的前提下，笛卡尔空间的补偿方法进一步修正了由于其他运动学参数误差和机器人连杆柔性导致的定位和轨迹误差。

1.2 机器人关节空间精度补偿策略

由于雷尼绍RESOLUTE不锈钢直线光栅尺只能提供沿光栅尺进行直线运动的位移距离，因此，在测量机器人关节转角时，需要将不锈钢直线光栅尺粘贴在机器人各关节精加工的圆柱面上，从而最大程度地保证直线光栅尺测量结果映射到关节转角的准确性。各关节光栅尺的安装情况如图2所示，图中A1～A6表示机器人关节轴编号，即1号关节轴到6号关节轴。

图2 各关节光栅尺安装Fig.2 Installation of grating scales for each joint

当光栅尺安装到机器人各关节后，需要对光栅尺进行标定。假定采用测量设备对机器人某关节转角范围的标定结果为，光栅尺测量起始点为，终止点为，如图3所示。若光栅尺在这两点的读数为和，则光栅尺读数与角度的比例系数为

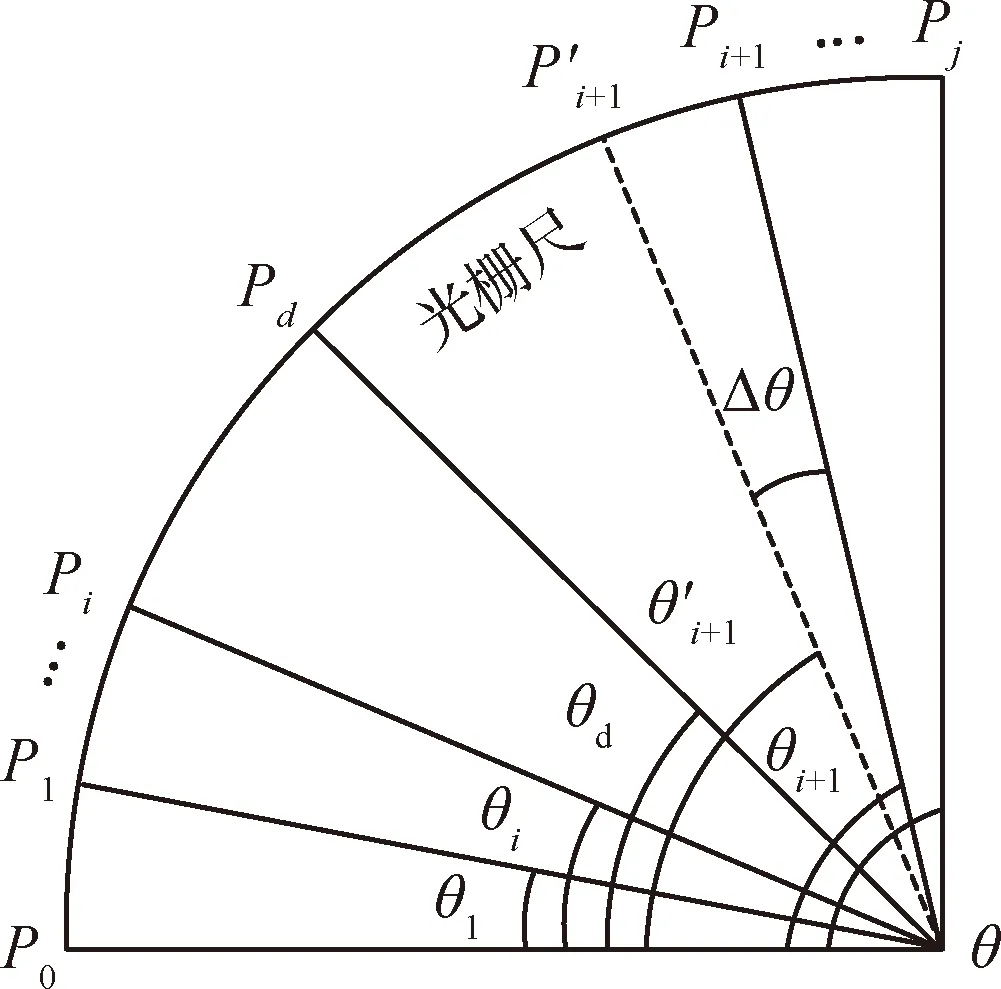
图3 光栅尺标定原理图Fig.3 Calibration schematic of gratingscale

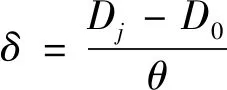
(1)

将比例系数输入到数控系统中，便可启用光栅尺作为第二测量系统，对机器人关节转角进行实时补偿。然而，如果在整个关节的运动范围均采用固定分辨率，会引入光栅尺受手工粘贴和圆柱面径向跳动导致的转角测量误差。因此，需要通过数控系统的螺距补偿功能对光栅尺与转角的映射关系进行进一步的细化和线性补偿。螺距补偿功能可在机器人某关节转角范围内平均分布-1个点～-1，～-1为对应点位光栅尺的读数。以+1点为例，其相对于负限位点的理论角度为+1，采用设备对该关节真实转角的实测值为′+1，则待补偿点的真实转角值为

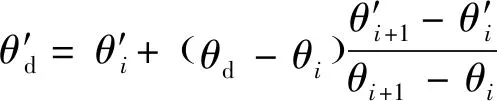
(2)

式中：′为点角度的实测值，由于光栅尺读数与关节理论转角相对应，式(2)可改写为

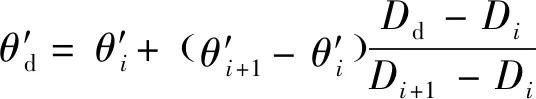
(3)

因此，只需要将每个螺距补偿点位的实测转角输入数控系统，便可实现对关节转角范围内所有点的补偿，提高机器人关节转角的定位精度。

1.3 机器人笛卡尔空间精度补偿策略

由于机器人在笛卡尔空间中的绝对定位误差具有相似性，可通过测量点的误差对待补偿点的误差进行预测。为方便测量过程和误差预测，可将机器人采样空间划分为一系列立方体网格，则机器人运动范围内的任意一个待补偿点必然处于某个立方体内或几个立方体的相交线/面上。如图4所示，立方体网格的8个顶点为(=1,2,…,8)，对于不处于采样空间边缘的立方体，定义其顶面、正面和左面，以及、和三条棱属于该立方体，其余面和棱归属于与之相邻的其他立方体。定义立方体网格各顶点的理论坐标为(,,)，测量得到的实际点位坐标为(′,′,′)，各顶点的定位误差为理论值与测量值的差，定义为(Δ,Δ,Δ)。则待补偿点的定位误差预测方法为

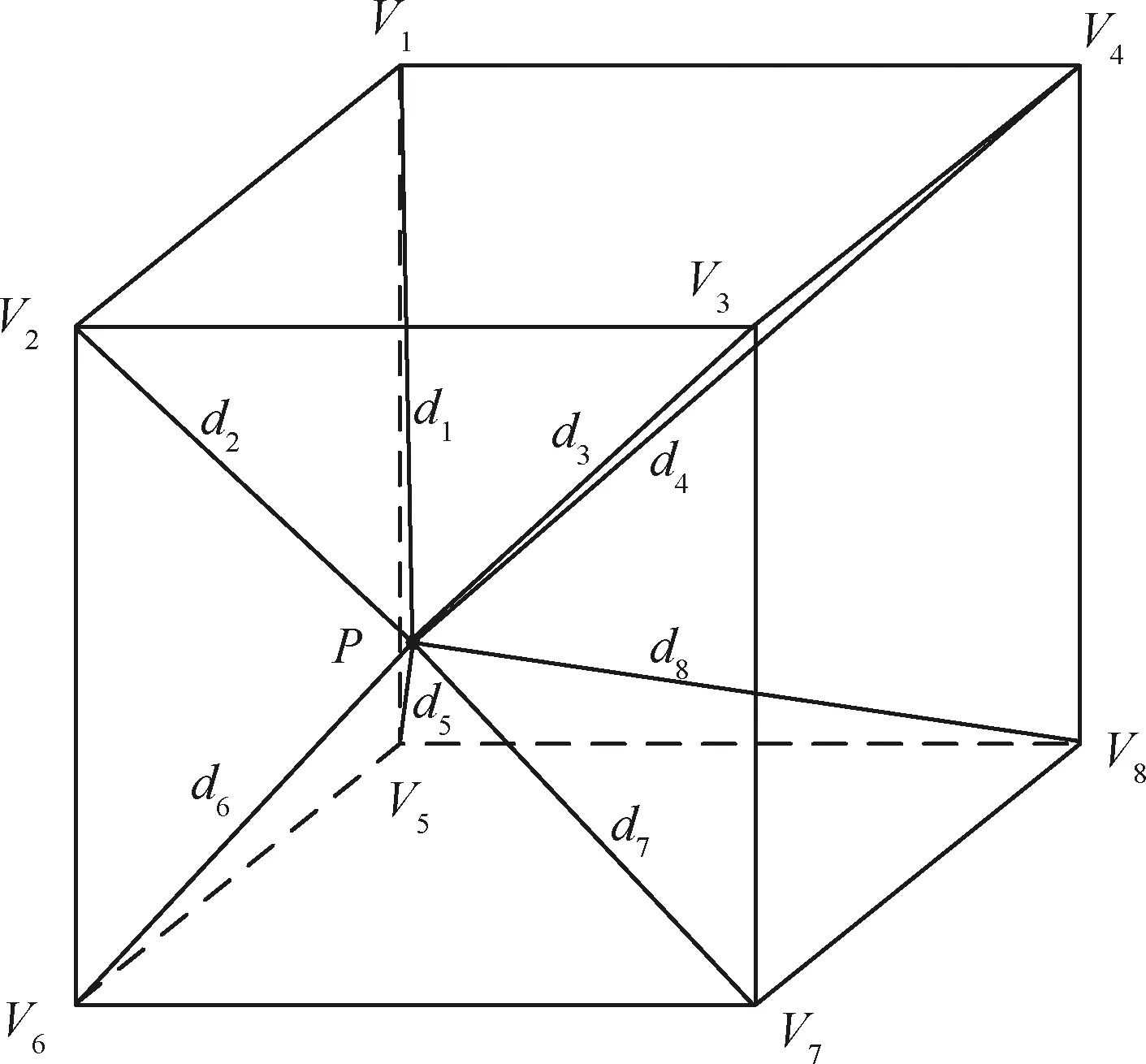
图4 空间立方体网格Fig.4 Diagram of spatial grid

1) 首先计算各顶点定位误差对待补偿点误差的权值：

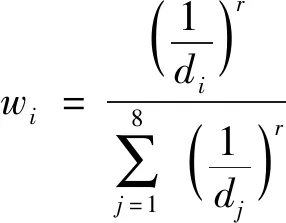
(4)

式中：为点定位误差的权值;、为各顶点到待补偿点的距离;为加权幂指数，取值范围通常为1～3。为实现空间定位误差的平滑过渡，在本文实验的计算过程中取1。

2) 根据计算出的权值大小，在3个方向上对待补偿点误差分别进行加权平均，预测待补偿点的定位误差：

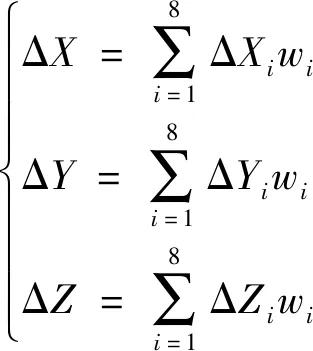
(5)

3) 采用预测的误差修正待补偿点的理论坐标(,,)，控制机器人到达修正后的坐标位置(′,′,′)，完成点位/轨迹的补偿：

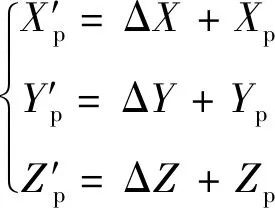
(6)

反距离加权(Inverse Distance Weighted, IDW)精度补偿策略如图5所示。

笛卡尔空间精度补偿策略是通过对数控制系统进行二次开发实现的。首先，通过数控系统中的子程序模块和用户自定义参数将数控加工程序中的期望点位传递至精度补偿程序中；随后，精度补偿程序判断期望点位所处的空间网格，并调用该网格的误差参数，采用图5中的反距离加权精度补偿策略对该点位进行补偿；最后，精度补偿程序将补偿后的点位传递至子程序模块，控制机器人运动至补偿后的点位，完成对数控加工程序的精度补偿，补偿原理如图6所示。

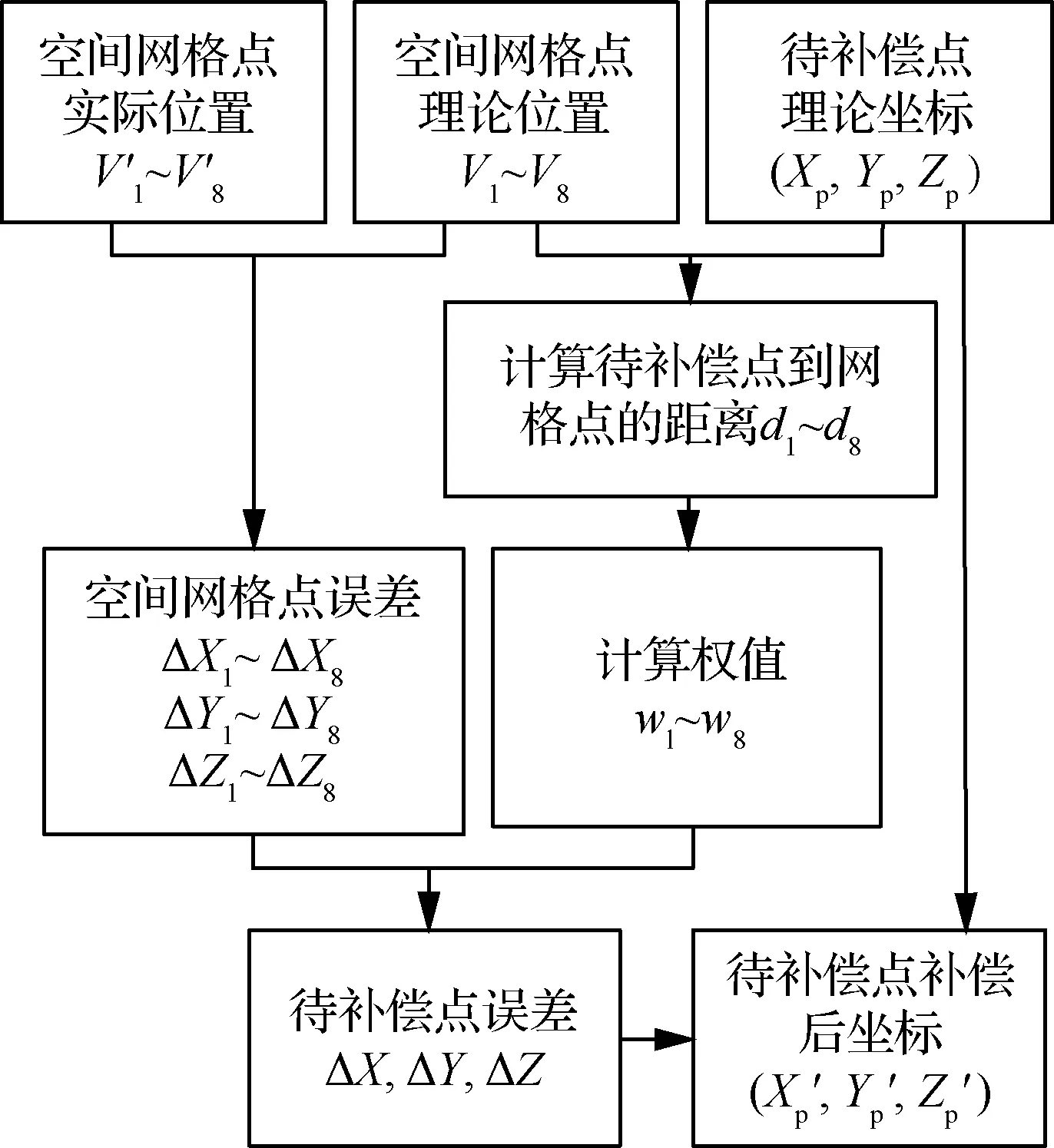
图5 反距离加权精度补偿策略示意图Fig.5 IDW precision compensation strategy

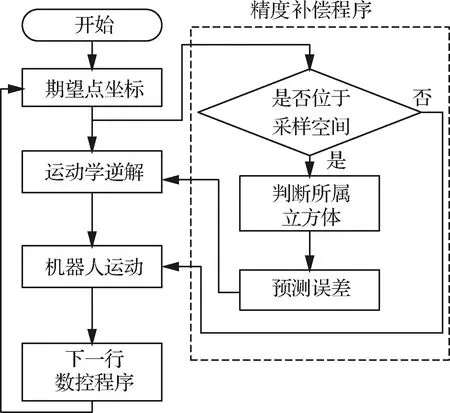
图6 笛卡尔空间精度补偿原理示意图Fig.6 Schematic of Cartesian space accuracy compensation principle

为了在铣削过程中实现最优的补偿效果，需要尽可能地缩小数控加工程序中控制点位的间距，即在铣削路径上尽可能多地添加补偿后的点位，从而提高轨迹精度。为此，采用离线编程软件对工件的加工过程进行编程和仿真，如图7所示。将待加工筒段的圆弧离散成1 452段直线，控制机器人沿控制点位进行直线运动，并对每个点位进行精度补偿，即可实现机器人整个铣削过程的轨迹补偿。

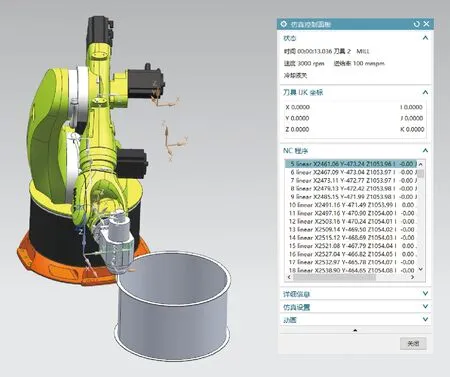
图7 离线编程与数控程序生成界面Fig.7 Offline programming and NC program generation interface

2 机器人静载精度试验

由于现有的机器人航空航天加工装备多为自动钻铆装备，对静载下的重复定位精度和绝对定位精度要求较高。因此，为了验证本文所采用的分级精度补偿方法对机器人钻铆系统的通用性以及对机器人本体性能的提升效果，设计了机器人静载状态下的重复定位精度、绝对定位精度和轨迹精度的对比试验。其中重复定位精度和轨迹精度均采用国家标准中所规定的测量路径和循环次数，但由于该标准中对机器人绝对定位精度的测试点位较少，难以表现机器人在整个工作空间中的最大绝对定位误差。因此，采用在工作空间中随机采样300个点的方式进行绝对定位精度测试。机器人的定位误差可分为几何误差与非几何误差，分级补偿方法补偿了机器人的几何误差及部分非几何误差，剩余的非几何误差来源主要有连杆变形、热效应等因素，可以认为是随机误差。因此，可以计算误差的平均值、最大值以及标准差，依据正态分布的3准则判断试验结果的可信度。

2.1 重复定位精度补偿试验

机器人铣削系统如图8所示，使用Leica AT960激光跟踪仪对机器人末端的靶标球位置进行测量。根据各关节的限位条件将机器人的工作空间规划为600 mm×1 200 mm×600 mm的长方体，并划分成边长为100 mm的立方体网格。

图8 机器人铣削系统Fig.8 Robot milling system

对总共637个顶点进行误差采样，并汇总成432种点位分布条件，在精度补偿和数控系统子程序中按照1.3节的补偿方法进行编程。

首先对机器人的重复定位精度进行对比测试。由于机器人的重复定位精度主要依赖于关节转角的重复精度，笛卡尔空间精度补偿策略对提高机器人的重复定位精度没有意义。因此，本小节主要对比关节空间精度补偿策略对机器人重复定位精度的提升效果。测试方法为令机器人末端在规定立方体内沿指定路径循环到达指定对角面上的5个点，如图9中带箭头的虚线所示，循环次数为30次。测量结果见表1。

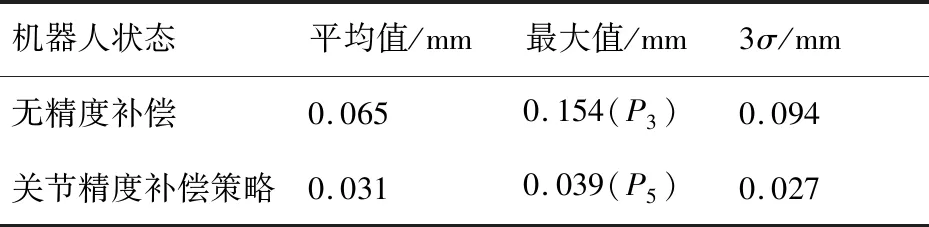
表1 机器人重复定位精度Table 1 Robot repetitive positioning accuracy

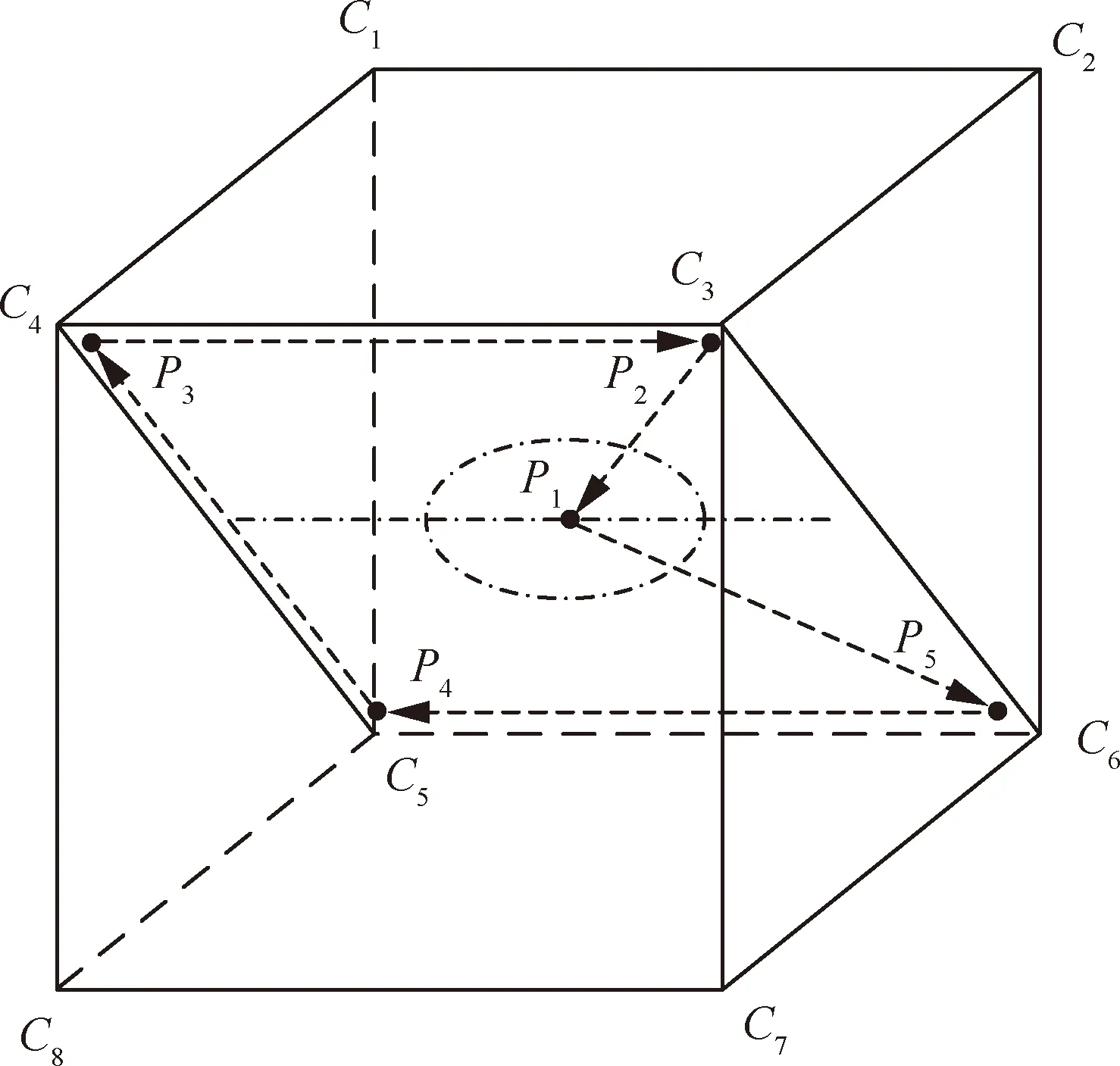
图9 机器人重复定位精度/轨迹精度测试轨迹Fig.9 Test trajectory of robot repeated positioning accuracy & trajectory accuracy

由测量结果可以看出，关节空间精度补偿策略将机器人重复定位精度的平均值提高了52.31%，最大值提高了74.68%。同时，关节空间精度补偿策略也提高了机器人在不同点位时重复精度的稳定性，补偿前的最大重复定位误差为0.154 mm，出现在点，较平均值高出136.92%，补偿后的最大重复定位误差较平均值高出25.81%，补偿前后机器人重复定位精度的稳定性提高了81.15%。然而，精度补偿后的机器人重复定位误差分布结果并不符合正态分布的3准则，最大误差超过了平均值±3的范围，推测可能是由于激光跟踪仪的测量不确定度为0.015 mm，对于机器人重复定位精度的测量受仪器不确定度影响较为严重，需要采用更高精度的仪器进行测量。

2.2 绝对定位精度补偿试验

机器人的绝对定位误差可分为运动学误差和非运动学误差，运动学误差主要体现在机器人连杆参数的制造误差和关节转角的控制误差，非运动学误差包括关节与连杆柔性、负载变化、热效应等因素。机器人铣削系统的连杆参数已经预先采用激光跟踪仪完成标定并输入到数控系统内，机器人关节转角的控制误差与柔性可通过关节空间精度补偿策略对其进行修正，其余非运动学误差以及测量过程产生的坐标系误差可通过笛卡尔空间精度补偿策略进行修正。由于笛卡尔空间的补偿策略是对关节空间补偿策略的补充，在进行绝对定位精度对比试验时，将分别测量机器人本体、采用关节空间补偿策略以及采用关节空间-笛卡尔空间分级精度补偿方法的绝对定位精度。

在机器人工作空间随机挑选300个点，机器人的绝对定位精度测量结果如表2所示。

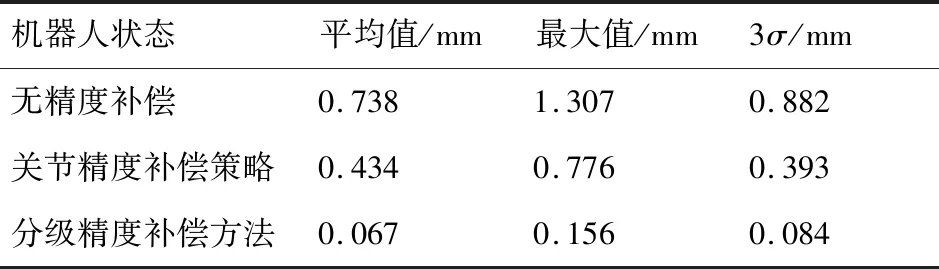
表2 机器人绝对定位精度Table 2 Robot absolute positioning accuracy

由测量结果可以看出，关节空间精度补偿策略将机器人绝对定位精度的平均值与最大值分别提高了41.19%和40.63%，分级精度补偿方法在关节空间补偿策略的基础上将绝对定位精度的平均值与最大值再次提高了84.56%和79.9%。因此，关节空间精度补偿策略和笛卡尔空间的精度补偿策略对提高机器人的绝对定位精度均有着至关重要的作用，将二者结合的分级精度补偿方法最终将机器人绝对定位精度的平均值与最大值提高了90.92%和88.06%。同时，机器人在不施加精度补偿算法时测得的最大定位误差相较于3

准则的计算结果较低，说明挑选的300个点位并没有覆盖机器人定位误差最大的点，但补偿后的精度测试结果均符合3准则，说明补偿后的测试结果可以反映机器人在整个工作空间内的精度特性，测试结果可信度高。

2.3 轨迹精度补偿试验

机器人轨迹精度的测试方法为令机器人末端在规定立方体内分别沿以中心点为圆心的圆周和经过中心点的直线运动，如图9中点画线所示，圆周直径为300 mm，直线长度为1 000 mm，轨迹的循环次数为10次，机器人的运动速度为2 000 mm/min。测试结果如表3、图10和图11所示。

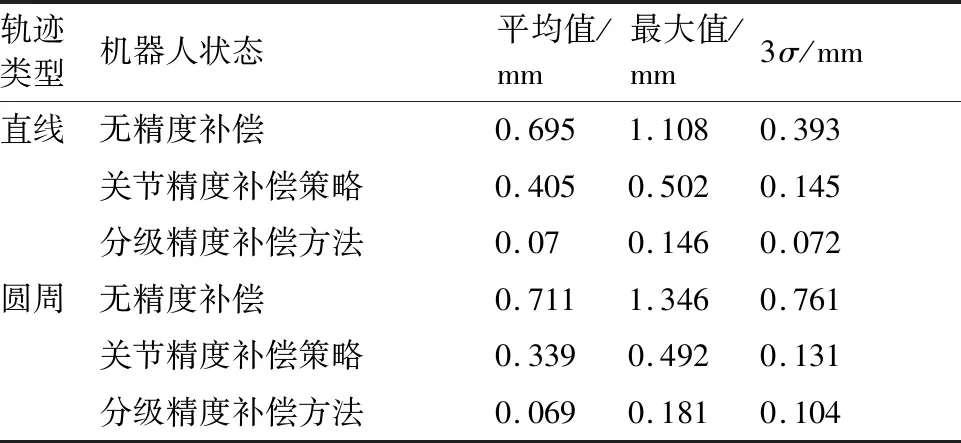
表3 机器人轨迹精度Table 3 Robot trajectory accuracy

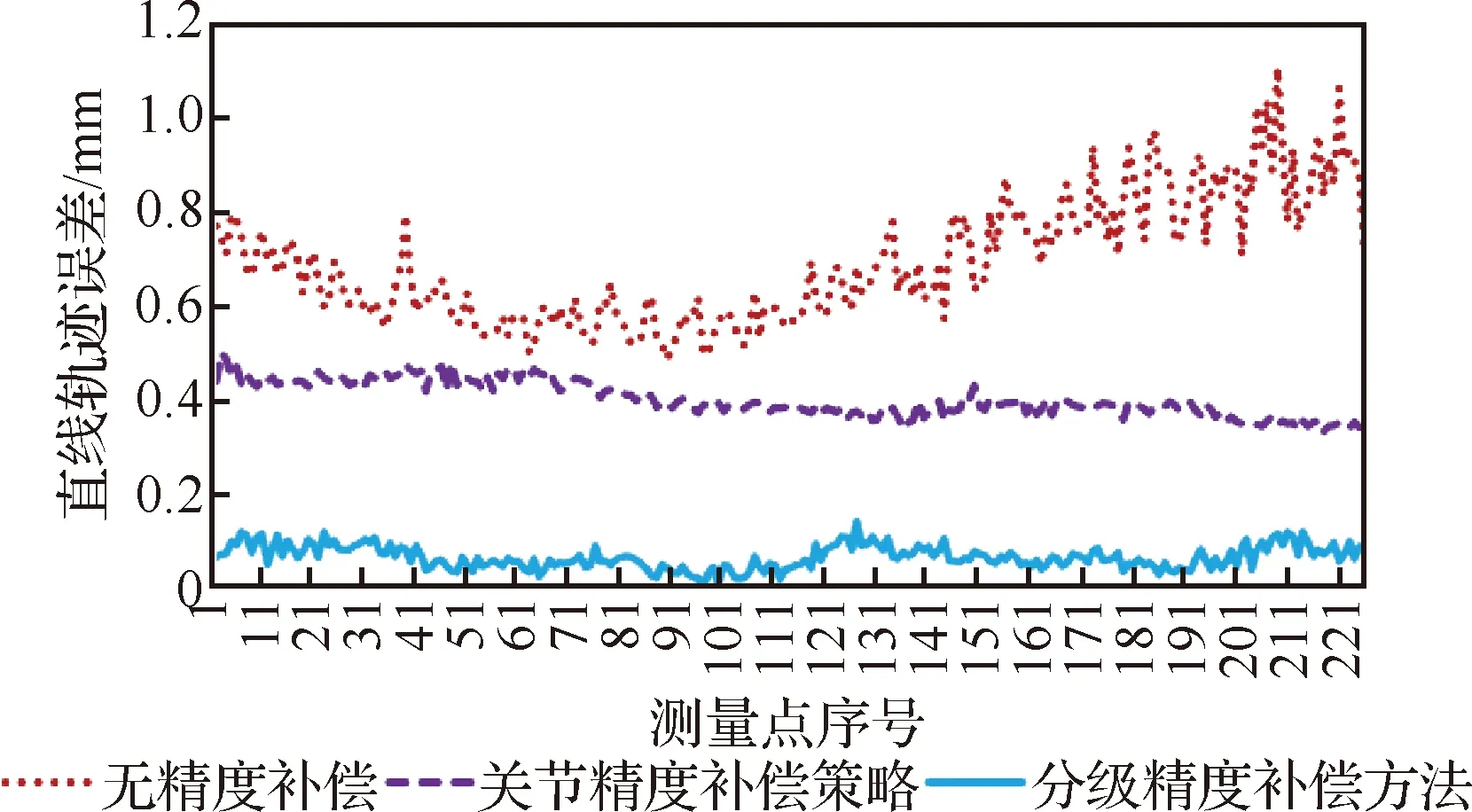
图10 机器人静载直线轨迹误差Fig.10 Robot static load linear trajectory errors

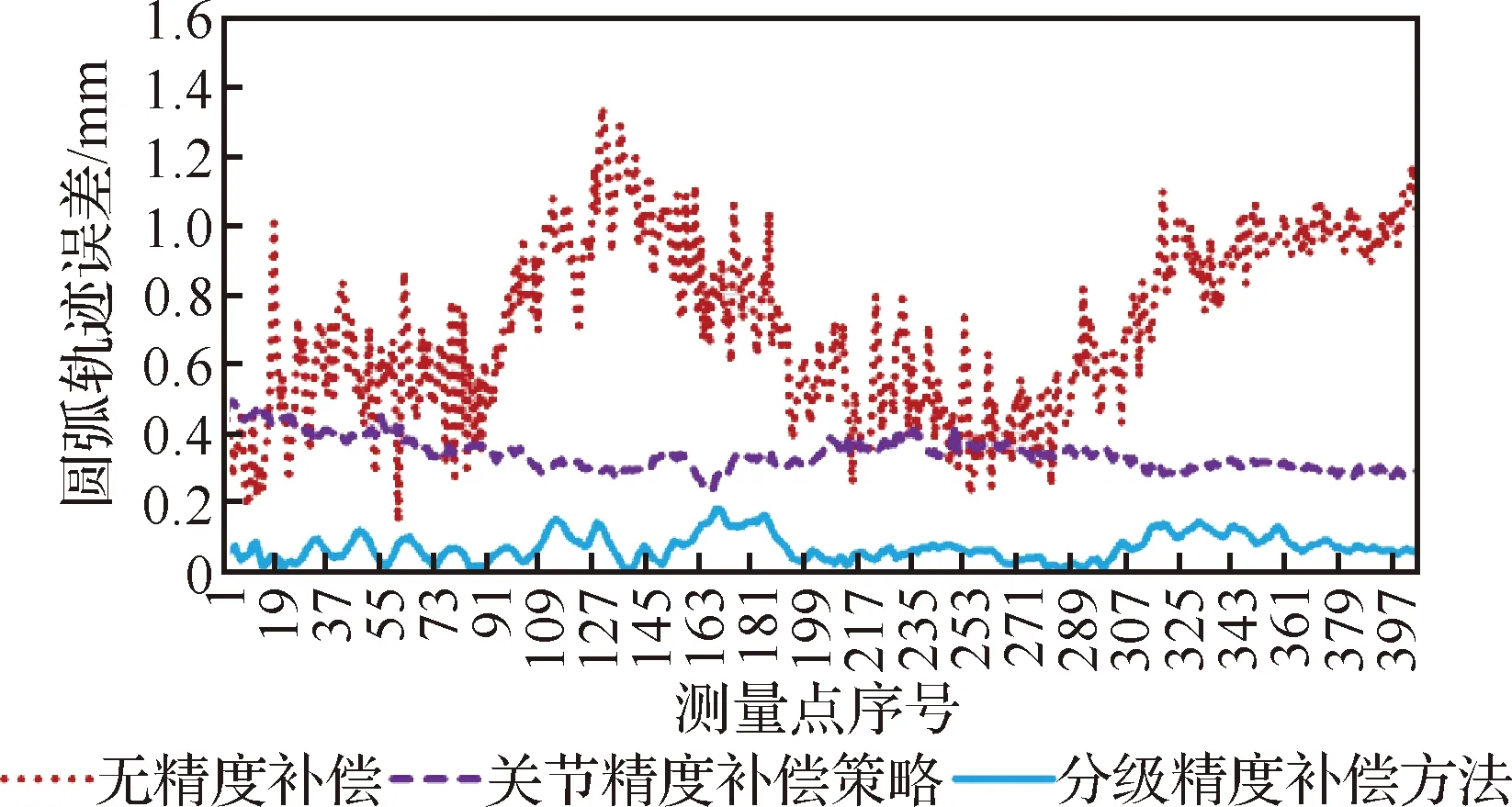
图11 机器人静载圆轨迹误差Fig.11 Robot static load circle trajectory errors

测量结果表明，关节精度补偿策略与分级精度补偿方法均对机器人轨迹精度提升明显，证明了补偿方法可以实现实时补偿。最终机器人直线轨迹精度的平均值与最大值分别提升89.93%和86.82%，圆周轨迹精度的平均值与最大值分别提升90.3%和86.55%。同时，测量结果基本符合3准则，说明轨迹的补偿试验真实反映了机器人在静载下的性能。

3 机器人铣削试验

为了验证机器人铣削系统在实际加工作业任务中的性能，在某型航天器复合材料舱段上进行了铣边试验。舱段模型与待加工特征如图12所示。

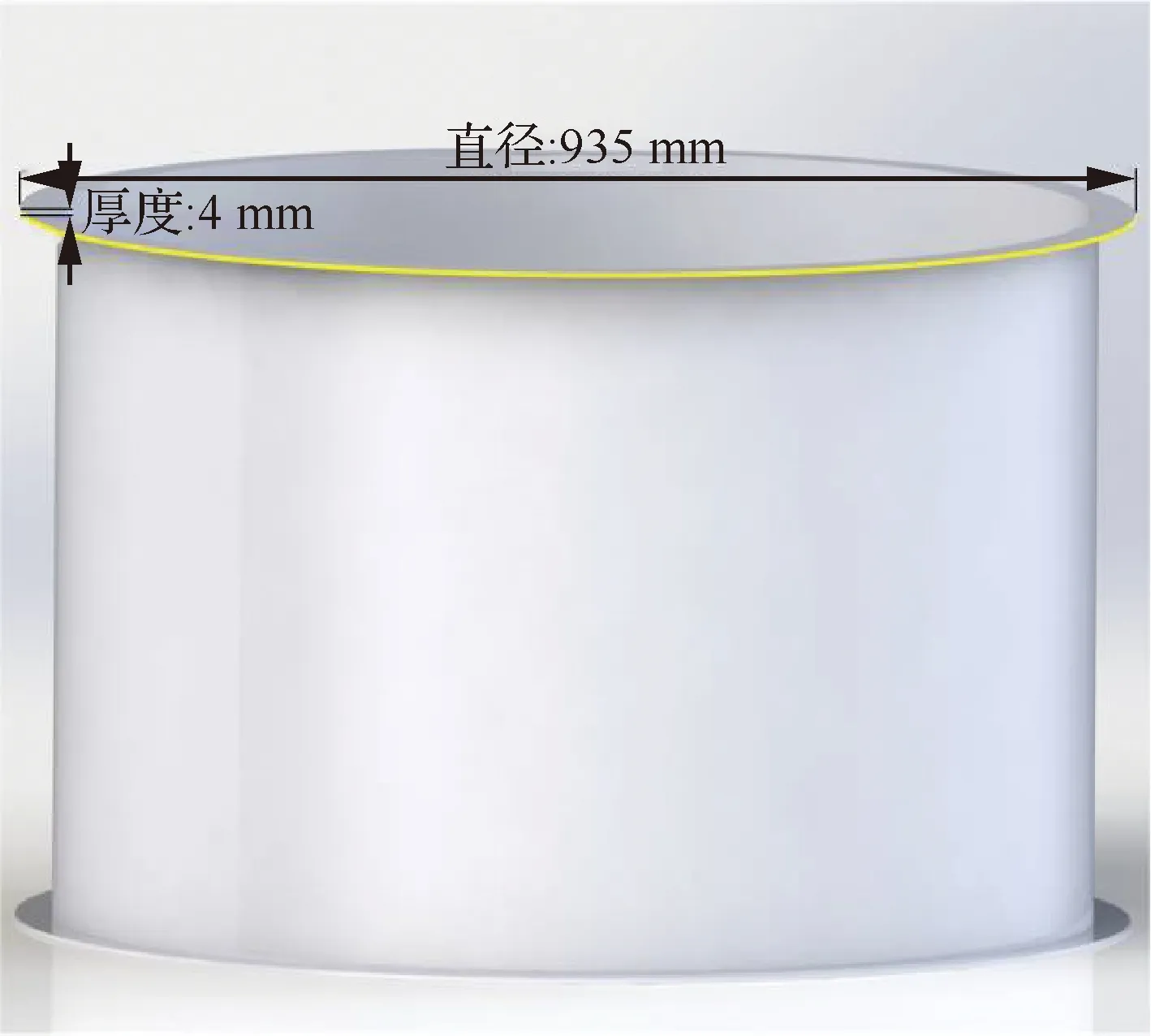
图12 舱段模型与待加工特征Fig.12 Compartment model and features to be processed

舱段下表面法兰的开槽固定在铸铁试验台上，通过激光跟踪仪对筒身和上表面进行拟合从而确定上表面法向与圆心位置。由于加工过程的粉尘会导致激光跟踪仪丢光，并且在铣削负方向半圆时会触发机器人2轴负限位报警。因此，试验中对上表面法兰侧面进行了正方向半圆弧的铣削，并对空载的轨迹和加工后的铣削面的精度以及表面粗糙度进行了测量，以此反映机器人的加工精度。但是，在测量零件圆度过程中，由于零件尺寸较大，激光跟踪仪的靶标球受零件自身干涉挡光，导致零件的部分切削区域无法测量，同时，零件尺寸大于实验室三坐标测量仪所能测量的最大范围，所以对零件加工后圆度的测量范围为121.272 5°，为机器人空载测量范围的67.37%。

铣削的刀具为直径8 mm 聚晶金刚石(PCD)铣刀，主轴转速为4 500 r/min，进给速度100 mm/min，铣削总长度1 468.69 mm，空载轨迹以及加工后工件表面的精度如图13所示。

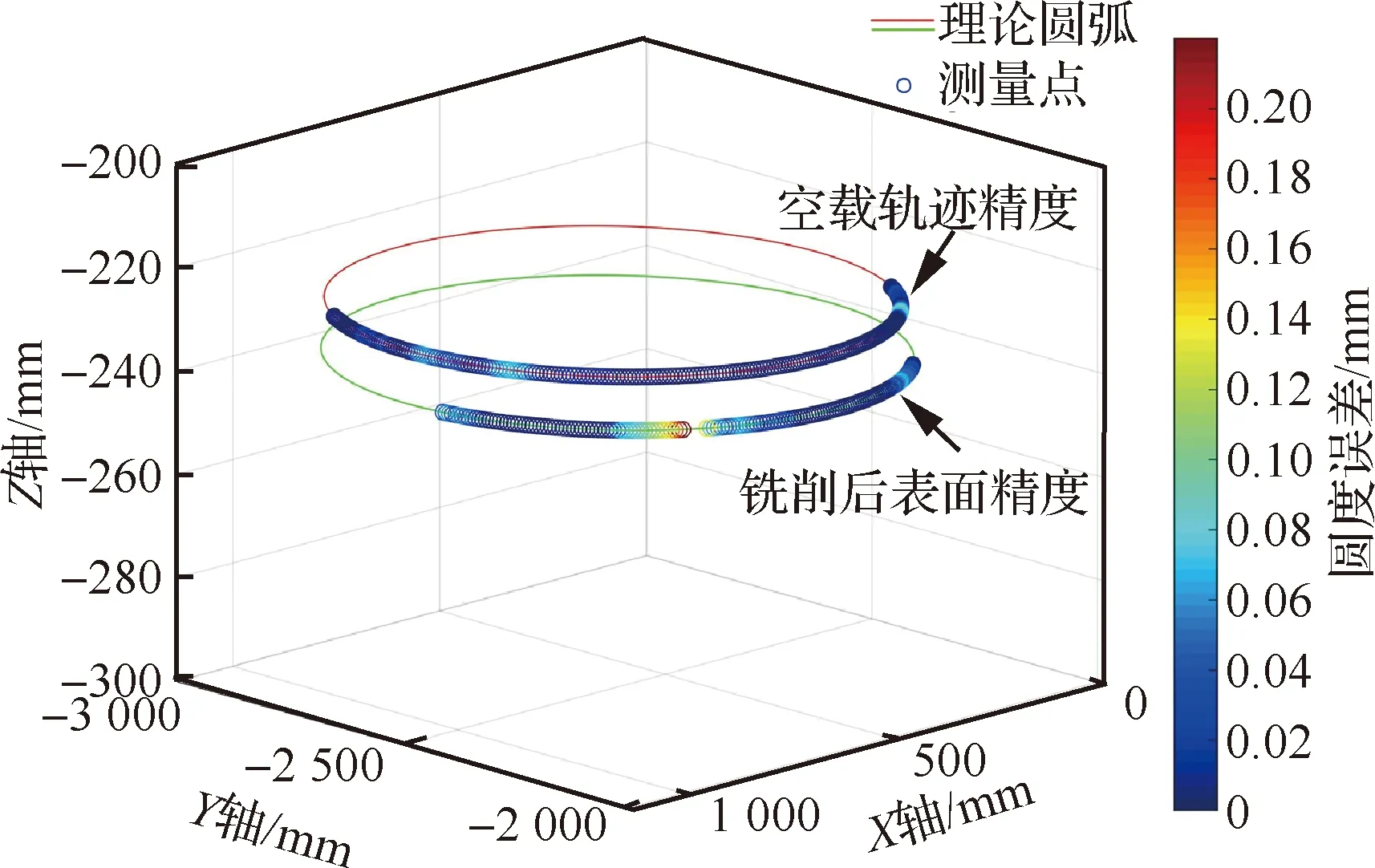
图13 空载轨迹及加工后工件表面精度Fig.13 No-load trajectory and workpiece surface accuracy after machining

测试结果表明，当机器人以100 mm/min的运行速度做圆周运动时，最大误差为0.1 mm，铣削加工误差最大0.22 mm，最大误差出现在上表面法兰宽35 mm的开槽处，如图14所示。在机器人铣削到开槽处时，零件刚性较差，加工振动明显，导致铣削误差增大。粗糙度的测量采用三丰(Mitutoyo)SJ-210粗糙度测量仪在图14标记位置共采样20个点，最终的粗糙度平均值为Ra3.75，最大值为Ra4.8。外形精度与粗糙度测量结果均满足舱段的加工要求。