基于DE-MADDPG的多无人机协同追捕策略
2022-07-04符小卫王辉徐哲
符小卫,王辉,徐哲
西北工业大学 电子信息学院,西安 710129
未来空战对抗的主要模式之一是无人机集群体系对抗,集群中的多无人机如何通过协同决策对单一逃逸无人机进行协作追捕,力求在最短的时间内捕获逃逸无人机,对于增强多无人机协同空战对抗能力具有关键作用,因此无人机集群空战对抗中多无人机追捕对抗问题研究具有非常重要的实践意义。
文献[2-7]分别研究了多机器人追逃对抗中追捕策略与逃逸策略的机动建模,包括基于微分对策、最优控制等方法的求解模型和基于双方对抗条件和运动机制分析的追捕任务和逃逸任务成功必要条件、不同速度约束下的双方机动策略、连续系统模型和棋盘环境栅格离散模型下的机动决策。但是目前围捕问题场景中大多都是设定追捕无人机速度优于逃逸无人机,而针对追捕无人机速度相对于逃逸无人机处于劣势的场景还是研究比较少。需要研究更为复杂和精确的模型,能够基于集群智能的优势,处理这种非同等运动参数条件下的追捕问题,即就是追捕无人机的速度相比逃逸无人机处于劣势时,如何通过多无人机数量的优势和相互有效合作完成对高速目标的追捕任务。
在传统的方法中,基于数学模型的方法设计的无人机控制策略,对敌方运动往往作了假定约束或者需要知道对方的控制策略,但是在战场环境下己方很难获知敌方的控制策略,同时基于数学模型设置的控制器参数往往是人工设定或者需要借助其他算法进行优化,一旦环境模型发生改变,原来旧的控制器参数可能就不是最优的,具有一定的局限性。基于无模型的强化学习则可以让无人机在环境中自主学习控制策略,而不用完全获取敌方的控制策略。
多无人机协同智能追捕可以验证多无人机的学习策略能力优劣。多智能体强化学习(Multi Agent Reinforcement Learning, MARL)结合了对策论和马尔可夫决策过程,研究随机框架下的对抗、合作和非完全合作系统中的学习,提供了一种可行的多无人机协同追捕对抗机动决策求解模型和方法。本文基于多智能体强化学习方法针对现有研究存在的问题设计多无人机的协同追捕策略。
本文研究作战空域存在4个追捕无人机与一个逃逸无人机,逃逸无人机的速度上限和追捕无人机不同,追捕无人机与逃逸者的移动范围不可超出作战空域(为了简化问题研究难度,设定对战空域),基于解耦多智能体深度确定性策略梯度算法DE-MADDPG设计了多无人机的协同追捕对抗策略。
1 问题描述与建模
1.1 多无人机追逃对抗问题
多对一追捕对抗场景中,不仅双方无人机之间要对抗,而且多无人机之间需要任务协同,场景更加复杂、对抗性更强。多无人机的追捕对抗场景研究作战空域内无人机多对一空战的情况,对抗场景可以描述如下:作战空域内存在多个追捕无人机和逃逸无人机,两方无人机具有相反的战术目的,追捕无人机要追击捕获逃逸无人机,而逃逸无人机要躲避远离追捕无人机。多无人机的追逃对抗场景如图1所示。
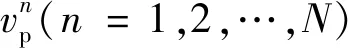

图1 多无人机追捕对抗场景Fig.1 Pursuit-evasion game of multi pursuit-UAVs and single evasion-UAV
考虑二维平面区域的追逃博弈,构造笛卡尔直角坐标系,表示追捕无人机和逃逸无人机运动状态,数学几何模型如图2所示。

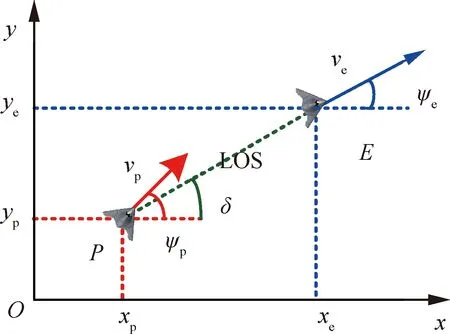
图2 二维平面追逃博弈几何模型Fig.2 Geometric model of two-dimensional plane pursuit-evasion game
追捕无人机的目标是以最短的时间捕获目标,逃逸无人机的目标是远离追捕无人机,避免在预设的作战时间段被捕获或者最大化延迟被追捕无人机捕获的时间,追逃博弈标准微分博弈数学描述为。
追捕无人机的最优化控制目标为
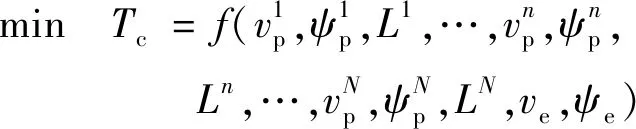
(1)
逃逸无人机的最优化控制目标为
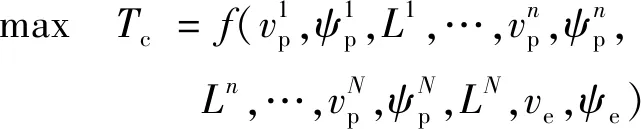
(2)
式中:(=1,2,…,)为追捕无人机到逃逸无人机的距离;为追捕无人机捕获逃逸无人机的时刻。
1.2 无人机运动学模型
无人机的运动学方程为
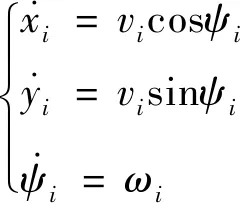
(3)
式中:=p,e;为追捕无人机或逃逸无人机的角速度的大小;为追捕无人机或逃逸无人机的速度大小,是一个固定的值,即在飞行过程中不改变。
无人机的运动控制变量约束为

(4)
式中:、分别为追捕无人机和逃逸无人机的最大角速度,其计算方程为
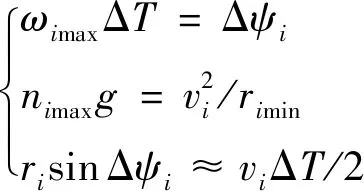
(5)
式中:=p,e;Δ为仿真的时间步长;为转弯半径;min为最小转弯半径;Δ为Δ时间内的航向角最大转弯角;max为无人机的最大侧向过载。因此,由式(5)可得最大角速度的确定公式为
max=arcsin(Δmax(2))Δ
(6)
捕获条件为式(7),即敌我距离在追捕无人机的捕获半径范围内,捕获半径可以是无人机的载荷作用范围或者武器攻击范围。

(7)
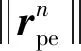
由于本文假定追捕问题是在有限的二维平面内进行的,因此无人机在设定的环境边界内运动需要满足式(8):

(8)
式中:=1,2,3,4;、分别为环境边界的最小横坐标和最大横坐标;、分别为环境边界的最小纵坐标和最大纵坐标。
在研究中,定义速度比为追捕无人机的最大速度和逃逸无人机最大速度之比:
=
(9)
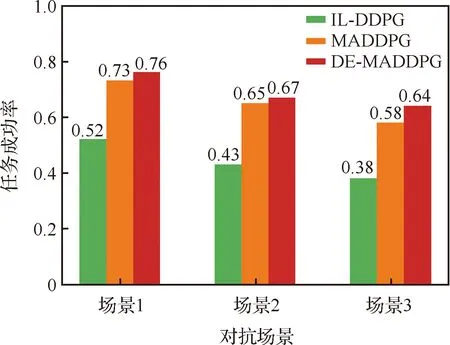
双方无人机各占优势,追捕无人机数量多于逃逸无人机,逃逸无人机的最大速度大于追捕无人机。文献[3]基于阿波罗奥尼斯圆(Apollonius Circle)和几何规律研究了多追捕者-单逃跑者追逃问题实现成功捕获的约束条件,即速度比 ∈[sin(π),1) (10) 多智能体强化学习是多无人机协同控制优化的一种求解模型框架,每个环境实体的策略输出都有各自的神经网络控制。它是一种多智能体系统研究领域的分布式计算技术,结合了强化学习技术与博弈论技术,可以使多个智能体在高维、动态的真实环境下通过通信交互和协同决策完成错综复杂的任务,具有自主性、分布性、协调性的特点,具备学习能力、推理能力、自组织能力,是分布式人工智能的演变。 多智能体强化学习算法是以马尔可夫决策过程为基础的随机博弈框架,可以表示为式(11)的高维度元组。 (11) 式中:为马尔可夫决策过程模型的状态集;为智能体的数量;=××…×,为所有智能体联合动作集;为每个智能体的奖励回报,××→;状态转移函数:××→[0,1];为累计折扣奖励的衰减系数。 多智能体系统中,状态转移是所有智能体共同执行行动的结果,获得的奖励取决于联合策略,联合策略:(|)=∏∈(|)为所有智能体的联合决策策略和,×→,每个智能体的奖励为 (12) 状态值函数和状态-动作值函数在多智能体下的贝尔曼方程如式(13)和式(14)所示: (13) =] (14) 一般来说,根据多智能体强化学习要完成的任务类型,可分为完全合作、完全竞争和混合类型,本文的多追捕无人机协同决策属于完全合作类型。完全合作类型各智能体的目标就是最大化共同回报,所有智能体的奖励函数都是相同的。其他类型情况下,奖励函数通常不同且相关,独立最大化的难度比较大。因此完全合作类型智能体的奖励函数,很适合做MARL的目标,此时学习目标可以表述为 +1(,)=(,)+[+1+ (15) 式中:为学习率参数。 MADDPG是DDPG(Deep Deterministic Policy Gradient)在MARL的扩展,各智能体都采用DDPG框架,各智能体策略参数为=(,,…,),联合策略为:=((),(),…,())。它的核心思想是通过集中训练、分布执行的框架来寻找最优联合策略,可以解决MARL环境的非平稳性及经验回放(Experience Replay, ER)方法失效的问题。MADDPG能解决环境不稳定性的原因在于如果已知所有智能体策略,即使智能体的策略发生变化了,环境的稳定性不受影响。多智能体系统动力学模型为 (′|,,,…,,,,…,)=(′|, ,,…,)=(′|,,,…,,′, ′,…,′) (16) 因为≠′时,式(16)仍然成立,所以环境仍然是稳定的。 MADDPG的经验池设计为 (17) 所谓“集中训练,分散执行”,指的是中心化训练、去中心化执行,即通过训练学习得到的最优策略,应用的时候仅需要利用智能体的观测信息-局部信息就能输出最优动作。集中训练时,在基础DDPG算法上叠加一些额外的信息得到更准确的Q值计算,反馈Actor网络,这些值可以是其他智能体的状态、动作,每个智能体不仅根据自己的观测值、动作,还根据其他智能体的动作来评估当前Actor输出动作的价值。值计算为 =(,,,…,,) (18) 式中:为Critic网络的网络参数。 每个智能体的Critic网络输入相同,损失函数计算为 (19) 相当于建立了一个中心化的Critic网络,并给出对应的值函数,也一定程度缓解环境不稳定的问题。但是Actor仅需要局部信息,实现了分布式控制。 Actor网络的参数更新为 (20) 分散执行指训练完成后,每个Actor可以根据自己的观测值采取合适动作,不需要其他智能体的动作。MADDPG算法中的Actor网络和Critic网络协同配合如图3所示,每个智能体使用独自的Actor,输出确定的动作,但是Critic网络输入除过自身的观测状态信息、动作信息外,还包括其他智能体的动作信息。每个智能体对应一个中心化Critic网络,该网络同时接受所有智能体Actor网络产生的数据。 图3 MADDPG的中心化训练和去中心化执行Fig.3 Centralized training and decentralized execution of MADDPG 基础的MADDPG算法框架图如图4所示。训练过程中,每个智能体依靠自身策略得到当前时刻状态对应的动作,然后执行动作与环境进行交互,获得经验后存入公众经验池。当所有智能体都和环境进行交互后,每个智能体从公众经验池中随机抽取批数据训练神经网络。MADDPG通过全局的值更新局部的策略,但是需要全局的状态信息和所有智能体的动作信息。OpenAI将MADDPG算法放在游戏场景中进行验证,游戏决策中状态和动作是离散的,实际的问题一般状态和动作是连续的,本文研究将MADDPG应用于较为接近真实的多无人机追逃对抗场景中,所用环境模型充分考虑了无人机的动力学特性和物理特性,相比较理想的游戏环境更为复杂。 图4 MADPPG基本框架示意图Fig.4 Basic framework of MADDPG DE-MADDPG算法是一种MADDPG的改进算法,能够同时以解耦的方式最大化全局奖励和局部奖励,而不用在每个智能体的奖励设计中考虑全局奖励和局部奖励。从MADDPG算法的介绍可以看出,MADDPG是通过全局的中心化Critic网络实现集中训练,DE-MADDPG算法则改进了网络架构,除了一个全局的Critic网络,还同时为每个智能体构建了一个局部的Critic网络,如图5所示。全局Critic网络的作用是最大化全局奖励,局部Critic网络的作用是最大化局部奖励。 图5 DE-MADDPG的中心化训练和去中心化执行[21]Fig.5 Centralized training and decentralized execution of DE-MADDPG[21] DE-MADDPG算法的创新之处在于结合了MADDPG算法和DDPG算法,同时也是一个“集中训练,分散执行”的架构,仅在训练阶段需要额外的其他智能体状态和动作信息,应用执行时只需要智能体自身的状态就可以输出策略动作。MADDPG算法中,智能体的策略梯度为 )|=()] (21) DE-MADDPG引进了局部的critic网络,智能体的策略梯度计算会变为 (22) (23) 式中:的定义为 (24) 式中:′={′,′,…,′}为网络参数′={′,′,…,′}定义的目标策略。 (25) 式中:的定义为 (26) 多无人机协同追捕问题是控制每个无人机协同去完成同一个任务,所以存在无人机的整体目标与个体目标,很适合用DE-MADDPG算法来进行多无人机的协同追捕策略训练。本文从多无人机的具体追捕任务出发,设置了解耦型奖励回报函数,然后基于DE-MADDPG算法对多无人机进行了训练。 奖励函数设计采用引导性奖励和稀疏奖励相结合的方式,主要考虑无人机的协同要求和目标任务要求,具体来说就是2个要求,一是各无人机之间要考虑避碰,即无人机之间不能互相碰撞,二是要协同以最快时间追捕逃逸无人机。多追捕无人机的任务目标,是追求任一架追捕无人机成功捕获逃逸无人机,因此奖励函数的设计中,主要考虑距离因素。 解耦性奖励函数需要设计全局奖励函数和局部奖励函数。对于多追捕无人机的协同追捕对抗策略训练,全局奖励考虑多无人机的任务目标,即追求最快让多无人机中某一架无人机完成追捕捕获任务;局部奖励中完成对每个无人机的避碰控制和任务目标控制。这样的全局奖励函数和局部奖励函数相结合的方式,会很快引导无人机的决策网络更新到较优参数。 3.1.1 全局奖励函数设计 追捕无人机的整体奖励设计为 =- (27) 式中:和为控制奖励幅度的系数;为与逃逸无人机位置(,)距离最近的追捕无人机到逃逸无人机的距离;的确定方式为 (28) 3.1.2 局部奖励函数设计 无人机的局部奖励函数设计,分为以下3个模块。 1) 定义无人机互相碰撞的惩罚回报奖励为 c= (29) 式中:为无人机之间的最近安全距离;为第架追捕无人机与第架追捕无人机之间的距离。 2) 当追捕无人机编队成功捕获逃逸无人机时,给予正奖励回报。 (30) 式中:(=1,2,…,)为追捕无人机到逃逸无人机的距离;为奖赏值。 3) 定义任务引导奖励为 p=- (31) 所以,每个无人机的奖励为上述3个奖励函数的加权和: =p+c+f (32) 式中:、、为加权系数,并且满足++=1。 基于DE-MADDPG的多无人机协同追捕对抗策略训练算法流程如算法1所示。 算法1 基于DE-MADDPG的多追捕无人机协同追捕策略训练算法Algorithm 1 Multi-UAVs cooperative pursuit strategy using DE-MADDPG 为了方便算法的实现和使用,这里将训练算法中间用到的超参数及其物理意义做下介绍,训练算法参数表如表1所示。 表1 训练算法参数Table 1 Training algorithm parameter 实验采用图1场景想定,同时采用常见的红蓝对抗作战法,设定红方为追捕无人机,蓝方为逃逸无人机。仿真环境全部基于Python语言编写,利用Pycharm Community 2020.2和Anaconda3平台,深度学习环境采用Tensorflow 1.14.0,计算机配置为CPU Inter i7-9700F@3.00 GHz,内存16 GB。 无人机通过观察环境状态,根据设定的控制策略得到控制量,再利用环境的反馈调整控制策略,形成一个闭环训练过程。实验设定的训练参数表如表2所示。 表2 训练超参Table 2 Training hyperparameters 对多追捕无人机单逃逸无人机追逃对抗仿真实验设置作以下说明: 1) 所有的追捕无人机为同构无人机,即追捕无人机的性能参数完全相同,并且追捕无人机之间采用全连通通信网络。 2) 为了增加研究的难度,设定追捕无人机和逃逸无人机的运动性能不同,即研究多低速追捕无人机和高速逃逸无人机的追逃对抗。 3) 这种场景下追逃博弈的结果与初始时追捕无人机的初始阵位、逃逸无人机的位置紧密相关,同时考虑深度强化学习算法的应用特点,设置多无人机协同追逃对抗实验处在二维有限的正方形区域内,即[-700,700] m×[-700,700] m,该环境包括4个追捕无人机和1个逃逸无人机。 4) 为了进行有效的高速训练,设定逃逸无人机的初始位置为原点(0,0),4个追捕无人机的位置分别位于[-200,200] m×[-200,200] m的4个象限,如图6所示,其中红色的是追捕无人机,蓝色的是逃逸无人机。 图6 多追捕无人机单逃逸无人机追逃对抗初始状态Fig.6 Initial state of pursuit-evasion game with multi pursuit-UAVs and single evasion-UAV 5) 实验中环境参数设置如表3所示。 表3 多无人机追逃对抗环境实验参数Table 3 Initial parameters of simulation experiment of multi-UAVs pursuit-evasion game 为了验证DE-MADDPG的训练效果,将DE-MADDPG算法同MADDPG算法、IL-DDPG(Independent Learning-DDPG, IL-DDPG)算法进行对比,同时应用3种算法于多追捕无人机的协同追捕对抗策略,观察对比3种算法的训练效果。其中,IL-DDPG指各追捕无人机的训练学习和控制过程都用独自的DDPG网络,每个无人机仅能获得自己的信息和逃逸无人机的信息,拥有一套Actor网络和Critic网络,使用基本的DDPG网络训练。MADDPG算法的网络结构如图7(a)所示,DE-MADDPG算法的网络结构如图7(b) 所示。 图7 MADDPG和DE-MADDPG网络结构Fig.7 Network architecture of MADDPG and DE-MADDPG 训练时逃逸无人机的运动控制策略根据具体对抗场景而定。设定敌机运动控制策略为随机运动策略控制方式时,4架无人机在3种算法下的平均奖励曲线如图8所示。 图8 无人机的平均奖励曲线Fig.8 Average reward curves of UAVs 根据实验数据观测,所有无人机的平均奖励都取得收敛效果,训练之初无人机的总奖励比较小且是负奖励,这说明训练之初无人机采取的策略是不合法的,随后的训练学习中无人机逐渐学到了提高总奖励的策略。对比DE-MADDPG、MADDPG、IL-DDPG算法的训练效果,可以得到2个结论,一个是基于多智能体强化学习(DE-MADDPG、MADDPG)算法相比单智能体强化学习(IL-DDPG)算法取得了更好的收敛效果;另外一个是DE-MADDPG算法相比MADDPG算法取得了更快的收敛效果,从训练曲线证明了DE-MADDPG算法的优势。另外一方面,部分无人机的DE-MADDPG算法收敛稳定性比MA-DDPG算法差,这是由于DE-MADDPG算法同时要兼顾整体目标与个体目标,而MADDPG算法只考虑个体目标,导致的DE-MADDPG算法收敛稳定性相对较差。 为了验证基于DE-MADDPG算法的追捕无人机协同追捕策略的优劣,设置3种对抗场景来验证设计的协同追捕策略训练算法。 多追捕无人机围捕随机运动逃逸无人机 设置逃逸无人机采用随机运动策略控制方式。对应的仿真实验结果如图9所示。 图9 场景1:DE-MADDPG vs随机运动策略Fig.9 Scene 1: DE-MADDPG vs random strategy 场景1仿真结果表明,这是一个典型的成功实验样本,逃逸无人机并不具备对抗策略,只是随机选择运动方向,逃逸无人机在14.78 s时被4号追捕无人机所抓捕,由于采用随机运动策略的逃逸无人机具有随机机动性并且不可预测,所以花费的时间还是相对较多。通过第一种场景的训练测试表明了所设计算法的有效性。 多追捕无人机围捕灵活逃逸策略的逃逸无人机 逃逸无人机采用如下的灵活逃逸对抗策略,即将对战态势综合简单考虑,当被追捕无人机包围的时候,逃逸无人机向着追捕无人机构成的多边形所有边长中点中最远距离的中点逃逸,如图10(a)所示方向,为、、、中距离最远的点;当没被逃逸无人机包围时,采取人工势场法的思想,向所有追捕无人机给予的斥力矢量综合后的斥力方向逃逸,即图10(b) 所示,其中综合斥力矢量的方向计算如式(33)所示 图10 逃逸策略示意图Fig.10 Schematic of escape strategy 方向,为斥力、、和的矢量合力方向。 (33) 图11 场景2:DE-MADDPG vs灵活逃逸策略Fig.11 Scene2: DE-MADDPG vs flexible escape strategy 场景2仿真结果表明,逃逸无人机采用图10中的逃逸方向进行逃跑,先机动变化航向至3号和4号追捕无人机的中心,但面临围堵后进行快速机动,再快速逃逸,最后在21.66 s被1号无人机抓捕。通过第2种场景的训练测试表明了所设计算法的有效性。 多追捕无人机围捕转义策略的逃逸无人机设置逃逸无人机采用训练出来的逃逸策略,也称为转义逃逸策略,逃逸策略的训练算法参考文献[27]。对应的仿真实验结果如图12所示。 图12 场景3:DE-MADDPG vs转义逃逸策略Fig.12 Scene 3: DE-MADDPG vs learned strategy 场景3仿真结果表明,训练出来的转义策略通过初始的状态和条件判断,右上方应该为自己的首先逃逸方向,但是追捕无人机也通过自己的态势感知快速地进行围堵,队形收缩,在逃逸无人机连续逃脱3号、4号、1号无人机的围堵后,1号无人机和2号无人机的相互协作,成功在29.10 s围堵抓捕逃逸无人机。通过场景3的训练测试表明了所设计算法的有效性。 从以上仿真可以得出结论,训练出来的协同追捕策略具有明显的合作行为,追捕无人机不仅简单地跟踪逃逸无人机,而且表现出一些高级的协同行为,极大地提高了追捕任务的执行效率,同时所设计训练算法对于不同逃逸策略的快速逃逸无人机也能够较好地适用。为了验证所设计训练算法得到的多无人机协同追捕策略实际使用时的稳定性和鲁棒性,将DE-MADDPG、MADDPG、IL-DDPG算法训练得到的多无人机协同追捕策略分别在3种逃逸无人机智能程度不同的场景中进行10 000次的蒙特卡洛仿真,统计最终的成功率,如图13所示(场景1、场景2、场景3)。蒙特卡洛仿真中每次追捕无人机的初始位置和初始航向、逃逸无人机的初始位置和初始航向都采用随机生成方式。 图13 多无人机协同追捕逃逸训练效果成功率Fig.13 Success rate of training result of multi-UAVs cooperative pursuit-evasion strategy 从图13可以看出,随着敌机逃逸无人机智能程度的提高,对战场景的复杂程度提高,无论是基于哪种强化学习算法,训练效果的成功率都会随之降低;DE-MADDPG训练算法相比MADDPG、ILDDPG能得到更高的追捕对抗任务成功率,IL-DDPG由于是无人机独立地进行学习,学习训练阶段没有多无人机的协同,取得的追捕任务成功率最低。对战是否成功不仅取决于训练效果的好坏,同时取决于追捕无人机和逃逸无人机的初始态势,有些态势下再好的训练效果也无法让多追捕无人机成功完成追捕任务。本文所设计的多追捕无人机协同追捕策略是针对固定数量的4架追捕无人机,如果对抗场景中有更多的追捕无人机或者速度比设定更大,则取得的任务成功率会更高。 综上所述,仿真实验验证了所提出的方法在多追捕无人机对快速的单逃逸无人机追逃对抗中的有效性和计算效率。不同于其他微分对策或者基于几何的控制律方法,不需要针对对战过程进行精确的物理建模和推导,只需要对多无人机的作战任务进行奖励函数设计,在多智能体深度强化学习框架下进行足够的训练,就可以得到接近于传统控制方法的控制效果,同时神经网络的参数可以提前训练学习,运行时直接端到端执行就可以,算法的运行时间也有所提高。本文所用DE-MADDPG算法具有广泛的使用场景,针对其他多无人机协同控制任务,稍微修改后就可以进行实际的使用。 本文围绕面向快速目标的多无人机协同追捕问题,提出了一种基于解耦型的多智能体强化学习算法,使得多无人机具有较强的协同围捕能力,主要结论如下: 1) 提出了多无人机任务学习的局部奖励函数和全局奖励函数设计方法,使得无人机将个体和总体的奖励目标得以解耦,从而让无人机向更明确的任务进行训练学习。 2) 提出了基于DE-MADDPG算法的多无人机协同追捕策略,能够通过协同决策完成对快速目标的捕获。 3) 设计逃逸无人机的多种逃逸控制策略并进行算法测试,实验结果表明本文提出基于DE-MADDPG的多无人机协同追捕策略有着不错的应用效果,相比IL-DDPG、MADDPG算法的应用效果有着更好的训练表现。 在进一步的研究工作中,可以将本文的算法拓展到三维环境的多无人机追逃博弈问题中,能够更接近真实空战状况。2 DE-MADDPG算法
2.1 多智能体强化学习算法
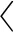
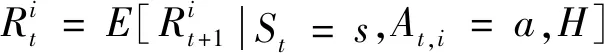
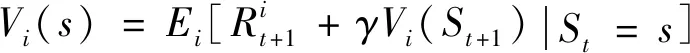
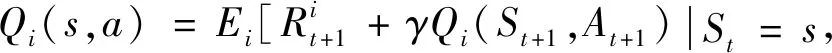
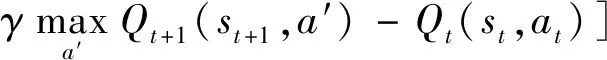
2.2 MADDPG算法
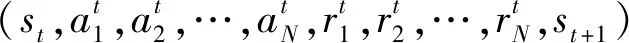
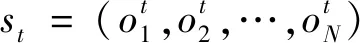


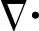
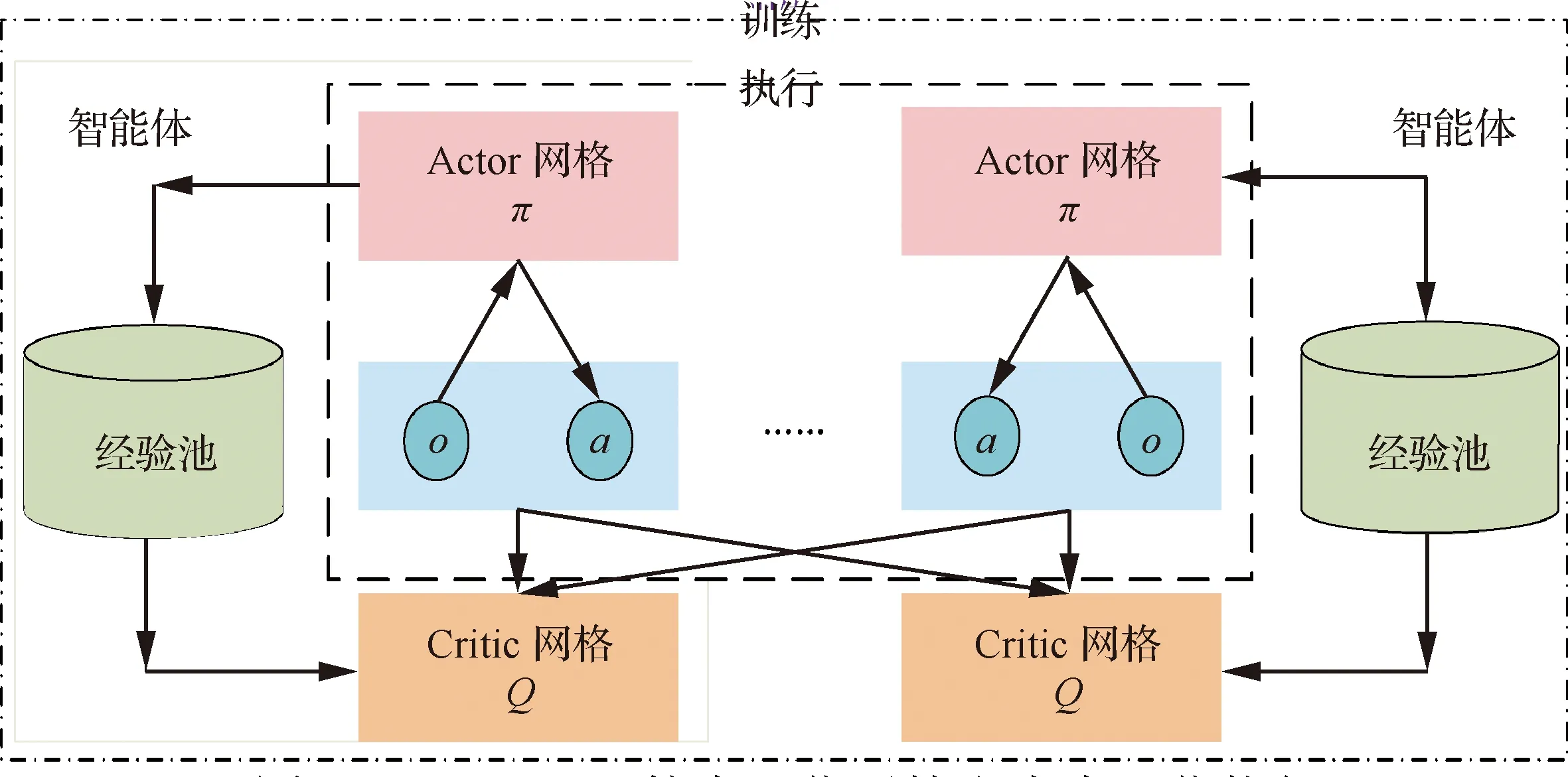

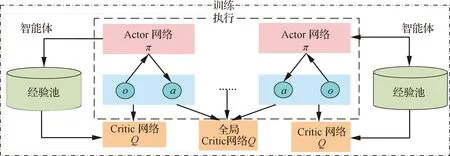
2.3 DE-MADDPG算法
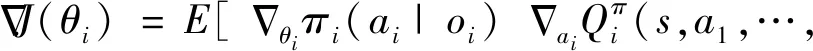


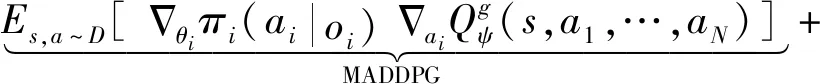

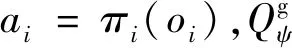
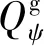


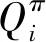


3 多无人机协同追捕策略设计

3.1 解耦型奖励回报函数设计
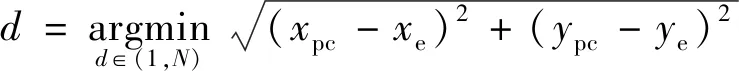


3.2 训练算法流程

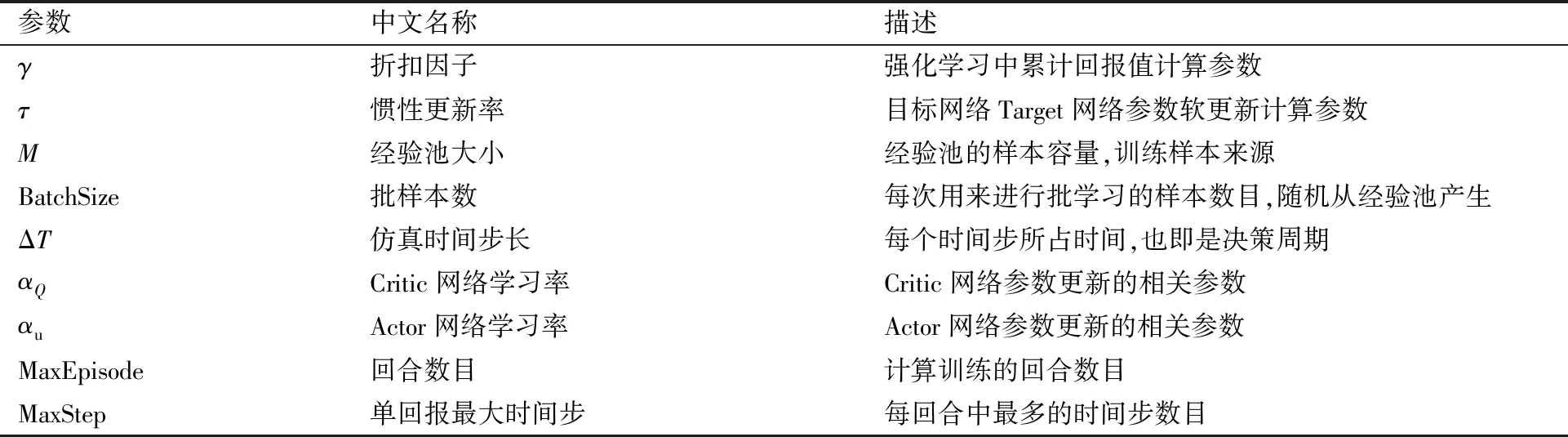
4 仿真验证
4.1 实验设置
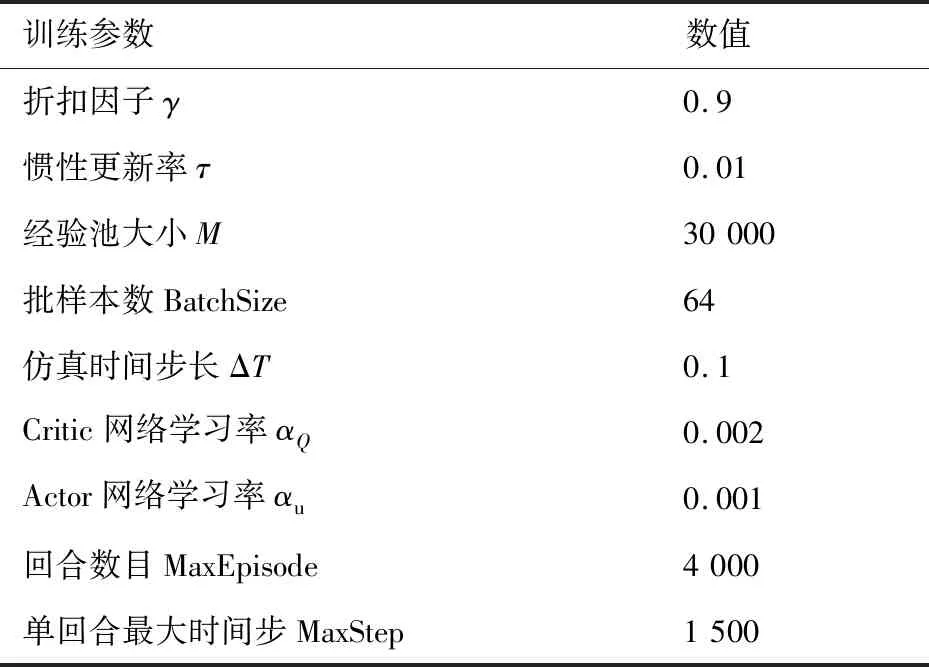
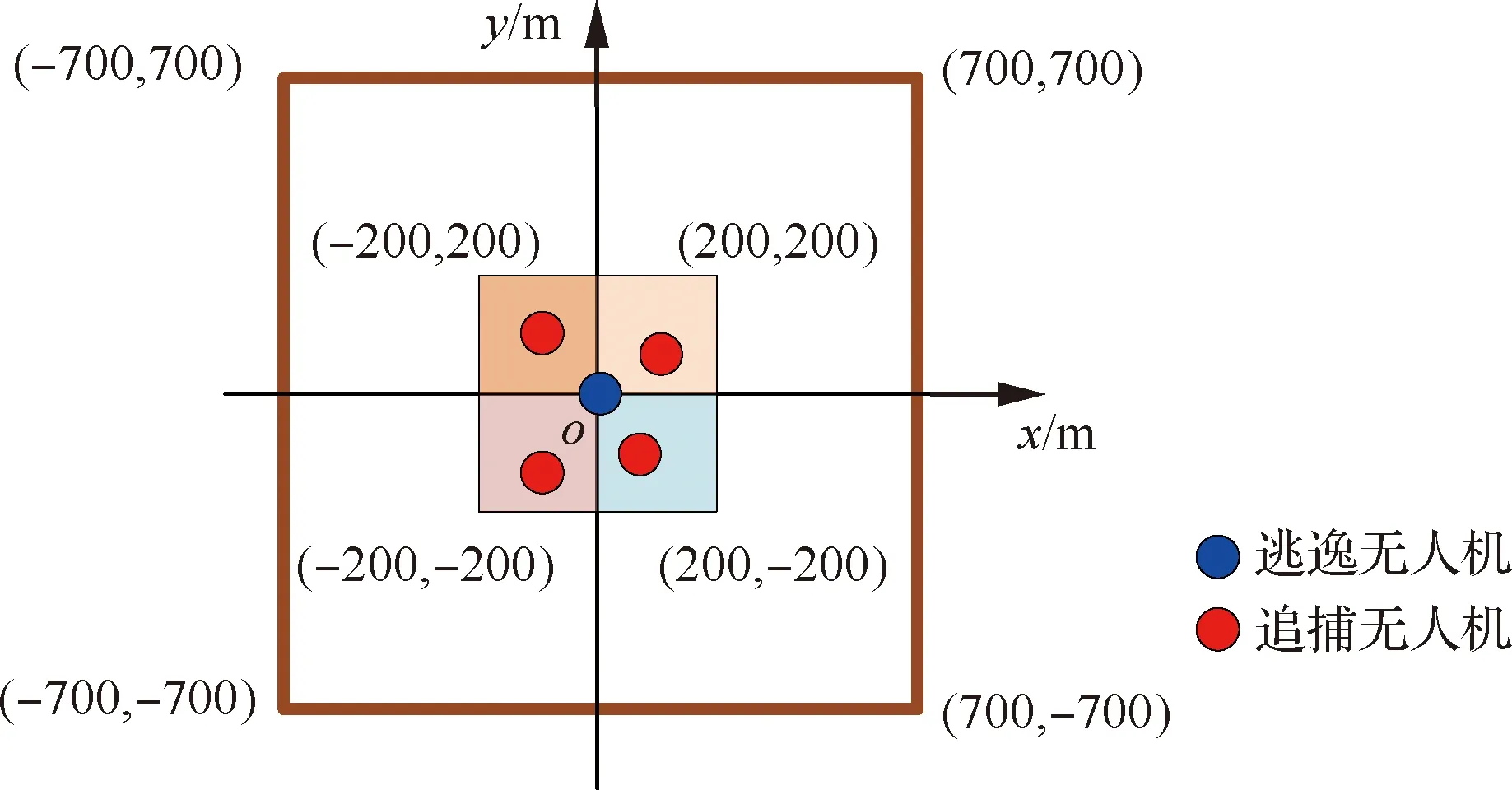

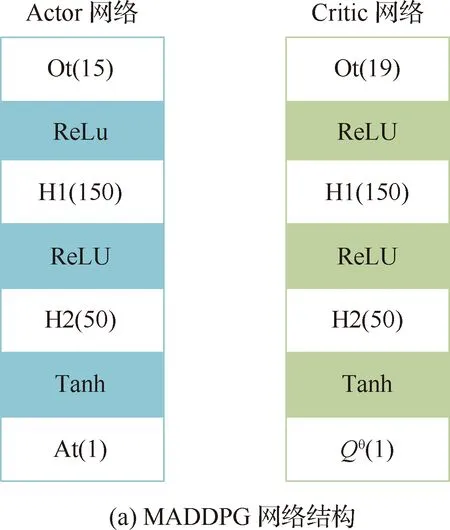
4.2 方法有效性实验
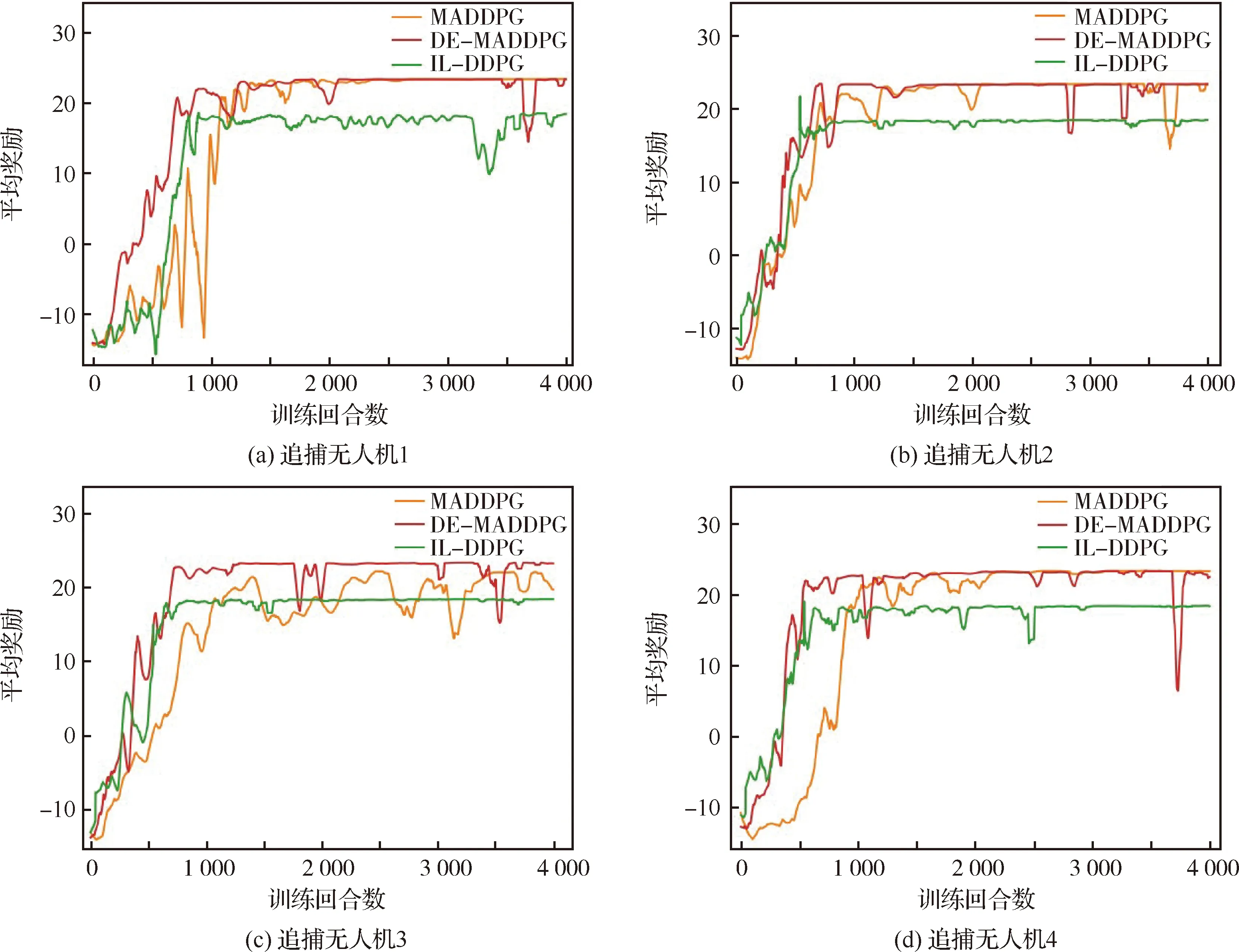
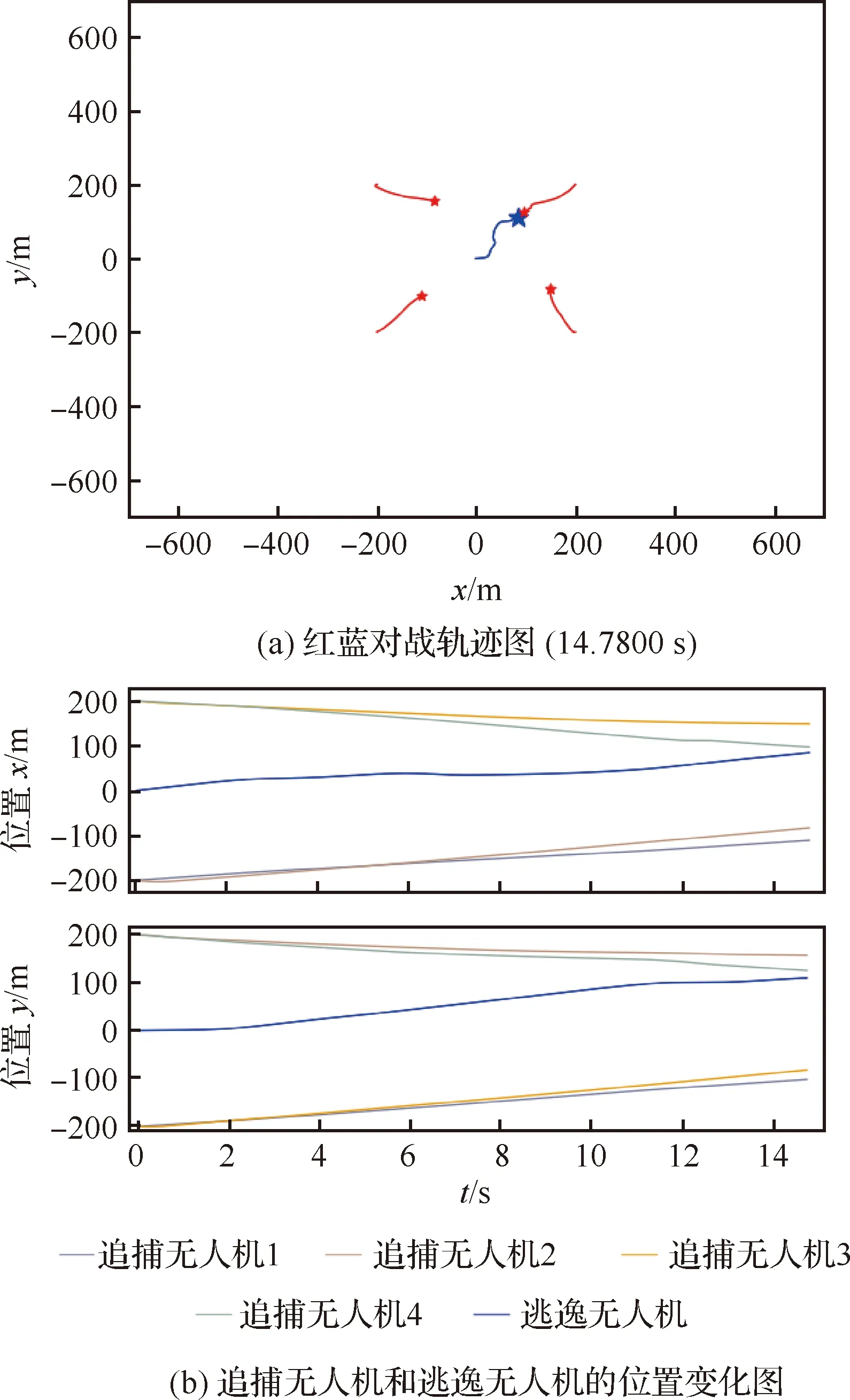
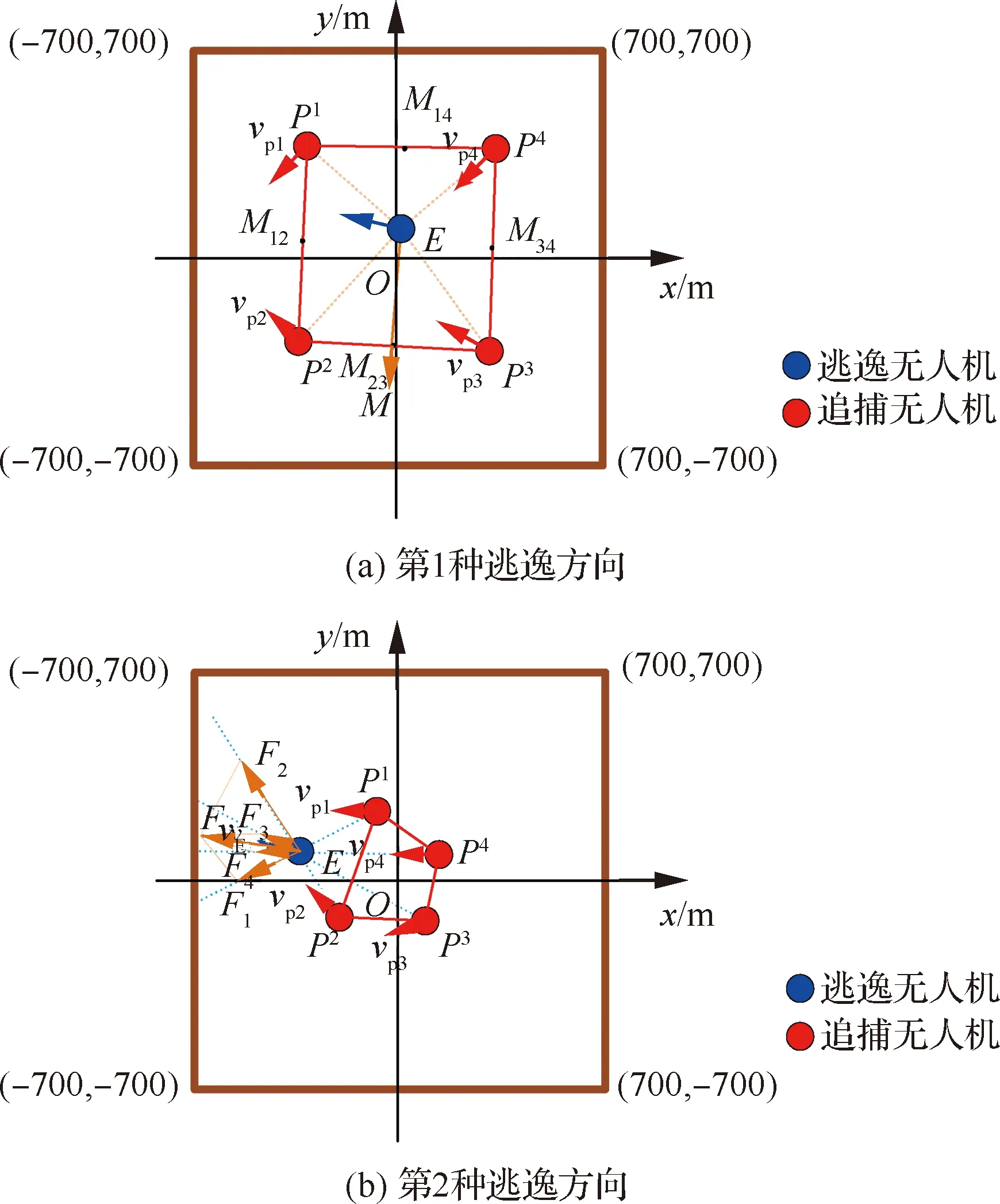

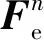
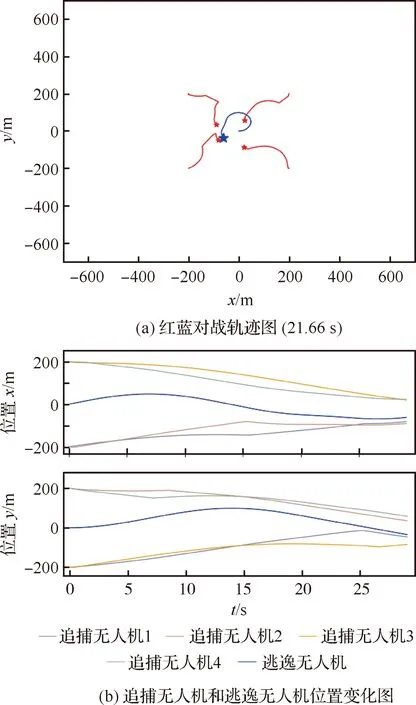

5 结 论
