复合材料整流罩减振降噪的动力吸振器设计

2022-07-04李航行胡迪科吴邵庆

航空学报 2022年5期

李航行，胡迪科，吴邵庆,3,*

1. 东南大学工程力学系，南京 211189

2. 上海宇航系统工程研究所，上海 201109

3. 东南大学江苏省空天机械装备工程研究中心，南京 211189

运载火箭发射阶段恶劣的声振环境会导致整流罩内电子设备的失效，需要开展整流罩的隔声性能设计。利用有限的附加质量来最大限度地提高隔声性能，降低整流罩内部噪声量级一直是研究者关注的重点问题。目前关于火箭整流罩内噪声抑制的手段大体可以分为几类：① 基于动力吸振的降噪方法，该方法通过减小结构振动来降低其声辐射，达到降噪目的；② 基于周期结构设计的降噪方法。弹性波在周期弹性复合介质中传播时，会产生弹性波禁带，禁带内的弹性波会激发内部散射体的共振模态，散射体的共振模态与基体的行波模态产生强烈的相互作用，使得周期结构的振动沿传播方向不断衰减。利用周期结构禁带内弹性波衰减的特性抑制禁带内结构的振动进而降低声辐射。在上述方法中，基于动力吸振器的方法由于其理论相对成熟、成本低、安装方便等优点，被广泛应用于各类工程减振降噪中。Wen等将磁流变吸振器应用在火车中，显著提高了车辆行驶平稳性；Liu和Zhu将负刚度吸振器应用在有砟轨道上，在共振频率附近较宽频段内获得较好的振动噪声抑制效果；林武斌和滕汉东将波纹管吸振器应用在输油泵上，试验显示减振效果达到55%。

虽然吸振器理论相对成熟，但适合于复杂结构减振的理论研究并不多。目前较多采用的方案为采用模态参数识别的方法，将主系统等效为单自由度系统进行优化设计，但该方法受限于识别算法的精度且针对耦合模态识别精度不高，很难应用到复杂结构上。Zhu等基于模态叠加法推导了分布式吸振器平板的解析解，从理论层面给出了吸振器最优材料参数解，但该方法仅对单模态的响应抑制进行了讨论，针对多模态耦合工况下响应的抑制没有给出结果，难以推广到复杂结构。

为了发展适用于复合材料整流罩结构减振降噪的动力吸振器设计方法，本文提出了一种基于基变换模态空间内的降维理论，用以解决考虑多模态耦合工况下动力吸振器设计，将耦合模态利用空间投影进行解耦，将维结构模态空间内的动力吸振器优化问题降维成一维空间的动力吸振器优化问题，并进一步利用单模态工况下的动力吸振器参数优化方法获取优化参数。本文的研究将仅适用于包含稀疏模态的简单结构的动力吸振器设计方法推广到包含多模态耦合的复杂结构，实现复合材料整流罩结构的减振降噪目的。

1 Nomex纸蜂窝板力学等效模型

针对由Nomex纸蜂窝夹芯板组成的整流罩结构，直接开展有限元建模会导致模型自由度过于庞大，难以实现高效的声振分析和隔声性能优化设计。因此，需要开展Nomex纸蜂窝夹芯板的力学等效建模。

图1所示整流罩用Nomex纸蜂窝板由上下玻璃钢面板和中间Nomex纸蜂窝芯3部分组成。图中为上下面板的厚度，2为蜂窝芯的高度；为Nomex纸的厚度，为正六边形的边长；、为所分析样件的尺寸。

图1 Nomex纸蜂窝板结构示意图Fig.1 Structural diagram of Nomex honeycomb sandwich panel

为获得其力学等效模型，采用蜂窝板理论将蜂窝夹芯板等效为均质正交各向异性板，获取其等效力学参数。等效过程分为两步，首先对纸蜂窝芯进行等效，然后基于等效蜂窝芯对夹芯板进行等效。对蜂窝芯的等效采用三明治夹芯板理论，其等效参数为

(1)

式中：下标、和分别对应图1所示模型的长(方向)、宽(方向)和高(2方向)；、、分别为Nomex纸的面内两个方向的杨氏模量和剪切模量；为Nomex纸的密度；c、c、c为蜂窝芯3个方向上的等效杨氏模量；c、c、c为蜂窝芯在3个面内的等效剪切模量；为蜂窝芯等效密度；c为面内等效泊松比。在等效蜂窝芯的基础上运用蜂窝板理论获得蜂窝夹芯板的等效力学参数：

(2)

(3)

式中：、为板的面内等效杨氏模量；、、为板的等效剪切模量；为等效泊松比；为夹芯板的等效密度；为上下面板的质量密度；可表示为

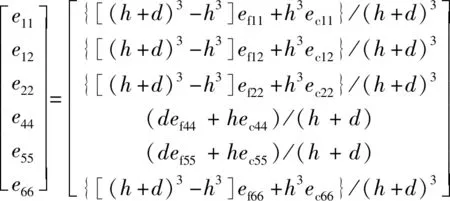
(4)

其中：f、c分别表示上下面板和芯层的刚度系数，可表示为

(5)

其中：、、分别为上下面板的杨氏模量、剪切模量和泊松比；为影响系数，根据工程实际或试验取0～1的数值，表明蒙皮横向剪切的影响程度。利用上述方法获取整流罩用的复合材料蜂窝夹芯板的等效力学参数，建立其等效力学模型，方便开展基于动力吸振器的减振降噪研究。

2 多模态耦合结构在分布力作用下的吸振器设计

现有基于动力吸振器的减振研究主要针对单模态频率开展动力吸振器参数设计。对于低频段模态密集的复杂结构，现有方法难以适用，需要发展考虑多模态耦合情况下的动力吸振器设计新方法，以实现结构的有效减振和声辐射的抑制。

对于分布力(,)作用下的薄壁结构，假设某频段内的响应主要由阶模态参与构建，且低频段模态存在相互耦合的特征。为了将适用于单模态的动力学吸振器设计方法应用于本文工况，构造新的维完备正交基来表示结构的阶模态振型，则有

(6)

式中：(,)为薄壁结构的第阶振型函数；(,)为新构造的完备正交基函数；表示对应的系数。使得分布力(,)在新构造的前-1阶完备正交基上投影为0，即满足

(7)

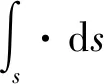
(8)

(9)

其中：为结构的第阶模态质量，且

(10)

联立式(7)和式(9)，可得特征模态(,)系数的表达式为

(11)

由此，通过本文首次提出的基于基变换模态空间内的降维理论，可以将由(,)函数张成的维结构模态空间内的动力吸振器优化问题降维成由(,)函数张成的一维空间的动力吸振器优化问题。一维空间内所对应的特征模态振型可表示为

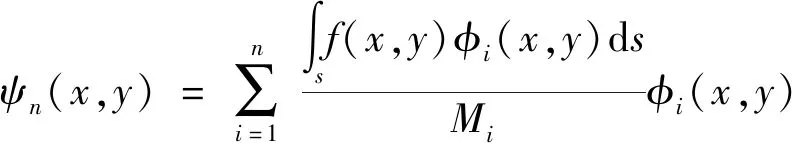
(12)

(13)

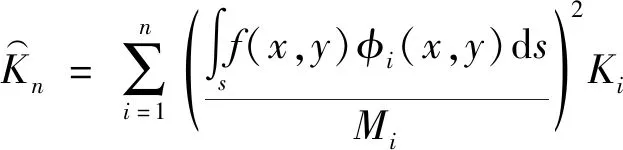
(14)

式中：为结构的第阶模态刚度。

根据单模态工况下包含动力吸振器的响应表达式：

(15)

式(15)可以重新写成

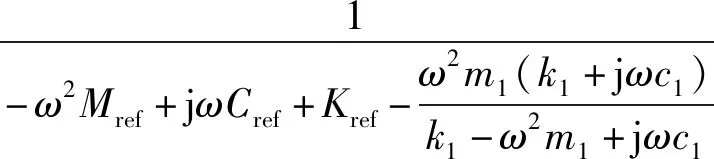
(16)

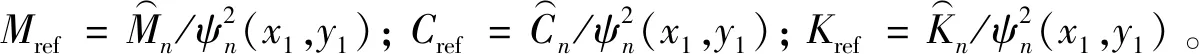
多模态耦合工况下动力吸振器的设计流程如图2所示，主要步骤包括：① 建立结构的有限元模型，并开展模态分析获取其模态频率和振型；② 构造新的正交基，将维空间结构动力学模型降维成新正交基下的单模态动力学模型；③ 根据单模态的极值位置确定动力吸振器布置位置；④ 建立单模态与单自由度主系统关于动力吸振器优化问题的联系，利用单自由度主系统动力吸振器优化问题中的定点理论获取动力吸振器的最优材料参数。

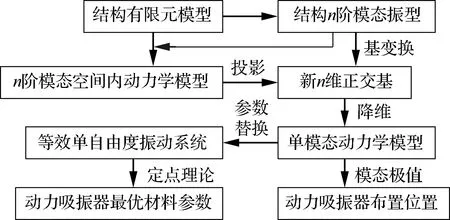
图2 结构的动力吸振器设计流程Fig.2 Design process of dynamic vibration absorber for structures

3 Nomex纸蜂窝板等效建模与模型修正

由于Nomex纸蜂窝板制备工艺的复杂性，使得实际蜂窝板结构的力学性能与图1所示理想结构存在差异，为了使得建立的等效模型能够真实反映结构的动力学行为，本节首先建立了Nomex纸蜂窝的初始精细化模型，并利用第1节中的理论方法获取等效参数，建立蜂窝板的初始等效模型。其次，利用如图3所示的蜂窝板试验件开展自由模态试验，基于实测模态数据的模型修正方法分别对初始精细化模型和等效板模型开展模型修正，获取修正后的精细化模型和等效板模型。最后，针对修正后的蜂窝板精细化模型及等效板模型展开声-结构耦合分析，验证等效板代替精细化模型进行声固耦合分析的可行性。

图3中所示试验件尺寸为855 mm×855 mm×40 mm，各初始力学参数如表1所示。自由模态试验中输入输出点以5×5矩阵均布在板上，边缘测点向内偏移50 mm以方便敲击。基于模态试验数据对等效板参数及精细化模型Nomex纸面内参数进行修正。修正前后材料参数如表1所示。从表1可以看出修正前后参数变化较大，这是由于蜂窝板材料的初始参数值与试验件的实际值相差较大所致，其中密度根据质量守恒直接得出，不参与修正。由表2及表3的模态参数对比可知，等效板模态振型与试验模态振型吻合得较为一致且模态频率误差控制在1%以内；等效板模型前3阶模态的模态置信准则(Modal Assurance Criterion，MAC)分别为0.91、0.91和0.93。因此，利用等效力学模型可以在大大降低复杂整流罩结构动力学分析计算量的同时保持较高精度。

表3 模态振型对比Table 3 Comparison of modal shapes

图3 蜂窝板自由模态试验Fig.3 Free modal test of honeycomb panel

表1 修正前后精细化与等效板模型材料参数Table 1 Material parameters of refined and equivalent plate model before and after correction

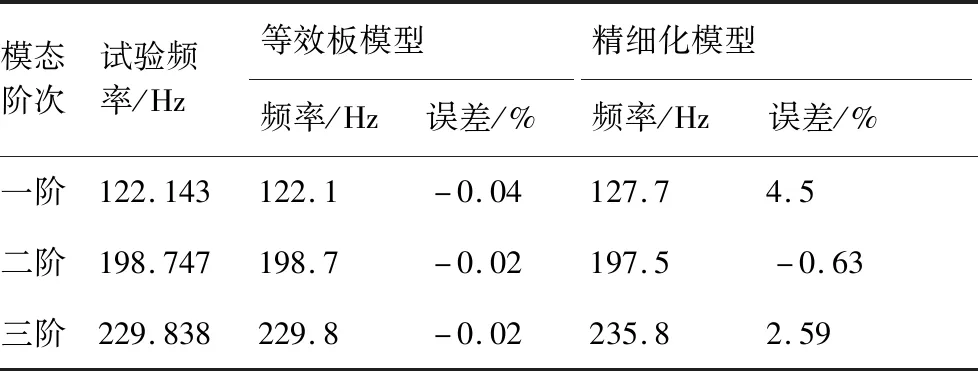
表2 模态频率对比Table 2 Comparison of modal frequencies

为进一步验证等效板模型代替蜂窝板精细化模型进行声振分析的可行性，由表1修正后等效板及精细化模型参数，建立图4所示的声振耦合分析模型。在对结构进行声学分析时，一般要求最大声学网格尺寸小于计算最高频率处波长的1/6。本文为获取前3阶模态频率对应的声学响应，将最高分析频率选为500 Hz。考虑到声在空气中传播的速度为340 m/s，模型网格最大尺寸应小于113 mm，实际建模中，将网格尺寸控制在50 mm。图5所示结果显示等效板模型及精细化模型辐射声功率曲线吻合较好，0～500 Hz声功率级RMS值分别为130.78 dB和130.71 dB，相差不到1 dB，验证了用等效板模型代替精细化模型进行声振分析的可行性。

图4 声振耦合分析模型Fig.4 Vibro-acoustic coupling analysis model

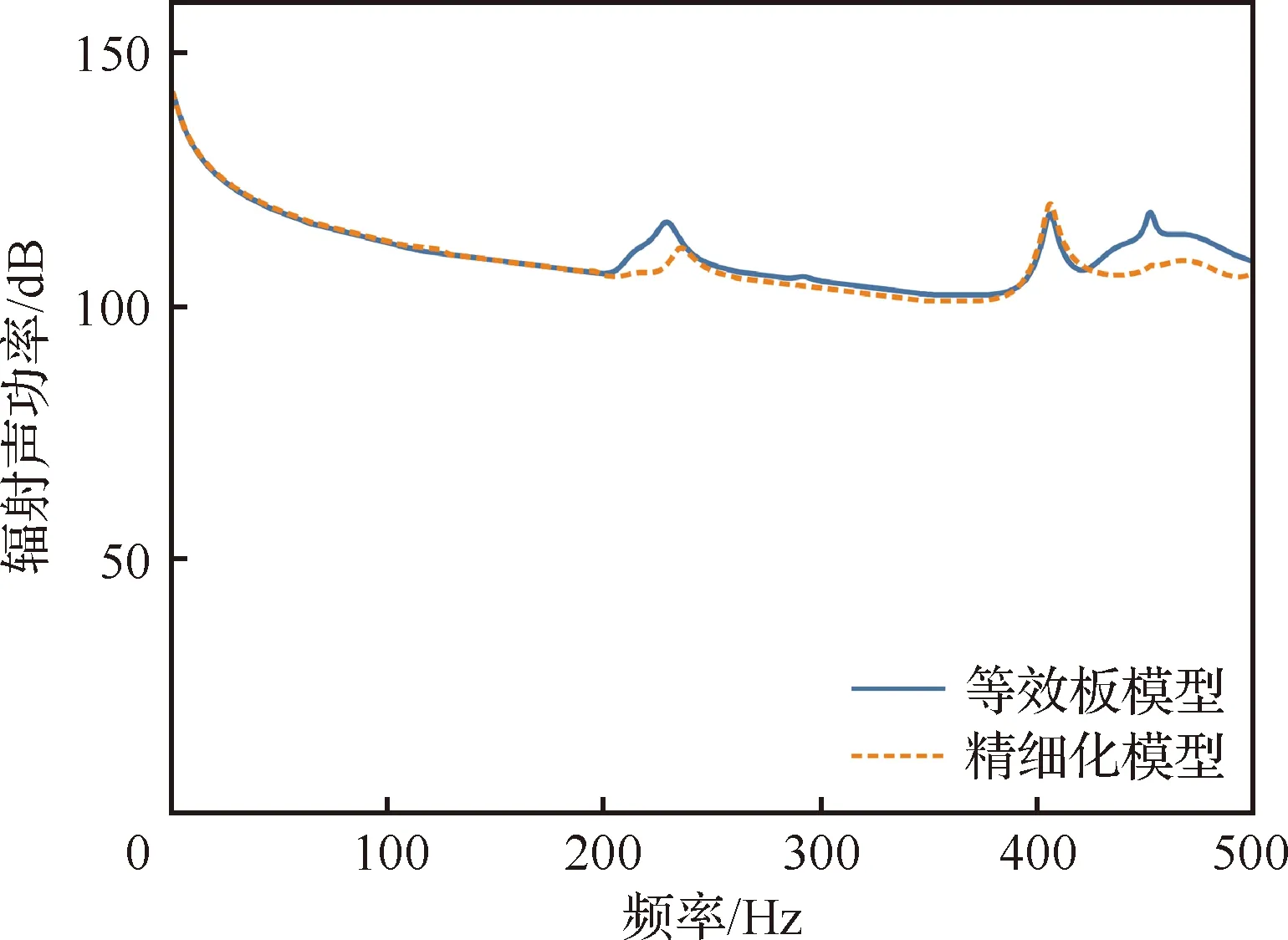
图5 辐射声功率曲线Fig.5 Radiation sound power curves

4 吸振器对整流罩的减振降噪效果

火箭发射阶段是整流罩环境最为恶劣的阶段之一。如图6所示气流经导流槽向上喷射会使火箭整流罩面临很大的气动噪声。本文考虑含有两个方向的导流槽作用，对火箭整流罩施加图7(a)所示分布力。由于整流罩球头段、冯·卡门锥段和倒锥段刚度较大，当研究低频段响应时，可用图7(b) 所示分布力近似代替整流罩实际载荷。

图6 导流槽Fig.6 Diversion groove

建立图8所示声学模型，其中结构网格为第3节建立的等效板模型，施加图7(b)所示单位分布力进行声-结构耦合分析。图9所示结果显示低频段整流罩内声学环境在35.9 Hz及90 Hz附近最为恶劣，图10显示90 Hz附近模态参与度较低，因此将35.9 Hz设为优化目标频率，添加动力学吸振器对该频段响应进行抑制。由于第2节中动力吸振器设计理论是针对振动响应优化得到的，而声学响应与振动响应之间并不存在线性关系，因此添加根据振动响应优化得到的动力吸振器之后虽然可以抑制设计频段内的声学响应，但有可能会在设计频率前或后出现新的声学响应峰。仿真结果表明添加动力吸振器后会使整体结构在50.5 Hz处出现一个新的响应峰值，为降低总体声学响应，将35.9 Hz和50.5 Hz两个频率作为优化目标频率展开减振降噪研究。

图7 整流罩载荷工况Fig.7 Load conditions on fairing

图8 整流罩声-结构耦合模型Fig.8 Structure-acoustic coupling model of fairing

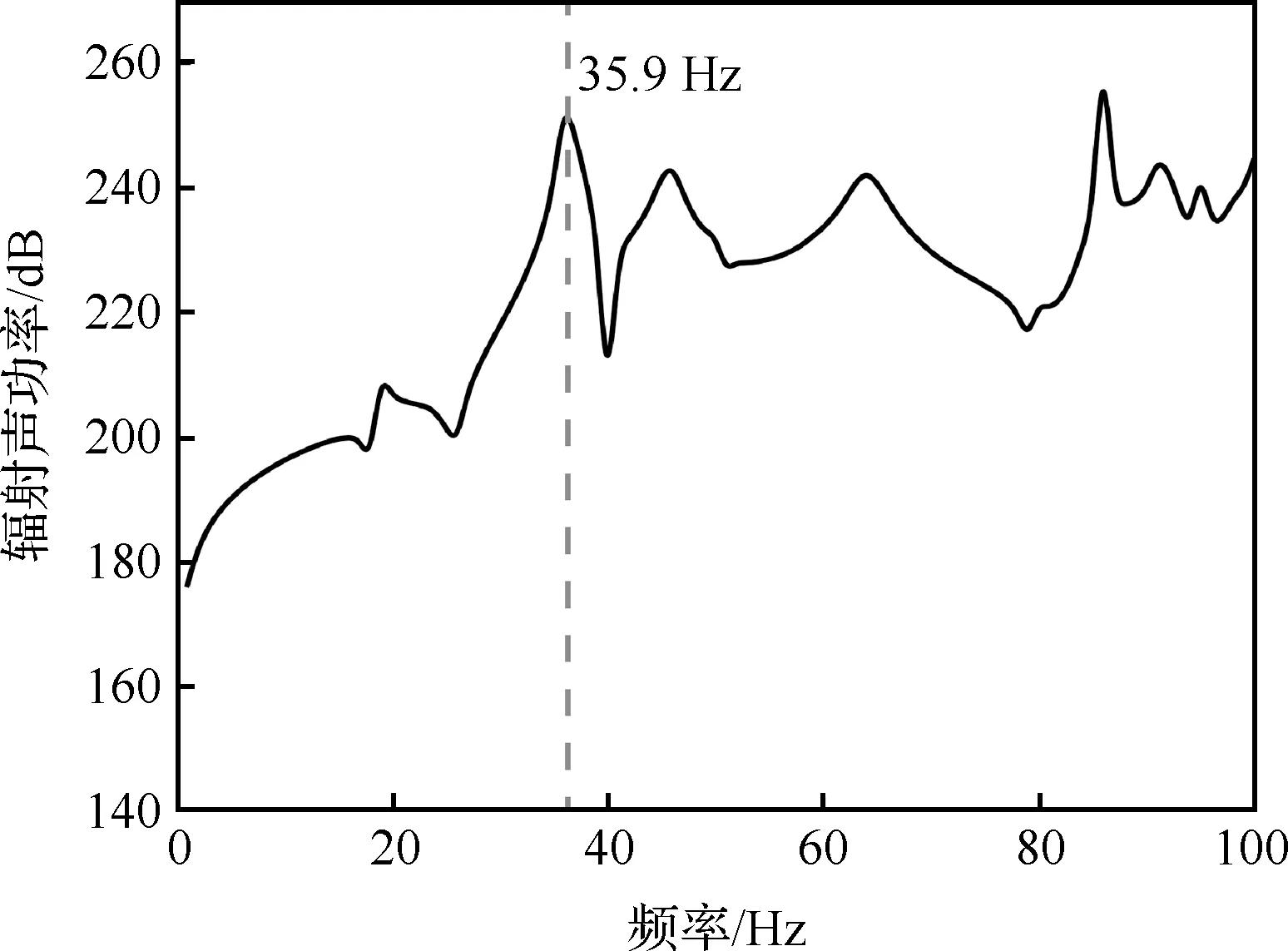
图9 整流罩辐射声功率曲线Fig.9 Radiation sound power curve of fairing

由式(12)可知，获取特征模态(,)之前需对整流罩结构模型各阶模态的参与度进行评估。图10所示0～100 Hz频段内结构模态的参与度曲线表明，在35.9 Hz处，整流罩三阶、四阶、五阶模态参与度较高；在50.5 Hz处，整流罩五阶模态参与度较高。整流罩结构模型中参与度较高的几阶模态振型如图11所示，三阶、四阶模态为对称模态，五阶、六阶模态为对称模态。当结构的响应由多阶模态参与时，可由第2节提出的理论在模态空间对响应进行降维处理。针对35.9 Hz 附近的响应，三阶、四阶、五阶模态参与度较高，因此将这3阶模态相关参数代入式(12)可得如图12(a)所示特征模态振型，同理可得针对50.5 Hz附近响应构建的如图12(b)所示特征模态振型。因此，可以针对图12所示两个特征模态振型，布置两种动力吸振器进行减振降噪。通过第2节中的降维理论将多模态参与的响应降维成单模态(特征模态)参与的响应之后，再经过参数替换可得到式(16)所示主系统振动响应表达式。由式(16)可知，两种动力吸振器的最优位置应分别为图12所示特征振型幅值最大处，最优参数可由定点理论直接得出，如表4所示。

表4 吸振器最优材料参数Table 4 Optimal material parameters of vibration absorbers

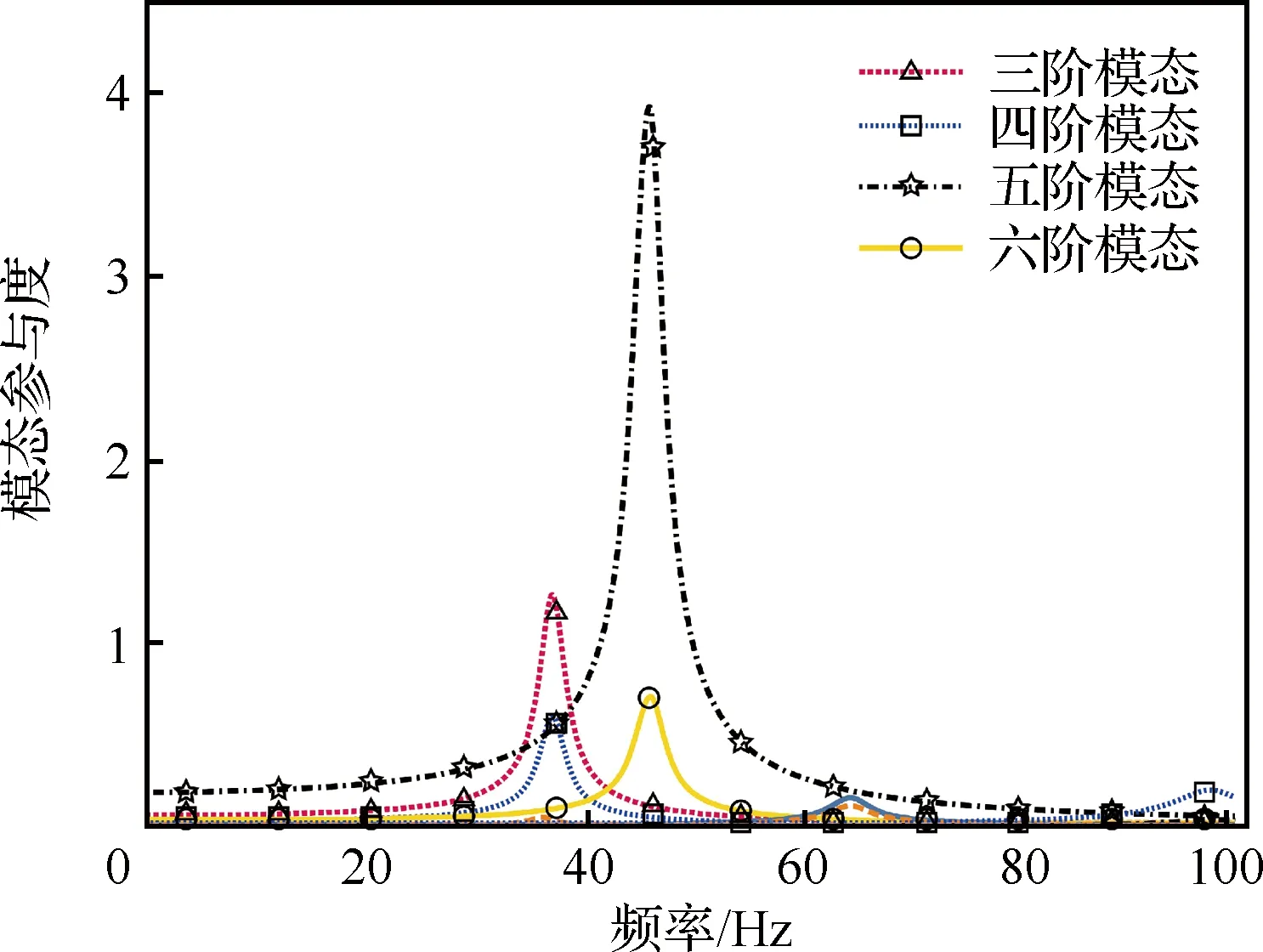
图10 模态参与度曲线Fig.10 Modal participation curves

图11 整流罩结构模型的模态振型Fig.11 Mode shapes of faring structural model

图12 特征模态振型Fig.12 Featured mode shapes

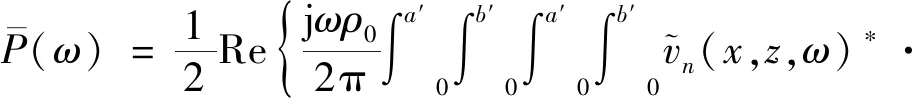
(17)

因此，为不破坏整流罩响应的对称性，在对称位置处同时布置动力吸振器，所添加吸振器总质量为14.6 kg。图13显示添加吸振器之后整流罩特征振型幅值处的振动位移在35.9 Hz处大幅降低，但在30 Hz附近出现了一个新的响应峰，这是由于添加吸振器后改变了整流罩的整体动力学特性，进而改变了整流罩的动力学响应。整流罩结构上图13所示响应点在30 Hz附近处于响应节点附近，添加吸振器后由于改变了整流罩的动力学响应，使得图13所示响应点在30 Hz附近处于添加吸振器整流罩耦合结构的响应峰值处，因此造成30 Hz附近添加吸振器结构之后响应量级反而增加的现象，但30 Hz附近整流罩的整体响应量级仍有所降低。图14显示辐射声功率在35.9 Hz处大幅降低，声功率级RMS值在0～100 Hz频段内从254.8 dB降至238.8 dB。实现了在增加质量不超过30 kg的前提下，0～100 Hz频段内整流罩内噪声水平下降3～4 dB的要求。