机器人精度补偿技术与应用进展

廖文和，田威，李波，李鹏程，张苇，李宇飞

1. 南京航空航天大学 机电学院，南京 210016

2. 南京理工大学 机械工程学院，南京 210094

新型航空器部件由于具有结构复杂、尺寸大、刚性弱、开敞性差等特点，尤其是新一代航空器要求具备长寿命、高安全、超高机动等跨代性能，对复杂部件的加工精度和效率提出了更高的要求。制孔质量一致性100%、铆接表面“零阶差”、快速批产等已成为世界航空制造业共性技术难题。传统的机床加工技术由于工作空间小、柔性化程度低，已经远远无法满足航空零部件型号多变、研制周期短、加工精度高的综合要求。工业机器人由于加工效率高、工作范围广、柔性化程度高等特点在汽车制造、机械加工等领域备受青睐。近年来，工业机器人因其具有重复精度高、可靠性好、适用性强等优点，已经在汽车、电子、食品、化工、物流等多个制造领域得到了广泛应用。随着机器人应用的拓展与深入，工业机器人开始进入一些高精度制造领域，如飞机装配、激光切割、柔性磨削等。波音、空客、洛克希德·马丁、NASA等世界航空航天巨头纷纷采用以机器人为核心的柔性制造技术与装备，作为解决上述难题的有效新途径，如图1 所示。在中国大力发展航空航天的时代背景下，以工业机器人为基础构建柔性制造单元或柔性生产线，实现产品快速化、柔性化、自动化生产，对航空航天制造业生产模式转型升级、提升装备制造能力和产品性能具有重要意义。

图1 国外航空装备机器人制造系统Fig.1 Foreign robotic manufacturing system in aviation equipment

绝对定位精度和重复定位精度是工业机器人两项重要的精度指标，前者反映了机器人实际位置与理论位置的偏差程度，后者则体现了机器人到达同一位置的准确程度。一般来说，工业机器人的重复定位精度较高，最高可达±0.013 mm，因此通过传统示教编程的方式引导机器人末端执行器执行重复性作业任务也能够达到较好的精度。然而，与传统制造行业不同，航空制造业中的飞机大部件加工与装配需要更高的质量和精度，对机器人装备的结构、可靠性、开放性和精度等核心性能提出了更高要求。飞机部件往往尺寸较大，连接孔及连接件的数量多，编程工作量大导致工作周期长，也更易引发碰撞干涉等问题；同时人工示教的定位精度取决于工人的技术水平，很难保证飞机装配所需的孔位精度要求(如孔的位置度要求±0.5 mm，法向精度要求±0.5°)。为解决上述难题，飞机装配普遍采用离线编程，节省工作量并提升装配效率。离线编程的作业方式极大依赖机器人的绝对定位精度，而机器人绝对定位精度仅为±1～2 mm，难以满足飞机装配的精度要求。因此，工业机器人的绝对定位精度成为制约其应用于航空航天等高端制造业的技术瓶颈。尤其是随着新一代大飞机和高性能军机等高端产品对加工制造精度要求的不断提高，其瓶颈效应越发明显，对高精度工业机器人的需求日益迫切。因此，如何提高机器人的定位精度已成为机器人学术界和航空制造部门无法回避且必须解决的问题。

综上所述，工业机器人在航空制造业具有广泛的应用前景和显著的应用价值。但是，航空产品高质量和高精度的迫切需求，与目前中国工业机器人作业系统精度低之间的矛盾日益突出，已成为制约其在中国乃至全世界航空制造业中应用的主要瓶颈。针对目前国内外的机器人定位精度低的问题，本文分析与总结了国内外学者提出的定位精度补偿技术。第1节对机器人的定位误差源进行梳理、建模与分析；第2节将机器人的精度补偿技术分为离线标定与在线标定两种方法,详细阐述并对比分析，探讨了两种方法的优缺点与适用范围；第3节针对现有的精度补偿技术在各个领域的应用进行介绍；第4节分析了目前机器人精度补偿技术存在的问题与未来的发展趋势并对文章进行总结。

1 机器人定位误差源

目前，提升机器人精度的方法主要有两种，一种是在机器人加工制造阶段的误差预防技术，一种是机器人装配完成后的精度补偿技术，对误差源进行梳理、建模与分析是上述两种方法的研究基础。由于机器人的制造装配误差、传动控制误差等因素均会使机器人实际的位姿与理论计算结果有所偏差，因此，有必要研究机器人定位误差的作用规律，以便于后续为机器人精度补偿提供理论依据。

在误差源梳理方面，根据误差的表现形式，研究人员将机器人的定位误差源划分为几何误差、非几何误差以及系统误差。具体分类与原因如表1所示，几何误差是可以用几何量表示的误差源，主要指机器人运动学模型的参数误差，即由机器人各连杆杆长、连杆偏置以及各关节转角、关节扭角等参数误差造成的连杆坐标系传递误差，例如机器人在加工制造、装配时关节减速器的安装位置误差，又如关节零位在出厂标定时的误差等，均会导致机器人运动学几何参数产生相应的误差，进而影响机器人的定位精度。非几何误差是难以用几何量表示的误差源，主要包括机器人关节的柔度、相对运动产生的摩擦、关节间隙、动力学误差以及热效应等。系统误差指在机器人运行时所产生的控制误差、数值截断误差以及测量误差等。Nubiola和Bonev将机器人末端位姿误差的误差源分为环境误差、参数误差、测量误差、计算误差和应用误差。参数误差包括零部件制造装配误差引起的运动学参数变化、动力学参数的影响、摩擦、关节间隙和迟滞等非线性误差；测量误差主要为关节位置传感器的非线性特性引起的误差；计算误差主要为计算圆整误差和稳态控制误差；应用误差主要为安装等引起的误差。Collins和Robinson梳理了10种引起机械臂末端位姿误差的误差源，并分为系统误差和随机误差两类。其中，系统误差包括装配引起的运动学参数误差、刚度模型不确定引起的柔性误差、热膨胀模型不确定引起的未补偿热失真、热梯度变化引起的未建模热失真；随机误差包括齿轮啮合间隙误差、编码器导致的控制误差、装配引起的随机误差、摩擦引起的齿轮扭转变形、由轴承引起的关节轴线的偏移、零位误差。此外，国内任永杰等也将影响机器人定位误差的因素按照来源及相互作用机理分成4类：参数因素、负载因素、结构因素、环境因素。可以看出机器人的误差来源错综复杂，研究人员一直以来对其进行分类分析以更好地研究误差源对机器人末端位姿误差的影响，从而开展机器人定位精度的补偿技术研究。

表1 误差来源分类总结Table 1 Summary of classifications for sources of errors

在误差建模与分析方面，其意义在于建立误差与末端执行器位置偏差的数学关系模型，以反映误差源是否影响以及如何影响机器人输出精度，从而更好的理解机器人的行为，进而为机器人精度补偿提供指导。在几何误差方面，基于D-H方法建立的误差模型被广泛采用。Judd和Knasinski认为关节转角误差对机器人定位精度的影响最大，所引起的误差占定位误差均方差的90%；Shiakolas等对PUMA560机器人的研究分析发现关节转角误差大约占机器人位置误差的90%左右。在非几何误差方面，文献[16]在考虑了运动学参数误差的基础上，对机器人影响较大的非几何误差即由连杆自重产生的连杆变形进行建模；Elatta等对机器人的非几何误差建模进行了总结分析，得出非几何误差约占总误差的10%，其中非几何误差中的关节柔度误差要大于连杆柔度误差，非几何误差中的热效应只占总误差的0.1%。可以看出，结合几何误差与几何误差综合建模分析的方式应用广泛，如从机械制造、装配误差和关节间隙3个方面具体建模、考虑关节的垂直误差以及连杆的平行度误差；考虑环境温度、电机发热以及关节摩擦热、关节反向误差、动力学因素、摩擦因素、关节间隙等。此外，考虑到机器人运动过程中影响定位精度的误差因素十分复杂，通常导致机器人的参数不确定，因此机器人参数不确定性的误差建模与分析方法得到发展，Wu和Rao建立了包含机器人参数和关节间隙的误差概率模型，采用蒙特卡洛方法对定位精度进行可靠性分析；王铁军将ADAMS软件作为分析平台，考虑连杆尺寸误差和关节间隙误差建立了机器的运动仿真误差模型，并分析了随机误差对其动态可靠性的影响，一定程度上为机器人定位精度补偿指明了方向。

几何误差、非几何误差以及系统误差都将导致机器人的参数或机械结构发生变化，均需要针对性的分析进行补偿。机器人几何误差是造成机器人位置误差的主要影响因素，但是非几何误差和系统误差是机器人定位精度无法进一步提高的重要原因。综上所述，众多不确定误差源使得很难建立精确的机器人定位误差模型，需要考虑更加全面的不确定因素的影响，深入挖掘引起机器人定位精度低下的误差影响机制、研究适合工业机器人的精度补偿模型，才能有效地提升机器人定位精度。

2 机器人精度补偿技术研究现状

机器人精度补偿技术是指在装配完成后运用测量工具并结合数值算法消除机器人误差，进而调整预设参数直到机器人精度满足要求的方法。为突破机器人加工制造过程中的精度问题，国内外的学者和技术人员提出了多种提高机器人运动精度的方法，取得了大量的研究成果。根据精度补偿方法原理上和思路上的差异，主要分为离线标定和在线补偿两类。前者是指运用测量工具预先获取机器人的定位误差，进而在机器人工作时仅通过补偿算法提升机器人的定位精度。后者则需要在工作时依靠外部测量工具如光栅尺、激光跟踪仪等检测机器人关节或末端的实际到达位置，进而实时补偿定位误差。以下从离线标定技术所包含的运动学标定、非运动学标定、物理约束标定以及在线补偿技术所包含的关节编码器反馈、激光跟踪仪反馈、视觉伺服反馈等方面进行详细分析。

2.1 离线标定技术

机器人离线标定方法基本原理是在机器人工作空间内测量若干关节构型的末端定位误差，建立机器人运动学误差模型，辨识机器人运动学参数误差，或者建立机器人笛卡尔空间或关节空间下的误差映射。将得到的误差模型或者误差映射预置到机器人补偿算法中，实现目标点定位误差的估计与补偿，进而提高机器人的定位精度。经过离线标定的机器人在实际作业中不需要借助外部测量工具，是目前研究最广泛、应用最普遍的方法。机器人离线标定方法根据其标定原理或者误差测量方法的不同，分为运动学标定、非运动学标定、物理约束标定。

2.1.1 运动学标定技术

运动学标定法一般采用D-H模型对机器人进行运动学误差建模，并采用离线标定的方式，获取真实的模型参数，从而提高机器人的精度。这类方法现在比较成熟，主要思想为建立描述机器人几何特性和运动性能的数学模型，随后测量机器人末端执行器在世界坐标系下的多点位置，继而识别机器人关节运动学参数误差，带入机器人运动学模型以最小化机器人定位误差的估计值与实际值之间的残差，最后修改机器人控制器参数，使得控制器内部的机器人运动学模型与实际运动学模型近似，完成误差补偿。通常情况下，机器人的运动学标定过程通常按照4个步骤进行，分别是建模、测量、参数识别和误差补偿。

1) 运动学模型

目前机器人使用的运动学建模方法主要包括D-H法(Denavit-Hartenberg)、MD-H法(Modified D-H)、S模型、CPC模型(Complete and Parametrically Continuous)、零位基准模型(Zero Reference Position Model)以及指数积模型(POE，Product of Exponentials)等。D-H模型是最经典也是应用最广泛的运动学模型，虽然D-H模型意义明确且使用方便，但其描述的是机器人的理论运动学模型，不能完全满足机器人运动学标定的需求。这是由于机器人运动学误差模型基于微小位移假设，当机器人存在轴线相互平行或近似平行的两个相邻关节时，若使用D-H模型定义关节运动学参数将出现奇异，某些运动学参数将随着其他参数的微小变化而发生突变，所以无法满足微小位移假设。Hayati和Mirmirani对D-H模型进行了改进，提出了MD-H模型，通过在相邻的平行关节之间增加一个绕轴旋转的运动学参数，从而避免了参数的突变，解决了D-H模型的奇异性问题。Alici和Shirinzadeh利用MD-H模型建立了Motoman SK 120型工业机器人的运动学模型并进行了补偿。Nubiola和Bonev对ABB IRB 1600型工业机器人建立了包含几何参数和非几何参数的29参数模型，其中几何参数是根据MD-H模型建立的。另外，Stone等重新定义了连杆坐标系的建立规则并据此提出了S模型，该模型中每个连杆通过6个参数进行描述，包括3个平移参数和3个旋转参数。Zhuang等通过研究认为运动学模型只有同时满足“完整性”和“参数连续性”才能够适用于机器人运动学标定，因此基于该思想提出了CPC模型。Kazerounian和Qian改进了Gupta提出的零位基准模型，在该模型的连杆参数中去除了相邻关节的公法线方向，取而代之的是各关节轴线在以零位为基准时的位置与方向，解决了模型的奇异性问题。Okamura和Park提出了指数积模型，机器人的运动学模型由一系列指数矩阵的乘积进行表示，可以实现各关节的运动学参数的平稳变化，从而避免了参数的突变。Chen等提出了局部指数积模型，使用局部坐标系对机器人各个关节进行了描述。当机器人自由度较高时， POE运动学建模方法更高效、更有条理。尽管研究者针对D-H模型的奇异性问题先后提出了诸多建模方法，但D-H模型凭借其物理意义明确、建模过程简单、通用性较强的优势，在机器人工程及学术领域仍然广为使用。

2) 误差测量与采样点规划

误差测量是机器人精度补偿技术中的关键步骤，也是最繁琐和最耗时的步骤之一。机器人精度补偿的效果直接取决于误差测量的质量，因为通过高精度测量设备获取的机器人实际定位误差数据是参数识别和误差估计的原始依据。误差测量的质量主要与所使用的测量工具和测量方法相关。实际应用中，可以通过零点标定工具、球杆仪、经纬仪、坐标测量机和激光跟踪仪等对工业机器人的定位误差进行测量。这些测量仪器的对比如表2所示，在众多测量设备中，激光跟踪仪由于其易携带、实时跟踪、操作简便、精度高等优点而成为机器人标定中应用最广泛的测量设备之一。

表2 机器人校准仪器性能比较Table 2 Performance comparison of robot calibration instrument

采样点的选取对精度补偿的最终精度具有显著的影响。一方面，机器人误差模型的拟合精度与采样点的数量和位置有关，如果测量的采样点数量过少，或者采样点的位置在机器人工作空间中过于集中就会影响精度补偿的最终效果。另外，采样点的测量是机器人精度补偿技术中耗时最长的一个步骤，如果采样点数量过多，将导致测量时间过长，而精度补偿的最终精度却又无法随采样点数量的增多而无限提高；同时，在此测量过程中会存在环境温度变化和测量设备零位漂移等随机误差，反而可能对精度补偿的最终精度造成不良的影响。因此，如何确定合适的采样点数量和采样点位姿，以平衡采样效率与最终补偿精度之间的矛盾，是机器人精度补偿技术中需要解决的一个关键问题。Borm和Meng将控制理论中系统能观性的概念引入机器人精度补偿技术中，并使用机器人雅可比矩阵的奇异值之积作为计算机器人运动学参数的能观性指数，认为只有当采样点集合能够最大化运动学模型中误差参数的能观性时，才能最小化运动学参数的识别误差。Joubair和Bonev通过试验证明了能观性能够获得最佳的标定精度。Zhuang等研究发现参数误差造成的影响的上限值与雅可比矩阵条件数成正比，因此将雅可比矩阵条件数作为可观测度指标，将最优采样点的选择问题转化为研究雅可比矩阵条件数的问题。并提出一种模拟退火算法获得机器人最优采样点，使用冷却进度表加快迭代速率，该方法可以克服微分算法陷入局部最小值问题。国内在最优采样点规划方面，丁学亮采用文献[49]提出的可观测度指标并基于DETMAX算法选择最优测量位姿，规划出最优采样点。由此可见，机器人采样点的选取十分重要，目前的采样点优化方法主要是以运动学参数的能观性作为采样点优劣的指标，曾远帆等提出最优采样点的特征和数学模型如图2所示，基于NSGA-II的方法对采样点多目标优化，提出面向非运动学参数的采样点优化方法。洪鹏等在基于误差相似度的精度补偿基础上，提出均匀网格最优采样点的选择方法，并通过试验和统计分析的方法优化采样点网格。

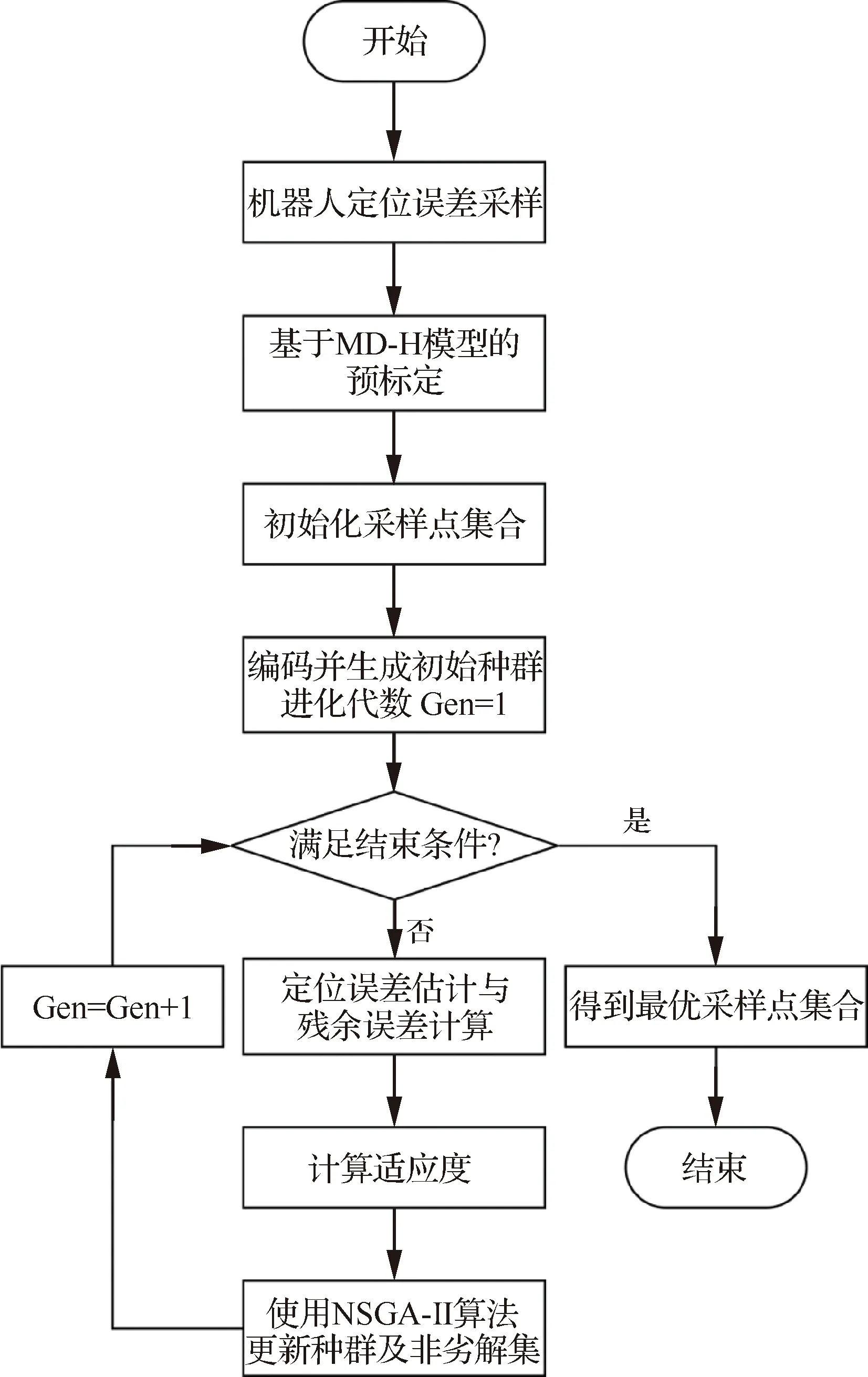
图2 基于NSGA-II 的采样点多目标优化算法流程图[54]Fig.2 Flowchart of multi-objective optimization of samples based on NSGA-II[54]

3) 参数误差识别

运动学参数误差识别是运动学模型标定的最终方法。在运动学模型建立完成之后，通过采集误差信息完成初始数据的制备。最终通过数值优化等方法优化相关参数，使各项机器人运动误差达到最优解，并使采集得到的数据点误差和拟合误差之间达到数值最小化。最小二乘法由于求解简单，因而被广泛运用到各类回归模型中，进而被应用于运动学误差辨识，然而在辨识矩阵接近奇异时，会极大地影响最小二乘法的辨识精度，因此许多学者对优化算法进行研究。在最小二乘法的改进算法中，L-M(Levenberg-Marquardt)算法广泛地应用于机器人运动学标定领域。田威团队利用L-M算法对机器人几何误差和关节柔度误差进行识别，并提出了空间网格化的变参数误差模型，有效解决了参数误差空间分布不均匀的问题。模拟退火算法和极大似然估计法也在一定程度上应用于机器人运动学参数识别与求解。Renders等对机器人的运动学参数进行了最大似然估计，虽然计算过程较为简单，但全局精度较低。

扩展卡尔曼滤波器也能够用来解决机器人运动学参数识别问题。Park等分别对7自由度机器人和4自由度机器人使用扩展卡尔曼滤波器进行运动学误差估计，并进行了仿真和试验。Omodei等基于5自由度PUMA机器人，对比分析了非线性优化、线性迭代和扩展卡尔曼滤波在参数识别中的应用效果，发现扩展卡尔曼滤波器能够求出参数误差的不确定度等额外信息，且能够获得较高的效率。扩展卡尔曼滤波法在收敛速度、可靠性和对辨识结果的评估上都有着一定的优势。

许多用于求解非线性问题的智能算法，尤其是人工神经网络，也被用于机器人运动学参数识别。Zhong等分别应用递归神经网络和多层前馈神经网络识别了PUMA机器人的参数误差，将机器人的定位精度提升至重复定位精度的水平。Jang等采用径向基函数神经网络对DR06工业机器人的几何误差和非几何误差进行了识别，将机器人的最大定位误差由5.8 mm减小至1.8 mm。采用神经网络进行机器人运动学参数识别的缺点在于其求得的最优解往往是局部极值，导致识别精度较低。

4) 误差补偿

误差补偿是机器人运动学标定的最后也是决定性的步骤，其基本原理是在识别待补偿点的位姿误差之后，通过修正机器人的控制参数或者改变机器人的控制方法，使机器人根据相应的补偿量进行定位，以提高机器人的定位精度。关节空间补偿法和微分误差补偿法等方法是现阶段较为常用的误差补偿方法。关节空间补偿法是将参数辨识得到的运动学参数误差带入机器人运动学模型中，从而得到修正后的运动学模型，然后将机器人待补偿点在笛卡尔坐标下的位姿通过运动学逆解，转化到机器人关节空间中，直接将新模型计算得到的关节运动值作为控制量，在控制系统中进行控制。微分误差补偿法是基于微分变换的思想，将机器人定位误差看作微小位移，并用各关节参数的微分变换表示出来，与关节空间补偿法不同的是，微分误差补偿法是计算各关节轴的补偿量，在控制机器人进行定位时对各轴进行相应的偏移，以实现机器人位姿误差的补偿。关节空间补偿法的缺点在于要求机器人控制系统具有较高的开放性以修改控制参数，但多数情况下技术人员难以获得较高的修改权限；另外，若需要对机器人本体和控制器进行改造，对于大多数商用机器人，改造成本也较高。

2.1.2 非运动学标定技术

与运动学参数标定相对应的是非运动学标定法，该方法无须参数建模和误差识别，通过神经网络、空间插值等方法对局部空间内位姿误差进行估计与补偿。影响机器人定位误差的因素很多，这些因素相互耦合，影响机制复杂，难以构建一个包含所有误差源的精确模型。因此许多学者将研究目标集中在构建一个通用的模型预测误差，通过将末端定位误差与关节转角或空间位姿形成映射关系进而构造相应的误差模型。

1) 神经网络法

神经网络是近年发展起来的一门新兴技术，具有自学习能力强、自适应范围广、容错率高等优点，能够完成自适应推理，在工作过程中也可以通过多次自适应学习提高识别效率，通过模拟人脑的神经网络能够较好的构造机器人末端定位误差与关节转角或空间位姿的关系，因而被广泛地运用在非运动学模型标定中。

这类方法通过多组不同关节角度以及对应末端执行器的空间位姿为输入，利用这些信息来训练生成基于神经网络的控制网，对关节角进行对应的补偿，以此达到提高定位精度的目的。文献表明该方法有很好的定位精度提升效果，图3 为Wang等利用神经网络模型得到的位置误差对目标位姿进行补偿。国内也使用神经网络方法对机器人的误差进行预测与补偿，如图4所示为Li等使用基于粒子群优化深度神经网络实现的机器人误差预测和补偿。上述方法虽然克服了参数不足以及运动学建模复杂的缺点，有效提高了机器人最终的定位精度，但是仍然存在标定过程计算量大、研究不够成熟、耗费时间过长等缺点，导致其仍然无法广泛地应用在实际场合中，无法形成一套可操作系统化的标定方法。

图3 位置误差估计的神经网络[67]Fig.3 Neural network for position error estimation[67]

图4 基于遗传粒子群算法优化深度神经网络的机器人定位误差补偿[69-71]Fig.4 Robot positioning error compensation based on GPSO-DNN[69-71]

2) 空间插值法

除神经网络外空间插值法也能较好的补偿机器人定位误差，该方法的定位误差标定通常分为以下几步：网格划分、误差测量、空间插值。现有学者提出了模糊插值方法与双线性插值方法，结果表明此类空间插值方法标定效果优于运动学标定技术。

此外，周炜等提出了空间相似性的概念，将工作空间划分为若干空间立方体，通过采集立方体顶点的误差信息并使用反距离加权法建立误差模型，利用网格顶点的定位误差实现网格内部的点位插值。Zeng等基于机器人误差相似度特性建立了插值补偿方法，如图5所示，通过变差函数分析关节转角与定位误差的相似关系，并通过线性无偏最优估计模型对目标点位进行插值补偿。为了达到更好的标定效果，何晓煦等将机器人运动学标定后的残余误差做变差函数分析，证明残差存在空间相似性并构建了残差的线性无偏最优估计模型，先通过运动学标定补偿几何误差再通过误差相似度模型补偿残余误差。Cai等发现，在误差相似度概念的基础上通过普通克里格法对工业机器人误差建模，能有效提高补偿精度。

图5 基于误差相似度的误差识别与补偿方法流程图[7]Fig.5 Flowchart of error identification and compensation method with error similarity[7]

可以看出，机器人非运动学标定方法是一种综合性的误差标定方法，避免了复杂的机器人误差建模过程，克服了机器人运动学标定的参数识别不准确的问题，通过构建误差映射关系来实现目标位姿定位误差的估计与补偿。因此，该方法从原理上可以视为一种数值估计方法，数值估计所使用的数据越多，标定精度越高。但是该方法直接将位姿误差归结为关节角误差，不去考虑关节型机器人结构特点与运动特性，无法更好地分析机器人的位姿误差分布特点与规律。

2.1.3 物理约束标定技术

通常情况下，机器人运动学标定和非运动学标定需要配备高精度的外部检测设备对机器人末端定位误差进行测量，且需要相关技能人员来操作测量软件，在某些场合下限制了其应用。因此，研究者们也探索机器人物理约束标定方法，无需任何测量设备即可完成机器人标定。其主要思想是机器人末端与球、平面、单点、距离等物理约束接触来构建约束方程，然后基于约束方程建立机器人误差模型，根据该模型完成机器人参数标定。Gaudreault等通过机器人末端的3个数字千分表与其工作空间内的约束球多次接触，基于球约束和关节转角建立位置约束方程，完成机器人运动学参数标定，如图6(a)所示。Joubair和Bonev使用机器人末端上高精度探针触碰立方体的4个约束平面以建立平面约束方程，进而对机器人几何误差、关节柔度误差、机器人基坐标系和工具坐标系误差进行辨识，将机器人距离误差最大值由标定前的1.321 mm提高至0.274 mm，如图6(b)所示。He等利用点约束来提高六轴工业机器人的精度，通过控制机器人以不同姿势到达相同位置来校准机器人参数，如图6(c)所示。Liu等使用激光工具和便携式位置敏感设备，提出了一种用于关节偏移校准的基于虚拟线的单点约束方法。Wang等和Ha分别使用激光跟踪仪和激光位移传感器测量了机器人多个TCP位置之间的相对距离以及多个TCP位置相对于基准平面的高度值。

图6 物理约束标定法Fig.6 Physical constraint calibration method

可以看出，机器人物理约束标定方法的标定精度很大程度上依赖于末端传感器的灵敏度，且对物理约束的加工精度要求很高，同时，该方法在物理约束区域附近补偿效果良好，在机器人工作空间的其他区域的补偿效果欠佳。

以上几类精度补偿方法都是离线校准方案，无法在机器人实际工作中对动态误差进行补偿，精度提升性能有限。

2.2 在线补偿技术

上述的机器人离线标定方法通过辨识机器人运动学参数误差、构建定位误差映射或者建立物理约束方程，实现机器人末端定位误差的补偿，具有较强的通用性与实用性。但是从上述分析可知，机器人离线标定方法高度依赖于机器人的重复定位精度，实际上机器人单向重复定位精度很高，但是多方向重复定位精度较差。也就是说，由于机器人多方向位姿准确度较差，在上述机器人离线标定方法的误差测量环节中，机器人从不同方向运动到同一采样点的误差不同，即采样点误差本身具有不确定性。因此，离线标定方法无法进一步提高机器人精度补偿效果。

在线补偿法是指利用外界高精度的测量设备对工业机器人的运动进行实时反馈，使机器人在工作过程中可以不断调整末端姿态直至理想状态。根据误差反馈所采用的装置，将机器人在线补偿方法分为关节编码器反馈技术、激光跟踪仪反馈技术以及视觉伺服反馈技术3种方式，如图7 所示。其中关节编码器反馈技术是一种半闭环的补偿方法，将待补偿的点位误差从笛卡尔坐标系转化为关节修正值；采用视觉伺服或激光跟踪仪等设备进行末端位姿反馈是一种全闭环补偿方法，即直接测量笛卡尔空间的误差从而实现机器人末端位姿的修正。

图7 在线反馈补偿技术Fig.7 Online feedback compensation

目前国外一些机器人公司已经将关节编码器反馈技术应用在机器人精度提升上，如Fanuc和Electroimpact(EI)均将关节编码器应用到机器人的补偿当中，但是需要进一步修改机器人内部的控制系统。Saund和Devlieg以及Möller等将光栅尺作为关节编码器，并通过西门子840D数控系统控制关节电机，有效降低了机器人的定位误差。但是由于对机器人控制器进行改造的技术难度较高，其原有控制器对外部编码器的开放性又较差，Liu等设计PD控制器，将半闭环控制系统放置在机器人控制系统外部，通过关节位置偏转控制接口实现对机器人的关节控制，综合补偿过后的定位误差可降低至0.2 mm以下。此外，考虑到运动方向所导致的关节回差对机器人精度的影响，许多学者在机器人关节处安装外部编码器，通过内外编码器来确定或者消除关节回差。Zhang等考虑到关节回差对机器人多方向度的影响，在KUKA KR210前三轴关节安装光栅尺，并用切比雪夫多项式进行关节插值补偿，使制孔精度达到0.25 mm。由此可见，使用关节编码器反馈技术结合数控系统来提高工业机器人的精度在工业中具有广泛应用，但由于改造机器人控制器比较困难，很多研究者通过内部控制器与外部控制器相结合的方式进行关节控制，此外关节编码器反馈技术可以更好的对机器人多方向准确度进行修正。

基于末端伺服的机器人补偿技术能够大幅度提高机器人的定位精度，其主要思想为在机器人末端增加基于视觉或者激光跟踪仪的靶标，从而获得当前末端的实际位姿，再通过与目标位姿进行比较，由控制系统根据偏差对机器人进行位姿调整，从而达到规定的精度要求。激光跟踪仪在机器人末端全闭环反馈技术中应用广泛，Droll针对机器人路径修正的问题，提出采用激光跟踪仪进行路径在线补偿的方法，利用D-H模型来计算笛卡尔坐标空间中的修正值，并映射到机器人关节上，实现快速路径修正，该方法实际上是利用辨识出的运动学参数将笛卡尔空间的误差在关节空间中进行补偿，并未实现完全意义上的在线全闭环反馈。国内曲巍崴等以及史晓佳等均采用激光跟踪仪对机器人末端位姿进行实时的反馈修正，补偿后定位精度可达到±0.2 mm以内。基于激光跟踪仪的补偿技术精度最高，加工时位姿保持能力强，同时也存在成本高、对工业现场要求高、末端执行器设计复杂以及通用性差等缺点。

随着计算机图像处理能力的提升，视觉测量系统的测量频率也逐渐提高，研究人员提出基于视觉引导的机器人控制方式，也称为视觉伺服。视觉伺服系统的在线补偿架构一般由视觉系统、控制策略和机器人系统组成。要实现全位姿动态测量需求，视觉是一种有效的测量方法，常见的视觉伺服方法有基于图像的视觉伺服、基于位置的视觉伺服和混合视觉伺服。基于图像的视觉伺服(Image-Base Visual Servoing，IBVS)如图8(a)所示，采用图像特征参数直接描述机器人末端执行器与目标位置之间的误差；基于位置的视觉伺服(Position-Based Visual Servoing，PBVS)如图8(b)所示，需要将视觉信息与机器人运动学模型、几何目标模型和相机模型等知识结合使用，通过提取、解释和变换图像特征，来获取目标相对于视觉系统的位姿信息，控制机器人减小当前位姿与期望位姿的误差；混合视觉伺服(Hybrid Visual Servoing，HVS)如图8(c) 所示，也称2.5D视觉伺服，将以上两种视觉伺服方法综合，利用三维信息减小机器人位置误差，利用二维信息减小机器人姿态误差。IBVS控制方法采用的是二维图像，缺乏深度方向的信息，对机器人全位姿精度的控制能力有限。HVS 控制方法需要对单应性矩阵分解计算，计算困难，计算量大，难以用于高频率的实时位姿控制。PBVS则更加适用于引导机器人移动。目前一些研究者将基于位置的视觉伺服成功地应用在了机器人的在线精度补偿当中，Schneider等通过光学测量设备对机器人末端和微型执行器进行实时检测，实现机器人末端工件与微型执行器上的刀具之间相对位置关系的在线修正。该方法在机器人末端受力较大的情况下具有较高的加工精度。Shu等通过双目视觉设备实时检测末端的位姿，根据位姿误差对Fanuc M20-iA型机器人进行实时修正，将机器人位置精度提高到±0.2 mm、姿态精度提高到±0.1°。

图8 常见视觉伺服结构框图Fig.8 Common methods of visual servoing

反馈技术理论上可以达到很高的控制精度，但由于国外机器人控制器对外不开放，我国研究人员通常只能在国外机器人线性控制器封闭的前提下开展外部闭环控制研究。从上述分析可以看出，在目前主流的机器人精度控制方法中，离线标定和基于外部测量设备反馈的精度提高方法，几乎都是在封闭的线性控制器基础上开展的外部校准方案，难以满足不确定非线性机器人系统的高性能运动控制要求。

为了进一步提升机器人运动精度，解决机器人非线性时变和多源不确定性扰动问题，研究人员开始基于开放的控制器研究更为精细的非线性控制算法，如自适应控制、鲁棒控制、模糊控制、神经网络控制等。自适应控制本质上是从误差反馈模型提取状态信息，通过自适应算法调节控制律参数，以实现对系统的时变补偿。但是较小误差意味着系统有效信息量不足，而较大误差存在较大信息滞后，难以保证高性能动态响应，因此具有一定局限性。自适应控制对受控对象学习性强，但无法保证其动态响应速度；鲁棒控制对受控对象响应快，主要解决控制过程扰动问题，但是具有保守性，跟踪误差的渐进收敛较难。为此，文献[110-111]结合两者优点提出鲁棒自适应控制方法。但是，鲁棒自适应控制算法仍是基于系统反馈状态，估计系统特性进行运动控制，由于初始阶段无法提前获取足够的系统状态信息，易导致大的控制滞后，引起大的跟踪误差。模糊控制和神经网络控制的基本思想是设计自适应控制规律，逐渐调整模型参数，补偿系统的不确定性；或通过估计并补偿机器人动力学模型中的不确定性，以此消除或减弱其对机器人控制系统的影响。上述先进控制算法虽能一定程度改善机器人控制性能，但都由于结构和算法复杂在工程上应用具有一定难度。更主要的是，这些方法都不同程度地简化了机器人多体系统动力学模型，在简化动力学模型基础上设计的控制器势必会因难以准确预测系统动力学规律而影响控制精度。

综上分析，现有提高机器人精度的方案，要么是在标准工业机器人内部线性控制基础上开展的离线误差标定方案和基于外部测量设备的在线补偿方案，要么是在开放的控制器基础上设计复杂先进控制算法进行在线控制的方案，因无法真正意义上描述机器人实际动态特性而具有一定局限性。因此，深入研究复杂多体动力学的控制问题，提出可以补偿机器人系统非线性和不确定性因素综合影响的精确鲁棒控制策略，对实现机器人高性能和高精度运动至关重要。

3 机器人精度补偿技术的应用进展

以上研究表明，现有机器人精度补偿技术已经取得了较好的研究进展，部分研究成果已经在制孔、铣削、磨削、装配等领域开展了应用验证。

3.1 制孔铆接

传统手工制孔以风钻钻孔为主，存在孔位精度低、加工工序长、加工质量控制困难等缺点。以航空件制造为例，其存在大量的制孔工作，制孔加工的质量和效率直接影响飞机的质量和可靠性。以工业机器人为平台的自动化制孔装备是实现高质量、高效率、高柔性制孔的必然选择，因此工业机器人的定位精度成为机器人制孔亟需解决的问题。

国外已经有多家企业将基于工业机器人的钻铆系统应用于飞机制造当中，比如飞机蒙皮、翼面、方向舵等装配任务。美国EI公司与德国的宝捷公司最早开始研究工业机器人钻铆设备并将其应用于实际生产制造。美国EI公司在机器人六关节分别安装光栅尺，采用半闭环方法提升了工业机器人定位精度，并将该机器人应用到钻铆系统中，成功研发了多系列的工业机器人钻铆系统，如图9(a)所示。德国宝捷公司研发了一套机器人自动钻铆装备—RACE(Robot Assembly Cell)系统，如图9(b)所示，该系统集成了工业机器人和末端制孔系统，同时还设立了送钉系统和末端导轨，并在机器人控制软件中集成了非运动学标定精度补偿程序。

图9 高精度机器人自动钻铆系统Fig.9 High-accuracy robotic automatic drilling and riveting system

南京航空航天大学田威教授团队首次提出了误差相似度理论，并结合神经网络技术应用在机器人钻孔当中。如图10所示，该非运动学标定方法已在KUKA KR500-3机器人自动装配系统上得到验证，补偿后，机器人的位置精度和姿态精度分别提高了83.99%和54.88%，达到0.244 mm和0.037°，可以满足制孔的精度要求。该团队提出的基于非运动学标定的精度补偿技术已经在如图10(d)所示的双机器人协同钻铆系统中实现应用。

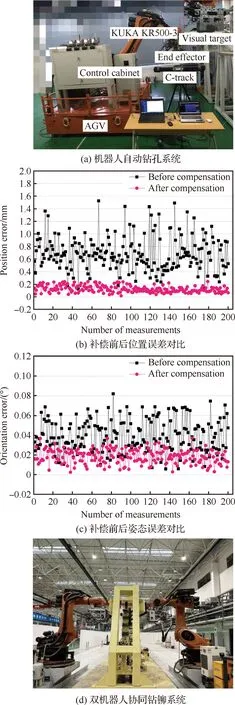
图10 基于非运动学标定的机器人自动钻铆[117]Fig.10 Robotic drilling and riveting based on non-kinematic calibration[117]

此外，机器人镗削飞机交点孔是航空叠层构件机器人制孔的典型应用。在交点孔精加工中，传统的专用数控机床虽然可以保证交点孔的加工精度和质量，但是成本较高、占地面积大、柔性差。针对这种情况，工业机器人以其机动、灵活的特点，能够安全的避开现场工装到达加工位置，然后配以镗孔末端执行器，可以完成镗孔精加工。然而机器人定位精度差、机械刚度低、极易变形和振动等问题严重影响到交点孔的加工质量。为了提高交点孔的质量和精度，浙江大学柯映林教授团队对机器人的位姿优化和精度补偿技术展开研究，如图11所示，在机器人镗孔系统的实际应用中，机器人精度得到了有效提高，交叉孔表面粗糙度达到Ra0.8级，机器人末端的位置精度为0.05 mm，姿态精度为0.05°，该方法保证了交叉孔的镗孔质量和位姿精度。

图11 基于激光跟踪仪反馈的机器人镗孔补偿对比[120]Fig.11 Comparison of robotic boring compensation before and after using laser tracker feedback[120]

3.2 铣 削

工业机器人在铣削性能等方面较数控机床设备存在很大不足，造成机器人铣削加工后的产品质量还达不到高精度要求，只能应用在产品精度要求较低的场合。目前许多国内外研究人员将精度补偿技术应用在机器人铣削上，取得不错的应用效果。

图12(a)所示是德国的弗劳恩霍夫协会研发的移动铣削机器人系统，机器人本体使用的是MABI Max MR-150，控制系统采用西门子840Dsl数控系统。这套移动机器人铣削系统结合关节转角反馈控制技术与视觉伺服控制技术，可以将机器人的定位精度提高到0.19 mm，重复定位精度提高到0.06 mm，在机器人末端进给速度3000 mm/min时，机器人轨迹精度提高到0.35 mm，轨迹重复性为0.063 mm。图12(b)所示为该团队基于激光跟踪仪闭环反馈的补偿策略与补偿效果图，工控机根据激光跟踪仪测量的实际位姿和机器人控制器接收到的目标位姿，计算出轴角修正值，最后反馈给机器人控制器，补偿后机器人定位精度由1.5 mm降低到0.13 mm。

图12 弗劳恩霍夫协会机器人铣削系统Fig.12 Robotic milling system of Fraunhofer IFAM

如图13所示，国内南京航空航天大学田威教授团队为提高工业机器人的加工精度，搭建了基于西门子840Dsl数控系统的机器人铣削系统，提出了关节空间-笛卡尔空间分级精度补偿方法。静载试验结果表明，机器人的重复定位精度由0.154 mm 提高到0.039 mm，提高了74.68%；定位精度由1.307 mm提高到0.156 mm，提高了88.06%；轨迹精度由1.346 mm提高到0.181 mm，提高了86.55%，实现了点位与轨迹精度的在线实时补偿。铣削试验结果表明，复合材料舱段铣削精度达到0.22 mm，表面粗糙度优于Ra4.8，机器人铣削系统能够满足航空航天零部件的加工精度要求。

图13 基于关节反馈与空间插值补偿的机器人铣削[124]Fig.13 Robotic milling based on joint feedback and spatial interpolation compensation[124]

3.3 磨 削

高端精密磨削任务的精度要求严苛，这对于传统制造业提出了更加严峻的挑战。例如，目前航空发动机叶片的磨削大多采用人工方法，效率低，劳动强度大且磨削的碎片对工人的健康有害。相比之下，机器人磨削是一种很有前途的自由曲面自动化加工技术。磨削任务中，机器人不仅需要与工件表面恒定压力接触，还需要机器人末端工具处于正确的初始位置，这就需要高精度的标定技术，使机器人的磨削系统在提高加工效率的同时具有更高加工质量。华中科技大学丁汉院士团队将运动学标定技术应用在机器人磨削系统当中，由于运动误差和关节刚度是影响加工质量的两个重要因素，该团队结合系统的误差补偿、工件位置优化和刀位优化方法来减少加工误差。图14为该团队的机器人磨削系统以及圆柱研磨补偿前后的对比，图14(b)中左图为设计模型，圆柱形工件未补偿前磨削平均误差达到0.151 mm，右图两个圆柱形工件补偿后平均误差降低至-0.075 mm。该方法有助于推动机器人带式磨削在对加工质量要求较高的工件上的应用。

图14 基于运动学与关节刚度补偿的机器人磨削[127]Fig.14 Robotic grinding based on kinematic and joint stiffness compensation[127]

3.4 装 配

机器人的不断发展，为装配领域走向智能化带来了契机。机器人装配广泛应用在汽车制造、电子电路、航空制造领域。然而不同于传统的机器人固定流水线装配，以飞机零部件、电子制造、星载设备等为例的装配过程对机器人的精度提出了更高要求。

此外，在电子制造过程中，装配环节具有工艺繁琐、精度要求较高、工件小、种类多等特点，湖南大学的马聪基于视觉引导设计了一套电子装配机器人，提升了电子装配精度的同时装配成功率高于99.67%。北京航空航天大学机器人研究所提出如图15所示的一种基于机器人视觉引导的星载设备智能装配方法，采用机器学习与双目视觉实现装配体之间的精确位置测量。整个装配过程可自动完成，装配时间缩短在若干分钟以内，最终应用在卫星与星载设备的模型装配试验中，结果表明装配误差小于0.3 mm。

图15 基于视觉引导的星载装配[130]Fig.15 Satellite assembly based on visual guidance[130]

4 机器人精度补偿技术发展趋势

近年来随着机器人在高端制造领域的应用逐渐深入，一些精度补偿技术的不足也开始呈现出来，例如精度补偿实时性较差、效率低下、动态精度不稳定、补偿成本高、补偿技术通用性差以及无法从根本上提升机器人精度等等问题日渐突出。

因此，为了未来机器人更好地适应单件、小批生产模式下多变的任务需求、复杂的场地环境，推动机器人在高精度制造领域的发展，本文提出以下几个未来机器人精度补偿的发展趋势。

1) 高实时性机器人精度补偿技术

随着机器人应用的增加和对自主性要求的提高，机器人精度补偿的实时性有了更高的要求。神经网络作为一种智能方法，不仅能以任意精度逼近任意连续非线性函数，而且具有较强的独立学习能力，为网络自适应重构提供了方便。视觉作为一种简单的测量方式，可以很容易地实现机器人运动时末端位姿的测量，同时也体现了机器人的高度自治性。随着神经网络收敛效率和视觉测量系统精度的提高，该组合在自主性和实时性方面显示出相当大的优势，将成为未来机器人精度补偿方向的研究热点。

2) 灵巧性与智能化机器人精度补偿技术

机器人通常在复杂、隐蔽的产品空间内部进行作业，比如飞机壁板内部的监测、标准件紧固及密封，以及进气道的测量、安装、喷涂、检验等，场地的限制往往影响到传统精度补偿方法的实施，研制出灵活适应于各种复杂环境的精度补偿方法具有良好的应用前景。为进一步降低精度补偿过程对人工的依赖，体现机器人的高度自治性，研究环境感知、信息获取、智能软件与人机交互等技术，采用可以动态实时感知、测量、捕获和传递信息及反馈控制的新技术、新方法和新流程，使机器人精度补偿各个层面的工作协同更密切，对环境、目标等信息的获取和处理更智能，在多传感器信息融合的基础上，实现补偿过程的智能化。

3) 多机协同机器人精度补偿技术

多机器人的操作精度决定了其执行协同作业任务的能力，也直接影响其应用的深度和广度，然而多机器人操作系统中灵活多变的协作形式，制约了其向自主化、智能化和高精度化方向发展。但是对比单个机器人，多机系统具有典型的分布特性，机器人之间相互取长补短，增加了功能的冗余性、系统的容错性以及组织结构的灵活性，具有单机器人无法比拟的优势，因此，机器人精度补偿向着多机协同方向发展是未来精度补偿领域的一大趋势。

4) 高鲁棒性机器人精度补偿技术

工业机器人在作业过程中通常面临不确定性扰动，如制孔、铣削过程的切削力，装配过程的干涉碰撞等，均会对其负载产生不确定性变化，最终导致机器人定位精度与轨迹精度下降。现有精度补偿技术仅对机器人受确定性载荷下的误差进行分析并施加前馈补偿，或依赖外部测量设备对机器人误差进行实时补偿，对不确定性扰动缺乏鲁棒性。研究机器人精度在受外界扰动下的变化规律，并提高精度补偿技术在不同环境、变负载作用下的鲁棒性，是进一步提高工业机器人在航空航天高端制造业应用前景的重要方向。