潜水位气压效应的消除及消除效果评价

史昊鑫, 郭 健, 曲晨豪, 葛建宏

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室, 四川 成都 610059)

地下水位一方面在某种程度上反映了岩石岩层的应力应变状态,另一方面反映了地下含水层中水量的变化,因此,地下水位的计量常常是研究地下结构构造和地下水流动模式的基础[1].潜水位受气压效应的影响较大[2],如果不能有效地消除气压效应的影响去正确计量水位,将有可能错误判断岩石岩层的应力应变状态,在地下水位比较平缓的广阔平原区,还容易错误判断区域地下水水力梯度的大小和方向[3].另外,在专门的水文地质试验中,要精确获取关键水文地质参数,往往也需要精准地监测地下水位数据[4].

国内外学者采用不同地区的水位和气压观测资料对水位的气压效应进行了研究.Bredehoeft[5]最早开始研究各种要素对井水位变化的影响,并利用滤波方法和线性回归方法来消除降雨和气压对井水位变化的影响;Roeloffs[6]通过分析承压含水层的气压效应,运用最小二乘法线性回归消除了气压对水位的影响;而Rojstaczer[7]通过研究指出,气压对水位的影响与气压的频率有关;Matsumoto等[8]利用状态空间模型并结合滤波方法,消除了固体潮、气压、降雨对井水位的影响.Toll等[9]提出使用BETCO软件程序消除气压和固体潮对水位的干扰,这为地下水观测数据的处理开辟了广阔的前景;晏锐等[10]运用小波分析法将气压数据分解为不同频段的时间序列,用最小二乘法求出气压响应系数,消除了气压对水位的影响;朱常坤等[11]利用连续小波变换对潜水位、气压进行多时间尺度分析,运用连续小波逆变换重构了气压和水位时间序列,然后用最小二乘法求出了气压效率,消除了气压对水位的影响.

以往对气压效应的研究主要集中在深层承压含水层中,而在非承压的潜水含水层中,少有气压效应影响消除的研究.为此,本文依据四川省中江县垮梁子乡一地下水监测系统中得到的高精度、高频率特征数据,首先用斜率法和Clark法两种方法求取气压效率,再通过线性回归法和反卷积法得到消除气压效应后的校正水位,最后利用频谱分析法来评价校正效果,旨在找到消除潜水含水层井水位气压效应的最佳方法.

1 数据来源与理论方法

1.1 数据来源监测井位于四川省中江县垮梁子乡的小山丘上,位置坐标为30°38′56″N、104°53′53″E.井口高程为528 m,水位埋深在21 m左右.井的水位监测设备为Micron’s Model MP102通气式传感器.地下水位数据的采集时间间隔设置为1 h,水位数据精度为1 mm,选取2018年8月25日至2019日2月18日时间段内共计3 216个井水位监测数据进行研究,得到井水位的变化曲线如图1所示.

图1 监测井水位变化曲线

同时选取Baro-Diver气压计,对研究区内大气压强进行实时监测,气压数据采集的时间间隔设置为1 h,精度约等于0.98 Pa.选取与水位监测数据相同时间段(2018年8月25日至2019年2月18日)的气压值并绘制曲线如图2.

图2 气压值变化曲线图

该时间段的气压整体呈现上升趋势.气压每小时变化最大值为411.879 3 Pa,小时变化的平均值为58.839 9 Pa;整个时间段的周变化量的最大值超过了1 961.33 Pa.

1.2 气压效应的响应原理潜水含水层的井水位受气压变化的影响,原因是大气压的变化传递到潜水面之前,空气必须进入或离开上覆包气带.这个过程会受到非饱和带的渗透性大小及其储存或释放土壤气体能力大小限制,从而导致传递压力过程变缓.因此,非饱和带土壤里气体压强的变化会滞后于地面上的气压变化.这个滞后时间取决于含水层的性质(气体渗透率、储存率)以及现有的井况(井筒储存和井壁薄壁效应).总之,造成滞后的关键因素是空气通过包气带的气动扩散系数和包气带的厚度[12].

然而,井中水位对气压变化的响应是瞬时的,导致井水和邻近含水层中的水之间的压力不平衡,这种压力差使得井中水位发生波动.这个现象可以理解为作用到井水的气压要大于作用在潜水面的气压,如图3.

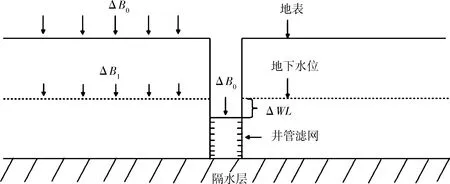
图3 潜水含水层气压效应示意图

地面上大气压压强变化了ΔB0不久后,只有其中的一部分ΔBt通过包气带传到了潜水面,然而直接作用到井水面的压强并未减小.因此,井水和含水层中的水之间会产生暂时的压力不平衡,导致井水位下降,水位的值ΔWL等于ΔB0-ΔBt.最后,整个大气压强的变化会通过包气带逐渐作用到潜水面,即差值ΔWL会随着时间逐渐消失,井水位慢慢恢复到与潜水面水位相同的位置[13].

1.3 气压效率的确定方法气压效率(Barometric Efficiency)的定义[9]可以由一个等式表示：

(1)

其中,ΔWb表示由于气压变化ΔB引起的那部分水位变化值,α为气压效率,无量纲.

气压效率表征了井水位变化对气压变化响应的敏感程度,其值为负,数值大小介于-1～0之间,确定气压效率的方法有斜率法和Clark法等.

1.3.1斜率法 斜率法是由Ferris等[14]基于多个时间间隔中的ΔW和ΔB比值提出.Y轴表示井水位的变化值ΔW,X轴表示大气压强的变化值ΔB.首先在坐标图上点绘出ΔW和ΔB,用最小二乘法求取最佳拟合线,拟合线的斜率为气压效率的估值,则气压效率

(2)

其中

S

(3)

S

(4)

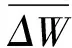
该方法存在的误差,就是用ΔW代替了ΔWi,即忽略了其他因素(除气压以外)对水位变化造成的影响,误差

εslope

(5)

其中

S

计算气压效率的误差就是i时刻的非气压引起的水位变幅ΔWi与气压变幅ΔB之间的斜率,随着采样点的规模越大,产生这种误差的可能性就越小.

1.3.2Clark方法 Clark方法是假设ΔWi不变,即假设井水位变化对除气压以外的影响因素来说是恒定的,计算气压效率的方法,要求水位数据采样时间间隔的长度是恒定的[15].

该方法比较每个时间间隔上ΔW和ΔB的正负号,并计算

∑ΔWj=∑ΔWj-1+ωj,

(7)

其中,∑ΔWj表示第j个时间间隔后水位变化的和,∑ΔWj-1表示第j-1个时间间隔后水位变化的和,ωj表示如果第j个时间段内,气压变化Bj的符号和水位变化Wj的符号相同(即在某个特殊的情况下,当气压升高时,水位值也在升高;当气压下降时,水位值也在下降),则ωj的值就取水位变化值Wj的绝对值;如果两者的符号相反,ωj的值将取水位变化值Wj的绝对值的负值.

如果Bj=0,则忽略Wj,这样就避免了非气压效应引起的水位变化叠加,减小了计算误差.

计算气压变化的原则是每个时间间隔的气压变化值的绝对值都会加到前一个时间间隔上去：

∑ΔBj=∑ΔBj-1+|ΔBj|,

(8)

那么气压效率的值就可以表示为

(9)

1.4 气压效应的消除方法

1.4.1线性回归法 通过井水位数据与气压数据的相关性分析,通过最小二乘法得到回归方程：Y=aX+b,Y表示水位埋深(m);X表示气压;a、b均为常数,其中a为气压效率α[16].

应用下式消除井水位中的气压影响成分,得到校正水位

(10)

1.4.2反卷积回归法 在考虑气压效应滞后性的情况下,Rasmussen等[3]采用反卷积回归法,利用水位-气压观测值来估计气压响应函数,并通过响应函数计算修正水头.该方法因为体现了气压效应的瞬时性特征,计算结果有较好的稳定性[17],故优于用一个气压效应常数去除气压扰动的效果.

Box等[18]建立了一套线性方程组估计气压响应函数

ΔW(t)=α(0)ΔB(t)+

α(1)ΔB(t-1)+α(2)ΔB(t-2)+…+

α(m)ΔB(t-m),

(11)

即

(12)

其中,ΔW(t)、ΔB(t)表示t时刻水位和气压的变化值,ΔB(t-i)表示t-1时刻气压的变化值,α(i)表示滞后i时的单位响应系数,m表示最大滞后时间.

对于瞬时响应,(11)式中只需保留第一项,其余全为0.通常来说,由于储层效应、井壁效应、含水层覆盖层效应以及气压变化与观测水位响应之间的延迟等原因,气压响应函数存在多个滞后项.应将滞后的最大值设置为足够大的数字,以便包括所有滞后响应.利用最小二乘线性回归求出单位响应系数α.一旦找到α(j)的值,则通过对单位响应系数求和计算阶跃式气压响应系数

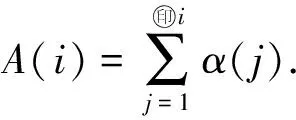
(13)

阶跃气压响应函数用于判断含水层类型(承压或非承压),如图4[9].

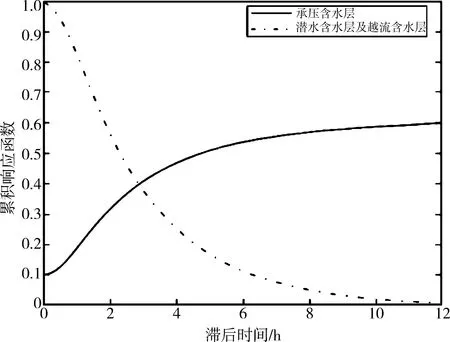
图4 承压和非承压含水层的阶跃响应函数

利用响应函数,计算每个观测值的修正值[9]：

2 气压效应消除结果

2.1 气压效率求取根据线性回归法原理,气压效率是线性回归法消除气压效应的重要参数.因此分别用斜率法和Clark法对气压效率进行求取,结果见表1.

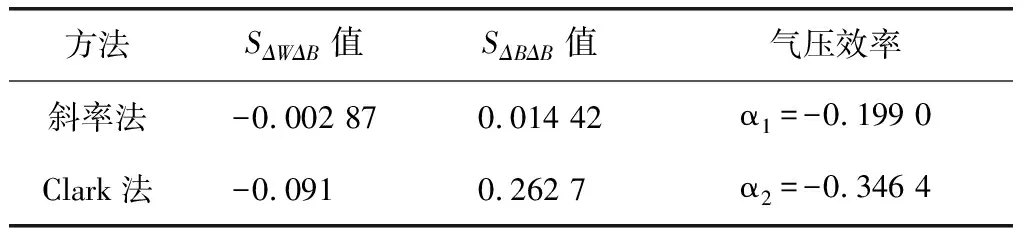
表 1 井水位气压效率计算

根据结果可见,两种方法确定的气压效率存在差异,Clark法得到的气压效率约为斜率法的1.7倍,哪个参数更准确?需要通过气压效应的消除效果来判断.

2.2 气压效应消除

2.2.1线性回归法消除 将斜率法获得的气压效率α1=-0.199 0和Clark法获得的气压效率α2=-0.346 4分别代入线性回归(10)式对井水位数据进行校正计算.由于气压变化幅度以及气压效率值都比较小,使得在长时域内校正前后的水位变化不明显,因此,选取某一周的原始水位与校正后的水位进行对比(图5),由图5可以看出,采用斜率法得到的气压效率消除气压效应的效果不明显,用Clark法得到的气压效率进行气压效应消除后,水位有明显的校正.

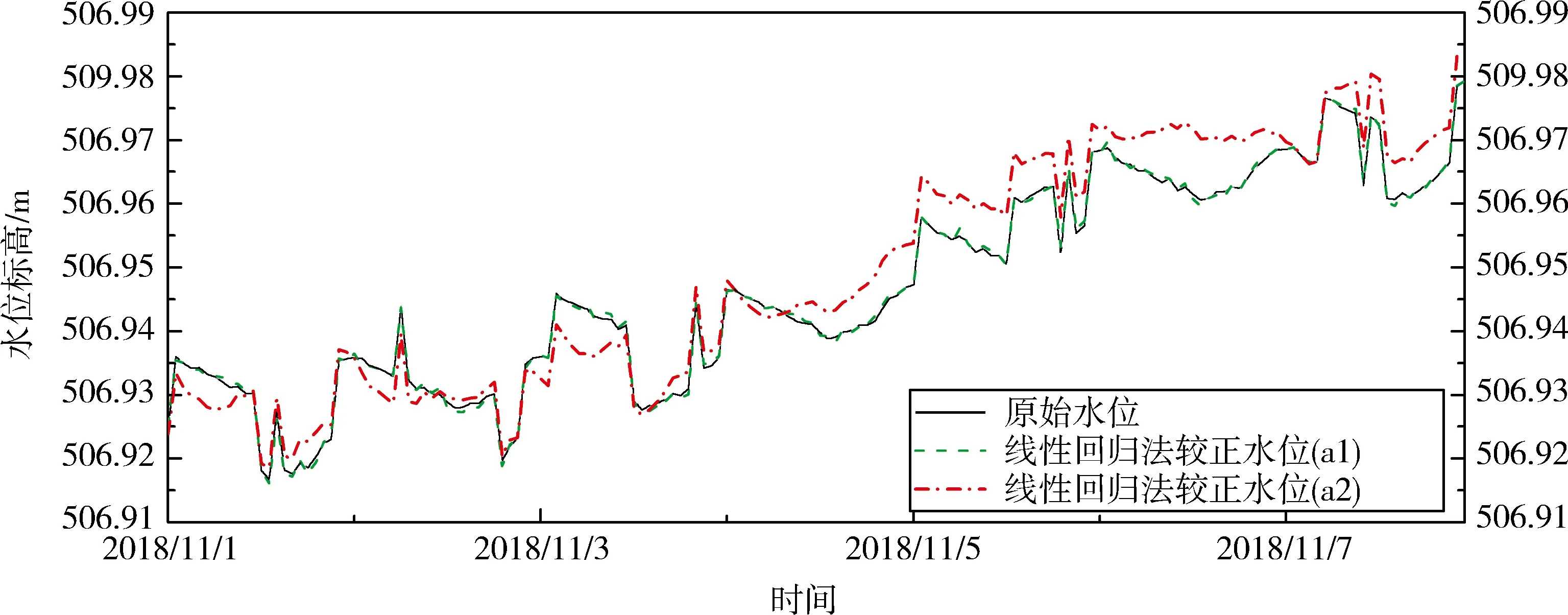
图5 线性回归法消除气压效应前后水位对比图

2.2.2反卷积回归法消除 将滞后时间的最大值m设为24 h,通过多元线性回归,求得每个水位变化ΔW(t)与不同滞后时间的气压变化ΔB(t-i)之间的线性关系,得到每个滞后时间i的ΔB前的单位响应系数值.

再根据(13)式,得到两个监测端水位滞后时间1～24 h的阶跃气压响应系数A(i);根据绘制出的气压响应函数(图6),可见函数后半段具有典型的非承压含水层特征.

图6 气压响应函数

最后,根据(14)式,求得每个时间对应水位的校正值,得到校正后的水位.同样选取某一周的时间对校正前后的水位进行对比,如图7所示.

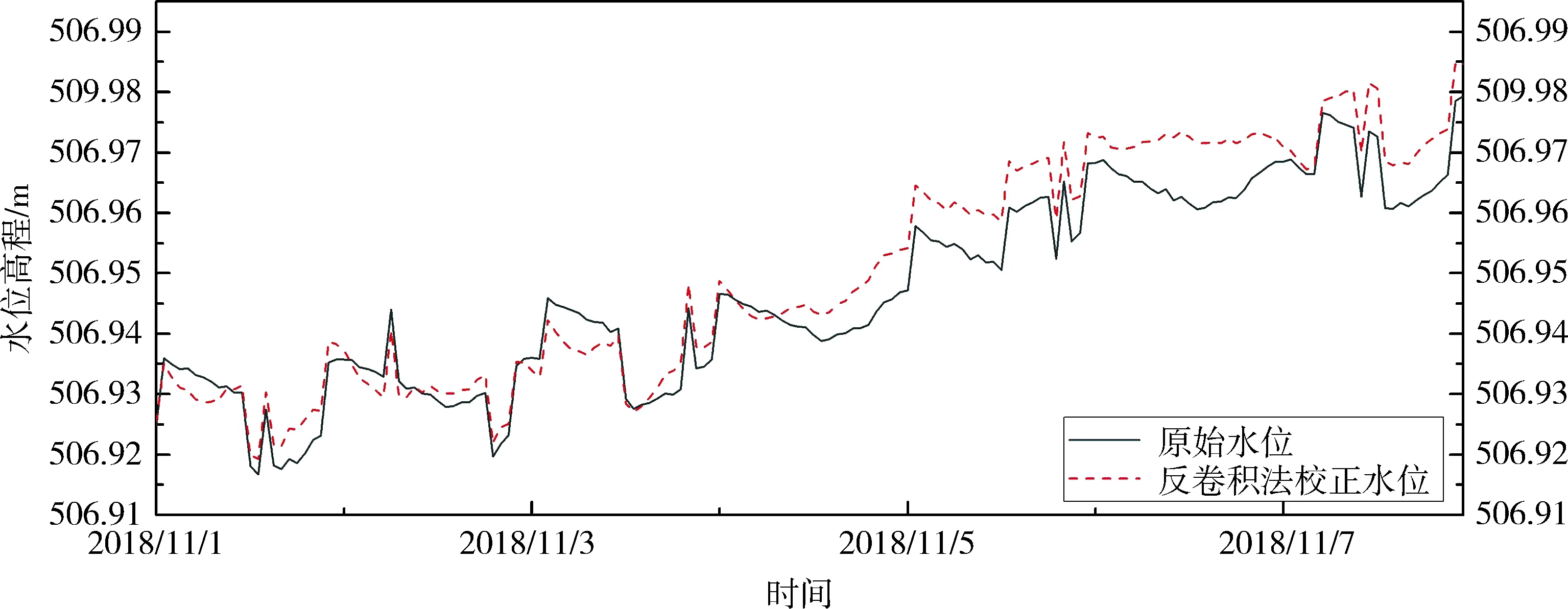
图7 反卷积回归法校正前后水位对比

从消除气压效应后的水位变化来看,反卷积回归法的消除幅度更大.此种差异产生的原因在于,反卷积回归考虑了气压效应的滞后性,而线性回归法只消除了对应时刻的气压影响.

3 讨论

由于井水位变化与气压变化存在相似的周期性,即1/3日、半日和1日周期性(图8(a)).文中采用快速傅里叶变换分别对校正前后的水位进行频谱变换,并与气压频谱和原始水位频谱进行对比,可通过观察两者的频谱图,比较水位与气压在相同波峰处的峰值是否减小或者消除,由此评价和判断气压效应的消除效果.若相应频率上的峰值减小的程度或消除的数量越多,证明井水位气压效应的消除效果越明显;反之,则气压效应的消除效果就相对较差.

用斜率法与Clark法计算出的气压效率值在数值上有较大差异,通过线性回归法计算出了两种气压效率下的校正水位,从校正后的水位数据来看,两种方法均对气压效应进行了一定程度消除.从得到两者校正水位后的频谱图(图8)中看出,斜率法与Clark法在1、3 c/d(circle per day,日循环次数)处没有有效消除掉气压效应的影响,而在2 c/d周期处均对水位中气压效应进行了削弱,从消除程度上看,Clark消除效果更好,这是因为Clark法考虑了其他因素的影响.

由图8(b)所示,利用线性回归法消除气压效应后,井水位仅在2 c/d处的峰值得到了削弱.经过反卷积法消除气压效应后,孔井水位在1、2与3 c/d处的水位峰值均得到了削弱,且在2 c/d处,即半日周期的峰值削弱得最为明显.

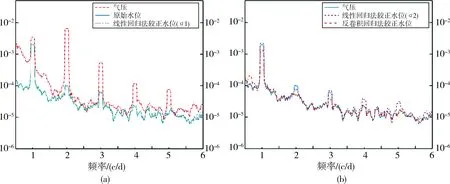
图8 水位改正前后对比频谱图

通过对比反卷积法与线性回归法处理后的井水位值和水位频谱图波峰消除幅度,可以发现反卷积法消除气压效应对地下水水位的影响优于线性回归法.其原因在于反卷积回归法考虑了前24 h的气压变化影响,而线性回归法并未考虑气压效应的滞后性.

此外,在频谱图8中1 c/d处,即1日周期的峰值消除效果并不明显.分析原因可能在于影响地下水微动态变化的外界因素不止气压效应,植物的蒸腾作用以及固体潮等亦对地下水位产生影响,由于植物蒸腾作用和固体潮作用都存在明显的1 d周期,所以有可能是植物蒸腾作用和固体潮作用对井水位变化产生的影响.

4 结论

基于垮梁子一潜水含水层中的监测井,讨论气压效率求取和气压效应消除的不同方法,得出如下结论：

1) 用线性回归法对气压效应进行消除,分别采用斜率法和Clark法求取气压效率,从频谱分析结果来看,Clark法获取的气压效率比斜率法更可靠.

2) 用线性回归法和反卷积回归法对潜层含水层井水位进行气压效应消除,从消除效果来看,反卷积回归法很好地削弱了井水位1/3、1/2和1 d波峰,而线性回归只能消除部分的1/2 d波峰,反卷积回归法优于线性回归法.