随机系统的Fuzzy系统逼近
2022-07-01李洪兴
李洪兴
(1. 北京师范大学珠海校区 应用数学学院, 广东 珠海 519085; 2. 大连理工大学 控制科学与工程学院, 辽宁 大连 116024)
1 随机系统产生的背景
考察图1所示的单输入单输出开环系统S,输入变量x在输入论域X中取值,输出变量y在输出论域Y中取值.如果该系统S是个确定性系统,可以采用常规方法建立系统S的数学模型(如用机理建模法建立微分方程模型),再用解析方法或数值方法获得该模型的解y(x),这样则认为已经掌握了该系统.这时该系统S可以简单地理解为一个函数关系,记为s,即
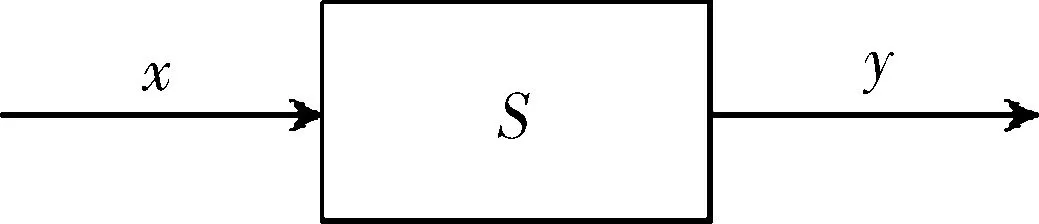
图1 单输入单输出开环系统
s:X→Y,xy≜s(x).
(1)
这样,可以将该系统形式化地记为s=S(X,Y).
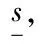
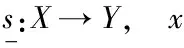
(2)
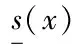
用随机的观点看上述问题有这样的含义,在X中随机抽取一点x丢入系统S的输入通道,进入系统后,在系统的输出通道应有一个输出y(x)与之对应,但y(x)在Y中取哪一个元素无法预先知道,这意味着对该系统S来说存在两个随机变量ξ和η,它们分别定义在概率空间(X,B1,P1)和(Y,B2,P2)上,其中B1和B2分别为X与Y上的Borelσ-域,P1和P2分别为B1和B2上的概率测度.
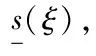
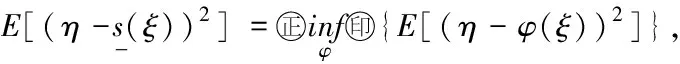
其中φ取自一类Borel可测函数空间.熟知,条件数学期望即可满足此要求[1],即应置

(4)
注 1.1根据(4)式,要证(3)式当且仅当证明:对于上述任何Borel可测函数φ,均有
事实上,
E[(η-φ(ξ))2]=
E{[(η-E(η|ξ))+(E(η|ξ)-φ(ξ))]2}=
E[(η-E(η|ξ))2]+E[(E(η|ξ)-φ(ξ))2]+
2E[(η-E(η|ξ))(E(η|ξ)-φ(ξ))].
显然有E[(η-E(η|ξ))(E(η|ξ)-φ(ξ))]=0,从而
E[(η-φ(ξ))2]=
E[(η-E(η|ξ))2]+E[(E(η|ξ)-φ(ξ))2]≥
ξ:Ω→R, (x,y)ξ(x,y)≜ξ(x),
η:Ω→R, (x,y)η(x,y)≜η(y),
这样,(ξ,η)便成为联合概率空间(Ω,F,P)上的二维随机向量.这时,任取x∈X,当ω∈{ω∈Ω|ξ=x}时有
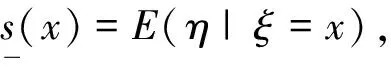
(5)

如果掌握(ξ,η)的全部概率信息,特别能知道(ξ,η)的概率密度f(x,y),则(5)式从形式上变为具体可操作的计算式

(6)
这里自然要求∀x∈X,满足条件


显然在实际计算中,(6)式应为
(7)
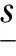
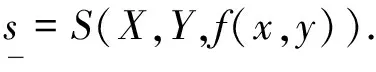
(8)
2 单输入单输出连续随机系统的Fuzzy推理意义
为了方便,须明确几个概念.给定某个论域X,A={Ai|1≤i≤n}为X上的一族正规Fuzzy集,即∀i∈{1,2,…,n},有∃xi∈X使得μAi(xi)=1,其中xi叫做Ai的峰点;当然,峰点不必唯一.A为X的一个Fuzzy划分,如果满足条件
(9)
不难验证具有这样特性的Fuzzy集满足Kronecker性质[4-6]
μAi(xj)=δ
此外,为了证明下面的主要定理,先给出3个引理.这3个引理均与含参积分有关.
引理 2.1设f(x,y)为X×Y上的二元连续函数,其中X=[a1,b1],Y=[a2,b2]均为有限实区间,对于如下的含参积分

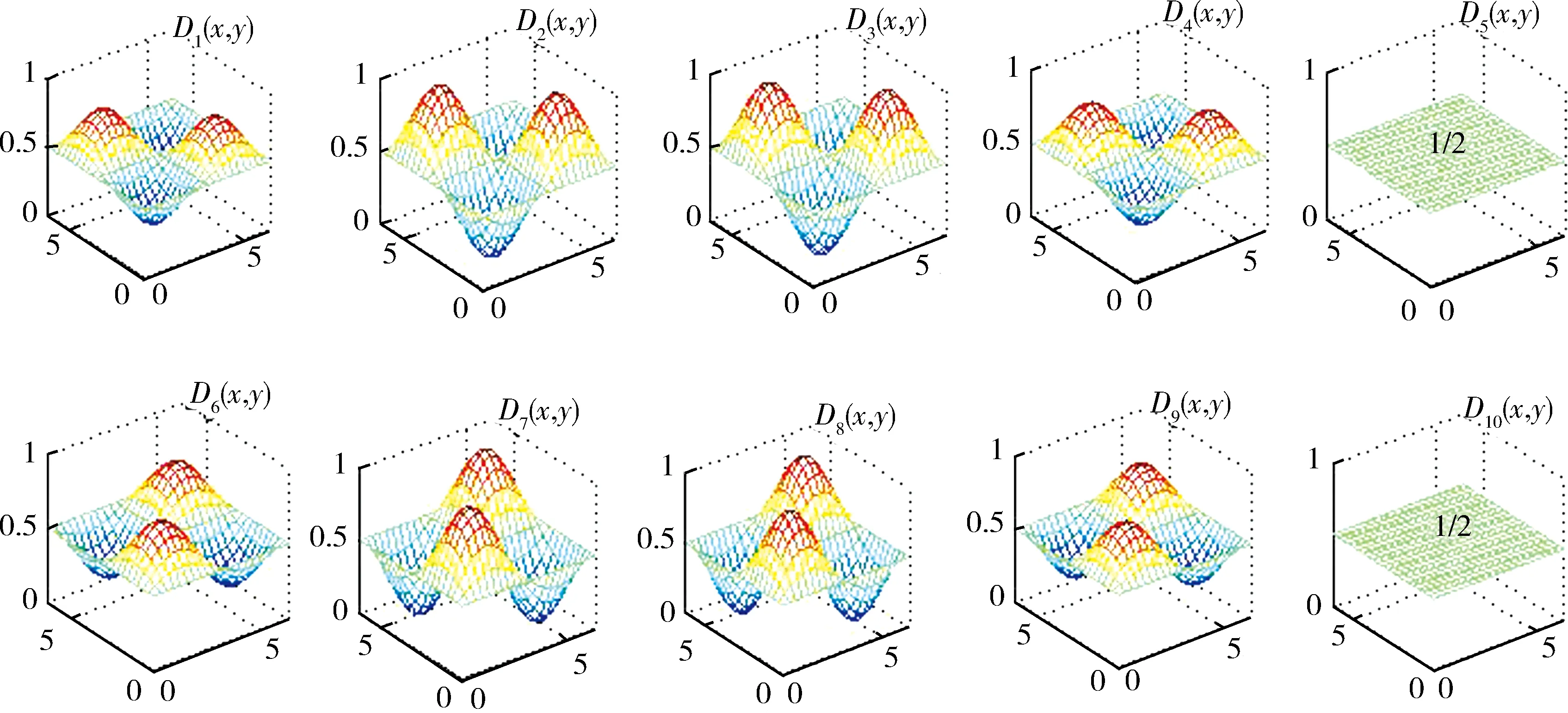
来说必有这样的结论:任意取定ε>0,总存在一个与参数x无关的公共的δ>0,使得对于Y的任意划分a2=y0 λ=max{Δyi|i=1,2,…,n}<δ, 其中 Δyi≜yi-yi-1,i=1,2,…,n, 且ξi在[yi-1,yi]中任取. 证明任意取定ε>0,令δk=1/k,k=1,2,….可证一定存在一个k使δ=δk满足该引理的结论.若不然,则对每个k,存在xk∈X,并存在Y的划分 a2=y(k)0 λk≜max{Δy(k)i|i=1,2,…,nk}<δk, 但|I(x注意{xk}为有界点列,必有收敛的子序列{xkj},使得 xkj→x*∈X,j→∞. 注意到δkj→0(j→∞),有 这是明显的矛盾,这便证明了该引理. 引理 2.2设f(x,y)为X×Y上的二元连续函数,其中X=[a1,b1],Y=[a2,b2]均为有限实区间,对于如下含参积分 λ=max{Δyi|i=1,2,…,n}<δ⟹ 证明首先,注意到 因此存在I(x)的最小点x0∈X,使得有 I(x)≥I(x0), ∀x∈X. 取ε=I(x0),由引理2.1知,存在δ>0,使得对于Y的任意划分 a2=y0 λ<δ⟹ 这时有 I(x0)-ε=0 对一切x∈X一致地成立,故该引理的结论为真. 根据引理2.2并采用类似引理2.1的证明方法立即可以得到下面的引理2.3. 引理 2.3设f(x,y)为X×Y上的二元连续函数,其中 X=[a1,b1],Y=[a2,b2] 均为有限实区间,满足条件 任意取定ε>0,总存在一个与参数x无关的公共的δ>0,对于Y的任意划分 a2=y0 只要λ=max{Δyi|i=1,2,…,n}<δ,则对所有x∈X一致地成立 其中Δyi≜yi-yi-1,且ξi在[yi-1,yi]中任取. 定理 2.1任意给定一个连续随机系统 其中X=[a1,b1],Y=[a2,b2]均为有限实区间.如果∀x∈X有 则存在一组Fuzzy推理规则: IfxisAi,thenyisBi,i=1,2,…,n, (10) 证明作区间Y上的划分 P:a2=y0 记γ≜(y1,y2,…,yn),以及 Δyi=yi-yi-1,i=1,2,…,n, λ=max{Δyi|i=1,2,…,n}, 于是 其中已经规定 μ (11) 根据划分P构造n+1个Y上的Fuzzy集Bj,j=0,1,…,n,要求诸Bj组成Y的一个Fuzzy划分且在Y上连续.这相当于把诸清晰点yj,j=0,1,…,n模糊化,比如Bj可取“三角波”型隶属函数[7-9](见图2): 图2 由Bj形成的一组Fuzzy 划分 μ μ j=1,2,…,n-1; μ 再构造Ai(i=1,2,…,n)如下 μAi(x)≜f(x,y (12) 置A≜{Ai|1≤i≤n},B≜{Bi|1≤i≤n},视A、B为语言变量,它们分别在自身中取值,于是可形成Fuzzy推理规则组(10)式,将按CRI算法来构造一个Fuzzy系统,过程如文献[10]. 首先由(10)式中第i条Fuzzy推理规则形成一个X×Y上的Fuzzy关系Ri≜Ai×Bi,隶属函数为 ∀(x,y)∈X×Y, μRi(x,y)=μAi(x)∧μBi(y). ∀(x,y)∈X×Y, μ 任取A∈F(X),通过R应获得Fuzzy推理结果B∈F(Y),这相当于由Fuzzy关系R诱导一个从F(X)到F(Y)的Fuzzy变换,记为“∘”,即 ∘:F(X)→F(Y),AB=∘(A)≜A∘R. 隶属函数规定为:∀y∈Y, μ (13) 对任意指定的输入x′∈X,为能使用(13)式,需将x′Fuzzy化,可以规定单点Fuzzy集A′∈F(X): μA′(x)≜χ{x′}(x). (14) 代入(13)式得到Fuzzy推理结果B′∈F(Y):∀y∈Y, μ (15) B′是个Fuzzy集,故需经清晰化方法得到确切的量y′∈Y.由(15)式易知μB′(y)在Y上分段连续,故满足条件: μ μAi0(x′)∧μBi0(y), 由此可知,μBi0(y)=0,a.e.,这与诸Bj为连续的正规Fuzzy集的规定相冲突.这样一来,可令 根据引理2.2有 ∃δ3>0,λ<δ3⟹∀x∈X, 注意(16)式的Riemann和并注意Bi满足Kronecker性质,有 (17) 其中已置 μ 从(17)式及引理2.3知∃δ4>0,使得δ4<δ3,当λ<δ4时,对所有的x∈X一致地有 这样一来可取δ=min{δ2,δ4}并注意(11)式,当λ<δ时,对所有的x∈X一致地有 注 2.1在定理的证明中,构造Fuzzy集Ai采用了(12)式.其实亦可采用下式 μAi(x)≜f(x,yi)/M,i=1,2,…,n, (18) 其中 M≜max{f(x,y)|(x,y)∈X×Y}. 这时同样可以证明该定理,证明细节从略.不过定理3.1的证明使用了这种证法. 如果取r2=0.5,a1=0,a2=0,σ1=0.5,σ2=1.5,则上式为 根据3σ原则,X与Y可近似地取为有限区间,如X按6σ1取有限区间[-3,3],Y按4σ2取有限区间[-6,6],根据定理2.1有 其图像见图3. 图3 连续随机系统的输出曲线图像 图4 Fuzzy集Bj的隶属函数 诸μAi(x)的表达式如(12)式 μ 其图像见图5. 图5 Fuzzy集Ai的隶属函数 来计算 图6 Fuzzy系统的输出曲线 图7 h=1时与的比较 y0=-6,y1=-5.5,y2=-5, …,y24=6. 图8 h=0.5时与的比较 图9 h=0.1时与的比较 考虑图10所示的双输入单输出开环系统S,输入变量x与y分别在输入论域X和Y中取值,输出变量z在输出论域Z中取值.如果该系统S是个确定性系统,可用机理建模法建立系统S的数学模型(如偏微分方程模型),再用某种方法获得解z(x,y)后,则认为掌握了该系统.这时该系统S可以理解为一个二元函数关系,仍记为s,即 图10 双输入单输出开环系统 s:X×Y→Z, (x,y)z≜s(x,y). (19) 于是该系统可记为s=S(X×Y,Z). 当S是一个不确定性系统时,虽然很难得到“准确的”函数关系(19),却常常可以设法获得一个近似的函数关系 (x,y) (20) 设X、Y、Z均为实数空间R上的可测集,ξ、η、ζ分别为定义在概率空间(X,B1,P1)、(Y,B2,P2)、(Z,B3,P3)上的随机变量,其中B1、B2、B3分别为X、Y、Z上的Borelσ-域,P1、P2、P3分别为B1、B2、B3上的概率测度,取Ω≜X×Y×Z以及 F≜B1×B2×B3,P≜P1×P2×P3, 其中F为B1、B2、B3的卡氏积生成的Borelσ-域,P为乘积概率测度.这样便得到联合概率空间(Ω,F,P).不换记号,重新把ξ、η、ζ定义为Ω上的随机变量: ξ:Ω→R, (u,v,w)ξ(u,v,w)≜ξ(u), η:Ω→R, (u,v,w)η(u,v,w)≜η(v), ζ:Ω→R, (u,v,w)ζ(u,v,w)≜ζ(w). 这样(ξ,η,ζ)便成为联合概率空间(Ω,F,P)上的三维随机向量.任取(x,y)∈X×Y,当 ω∈{ω∈Ω|ξ=x,η=y} 时,可令 (21) 假如能知道(ξ,η,ζ)的连续概率密度f(x,y,z),那么条件数学期望(21)式具体化为 (22) 这里要求∀(x,y)∈X×Y,满足 (23) 为了下面证明主要定理的需要仍要先给出两个引理. 引理 3.1设f(x,y,z)为X×Y×Z上的三元连续函数,其中,X=[a1,b1],Y=[a2,b2],Z=[a3,b3]均为有限实区间,对于含双参积分 来说必有这样的结论:任意取定ε>0,总存在一个与参数(x,y)无关的公共的δ>0,对于Z的任意划分 a3=z0 只要λ=max{Δzi|i=1,2,…,n}<δ,那么I(x,y)的Riemann和必满足条件: 对所有的(x,y)∈X×Y一致地成立,其中,Δzi≜zi-zi-1(i=1,2,…,n)且ξi在[zi-1,zi]中任取. 证明任意取定ε>0,令δk=1/k,k=1,2,…,可证一定存在一个k使δ=δk满足该引理的结论.事实上,倘若不然,则对每个k,存在(xk,yk)∈X×Y,并存在Z的划分 a3=z(k)0 |I(xk,y 注意{(xk,yk)}中{xk}为有界点列,必有收敛的子序列{xkj},使得xkj→x*∈X(j→∞).另外{ykj}也为有界点列,故也有收敛的子序列{ykjp},使得 ykjp→y*∈Y,p→∞. 注意到δkjp→0(p→∞),有 0<ε≤ 这是明显的矛盾,从而该引理的结论正确.证毕. 引理 3.2设f(x,y,z)为X×Y×Z上的三元连续函数,其中X=[a1,b1],Y=[a2,b2],Z=[a3,b3]均为有限实区间,对于含双参积分 来说,如果∀(x,y)∈X×Y有I(x,y)>0,则存在δ>0,使得对于Z的任意划分: a3=z0 λ=max{Δzi|i=1,2,…,n}<δ⟹ 其中Δzi≜zi-zi-1(i=1,2,…,n). 证明思路如同引理3.1,从略.此外,还有类似引理2.3的下述引理. 引理 3.3设f(x,y,z)为X×Y×Z上的三元连续函数,其中X=[a1,b1],Y=[a2,b2],Z=[a3,b3]均为有限实区间,满足条件 任意取定ε>0,总存在一个与参数(x,y)无关的公共的δ>0,对于Z的任意划分 a3=z0 只要λ=max{Δzi|i=1,2,…,n}<δ,便对所有(x,y)∈X×Y一致地成立 其中,Δzi=zi-zi-1,i=1,2,…,n,并且ξi在闭区间[zi-1,zi]中任取. 则存在一组Fuzzy推理规则 If(x,y)isDithenzisCi, i=1,2,…,n, (25) 证明作区间Z的一个划分: a3=z0 记Δzi≜zi-zi-1(i=1,2,…,n),以及 λ=max{Δzi|i=1,2,…,n}, 由此得到两个Riemann和: 由该定理条件及引理3.2,∃δ1>0,当λ<δ1时有 于是 其中已经定义 μDi(x,y)≜f(x,y,zi)/M, (26) 这里 M≜max{f(x,y,z)|(x,y,z)∈X×Y×Z}, μ 任意指定一个逼近精度ε>0,因f(x,y,z)连续,故由引理3.3,∃δ2>0,使得δ2<δ1,当λ<δ2时,对所有的(x,y)∈X×Y一致地有 利用分点zj(j=0,1,…,n)构造n+1个Z上的Fuzzy集Cj(j=0,1,…,n),使得它们在Z上连续且组成Fuzzy划分,比如仍可用“三角形”模糊化方法(参考图2).置 D={Di|1≤i≤n}, C={Ci|1≤i≤n}, 视D、C为语言变量,可形成Fuzzy推理规则组 If(x,y)isDithenzisCi, i=1,2,…,n. (27) μRi(x,y,z)=μDi(x,y)∧μCi(z). μ 任取D∈F(X×Y),通过R应获得Fuzzy推理结果C∈F(Z),这里C≜D∘R,即 μ 对任何(x′,y′)∈X×Y,先作 Fuzzy化 μD′(x,y)≜χ{(x′,y′)}(x,y), 再代入(28)式得推理结果C′∈F(Z), μC′(z)=μR(x′,y′,z)= 易知μC′(z)>0.令 (29) ∀(x,y)∈X×Y 及引理3.2,∃δ3>0,当λ<δ3时有 ∀(x,y)∈X×Y. 注意(29)式的Riemann和,并注意Ci满足Kronecker性质,有 μ 再由引理3.3,∃δ4>0,使得δ4<δ3,当λ<δ4时,对所有的(x,y)∈X×Y一致地有 注 3.1在定理的证明中,构造Fuzzy集Di采用了(26)式.其实亦可采用下式 μ (30) 按(30)式同样可以证明该定理,证明细节从略.不过定理2.1的证明使用了这种证法. 例 3.1给定连续随机系统 X=Y=Z=[0,2π], 根据定理3.1有下式(其图像见图11): 图11 连续随机系统的输出曲面 z0=0,z1=0.2π,z2=0.4π, …, z9=1.8π,z10=2π, 然后作Fuzzy集Ci(i=0,1,…,10),见图12. 图12 Fuzzy集Ci的隶属函数曲线 诸Di(x,y)的表达式(26)式 μ 其中M=1/4π3,Di(x,y)的图像见图13.来计算 图13 Fuzzy集Di的隶属函数曲面 图14 Fuzzy系统的输出曲面 图15 h=0.2π时的误差曲面 图16 h=0.1π时的误差曲面 图17 h=0.01π时的误差曲面 现在考虑p个输入q个输出的开环系统S,输入变量xi在输入论域Xi中取值i=1,2,…,p,输出变量yj在输出论域Yj中取值j=1,2,…,q.如果该系统S是个确定性系统,可用机理建模法建立系统S的数学模型,再用某种方法获得该模型的一组解 yj=yj(x1,x2,…,xp),j=1,2,…,q s (x1,x2,…,xp)yj≜sj(x1,x2,…,xp), (31) 再记s≜(s1,…,sq),则(31)式可以更紧凑地写为向量值函数形式 (x1,x2,…,xp)(y1,y2,…,yq)= s(x1,x2,…,xp)= (s1(x1,x2,…,xp),…,sq(x1,x2,…,xp)). (32) 于是该系统可记为 当S是一个不确定性系统时,虽然很难得到“准确的”函数关系组(31),却常常可以设法获得一个近似的函数关系组 (x1,x2,…,xp)y (33) (x1,x2,…,xp)(y1,y2,…,yq)= (34) 仍考虑用条件数学期望来实现上述逼近的思想. Ω P 这样得到q个联合概率空间 (Ωj,Fj,Pj),j=1,2,…,q. 不换记号,重新把诸ξi,i=1,2,…,p定义为每个Ωj,j=1,2,…,q上的随机变量: ξi:Ωj→R, (u1,u2,…,up,vj) ξi(u1,u2,…,up,vj)≜ξi(ui), 而把ηj只重新定义在与其具有同样指标的Ωj上: ηj:Ωj→R, (u1,u2,…,up,vj) ηj(u1,u2,…,up,vj)≜ηj(vj), 这样得到在(Ωj,Fj,Pj)上有定义的p+1维随机向量(ξ1,ξ2,…,ξp,ηj),j=1,2,…,q.任取 (x1,x2,…,x 当ωj∈{ωj∈Ωj|ξi=xi,i=1,2,…,p}时,可令 E(ηj|ξ1=x1,x2,…,ξp=xp). (35) 如果掌握了(ξ1,ξ2,…,ξp,ηj)的连续概率密度fj(ξ1,ξ2,…,ξp,ηj),j=1,2,…,q,那么条件数学期望(35)式具体化为 j=1,2,…,q. j=1,2,…,q. (37) 如果记 F(x1,x2,…,xp,y1,y2,…,yq)≜ (f1(x1,x2,…,xp,y1),…,fq(x1,x2,…,xp,yq)), 则可以把(37)式紧凑地写为向量形式 (39) 注 4.1如果取 则得到统一的联合概率空间(Ω,F,P).不换记号,重新把诸ξi,i=1,2,…,p,ηj,j=1,2,…,q定义为Ω上的随机变量 ξi:Ω→R, (u1,u2,…,up,v1,v2,…,vq) ξi(u1,u2,…,up,v1,v2,…,vq)≜ξi(ui), ηj:Ω→R, (u1,u2,…,up,v1,v2,…,vq) ηj(u1,u2,…,up,v1,v2,…,vq)≜ηj(vj). 获得在(Ω,F,P)上有定义的p+q维随机向量 (ξ1,ξ2,…,ξp,η1,η2,…,ηq). 当知道(ξ1,ξ2,…,ξp,η1,η2,…,ηq)所服从的连续概率密度f(x1,x2,…,xp,y1,y2,…,yq)时,(39)式更应记为 f1(x1,x2,…,xp,y1)= f2(x1,x2,…,xp,y2)= …, fq(x1,x2,…,xp,yq)= 即fj(x1,x2,…,xp,yj),j=1,2,…,q不过是 f(x1,x2,…,xp,y1,y2,…,yq) 的边缘概率密度.于是(40)式很容易变为(38)式,但反之不然.好在知道诸边缘概率密度fj(x1,x2,…,xp,yj),j=1,2,…,q之后对于构造连续随机逼近系统已足够了. 为了下面证明主要定理的需要仍要先给出两个类似引理3.1和引理3.2那样的引理.由于基本表述形式类似,从略. 定理 4.1任意给定一个p输入q输出连续随机系统(38),其中 Xi=[ai,bi],i=1,2,…,p, Yj=[cj,dj],j=1,2,…,q 均为有限实区间.如果满足条件: ∀(x1,x2,…,x 则存在q组Fuzzy推理规则: If(x1,x2,…,xp)isAkjj,thenyjisBkjj, kj=1,2,…,nj,j=1,2,…,q, (41) 其中, A kj=1,2,…,nj,j=1,2,…,q, 证明记Aj≜{Akjj|1≤kj≤nj}以及 Bj≜{Bkjj|1≤kj≤nj},j=1,2,…,q, 那么上述q组Fuzzy推理规则可简写为 Aj→Bj,j=1,2,…,q. 按照定理3.1的方法由Aj→Bj,j=1,2,…,q可以构造q个子Fuzzy系统 j=1,2,…,q. 它们分别能逼近q个子随机系统 j=1,2,…,q (42) Aj→Bj,j=1,2,…,q, (43) 先考虑单输入单输出不确定性系统s=S(X,Y).假定已经知道有关系统S的一些概率信息,自然应从随机的角度去考察该系统.设X、Y均为实数空间R上的可测集,输入随机变量ξ和输出随机变量η分别定义在概率空间(X,B1,P1)和(Y,B2,P2)上,其中B1和B2分别为X与Y上的Borelσ-域,P1和P2分别为B1和B2上的概率测度,如同第一节那样构造联合概率空间(Ω,F,P),于是(ξ,η)便为(Ω,F,P)上的随机向量.无妨认为掌握的概率信息就是该系统的离散型概率分布 {P(xi,yj)|1≤i≤n,1≤j≤m}, 其中X=[a1,b1],Y=[a2,b2],以及 a1≤x1 y0≜a2 它视为系统S在得到输入xi后的响应.这样,若记 注 5.1按通常的习惯,总把P(xi,yj)记为pij,即pij≜P(xi,yj),这样表达起来简便,故下面采用简便表达法. 定理 5.1任意给定一个离散随机系统 其中X=[a1,b1],Y=[a2,b2]均为有限实区间,一定存在一组Fuzzy推理规则: Δyj≜yj-yj-1,j=1,2,…,m. 证明首先考虑如何构造Fuzzy推理规则组(45)式.Fuzzy集Bj∈F(Y)最易获得,事实上只需按图2 做成“三角波”型隶属函数,只不过将下标n改为m即可.于是就得到语言变量 B={Bj|1≤j≤m}. 再来构造Fuzzy集Aj∈F(X).先按图2那样构造充当基函数用的一组Fuzzy集αi∈F(X),i=1,2,…,n: μ μ i=2,3,…,n-1; μ 用上述Fuzzy集αi(i=1,2,…,n)的加权平均来构造Fuzzy集Aj, μ j=1,2,…,m, (46) 其中权向量组{(a1j,a2j,…,anj)|1≤j≤m}待定.这样形式地得到语言变量 A={Aj|1≤j≤m}, 于是便形成了Fuzzy推理规则组(45)式: IfxisAj,thenyisBj,j=1,2,…,m. (47) 因为μAj(xi)=aij,所以 (48) 比较(44)式与(48)式,可取 aij=P(xi,yj)M/Δyj, 令 ε≜max 则最终得到 此外,任意取定精度ε>0,由(48)式知,∃δ>0,当λ<δ时,对所有xi,i=1,2,…,n有 再考虑双输入单输出不确定性系统s=S(X×Y,Z).设X、Y、Z均为实数空间R上的可测集,输入随机变量ξ、η和输出随机变量ζ分别定义在概率空间(X,B1,P1)、(Y,B2,P2)、(Z,B3,P3)上,其中B1、B2和B3分别为X、Y与Z上的Borelσ-域,P1、P2和P3分别为B1、B2和B3上的概率测度,可构造联合概率空间(Ω,F,P),于是(ξ,η,ζ)便为(Ω,F,P)上的随机向量.已知离散型概率分布 {P(xi,yj,zk)|1≤i≤n,1≤j≤m,1≤k≤p}, 其中, X=[a1,b1],Y=[a2,b2],Z=[a2,b2], 以及 a1≤x1 a2≤y1 z0≜a3 (49) (50) 定理 5.2任意给定一个离散随机系统(50),其中,X=[a1,b1],Y=[a2,b2],Z=[a2,b2]均为有限实区间,一定存在一组Fuzzy推理规则: If(x,y)isDk,thenzisCk, k=1,2,…,p, (51) ∀i∈{1,2,…,n}, ∀j∈{1,2,…,m}, 证明类似定理5.1的情况,从略. Ω P 按照连续随机系统的处理方法可构造q个联合概率空间 (Ωj,Fj,Pj),j=1,2,…,q, 使得诸ξi,i=1,2,…,p为在每个Ωj上有定义的随机变量,ηj为只在与其具有同样指标的Ωj上有定义的随机变量(j=1,2,…,q).这样便得到在(Ωj,Fj,Pj),j=1,2,…,q上有定义的p+1维随机向量(ξ1,ξ2<…,ξp,ηj),j=1,2,…,q.进一步假设 Xi=[ai,bi],i=1,2,…,p, Yj=[cj,dj],j=1,2,…,q 均为有限实数区间.已知q组离散型概率分布 {Pj(x1k1,x2k2,…,xpkp,yjlj)|1≤k1≤n1,…, 1≤kp≤np;1≤lj≤mj},j=1,2,…,q, 其中 ai≤xi1 cj≤yj1 假定∀(k1,k2,…,kp),有 记 E(ηj|ξi=xiki,i=1,2,…,n)= (52) 将它视为系统S在得到输入(x1k1,x2k2,…,xpkp)后关于输出变量yj的响应.再置 {Pj(x1k1,x2k2,…,xpkp,yjlj)}(1≤ki≤ni,i=1,2,…,p;1≤lj≤mj), j=1,2,…,q). (54) 定理 5.3任意给定一个p输入q输出离散随机系统(54),其中 Xi=[ai,bi],i=1,2,…,p, Yj=[cj,dj],j=1,2,…,q 均为有限实区间,一定存在q组Fuzzy推理规则 If(x1,x2,…,xp)isAkjj,thenyjisBkjj, kj=1,2,…,mj,j=1,2,…,q, 其中, A kj=1,2,…,mj,j=1,2,…,q, {yjlj|1≤lj≤mj},j=1,2,…,q 的分割间隔越小,逼近的精度越高. 证明类似定理5.1及定理4.1的情况,从略. 注 5.2如果取 则得到统一的联合概率空间(Ω,F,P).不换记号,重新把诸ξi(i=1,2,…,p)和ηj(j=1,2,…,q)定义为Ω上的随机变量便得到在(Ω,F,P)上有定义的p+q维随机向量 (ξ1,ξ2,…,ξp,η1,η2,…,ηq). 当知道关于该不确定性系统S的随机向量(ξ1,ξ2,…,ξp,η1,η2,…,ηq)所服从的离散概率分布 {P(x1k1,x2k2,…,xpkp,y1l1,…,xqlq)|1≤k1≤n1, 1≤k2≤n2,…,1≤kp≤np;1≤l1≤m1, 1≤l2≤m2,…,1≤lq≤mq} 时,(54)式更应记为 {P(x1k1,x2k2,…,xpkp,y1l1,y2l2,…,yqlq)}). (55) P1(x1k1,x2k2,…,xpkp,y1l1)= P2(x1k1,x2k2,…,xpkp,y2l2)= Pq(x1k1,x2k2,…,xpkp,yqlq)= 即{Pj(x1k1,x2k2,…,xpkp,yjlj)},j=1,2,…,q不过是{P(x1k1,x2k2,…,xpkp,y1l1,y2l2,…,yqlq)}的边缘概率分布.于是于是(55)式很容易变为(54)式. 以单输入单输出开环系统s=S(X,Y)为例来讨论Fuzzy系统与随机系统转换中的还原性问题,暂限于连续系统,至于离散系统的讨论是其特例,处理起来并不困难,这里X=[a1,b1],Y=[a2,b2]均为有限实区间. 先假定已知一个Fuzzy系统 其中A={Ai|1≤i≤n}和B={Bi|1≤i≤n}分别为X与Y上的Fuzzy划分,视A与B为语言变量便可构成一组Fuzzy推理规则 IfxisAi,thenyisBi,i=1,2,…,n. 为了方便将这样的Fuzzy推理规则组简记为 A→B, (56) 其中θ为Fuzzy蕴涵算子,满足条件 θ(a,1)=a,θ(a,0)=0, ∀a,b∈[0,1].(58) 再根据文献[1],存在一个联合概率空间(Ω,F,P),其中 Ω=X×Y, F=F1×F2,P=P1×P2, 随机变量ξ与η分别定义在概率空间(X,F1,P1) 和 (Y,F2,P2)中;经过将ξ与η重新定义在概率空间(Ω,F,P)后得到随机向量(ξ,η),它服从由下列概率密度确定的概率分布 H(2,n,θ,∨)= (59) 根据(8)式又得到一个随机系统 它的输入输出函数关系为 x1 可构造Fuzzy推理规则组 M≜max{f(x,y)|(x,y)∈X×Y}. 注意到 M=max{f(x,y)|(x,y)∈X×Y}= 即MH(2,n,θ,∨)=1.易证∀i∈{1,2,…,n},有 μ 自然得到B′=B.可见恢复了原本的Fuzzy推理规则组A→B.这是一方面的还原性. (60) 其中,λ=max{Δyj|j=1,2,…,n},Ai采用(12)式或(18)式构造,而Bi可取三角波形隶属函数(见图2).这时Fuzzy系统的输入输出函数一般为(注意比(16)式广泛) 这里Fuzzy蕴涵算子θ仍要满足条件(58)式.根据文献[1],得到一个随机系统 这里H(2,n,θ,∨)的意义同前.以下分两种情况考察还原性. 情况1按(18)式规定 Ai(x)≜f(x,yi)/M, 这时在Y的分点yj(j=1,2,…,n)上有 f′(x,y α(n)f(x,yj), (61) 对任意取定的划分,n固定,故α(n)为常数.(61)式说明在每个节点yj(j=1,2,…,n),f′(x,yj)除了一个常数因子α(n)外还原为f(x,yj).由于λ可任意减小,从而认为f′(x,y)除了一个常数因子外近似地还原为f(x,y). 情况 2按(12)式规定 μ 这时要求Y的分点yj(j=1,2,…,n)构成Y的等距划分,即Δyj=h,j=1,2,…,n.于是在Y的分点yj(j=1,2,…,n)上有 f′(x,y β(h)fη|ξ=x(yj|x), (62) f 为条件概率密度.根据上式,认为f′(x,y)除了一个常数因子外近似地还原为条件概率密度 fη|ξ=x(y|x). 注 6.1从常数β(h)≜h/H(2,n,θ,∨)的定义看,两个参数h与n是相关的.因此β(h)也可写成β(n),而不必写成β(h,n). 注 6.2注意f′(x,y)是个连续函数,不难从(61)式看出,f′(x,y)相当于在边缘Y中有定义的结点组 {(yj,α(n)f(x,yj))|j=1,2,…,n} 上的插值函数.在节点yj处,f′(x,y)严格地等于结点函数值α(n)f(x,yj).那么在非节点y处f′(x,y)对α(n)f(x,y)逼近的精度如何?这是个有趣的问题.另外,对于(62)式有类似的理解. 注 6.3上述情况2只还原到条件概率密度fη|ξ=x(y|x),似乎不令人满意.其实Fuzzy系统与随机系统之间的转换重在逼近程度优劣,如果完全还原或近似还原固然结果漂亮.不过还原到条件概率密度fη|ξ=x(y|x),也说明透过fη|ξ=x(y|x)揭示了f′(x,y)与f(x,y)之间的紧密联系. 从本文及文献[1]的内容可以发现一个现象:所涉及的概率密度至少是二维的,即至少涉及二维随机向量(ξ,η),其中ξ本质上定义在输入论域X,而η本质上定在输出论域Y.这并不奇怪,因为一个不确定系统至少是一个单输入单输出系统. 然而在学习概率论时见过很多的随机试验只涉及一个随机变量ξ,如其有密度函数,则是个一维密度函数f(x). 自然会问:什么样的不确定性系统只涉及一个随机变量,或者具有一维概率密度?可以猜想,这样的不确定性系统一定具有某种特殊性或具有某种意义的平凡性,而这样的系统会有很多.所以只能就几个典型情况来考察. 典型情况 1(纯粹确定性系统) 正如普通集可视为特殊的Fuzzy 集一样,确定性系统亦可看作特殊的不确定性系统.考虑一个特殊的开环系统s=S(X,Y),其中X=[a,b],Y={y0}为一个单点集.已经知道符号s具有双重含义,既抽象地代表一个系统,又具体地表示该系统的输入输出关系,即 s:X→Y,xy=s(x)≜y0. a=x1 将诸分点Fuzzy化,可按图2构造三角形Fuzzy集Ai∈F(X)(i=1,2,…,n)(注意要将图2中的n+1个下标0,1,…,n改为n个下标1,2,…,n).从而得到X上的Fuzzy划分 A={Ai|i=1,2,…,n}. 再作Y上的Fuzzy集 Bi≜Y={y0},i=1,2,…,n, 这里IY表示集合Y的示性函数(也叫特征函数,为了避免与概率论中随机变量的特征函数相混淆,宁可称其为示性函数).又得到 B={Bi|i=1,2,…,n}. 于是获得Fuzzy推理规则组:A→B.这样便得到了一个Fuzzy系统 为了简单,把Fuzzy蕴涵算子θ取为常用的∧,有 p(x,y)=p(x,y0)= 这时该Fuzzy系统的输入输出关系应该为 令 f(x)≜f(x,y0)= (63) 这样应该存在概率空间(X,F,P)上的随机变量 ξ:X→R,xξ(x) 服从概率密度为f(x)的概率分布,其中F为X上的 Borelσ-域.注意到,若令 Ω≜X×{y0}, 则F可视为Ω上的Borelσ-域,ξ视为定义在Ω上的随机变量,即不换记号重新定义 ξ:Ω→R, ω=(x,y0)ξ(ω)=ξ(x,y0)≜ξ(x), 只是形式上的表达,因为Y为单点集,其测度为零,故∀x∈X, 从而 即 无意义.不过这并不难处理.事实上,任取ε>0,易知 p(x,y0)>0, ∀x∈X, 由此可知,∀x∈X,有 p(x,y0)ε>0; 于是∀x∈X,又有 例 7.1考虑一个照明系统,为了简单,假定该系统只有一盏灯.通常在傍晚时将灯打开,假定开灯时刻介于a与b之间.令X=[a,b],视它为输入论域,那么取x∈X,则表示在时刻x把灯的开关闭合,这时灯亮,可记为1,视1为输出,自然取输出论域为Y={y0}={1}.当然灯用毕后要关上,而关闭动作不计其内.显然输入输出关系为 s:X→Y, xy=s(x)≜y0=1. 这当然是个纯粹的确定性系统.有理由要问:既然这个系统是确定性系统,那么为何出来个随机变量ξ以及它服从的概率密度为f(x)的概率分布?这也不难解释.如果把注意力集中在“究竟在X中的哪个时刻x把灯打开”,这又是个随机性问题,而这与确定性的输入输出关系 s:X→Y,xy=s(x)≜y0=1 并不矛盾.知道“傍晚在何时将灯打开”依赖许多因素,比如地区不同,开灯的时刻便不同.通过随机实验,可以大致知道在若干时刻附近,比如5点左右,6点左右,7点左右等有限种情况.一般化,可认为在x1左右,x2左右,…,xn左右开灯.记a=x1,b=xn,将诸xi(i=1,2,…,n)Fuzzy化,得到诸Fuzzy集 Ai∈F(X),i=1,2,…,n. 再作Y上的Fuzzy集 Bi≜Y={y0}, μBi(y)=χY(y)=χ{y0}(y),i=1,2,…,n, 又得到B={Bi|i=1,2,…,n}.于是获得Fuzzy推理规则组:A→B.这样便得到了一个Fuzzy系统 这便回到了获得(63)式的渠道.往下就不说自明了. 典型情况 2(纯粹随机系统) 考虑另外一个特殊的开环系统s=S(X,Y),其中X≜{x0}为一个单点集,Y=[a,b].它的输入输出关系应该为 s:X→Y,x0y0=s(x0). 然而,由于该系统的不确定性,x0对应Y中哪一个y0无法预先确知.所以s=S(X,Y)是一个纯粹的随机系统.当输入x0后,经过统计处理有这样几种情况:输出在y1左右,输出在y2左右,…,输出在yn左右.无妨假定 a=y0 将y0,y1,…,ynFuzzy化得到Fuzzy集 Bi∈F(Y),i=0,1,…,n, 且Bi为Y的Fuzzy划分.再令 Ai≜X={x0}, μAi(y)=χX(x)=χ{x0}(x),i=1,2,…,n, 并记A={Ai|i=1,2,…,n},以及B={Bi|i=1,2,…,n}(注意这里不用B0),得到Fuzzy推理规则组A→B,于是获得Fuzzy系统 按CRI方法有 p(x,y)=p(x0,y)= 因为∀y∈Y有p(x0,y)>0,所以 令 g(y)≜g(x0,y)= (64) 注意 该Fuzzy系统的输入输出关系应该为 这样应该存在概率空间(Y,F,P)上的随机变量η,它服从概率密度为g(y)的概率分布,其中F为Y上的Borelσ-域.同样,若令Ω≜{x0}×Y,则F可视为Ω上的Borelσ-域,η视为定义在Ω上的随机变量,而P亦可视为(Ω,F,P)上的概率.于是又得到随机系统 它的输入输出关系同样为 记Δyj≜yj-yj-1(j=1,2,…,n),有 (65) a=y0 Δyj=h,j=1,2,…,n 为等距时,又有 (66) 例 7.2考虑一个射击系统,为了简单假定该系统只有一只枪.每一次试验,即每一次操作,亦即每一次射击打一发子弹,子弹记为x0(因为同类型的枪打同类型的子弹,而同类型的子弹之间可不加区别,均记为x0),这样得到该系统输入论域X≜{x0}.每一次射击,子弹x0打向靶子理解为向该系统输入,靶子上的弹着点是该系统对于输入x0的响应,对于该响应的测量有多种方式;这里取弹着点到靶心的距离y为系统的输出.如果不算脱靶,弹着点到靶心的距离肯定有界,一个恰当的上界记为b(比如靶心到靶边缘的最大距离,在实际应用中要比它小),下界显然为a=0,于是又获得输出论域Y=[a,b].当该系统获得输入x0后,其相应的输出y0不能预先确知,故这是一个纯粹的随机问题.假如考察一个具有n个人的射击队的团体射击水平,经实验后发现每个射击队员的弹着点到靶心的距离分别为y1左右,y2左右,…,yn左右.无妨假定 a=y0 将y0,y1,…,ynFuzzy化得到Fuzzy集 Bi∈F(Y),i=0,1,…,n, 且Bi为Y的Fuzzy划分.再令 Ai≜X={x0}, μAi(x)=χX(x)=χ{x0}(x),i=1,2,…,n, 并记A≜{Ai|i=1,2,…,n},以及 B≜{Bi|i=1,2,…,n}, 现在考虑具有一维概率密度函数的随机系统的Fuzzy推理表示及其对随机系统的逼近问题.亦分两种情况. 典型情况 1*该情况与前述的典型情况1对偶.给定一个连续随机系统 这意味着存在概率空间(Ω,F,P)及定义在其上的随机变量ξ服从概率密度为 f(x)≜f(x,y0) 的概率分布,其中Ω≜X×{y0}.从前面的讨论已知该随机系统的输入输出关系为 其中假定∀x∈X有f(x,y0)>0,可见 作X的划分a=x1 Ai∈F(X),i=1,2,…,n, 使其构成X的Fuzzy划分.再作 Bi≜Y={y0}, μBi(y)=χY(y)=χ{y0}(y),i=1,2,…,n, 置A≜{Ai|i=1,2,…,n}以及 B≜{Bi|i=1,2,…,n}, 得到Fuzzy推理规则组A→B.于是便有Fuzzy系统 因为A≜{Ai|i=1,2,…,n}为X的Fuzzy划分,所以 该Fuzzy系统的输入输出关系为 典型情况 2*该情况与前述的典型情况2对偶.给定一个连续随机系统 这意味着存在概率空间(Ω,F,P)及定义在其上的随机变量η服从概率密度为 g(y)=g(x0,y) 的概率分布,其中Ω≜{x0}×Y.注意到 从前面的讨论知该随机系统的输入输出关系为 定理 7.1任意给定一个连续随机系统 一定存在一组Fuzzy推理规则:A→B,其中, A={Ai|i=1,2,…,n}, B={Bi|i=1,2,…,n}, Ai∈F(X),Bi∈F(Y),i=1,2,…,n, 证明首先作Y的划分 a=y0 构作三角形Fuzzy集 令M≜max{g(y)|y∈Y},再作分点yi,i=0,1,…,n的Fuzzy化: μ 显然Bi∈F(Y)(i=0,1,…,n).取 Ai≜{x0},i=1,2,…,n, A≜{Ai|i=1,2,…,n}, B≜{Bi|i=1,2,…,n}, 得到Fuzzy推理规则组A→B.于是做成Fuzzy系统 它的输入输出关系有下列表示: 因为 与 λ=max{Δyi=yi-yi-1|i=1,2,…,n}<δ, 就同时有 上一节的结论表明,Fuzzy系统与随机系统相互转换中还具有还原性.这意味着在系统的观点下,Fuzzy系统与随机系统是统一的,它们好像一个天平上的两个等量的砝码,各置该天平的托盘之一,其中一个砝码旧一点,而另一个砝码新一点.旧砝码意指概率论;新砝码则代表Fuzzy系统理论.它们各有侧重,互为补充,绝不相互排斥. 值得指出的是,面对一个不确定性系统,在概率论中要想获得关于该不确定性系统的概率分布是件相当困难的事情;然而,对于该不确定性系统,得到一组Fuzzy推理规则并不困难;由既得的Fuzzy推理规则组便可转化为该不确定性系统的概率密度,这是件极有意义的事情. 本文详细讨论了随机系统的Fuzzy推理表示问题,揭示了随机系统与Fuzzy推理之间有着紧密联系.主要结果如下. 1) 相对于不确定性系统,给出了随机系统的定义,它视为从随机系统的角度对一个不确定系统的逼近. 5) 面对一个不确定性系统,在概率论中要想获得关于该不确定性系统的概率分布是件相当困难的事情;然而,对于该不确定性系统,得到一组Fuzzy推理规则并不困难;由既得的Fuzzy推理规则组便可转化为该不确定性系统的概率分布,从而概率论中成熟的工具便可发挥作用了,这是件极有意义的事情.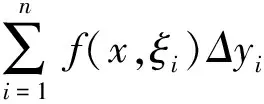
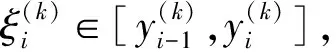


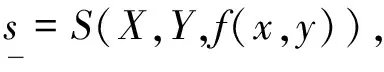

















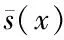

3 双输入单输出连续随机系统的Fuzzy 推理表示















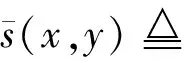


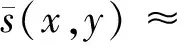
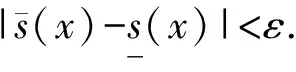
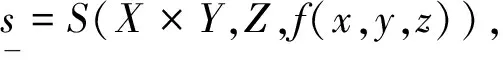



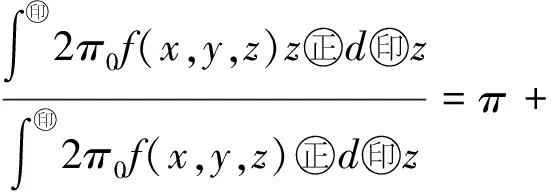


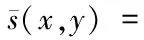


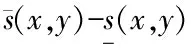

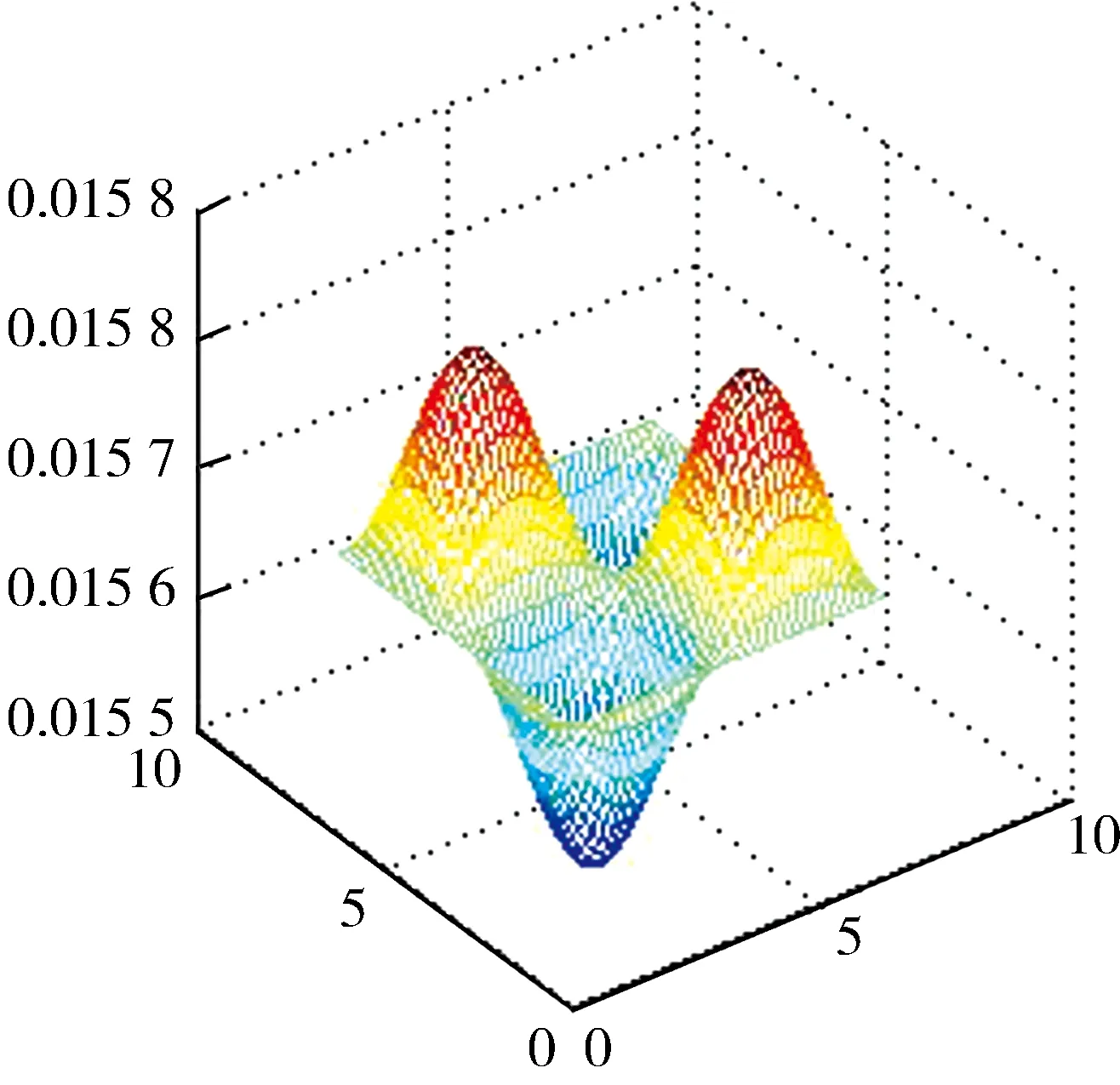
4 多输入多输出连续随机系统的Fuzzy 推理表示
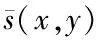
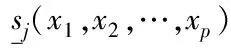

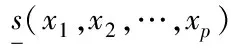




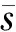
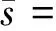
5 离散型随机系统的Fuzzy推理表示


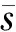
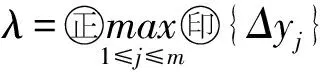

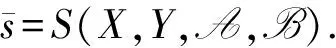
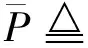
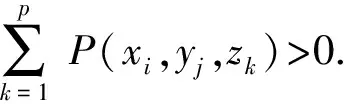
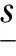
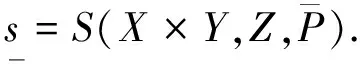
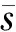


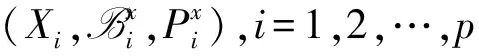
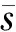

6 Fuzzy系统与随机系统转换中的还原性


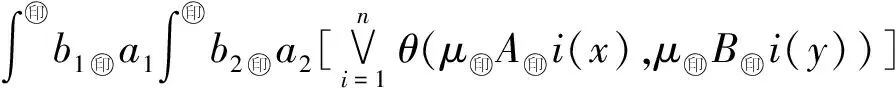




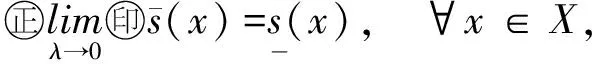


7 具有一维随机变量的不确定性系统及其表示
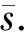
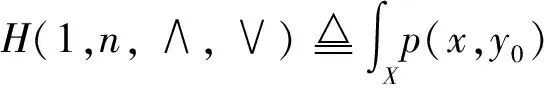

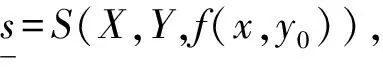









8 不确定性系统的统一性


9 结论