面向FT-M7002的一种Cholesky分解向量处理算法

李慧祥,张会福

(1.湖南科技大学 计算机科学与工程学院，湖南 湘潭，411201;2.湖南科技大学 服务计算与软件服务新技术湖南省重点实验室，湖南 湘潭，411201)

Cholesky分解是正定对称矩阵常用的矩阵三角分解方法，相比于通用的LU分解，其计算量约减少一半。因此，Cholesky分解广泛应用于正定对称线性方程组求解[1]、加速矩阵求逆[2]和Kalman滤波并行[3]等问题中。为了提高Cholesky分解算法的执行效率，研究人员对其进行了广泛的研究。吴荣腾[4]在多处理器平台上研究了Cholesky分解动态调度算法，解决各处理器之间的负载均衡问题。文献[5-7]在GPU(graphic processing unit)平台上采用小尺寸分块并行的方法加速Cholesky分解，减少CPU与GPU之间的数据通信时间。文献[8-10]基于FPGA(field programmable gate array)平台分析了Cholesky分解的数据依赖关系，设计了Cholesky分解的细粒度流水并行结构。由于处理器的硬件架构千差万别，Cholesky分解已有的优化方法并不能充分利用SIMD(single instruction multiple data)DSP的硬件资源，需要研究进一步的优化方法。

在SIMD体系结构的DSP中，由于多个并行单元共享一套取指、译码、派发逻辑，控制结构简单，可以有效降低硬件代价，能够在较低的功耗下获得较高的性能。近年来，国内的高性能DSP也取得了较大的成就，例如飞腾、龙芯、魂芯、申威等多个系列处理器。飞腾FT-M7002是国防科技大学微电子所自主研发的高性能SIMD DSP，其片上集成1个RISC CPU核和2个FT-MT2 DSP核，在1 GHz运行时，双精度浮点的峰值性能高达100 GFlops，单精度浮点的峰值性能高达200 GFlops[11]。硬件不断进步带来性能提升的同时，也对上层软件库提出了更高的要求。因此，根据硬件特点优化相应的算法软件，充分发挥出国产高性能DSP的硬件架构优势具有重要意义。

本文将结合FT-M7002处理器的硬件资源，研究Cholesky分解算法的优化。

1 Cholesky分解算法的基本原理

Cholesky分解的定义是：给定一个正定对称矩阵A，则存在唯一的主对角线元素全为正数的下三角矩阵L满足：

A=LLT

(1)

根据式(1)，对于任意一个对称正定矩阵都可以得到式(2)：

(2)

根据式(2)中矩阵乘法的运算规律，可以得到下三角矩阵L第j列更新的公式，见式(3)和式(4)。

(3)

(4)

2 FT-M7002处理器介绍

FT-M7002是一款40 nm工艺的高性能SIMD DSP，整个处理器使用三级存储结构。单个DSP核内拥有32 kB的标量存储空间(scalar memory，SM)和512 kB的向量存储空间(vector memory，VM)，所有的计算核共享2 MB的全局共享Cache，核外拥有32 GB的大容量DDR存储空间[12-13]。本文的相关研究基于单个DSP核。

FT-M7002的DSP核基于VLIW结构，包含一个五流出的标量处理器单元(scalar process unit,SPU)和一个六流出的向量处理单元(vector process unit,VPU)，两个处理单元以紧耦合的方式工作[13]，具体结构见图1。SPU只包含一个处理单元，主要负责串行任务处理和程序控制。VPU由16个向量计算引擎(vector process engine,VPE)构成，最多支持16路32位数据进行向量运算，主要面向密集型的计算提供并行处理。DMA(direct memory access)为内核提供了高速数据传输通路，实现核外DDR与SM和VM的快速数据交换。VM是VPU独享的数据存储器，在访存不冲突时，可以同时支持2个向量读/写，2个DMA读/写共4个并行请求。通过合理的数据排布，可以实现DMA传输和向量访存并行。

图1 FT-MT2 内核结构Fig.1 FT-MT2 kernel structure

FT-M7002具有大容量的VM、丰富的指令集、大宽度的向量运算和高效的数据传输等特点，在计算密集型的矩阵算法中能发挥出较大的优势。

3 基于FT-M7002的Cholesky分解实现与优化

3.1 Cholesky分解串行算法分析

根据式(3)、式(4)可以得到Cholesky分解生成下三角矩阵L的串行算法见算法1。分解结束后矩阵L存储在矩阵A的下三角位置，下面对矩阵L的更新将描述成矩阵A相应位置的更新。

算法1

Input:矩阵A, 矩阵A的阶数order

Output:矩阵A

Begin

1.forj=0:1:order

2./*对角线元素A[j,j]的更新*/

3.fork=0:1:j

4.A[j,j]=A[j,j]-A[j,k]×A[j,k]

5.endfor

6.A[j,j]=sqrt(A[j,j])

7. /*第j列其他元素A[i,j](i>j)的更新*/

8.fori=j+1∶1∶order

9.fork=0∶1∶j

10.A[i,j]=A[i,j]-A[i,k]×A[j,k]

11.endfor

12.A[i,j]=A[i,j]/A[j,j]

13.endfor

14.endfor

End

算法2

Input:矩阵A, 矩阵A的阶数order

Output:矩阵A

Begin

1.forj=0∶1∶order

2. /*对角线元素A[j,j]的更新*/

3.fork=0∶1∶j

4.A[j,j]=A[j,j]-A[k,j]×A[k,j]

5.endfor

6.A[j,j]=sqrt(A[j,j])

7. /*第j行其他元素A[j,i](i>j)的更新*/

8.fori=j+1∶1∶order

9.fork=0∶1∶j

10.A[j,i]=A[j,i]-A[k,i]×A[k,j]

11.endfor

12.A[j,i]=A[j,i]/A[j,j]

13.endfor

14.endfor

End

从算法1可以看出，矩阵A第j列的更新分为两个任务：1)对角线元素A[j,j]的更新；2)第j列其他元素A[i,j](i>j)的更新。第二个任务与第一个任务有数据依赖关系，二者只能串行执行。

算法1中共有3层嵌套循环，下文相关描述中最外层循环指的是forj=0∶1∶order。第一个中间层循环指的是fork=0∶1∶j，完成对角线元素A[i,j]的更新任务。第二个中间层循环指的是fori=j+1∶1∶order，完成第j列其他元素A[i,j]更新的任务。两个任务之间有数据依赖关系，二者只能串行执行。

第一个中间层循环是矩阵A第j行部分元素的平方和，循环结束后更新对角线元素A[j,j]。第二个中间层循环是一个二重循环，它外层循环的所有迭代更新矩阵A第j列其他元素A[i,j](i>j)，内层循环是矩阵A第i行和第j行部分元素的点积。可以看出：如果对它的内层循环进行展开，让多次循环迭代遍布在SIMD单元并行执行，那么在内层循环结束后需要对多个SIMD单元中的结果规约求和，一次完整的内层循环只能得到矩阵A第j列的一个标量结果，这种计算方式在SIMD DSP上的执行效率较低。如果对它的外层循环进行展开，让多次循环迭代遍布在SIMD单元并行执行，这样就可以将内层循环的点积转换成不同SIMD单元内部的乘累加操作，但是这种方式需要对矩阵A进行列访问，在并行存储器中这种非连续访存效率非常低下，仅为连续访存效率的1/15[14]。

综上所述，算法1直接映射到SIMD DSP上并不能充分利用处理器的硬件资源。考虑到矩阵对称的几何特征，可以按照同样的计算原理生成上三角矩阵来代替下三角矩阵L，在使用时只需把访问下三角矩阵的L[i,j]转换成访问上三角矩阵的LT[j,i]。经过上述转换，生成下三角矩阵L计算过程中对矩阵A的按列访问被转换成生成上三角矩阵LT计算过程中对矩阵A的按行访问，SIMD单元间的规约求和转换成SIMD单元内部的乘累加操作。根据算法1可以得到Cholesky分解生成上三角矩阵LT的串行算法见算法2，在算法2中，两个中间层循环分别完成两个任务：1)对角线元素A[j,j]的更新；2)第j行其他元素A[j,i](i>j)的更新。

3.2 基于FT-M7002的Cholesky分解优化

3.2.1 向量化方法设计

在对角线元素A[j,j]的更新任务中，为了减少对A[j,j]的重复访问，用一个局部变量vSum存储A[k,j]平方和的累加值，在循环结束之后再进行计算得到更新后的A[j,j]。需要注意的是，在存储A[j,j]时只开启第1个VPE，防止覆盖矩阵的有效数据。

在第j行其他元素A[j,i](i>j)的更新任务中，根据3.1节的算法分析，将第二个中间层循环的外层循环展开后，被展开的循环派发到所有的VPE上并行执行。对于多次循环中A[k,j]的重复访问问题，通过混洗单元将A[k,j]复制到所有的VPE中参与运算。同时为了减少内层循环对A[j,i]的重复访问，将0～j-1行的乘累加结果存储在局部变量vSum中。经过上述优化之后的伪代码见算法3，为了便于理解，算法3中没有描述出计算长度与处理器SIMD宽度不一致的代码。

在算法3中，mov_to_vlr(N)表示开启N个VPE，在FT-M7002上N最大为16。vec_mula()是乘累加函数，vSum=vec_mula(A[k,i],vtkj,vSum)的含义是vSum=A[k,j]×A[k,j]+vSum。shuffle()是混洗函数，通过配置特定的混洗模式，将向量变量中第一个值复制到所有的VPE中。

3.2.2 对角线元素更新任务的循环合并

在算法3中，第j行其他元素A[j,i](i>j)的更新任务已经充分向量化。但是在对角线元素A[j,j]的更新任务中，由于计算过程中只使用了一个VPE，浪费了大量的计算能力，需要对其进行优化。从外层循环分析，当j=0时，对角线A[j,j]的更新任务中只需要对对角线元素A[j,j]开根号，不需要累加第j列部分元素的平方和。当j=n+1时，对角线A[j,j]的更新任务中需要累加的第j列部分元素会在第j-1行其他元素A[j,i](i>j)的更新任务中访问到，见图2框中数据。

定义一个中间变量vDiag存储第j-1行其他元素A[j,i](i>j)更新任务中访问到的第一个值，这样可以直接消除对角线元素A[j,j]更新任务的循环，实现循环合并。循环合并后的伪代码见算法4。

算法3

Input: 矩阵A, 矩阵A的阶数order

Output:矩阵A

Begin

1.forj=0∶1∶order

2. /*对角线元素A[j,j]的更新*/

3.vSum=0

4.mov_to_vlr(1)

5.fork=0∶1∶j

6.vSum=vec_mula(A[k,j],A[k,j],vSum)

7.endfor

8.A[j,j]=sqrt(A[j,j]-vSum)

9.mov_to_vlr(N)

10. /*第j行其他元素A[j,i](i>j)的更新*/

11.fori=j+1:N:order

12.vSum=0

13.fork=0∶1∶j

14.vtkj=shuffle(A[k,j])

15.vSum=vec_mula(A[k,i],vtkj,vSum)

16.endfor

17.A[j,i]=(A[j,i]-vSum)/A[j,j]

18.endfor

19.endfor

End

算法4

Input:矩阵A, 矩阵A的阶数order

Output:矩阵A

Begin

1.vDiag=0

2.forj=0∶1∶order

3. /*对角线元素A[j,j]的更新*/

4.mov_to_vlr(1)

5.A[j,j]=sqrt(A[j,j]-vDiag)

6.mov_to_vlr(N)

7.vDiag=0

8. /*第j行其他元素A[j,i](i>j)的更新*/

9.fori=j+1∶N∶order

10.vSum=0

11.fork=0∶1∶j

12.vtkj=shuffle(A[k,j])

13.vSum=vec_mula(A[k,i],vtkj,vSum)

14.if(i=j+1)

15.vDiag=vec_mula(A[k,i],A[k,i],vDiag)

16.endif

17.endfor

18.A[j,i]=(A[j,i]-vSum)/A[j,j]

19.if(i=j+1)

20.vDiag=vec_mula(A[j,i],A[j,i],vDiag)

21.endif

22.endfor

23.endfor

End

算法4中相关函数的含义与算法3一致。在算法4中，通过在第j行其他元素A[j,i](i>j)的更新任务中以增加两个if分支为代价消除了对角线元素A[j,j]更新任务的循环，在后续的汇编代码中这两个if分支使用条件执行代替，消除跳转指令。

4 结果分析

为了体现优化后的算法在发挥处理器体系结构性能方面的表现，引入德州仪器(Texas Instruments,TI)的TMS320C6678处理器的库函数DSPF_sp_cholesky的性能进行对比，分析两类处理器的单核计算能力。

4.1 平台运行参数

算法2、算法3和算法4的性能是通过在FT-M7002开发板上运行手工汇编函数测得，TI平台的性能是通过在CCS5.5.0模拟器中选用TMS320C6678处理器运行库函数DSPF_sp_cholesky测得。平台运行参数见表1。

表1 实验平台参数Table 1 Experimental platform parameters

4.2 性能分析

实验测试了64、128、192、256、320和384阶矩阵的Cholesky分解，测得的节拍数见表2，其中算法2、算法3、算法4的汇编代码没有使用循环展开和软件流水等循环优化方法。

表2 Cholesky分解算法节拍数Table 2 The cycle of cholesky decomposition Algorithm

根据表2数据得到算法4相对于算法3、算法4相对于TI库函数、算法3相对于算法2的加速比,具体的折线图见图3，其中横坐标表示矩阵的阶数，纵坐标表示加速比。

从图3中算法3相对于算法2的加速比可以看出，在对算法2进行向量优化之后，优化后的算法(算法3)相对于串行算法(算法2)获得了7.21～12.81的加速比。从趋势上看，随着矩阵规模的增大，加速比先增加，最后趋于稳定。因为FT-M7002处理器共有16个VPE，理论上向量优化后的算法相对于串行算法最高能达到16倍的加速比。但是，由于本文的实验是将源数据放入核外DDR空间，在计算过程中由于数据传输耗时以及Cholesky分解算法本身会存在数据计算长度与SIMD宽度不对齐的情况，因此加速比达不到理论值，最后加速比稳定在13左右。

算法4在算法3的基础上消除了对角线元素A[j,j]更新任务的循环，对算法结构进行了优化。在图3的6组数据中，算法4相对于算法3获得了1.93～2.29的加速比。在算法4中，矩阵规模越大，对角线元素A[j,j]更新任务的循环耗时占比越小。因此，随着矩阵规模的增大，算法4相对于算法3的加速比缓慢减小。

图3中算法4相对于TI库函数只达到了1.90～2.82的加速比，并不是Cholesky分解算法在FT-M7002处理器上最佳的性能。循环展开和软件流水是常用的循环优化方法，二者搭配使用可以增加循环内指令的并行度，提高循环的执行效率。循环优化后的算法4相对于TI库函数获得了3.29～7.01的加速比，见图4，加速效果较为明显。

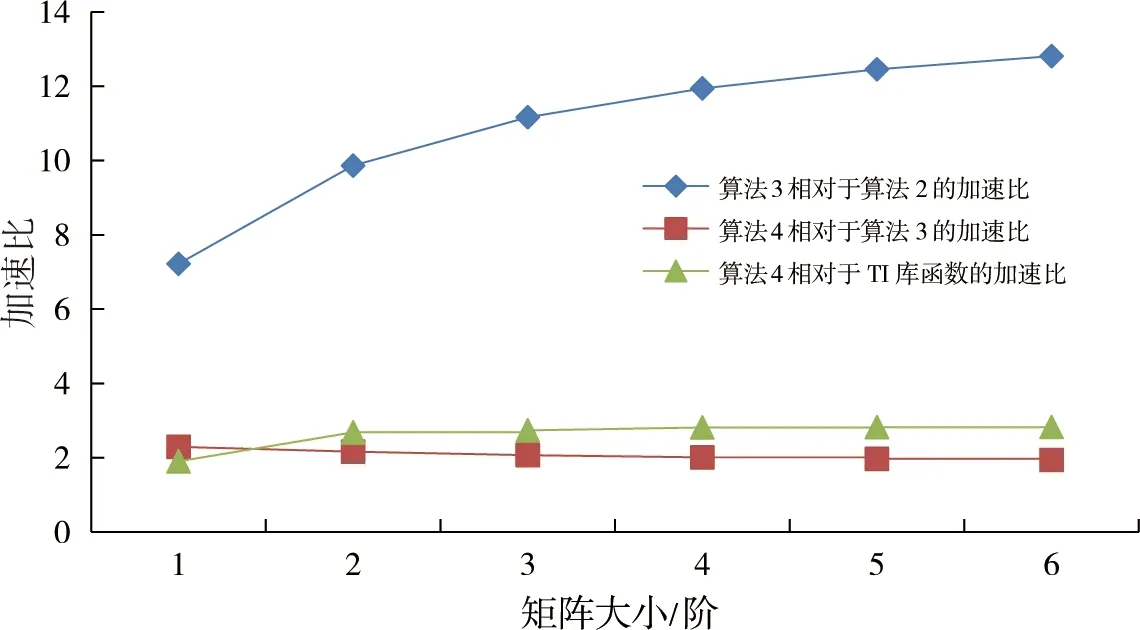
图3 算法加速比Fig.3 Algorithm speedup

图4 循环优化之后算法4相对于TI库函数的加速比Fig.4 Acceleration ratio of algorithm 4 relative to TI library function after cyclic optimization

5 结语

针对FT-M7002处理器向量SIMD处理的特点，研究了Cholesky分解算法的优化。根据矩阵对称的几何特征，提出生成上三角矩阵LT代替下三角矩阵L，避免了内存的非连续访问。分析了最外层循环相邻两次循环间的数据访问规律，消除了对角线元素更新的循环。结果表明：最终优化后的算法相对于TI库函数DSPF_sp_cholesky获得了3.29～7.01的加速比，加速效果较为明显。研究针对向量DSP单核的Cholesky分解算法的优化，有助于进一步研究针对多核情况相应的算法优化。