基于冲蚀耦合动网格方法的摇臂式喷灌喷头冲蚀变形数值模拟研究

申恒峰，黄剑峰，周传亮

(北部湾大学 建筑工程学院，广西 钦州 535011)

1 研究背景

在使用浑水进行喷灌的过程中，喷头由于持续地被冲蚀磨损会发生冲蚀变形，进而影响喷头的水力性能。目前对于喷头使用过程中各个阶段的冲蚀变形情况，以及冲蚀变形对喷头水力性能的具体影响程度的研究还不够全面。因此，本文通过探究喷灌喷头使用160 h内出口直径与出口流量之间的变化关系、出口直径与喷头射程之间的变化关系以及出口直径、出口断面形状系数与末端水滴之间的变化关系开展数值模拟研究。

我国对喷灌喷头的研究起步相对较晚[1]，诸多研究主要集中在喷头自身结构的优化[2-3]和组合模式创新[4]方面，近年来，喷头冲蚀变形问题也逐渐得到关注。为了探究泥沙对喷头的冲蚀磨损规律，李英能等[5]通过开展4组不同含沙量水流对喷头冲蚀磨损试验研究，分析了喷头流量、喷嘴磨损量和喷嘴尺寸与含沙量及冲蚀时间之间的关系；李红等[6]通过研究泥沙磨损对喷头可靠性的影响，得到了浑水质量浓度上升会使得喷头诸多水力性能变化率增加的结论，并认为提高喷嘴的耐磨性会使喷头的使用寿命延长；翟恩昱等[7]通过对固体颗粒做受力分析建立了运动方程，确定了固体颗粒对塑性材料喷头内表面冲蚀磨损时的速度。

鉴于开展冲蚀变形的物理试验研究较为困难，部分学者进行了相关的数值模拟分析。李文颖[8]、王子君[9]开展了8034D型喷头的冲蚀磨损试验研究和数值模拟，并进行了结果对比，但数值模拟并未考虑喷头的全流道流场，也未考虑喷头的冲蚀变形；Xu等[10]通过编写网格重塑程序，利用Fluent计算的冲蚀率数据更新壁面网格坐标，探究了喷头的冲蚀变形速率，发现时间步长对计算结果有较大影响。然而编写网格重塑程序一直是冲蚀变形研究的难点，于是石油管道领域的学者利用冲蚀耦合动网格方法进行构件冲蚀变形研究。Adedeji等[11]基于Oka冲蚀模型，结合冲蚀耦合动网格方法进行了弯管冲蚀变形研究，与试验结果对比后发现该方法可以准确预测构件的冲蚀变形；Wang等[12]通过将冲蚀耦合动网格方法应用到两个工程案例中，发现该方法在针对构件优化和预测构件寿命上具有可行性；孙岩等[13]利用该方法对绕丝筛管进行了冲蚀变形研究，分析了绕丝冲蚀变形发生的位置，并得到了不同冲蚀历时下绕丝的冲蚀变形情况。

综上所述，冲蚀耦合动网格方法的提出为开展喷头冲蚀变形的数值模拟研究提供了一种新思路，利用该方法研究喷头冲蚀变形规律及变形后对其水力性能的影响，可以为预测喷头使用寿命和喷头结构优化等提供参考依据。

2 研究方法

2.1 冲蚀耦合动网格方法

冲蚀耦合动网格是一种基于准稳态运行，并实现固-液-冲蚀完全耦合的构件变形计算方法。Fluent提供的冲蚀模型能够计算初始冲蚀率，目前已有诸多基于此模型开展的冲蚀磨损研究[14-15]。但冲蚀率实质上是瞬态的，因为冲蚀磨损是一个持续的动态过程，所以预测较长时间后的冲蚀率需要考虑构件的冲蚀变形。冲蚀耦合动网格方法是通过将总冲蚀时间拆分，并在每一段时间上计算出壁面冲蚀率，然后据此更新壁面网格坐标，而壁面网格坐标则通过动态网格子模型基于物理时间步长实现更新。

耦合动网格方法首先需要在稳态条件下计算得到喷头的壁面冲蚀率等数据，在开始动态网格冲蚀计算后，网格的坐标位置会根据设定的时间步长内喷头壁面冲蚀率进行更新，其计算流程如图1所示，单个单元面的变形量由以下公式计算：

图1 喷头变形量计算流程

(1)

式中：Δxface网格单元变形量，m；Δtmm为网格运动时间步长，s；Eface为特定时间步长的壁面冲蚀率，kg/(m2·s)；Δtmm为计算时段，s；ρwm为被冲蚀靶材的密度，kg/m3。

2.2 湍流模型及冲蚀模型

利用标准k-ε湍流模型对喷头不同工况进行模拟，该模型适用性较好[16]，由湍流脉动能k和扩散率ε组成，在实际工程中应用广泛，其准确性得到了较好的验证。选用DPM(deformable part model)作为离散相模型[17]，其提供了Generic、Mclaury、Oka和Dnv等冲蚀模型，选用其中适用范围较广的Generic模型，该模型由Huser等[18]提出，冲蚀率被定义为：

(2)

式中：mp为颗粒质量流量，kg/s；C(dp)为颗粒粒径函数；α为颗粒路径与壁面的冲击角，(°)；f(α)为冲击角函数；v为颗粒相对速度，m/s；b(v)为颗粒相对速度函数；Aface为壁面面积，m2。

2.3 求解方法与边界条件

研究基于有限体积法对控制方程进行离散，利用SIMPLEC算法对速度和压力进行耦合求解，扩散项采用二阶中心差分格式，对流项采用二阶迎风格式。分别设置压力入口和出口，入口压力设为350 kPa。设置连续相为清水，其密度为998 kg/m3，颗粒密度为2 650 kg/m3。

2.4 几何模型与网格划分

首先对PY1-20sh型喷头进行全流道三维建模，模型尺寸比例为1 ∶1，具体模型几何参数如图2(a)所示。由于DPM模型的局限性，无法计算壁面边界处的冲蚀率，使得正常情况下无法预测出口直径的变化，因此需考虑喷嘴约为0.2 mm的实际壁面厚度，且仍以原始出口断面面积计算出口当量直径。

不考虑喷头内螺纹等细部结构，假设各部分连续光滑，利用ICEM软件对几何模型进行六面体非结构化网格划分，如图2(b)所示。通过多次网格划分并以相同初始条件计算出口流量进行网格密度分析，计算结果见表1，考虑在保证精度的前提下节约计算资源，最终取网格数为91 808。

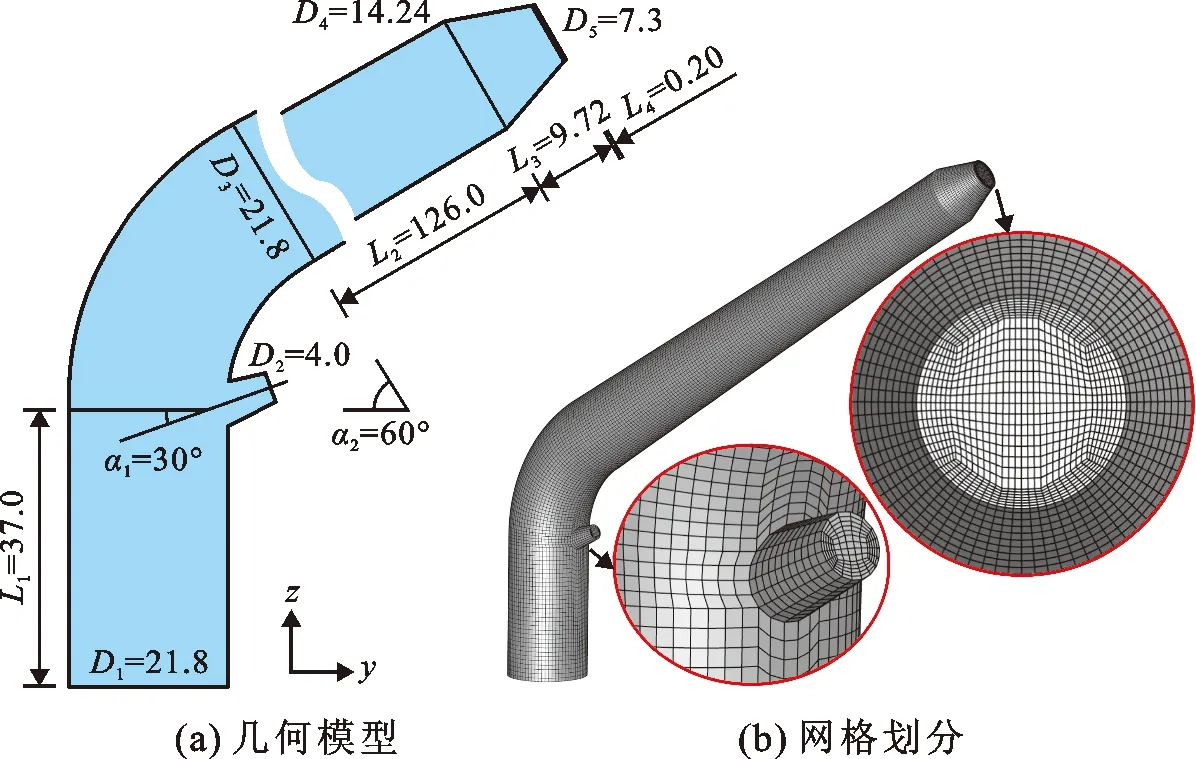
图2 喷头模型几何参数及三维模型网格划分(单位：mm)

表1 网格密度分析

3 冲蚀条件设置与理论计算公式

3.1 颗粒属性与时间步长设置

参考林管[19]对PY1-20sh型喷头开展的冲蚀磨损试验研究，本文设置与其一致的初始条件，并通过结果对比验证本文数值模拟结果的可靠性，表2为具体的颗粒注入参数。

表2 喷头冲蚀磨损数值模型颗粒注入参数

文献[19]的试验过程中泥沙颗粒不断发生碰撞破碎，使颗粒级配始终在发生变化，表2中的颗粒级配为综合考虑后的取值。同时设置颗粒由喷头入口注入，颗粒速度与水流流速一致，水流含沙量设3组数据，分别为2.5、5.0和7.5 kg/m3。

选用固定时间步长进行冲蚀变形计算，并与自适应时间步长的计算结果进行对比。通过分析喷头累计平均变形量来选择合理的时间步开展进一步分析，表3为各时间步长计算的累计平均变形量。计算中设置总冲蚀历时为160 h，以40 h为时间间隔，冲蚀耦合动网格平滑步数为5步，每个流动迭代次数为100次。

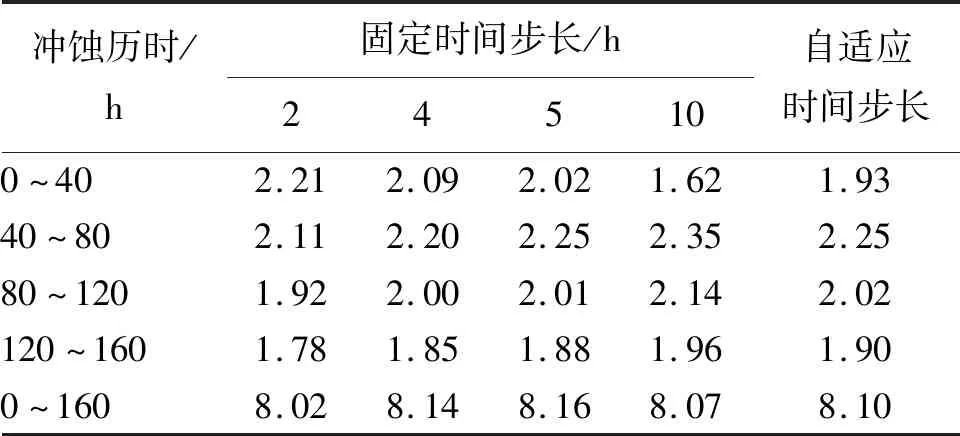
表3 各时间步长变形量计算结果10-6m

由表3可以看出，各时间步长计算的0～160 h累计平均变形量结果比较接近，只有时间步长为2 h时离散度相对较大，时间步长为5 h时离散度相对最小，因此选用时间步长为5 h。

3.2 主喷嘴出口直径及直径增加率计算

通过出口断面面积计算出口当量直径：

(3)

式中：D为主喷嘴出口当量直径，m；A为主喷嘴出口断面面积，m2(该断面位置的选取见后文图6)。

直径增加率计算公式为：

ηD=(Dt-D0)/D0×100%

(4)

式中：ηD为直径增加率；Dt和D0分别为t时刻与初始时刻主喷嘴出口直径，m。

3.3 质量损失计算

由内流道体积变化计算质量损失：

Δm=ρ(V1-V0)

(5)

式中：ρ为壁面材料密度，该喷头壁面材料为铸铝，密度为2 719 kg/m3；V0和V1分别为冲蚀前、后的喷头内流场体积，m3。

3.4 流量增加率及主喷嘴流量系数计算

流量增加率计算公式为：

ηQ=(Qt-Q0)/Q0×100%

(6)

式中：ηQ为流量增加率，%；Qt和Q0分别为t时刻和初始时刻喷嘴出口的总流量，m3/h。

流量系数计算公式为：

(7)

式中：μ为主喷嘴流量系数；Qm为主喷嘴流量，m3/h；A为主喷嘴出口断面面积，m2；h为喷头压力水头，m。

3.5 喷头射程理论计算

喷头射程的理论计算模型较多[20-22]，冯传达[23]基于对PY1-20sh型喷头开展的试验研究提出了射程计算公式，因与本文研究喷头类型一致，所以有较好的适用性，该公式为：

(8)

式中：R为喷头射程，m；μ为主喷嘴流量系数；H0为主喷嘴出口压力水头，m；θ为喷头仰角，(°)；D为主喷嘴当量直径，mm。

3.6 形状系数与末端水滴直径理论计算

喷嘴的形状常用形状系数β进行描述，β值越大说明喷嘴出口断面越偏离圆形，对末端水滴直径影响越大[24]，其计算公式为：

(9)

目前，部分学者已进行了喷头水滴分布的理论研究[25-26]，其中比较全面地考虑各影响因素的李久生[27]公式为：

(10)

式中：dm为末端水滴直径，m；D为主喷嘴当量直径，mm；h为喷头工作压力水头，m；β为主喷嘴形状系数；μ为主喷嘴流量系数；R为射程，m。

4 结果与分析

4.1 喷头冲蚀磨损部位分析

进行喷头全流道计算模型的建立可以更真实地反映喷头内部流体流动情况，获得更准确的颗粒运动轨迹。但由于喷头整体结构相对较大且冲蚀磨损分布并不均匀，不利于分析冲蚀变形相对严重的局部位置，又因为冲蚀变形的计算基于冲蚀率基础数据，因此首先进行冲蚀率分布分析以确定喷头主要冲蚀磨损部位，从而进一步探究该部位的冲蚀变形情况。图3为喷头内流场中沿流程方向的DPM颗粒浓度和冲蚀率分布图。

图3 喷头内沿流程方向DPM浓度与冲蚀率分布

由图3可以看到，喷头内流场中DPM浓度随着喷头管径的缩小呈微弱增大的趋势，在两个喷嘴处浓度较大。通常情况下DPM浓度与壁面碰撞率呈正相关关系，颗粒碰撞次数越多则冲蚀率相对越大。但冲蚀磨损的产生是诸多因素共同作用的结果，可以看到冲蚀率从副喷嘴附近开始增大，主喷嘴附近冲蚀率最大。为了更准确地解释上述情况需要结合喷头内的流场情况进行分析，图4为喷头内流场中的流速和压力分布。

由图4可知，出现上述情况是因为喷头入口附近速度较小，仅约为2 m/s，水流对泥沙曳力较小，此时泥沙动能较小，所以该段没有发生较大冲蚀磨损。主喷嘴附近由于管径大幅收缩，流速突增，压力减小，使得水流流态紊乱，增加了泥沙与壁面碰撞概率，导致该处冲蚀磨损严重。

图4 喷头内的速度与压力分布云图

为了分析在水流不同含沙量情况下喷头冲蚀率分布情况，选择2.5、5.0、7.5 kg/m33组含沙量工况进行研究，3组含沙量下主喷嘴冲蚀率分布如图5所示。由图5可见，主喷嘴的冲蚀程度随着含沙量的增大而逐步加深，但主喷嘴整体的冲蚀率分布未发生明显变化，始终主要分布于主喷嘴收缩段。

图5 水流不同含沙量时主喷嘴冲蚀率分布

4.2 主喷嘴冲蚀变形分析

通过分析喷头冲蚀率分布可知冲蚀磨损主要集中在主喷嘴处。因此，为了更清晰地观察喷头局部冲蚀变形情况，需分别探究主喷嘴在3组含沙量工况下不同冲蚀历时的累计平均变形量变化规律，并结合不同时间节点的冲蚀率变化进行对比分析。图6为喷头在含沙量7.5 kg/m3下冲蚀160 h的主喷嘴累计变形量分布云图，图7为水流不同含沙量时不同冲蚀时段主喷嘴累计平均冲蚀变形总量和增量以及冲蚀率随历时变化图。

由图6可以看出，主喷嘴网格冲蚀变形程度与冲蚀变形量分布十分吻合，出口收缩段发生了较大的变形，该变形表现为主喷嘴壁面整体向外不均匀膨胀扩张，使得喷嘴内流道体积增大。出现该现象的原因是由于收缩段增大了颗粒与壁面的碰撞角度，使颗粒趋向于正面碰撞而加深了壁面的冲蚀程度，流道体积扩大的根本原因是壁面材料从表面逐渐剥离。

由图7可知，主喷嘴平均累计变形量随着水流含沙量的增大而逐渐增大。同时，在160 h的冲蚀过程中，不同时间节点的平均冲蚀率逐渐减小。这可能是因为冲蚀变形会改变主喷嘴壁面结构，而变形后的壁面结构会避免与一部分泥沙颗粒的碰撞，从而减缓了该区域后续变形的发生。因此主喷嘴每40 h的累计平均变形量表现为逐渐减小，且随着水流含沙量的增大这种变化规律愈加明显。3组含沙量水流冲蚀160 h后主喷嘴累计平均变形量分别约为5.6×10-6、1.0×10-5和1.3×10-5m。

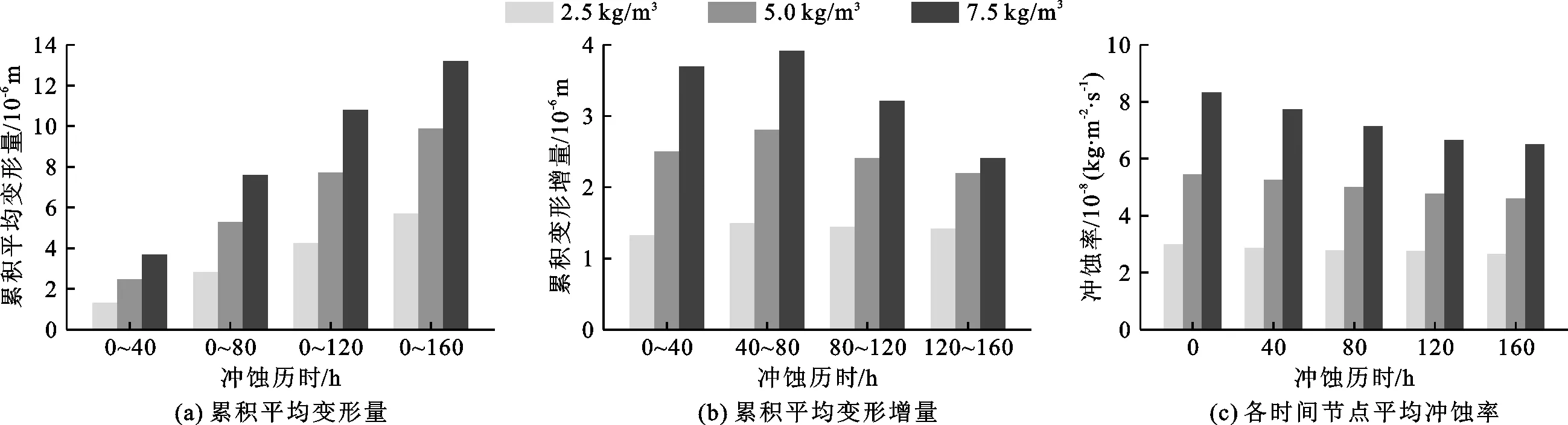
图7 水流不同含沙量时主喷嘴变形情况随冲蚀历时的变化

4.3 喷头总质量、出口直径与出口流量变化分析

冲蚀变形的本质是壁面材料逐渐从表面剥离，可以通过计算喷头质量损失进行该过程的分析。同时，为了进一步定量分析主喷嘴的冲蚀变形，需要计算主喷嘴出口直径增加率，而出口直径的扩大将对出口流量造成影响，通常情况会使出口流量增大，诸多研究表明大部分型号的喷头出口流量变化率超过10%便达到报废的条件。表4为160 h内3组含沙量水流不同冲蚀历时的喷头出口直径、质量及出口流量的试验与模拟计算结果。

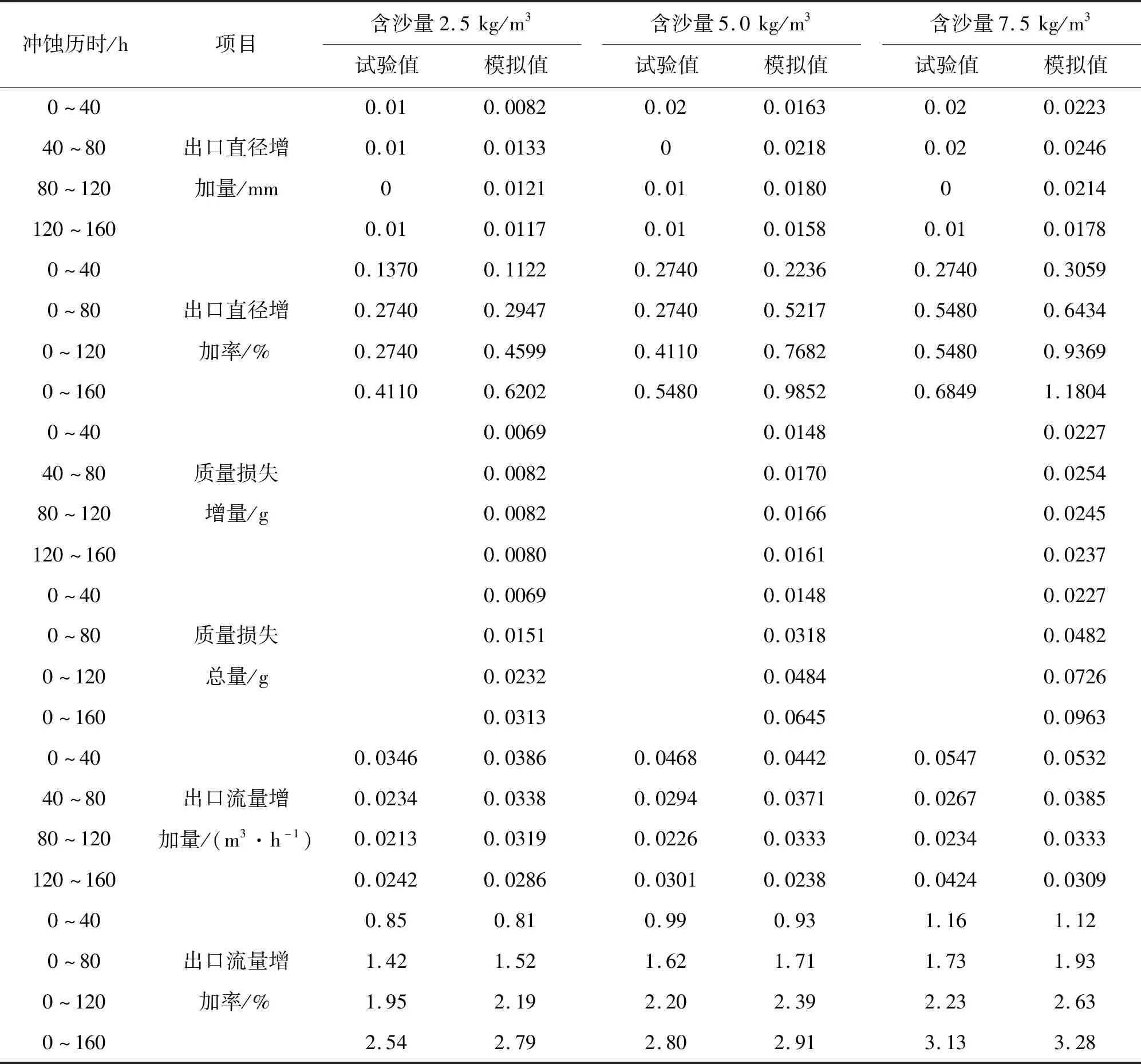
表4 3组含沙量水流不同冲蚀历时的喷头出口直径、质量及出口流量的试验与模拟计算结果

由表4可知，喷头质量损失总量与含沙量大小以及冲蚀时间均呈正相关，每40 h的质量损失增量与含沙量大小呈正相关，与冲蚀时间无明显线性关系，且质量损失增量变化随冲蚀时间的延长而逐渐趋于平稳，这是由于喷头后期的冲蚀磨损强度逐渐减弱所致。在3组含沙量水流冲蚀160 h后的喷头质量损失总量分别约为0.031、0.065和0.096 g，换算后可知其质量损失速率分别约为0.19、0.41 与0.60 mg/h。表4的计算结果表明，喷嘴运行早期出口直径增量较大，随冲蚀历时的延长逐渐趋于平稳。林管[19]的试验结果可能由于测量精度原因没有记录小于0.01 mm的直径变化，使得部分时间段内的直径增量表现为零。3组含沙量水流冲蚀160 h后直径增加率分别约为0.62%、0.98%和1.18%，略大于文献[19]的试验结果，但仍在合理范围内。喷嘴部分通常需要设计管径收缩段以更好地控制水流，但也增加了该段的冲蚀磨损，而由于收缩段冲蚀变形导致的出口直径增大将会造成喷头诸多水力性能的改变，其中影响最大的是喷头出口流量。

数值计算的喷头初始流量略大于文献[19]的试验结果，但误差约1.1%在合理范围内。通过分析表4的出口流量增加率可知，出口流量与出口直径随冲蚀历时的变化趋势具有一致性，在3组含沙量水流冲蚀160 h后喷头流量增加率分别约为2.79%、2.91%和3.28%，每40 h的流量增量逐渐减小，数值计算结果与文献[19]的试验结果整体较为吻合。在工作压力不变的情况下出口流量增加说明喷头对水流的控制能力变差，将改变喷嘴出口断面的水流平均速度大小，通过分析流量系数变化可以看到喷头能量损失增加的过程。图8为3组含沙量水流条件下主喷嘴流量系数μ随冲蚀历时变化的计算结果。

如图8所示，主喷嘴的流量系数随冲蚀历时的增加而逐渐减小，在3组含沙量下运行160 h后流量系数分别减小约0.9%、1.6%和2.2%，流量系数综合反映了出口直径、工作压力和出口流量之间的关系，该系数的减小说明喷头的能量转化效率降低。

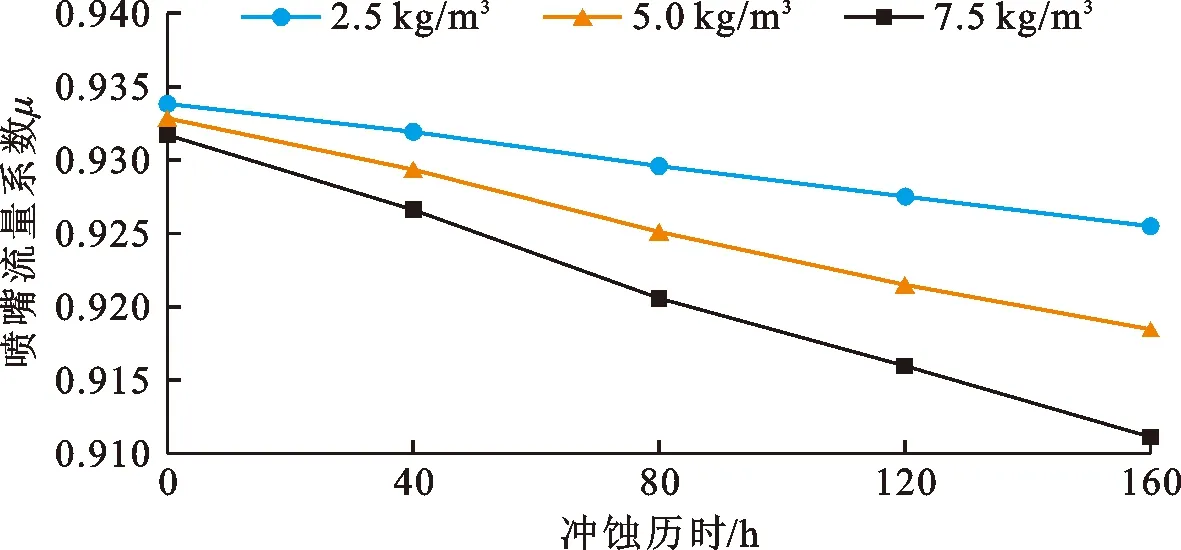
图8 水流不同含沙量时主喷嘴流量系数随冲蚀历时的变化曲线

4.4 喷头射程与末端水滴直径变化理论分析

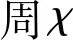
图9 水流不同含沙量时主喷嘴的射程、出口断面湿周和形状系数随冲蚀历时的变化曲线

由图9(a)可知，喷头射程随冲蚀历时的延长而逐渐缩短，经过160 h冲蚀后，水流含沙量为7.5 kg/m3时的射程减幅最大，缩短了1.03 m，3组含沙量射程分别缩短约1.4%、2.6%和3.8%。喷头射程的缩短会大幅减少原本灌溉范围内距离喷头安放中心较远区域的洒水量，其次由于喷嘴出口断面流速梯度减小，会增加原本灌溉范围内中间区域的洒水量，减少喷头安放中心附近的洒水量，从而影响灌溉质量。

由图9(b)可知，喷嘴出口断面湿周随冲蚀历时的增加而逐渐变大，3组含沙量水流冲蚀160 h后出口断面湿周分别增大了0.79%，1.35%和1.82%。断面湿周的增大使得水流与喷嘴壁面的接触面积增加，而出口平均流速、湍动能等物理量均受边壁的影响较大，是造成水流能量损耗的主要原因。

由图9(c)可知，主喷嘴出口形状系数变化相对较小且随冲蚀历时的延长出现一定的波动，但整体上在逐渐增大，出现该变化是因为主喷嘴的冲蚀变形主要发生在局部位置，但随冲蚀历时的延长局部冲蚀位置发生了转移，使喷头出口断面形状获得一定程度的复原。形状系数是影响喷头末端水滴直径的重要因素，为了探究具体的影响需进行喷头冲蚀160 h内的末端水滴直径理论计算，图10为相应的计算结果。

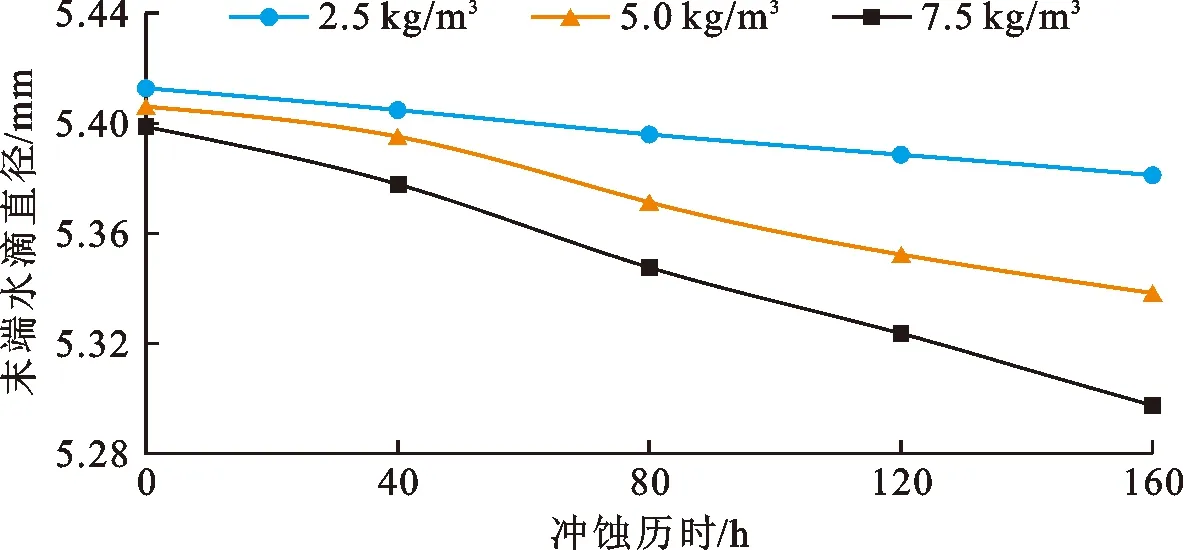
图10 水流不同含沙量时主喷嘴末端水滴直径随冲蚀历时的变化曲线

由图10可看出，喷头末端水滴直径随冲蚀历时的延长而逐渐减小，但减小幅度相对较小，3组含沙量水流冲蚀160 h后喷头末端水滴直径分别减小了0.6%、1.3%和1.9%，说明喷头的冲蚀变形对其末端水滴直径的影响十分有限。

由理论计算公式(公式(10))可以看出，喷头末端水滴直径受到结构尺寸影响的因素分别为出口当量直径D和出口断面形状系数β，其中形状系数β对末端水滴直径影响的比重较大，但由于通常情况下喷嘴出口断面的形状系数并不会发生较大变化，所以水滴直径并未受到明显的影响。另外，末端水滴直径减小会增强喷头的雾化效果，减小水滴对作物的打击力度。

5 结 论

利用冲蚀耦合动网格方法对PY1-20sh型喷灌喷头进行冲蚀变形计算，实现了固-液-冲蚀-网格运动的完全耦合，通过模拟喷头在运行160 h内的冲蚀变形发展过程，并利用变形后的网格文件进行喷头水力性能变化的研究，得出以下主要结论：

(1) PY1-20sh喷头在运行过程中，主喷嘴收缩段持续地受到冲蚀磨损，造成喷嘴流道体积和出口直径增大以及出口形状小幅度偏离圆形，这些变形会在不同程度上对喷头的水力性能产生影响。其中出口直径的变化是影响喷头水力性能的主要原因，其对出口流量的影响十分明显，也是导致喷头报废的主要因素。出口直径和出口形状系数的变化对喷头射程和末端水滴直径未造成明显影响。

(2) 数值模拟的喷头出口直径和流量变化结果与林管[19]的试验结果整体上相吻合，说明冲蚀耦合动网格方法用于计算喷头冲蚀变形具有可行性，该方法对解决工程实际问题有较大的意义和应用价值。今后可利用该方法进一步对喷头的抗冲蚀变形结构优化进行研究。