鄱阳湖修河虬津水文站非一致性设计洪水研究

吴绍飞，罗 文，熊凡迪，欧阳芬，黄彬彬

(南昌工程学院 鄱阳湖流域水工程安全与资源高效利用国家地方联合工程实验室，江西 南昌 330099)

1 研究背景

在气候变化与人类活动的影响下，暴雨、洪水等水文极值事件常表现为显著非一致性[1-3]，基于独立同分布假设的一致性设计洪水计算结果将增加工程风险或导致经济上的浪费[4-5]，非一致性水文频率计算方法成为水文科学研究的热点[3]。

在众多研究中，基于非一致性水文系列直接进行水文频率计算越来越受到国内外学者的重视，此类方法主要包含两类，即分布函数加权综合法(如混合分布法、条件概率模型法等)和变参数模型法(如时变矩法)[6]。王军等[7]重建了淮河流域530 a夏季降水系列，引入混合分布构建了一个包含4个子平稳系列的综合概率分布，结果表明，混合分布模型对观测系列具有较好的拟合效果，在一定程度上解决了水文要素变异前后的非同分布问题，但分布函数参数较多，采用常规方法估计困难；宋松柏等[8]发展了适用于具有跳跃变异的非一致性概率分布频率计算公式，此类方法适用于因数据缺失或气候差异等造成的非一致性水文系列频率计算问题；He等[9]以新疆马斯纳河流域为例，系统研究了P-Ⅲ分布、混合分布及条件概率模型法在非一致性洪水频率分析中的适用性；Strupczewski等[10]探索了在非一致性洪水频率分析中应用时变矩模型的可行性；Rigby等提出了基于位置、尺度和形状的广义可加GAMLSS(generalized additive models for location scale and shape)模型[11]，该法是时变矩法的进一步发展，在非一致性水文频率计算中得到广泛应用[11-13]。然而，在上述基于时变矩的非一致性水文频率计算框架下，给定的设计标准或重现期所对应的设计值并不是一个常数，将随着协变量的变化而变化，其结果很难直接应用到实际工程水文设计中[14]，重现期的期望超过次数法(expected number of exceedances,ENE)是解决上述问题的有效方法之一[15]。

本文以鄱阳湖修河虬津站1956-2014年最大1、3、7、15 d和1个月最大洪水系列(QMax 1d、QMax 3d、QMax 7d、QMax 15d和QMax 1m)为例，引入ENE方法，系统研究虬津站多时间尺度的设计洪水问题，以期为该区域洪灾防治和水利工程管理提供依据。

2 数据来源与研究方法

2.1 研究区概况

修河(图1)为鄱阳湖“五河”之一，地处亚热带季风气候区，多年平均降水量约为1 660 mm，其中4-6月降水量约占全年降水量的50%。修河干流下游虬津水文站以上流域面积为9 914 km2，约占修河流域总面积的70%，该水文站实测最大洪峰流量为3 420 m3/s(1998年8月1日)。

图1 鄱阳湖修河流域概况

2.2 数据来源

本研究主要采用以下3种数据：(1)实测水文数据；(2)研究区内实测降水量、气温等数据；(3)CMIP5(Coupled Model Intercomparison Project 5)大气环流模型GCM(geheral circulation model)输出数据，其来源分别如下。

(1)虬津站1956-2014年日平均流量数据来自江西省水文监测中心，分别选取该时段年最大1 d、最大连续3 d、最大连续7 d，最大连续15 d和最大连续1个月的流量系列作为洪水极值进行研究(限于篇幅，仅列出最大连续1个月洪水总量系列Max 1m，见图2(a)，下同)。

(2)选取影响径流的两个主要气象要素(降水量和气温)为协变量，构建洪水系列非一致性分布模型。其中降水数据为利用泰森多边形法计算的流域内有代表性的气象站日降水系列面平均值，气温数据采用修河气象站日气温数据，并进一步选取年均降水量(P)和年均气温(T)作为非一致性洪水频率分析的协变量(图2(b)、2(c))。

图2 虬津水文站实测洪水系列及其与降水量、气温的相关关系

(3)GCM 输出数据选取政府间气候变化专门委员会(Intergovernmental Panel on Climate Change,IPCC)第5次评估报告中RCP4.5(representative concentration pathway 4.5)和RCP8.5(representative concentration pathway 8.5)两种排放情景下40个模型2010-2099 年与美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)相应的大尺度预报因子，具体处理过程见文献[16]。

2.3 研究方法

2.3.1 基于位置、尺度和形状参数的广义可加模型 GAMLSS模型主要用于刻画随机变量统计参数与协变量之间的线性或非线性关系[10-11]，其主要原理如下：

假设GAMLSS模型在时刻t(t=1,2,…,n)的独立随机变量观测值zt服从概率密度函数f(zt|θt)，其中，θt=(θt1,θt2,…,θtp)为t时刻的p个分布统计参数向量，θk=(θ1k,θ2k,…,θnk)T为所有时刻的第k个(k=1,2,…,p)统计参数所组成的向量，而gk(·)为一个单调可微的连接函数。则在忽略随机效应项的前提下，θk为Yk的单调函数：

gk(θk)=ηk=Ykβk

(1)

式中：ηk为长度为η的向量;Ik为协变量个数;Yk为n×Ik的矩阵;βk=(β1k,β2k,…,βIkk)T为长度为Ik的向量。

在实际进行非一致性水文频率分析时，常用参数p≤3的分布函数，于是参数统计向量可以进一步表示为θt=(μt,σt,τt)，其中μt，σt，τt分别为GAMLSS模型中的位置参数、尺度参数和形状参数。将各参数带入函数式(1)，则gk(θk)可表达为：

(2)

其中，协变量矩阵Yk为：

(3)

将公式(3)代入公式(2)，得到如下函数关系(仅以μt为例)：

(4)

公式(1)～ (4)给出了以时间t为协变量的非一致性模型构建框架。由于以时间t为协变量的GAMLSS模型缺乏物理意义，本研究引入年均降水量(P)、年均气温(T)等气象因子构建洪水系列协变量。同时，引入水文学中3种常用的分布函数：对数正态分布LOGNO、伽马分布GA、耿贝尔分布GU，作为洪水极值系列备选理论分布(表1)，各模型拟合效果采用虫图和AIC值综合判定。

表1 常用的两参数分布函数表

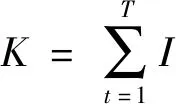
(5)

由上式可知，K的期望值E(K)为1，因此E(K)的表达式为：

(6)

在一致性条件下，超过初始设计值的ENE重现期为T=1/p0。

在非一致性条件下，初始设计值Zp0的超过概率Pt会随时间发生变化，因此期望E(K)的表达式为：

3 结果与分析

3.1 虬津站考虑气象要素的非一致性GAMLSS模型

基于水文变异综合诊断系统，周秋红等[17]系统研究了虬津站1956-2014年多时间尺度径流变异情况，结果表明，虬津站各时间尺度径流系列均表现出显著跳跃变异。在引起该站洪水系列变异的各类因素中，文献[17]进一步指出气象因素的要素主要是年总降水量，年均气温对研究区域短历时洪水极值系列有显著影响。因此，本文以流域内年均降水量P和年均气温T为协变量，以LOGNO，GA和 GU作为各列备选分布线型，并以 AIC值大小比较各模型拟合的优劣，建立了虬津站上述各系列最优非一致性GAMLSS统计模型，如表2所示。

以QMax 1d系列为例，由表2可知，考虑P和T为协变量的统计模型，AIC评价准则表明GA分布为最优分布，且统计参数μ为P、T的线性函数(统计参数σ为常数)时为最优非一致性统计模型。进一步计算表明，在仅考虑线性函数关系的前提下，与以时间为协变量的模型相比，以P和T为协变量的GAMLSS模型具有更小的AIC值。研究区域QMax 3d和QMax 1m系列最优分布函数也为GA分布，QMax 7d和QMax 15d系列最优分布函数为LOGNO分布。杜涛等[18]指出，引入具有物理意义的气象因子作为协变量，不仅能够拟合出洪水系列的下降趋势，还可以更好地描述洪水系列的周期波动。由表2还可以看出，各时间尺度洪水流量系列位置参数均存在显著的非一致性，QMax 1d、QMax 3d和QMax 1m系列最优分布模型位置参数均为年总降水量和年均气温的线性函数，QMax 7d和QMax 15d系列最优分布模型位置参数均为年总降水量的线性函数。各时间尺度洪水流量系列尺度参数不存在显著的非一致性(QMax 7d系列除外)。此外，为了与不考虑系列非一致性的结果进行对比，表2还给出了相应的一致性统计模型参数。

表2 虬津站实测各洪水系列一致性和非一致性频率统计模型

3.2 修河流域降水量和气温统计降尺度成果

本研究降水量和气温统计降尺度数据来源于欧阳芬[16]的研究成果，对于修河流域历史时期(1961-2005年)的年平均降水量和气温模拟预估值与实测值采用各自的均值和标准差来进行对比，结果如图3、4所示。

从图3、4可知，研究区域历史时期(1961-2005年)多年月均降水量与多年月均气温的预测模拟值与实测值在大部分月份下均较为接近，但年内不同月份的数值波动较大，且降水量的拟合效果比气温相对更优。

图3 1961-2005年修河流域多年月平均降水量及其标准差的模拟值与实测值对比

图5给出了两种RCP典型浓度路径(RCP4.5、RCP8.5)下输出的40个GCM模式未来时期(2020-2099年)的年均降水量P和年均气温T的各模型预估结果，多模型平均系列如图6所示。

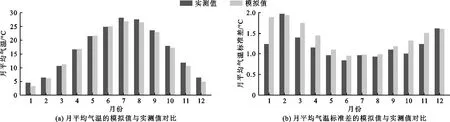
图4 1961-2005年修河流域多年月平均气温及其标准差的模拟值与实测值对比

通过对两种典型浓度路径下GCM模式输出的40种气候模式在(2020-2099年)未来时期降尺度的降水量和气温预估值比较分析，发现对于年均降水量，在两种RCP下均呈现微小的增大趋势(图5(a)、5(c))，而对于年均气温，在两种RCP下均呈现明显的上升趋势(图5(b)、5(d))。对于多模型平均系列而言，年均降水量和年均气温均呈现明显的上升趋势，2020-2100年RCP8.5下年均气温显著高于RCP4.5下年均气温(图6)。

图5 两种RCP典型浓度路径(RCP4.5、RCP8.5)下输出的40种气候模式的未来时期(2020-2099年)年平均降水量P和年平均气温T的各模型预估结果

图6 两种RCP典型浓度路径(RCP4.5、RCP8.5)下未来时期(2020-2099年)年均降水量P和年均气温T多模型平均值

3.3 基于ENE的非一致性设计洪水研究

即可得出某一特定重现期下非一致性设计值(本文仅给出重现期为1～50 a的情形)，如图7所示。

以重现期20和50 a为例，对图7中两种典型浓度路径在考虑和不考虑非一致性条件下的设计洪水流量结果进行分析：(1)虬津站各系列不考虑非一致性的设计洪水流量均远大于考虑非一致性的设计洪水流量。以Max 1d系列为例，当重现期为20 a时，一致性的设计洪水流量为7 394.8 m3/s，而RCP4.5和RCP8.5情景下非一致性设计洪水流量分别为4 981.3及4 505.9 m3/s；当重现期为50 a时，一致性的设计洪水流量为9 224.8 m3/s，相应的RCP4.5和RCP8.5情景下非一致性设计洪水流量分别为5 262.9及4 598.2 m3/s。虬津站其他时间尺度的设计洪水流量结果也有类似的规律，在选定的两种典型排放情景下，考虑非一致性的设计洪水流量均小于不考虑非一致性的设计洪水流量。(2)RCP4.5和RCP8.5情景下，各时间尺度20和50 a重现期非一致性设计洪水流量与一致性设计洪水流量相比分别减小13.5%～32.6%(平均约26.4%)和15.3%～39.1%(平均约31.0%)。(3)各重现期下，虬津站在RCP4.5排放情景下的设计洪水流量均较RCP8.5情景相应值更大，这与杜涛[11]在清江和西江流域的研究结果类似。(4)由于修河干流虬津站上游柘林水库对洪水的调节作用，虬津站考虑非一致性的设计洪水流量显著小于不考虑非一致性的设计洪水流量，这与相关研究[11,18]关于未来非一致性设计洪水流量显著高于不考虑非一致性条件下设计洪水流量的结果正好相反。

图7 基于ENE法的虬津水文站各系列非一致性和一致性条件下不同重现期的设计洪水值对比

4 结 论

本文以鄱阳湖修河干流虬津水文站多时间尺度洪水系列为例，将影响径流的气象因子作为非一致性洪水概率分布函数参数的协变量，在重现期期望超过次数(ENE) 概念下，推求对应某一目标重现期的非一致性设计洪水流量，主要结论如下：

(1)GA分布为模拟实测洪水流量QMax 1d、QMax 3d和QMax 1m的最优分布，LOGNO分布为模拟实测洪水流量QMax 7d和QMax 15d的最优分布，各时间尺度洪水流量系列位置参数均存在显著的非一致性。

(2)与一致性情形相比，以气象因子为协变量的最优非一致性统计模型拟合效果更佳，且两者设计洪水流量值存在显著差异。在选定的RCP4.5和RCP8.5两种典型排放情景下，后者设计洪水结果均小于前者设计洪水结果。

(3)本文应用GCM的降尺度数据时仍存在较大的不确定性，其中气温更为明显。同时，仅选取了RCP4.5和RCP8.5两种中、高排放情景下的GCM数据，下一步将重点考虑其他不同典型排放情景以及非一致性设计洪水流量的不确定性。