非对称河谷形态对面板堆石坝变形特性的影响

李和臻， 赵 然， 曾昭高， 陈辉弛*， 杨兴国， 周家文， 戚顺超

（1.四川大学水利水电学院，四川 成都 610065；2.中国水利水电第七工程局有限公司，四川 成都 610213）

混凝土面板堆石坝因具备的良好的地基适应性[1]、经济性等诸多优点成为世界上最有竞争力的坝型[2]，目前世界各地已建成的面板堆石坝大多数坐落在宽阔河谷中， 而在狭窄河谷上建造面板堆石坝的先例相对较少。 然而随着我国水利工程建设发展， 需在地形复杂、 山高坡陡的区域建设高坝，高面板堆石坝往往需要建造在狭窄河谷地带。对于建造在窄深河谷的高坝， 已有的研究成果表明[3-8]，狭窄河谷的面板坝坝体的应力和变形特征对于大坝整体结构的稳定及水库蓄水运行期间的安全性起到重要影响[9]。 研究不同河谷形态下坝体的应力变形规律， 并针对性的提出相应的工程应对措施， 给狭窄河谷上建设高面板堆石坝工程提供借鉴。

国内外不少学者都针对河谷形状对面板堆石坝的应力变形特性的影响进行了研究[10-15]。 程嵩[16]等采用三维有限元分析方法对大坝的应力应变以及位移在不同的河谷宽高比下进行计算， 发现大坝的应力应变以及位移受到河谷地形的影响明显。甘磊[17]等以玛尔挡水电站面板堆石坝工程为依托， 利用三维有限元分析的方法计算不同河谷坡度下面板堆石坝应力和位移的分布规律， 得出坝体沉降量与河谷坡度近似成线性关系， 且呈现出负相关关系； 第一主应力随河谷坡度的增加而减小，并发现在坡度>50°时坝体内开始出现应力拱效应，且随坡度增加应力拱效应越明显。 党发宁[18]等提出描述河谷形状的三个动态参数 （河谷宽度系数μ、河谷边坡陡缓系数δ 、河谷非对称系数γ），并采用这三个河谷形状参数研究河谷形状对面板堆石坝应力变形特性的影响。 狄文龙[4]等利用三维有限元计算分析并结合新提出的面板堆石坝拱效应评估参数，研究其对拱效应的影响，并探究河谷宽高比对坝体拱效应的影响情况。

本文以窄深河谷地区（V 型河谷）建设的某混凝土面板堆石坝为工程背景，建立了不同坡度、不同高度、 不同宽高比下非对称河谷混凝土面板堆石坝三维模型， 利用Plaxis 3D 软件对模型进行分析计算，研究坡度、高度、宽高比三种因素对非对称河谷上的面板堆石坝应力变形特性的耦合影响。

1 计算模型与参数

1.1 材料本构模型

虽然有很多中土体本构模型可以用来模拟岩土体的力学行为，但其适用性各有差异。 本文的应力变形计算主要考察堆石体应力变形特性。 假定河谷和地基的刚度很大， 河谷和地基中的变形可以忽略不计。 在PLAXIS 3D 软件中将河谷地基设成简化的线弹性模型，取其泊松比为0.2，杨氏模量E 为5.0GPa，具体参数见表1。

多个大坝的检测数据表明， 土体硬化模型所模拟的堆石体变形数据与后期坝体的实际监测数据拟合程度较高， 对于堆石体应力应变关系的研究采用Plaxis 3D 中土体硬化模型。

土体硬化模型主要包括以下本构参数，

主固结仪加载中的切线刚度：

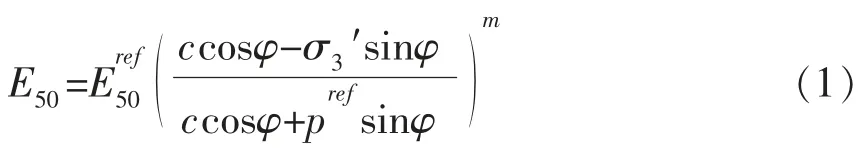
标准排水三轴试验中的割线刚度：

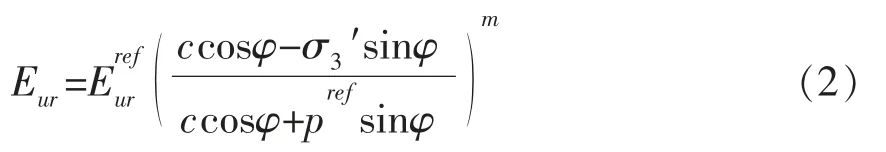
卸载重加载刚度：

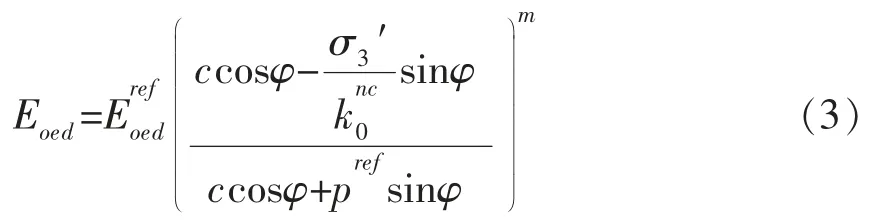
式中：σ3′为最小主应力；c、φ 为土体强度指标粘聚力、摩擦角；m 是一个幂指数，描述应力量级，土体较软，m 指数一般趋近于1，砂土和粉土一般取0.5 左右；pref为刚度参考应力， 在软件中默认设置为100KPa；为正常固结下的侧压应力系数，=1-sinφ。 所采用的模型材料参数结合已有研究和工程当地的材料特点取得， 堆石体的土体硬化模型所用的参数具体取值见表1。

表1 堆石体、 河谷地基模型材料参数表

1.2 计算模型

根据工程所在位置地形及本文研究需要，依托某面板堆石坝，对对称与不对称河谷形状下，不同坡度、 不同宽高比的河谷地基上的面板堆石坝进行三维应力变形有限元计算， 分别针对不同河谷形状参数（见表2）建立12 个三维有限元模型。在对称河谷与非对称河谷两种不同河谷形态下，分为坝高100m 和坝高200m，河谷底宽为20m，采用45°、55°、66°3 种不同坡度建立了6 个对称面板堆石坝三维有限元模型， 采用45°、55°和55°、66°以及45°、66°三种非对称坡度组合建立了6 个非对称对称面板堆石坝三维有限元模型。 根据工程的设计资料， 图1 给出某面板堆石坝的坝体剖面图。 计算坐标系采用笛卡尔坐标系，以河谷的纵向为Y 轴，横向为X 轴，坝高方向为Z 轴方向，河流的流向为Y 轴负方向， 三维有限元计算模型如图1。 图2 给出坝体的横纵剖面位置图。

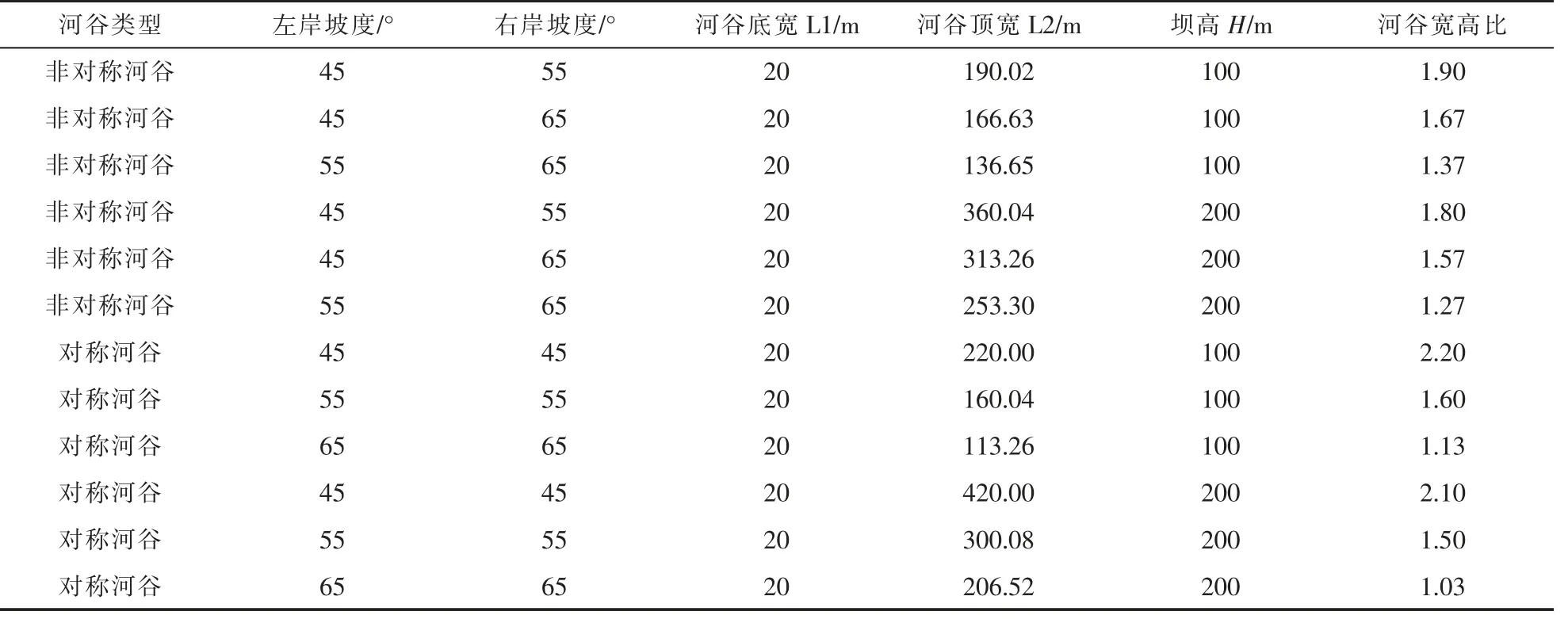
表2 河谷形状参数

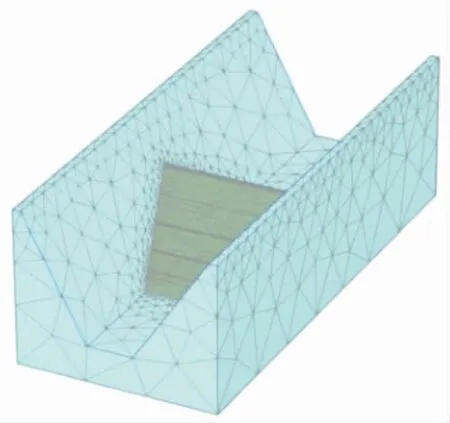
图1 三维有限元模型示意图

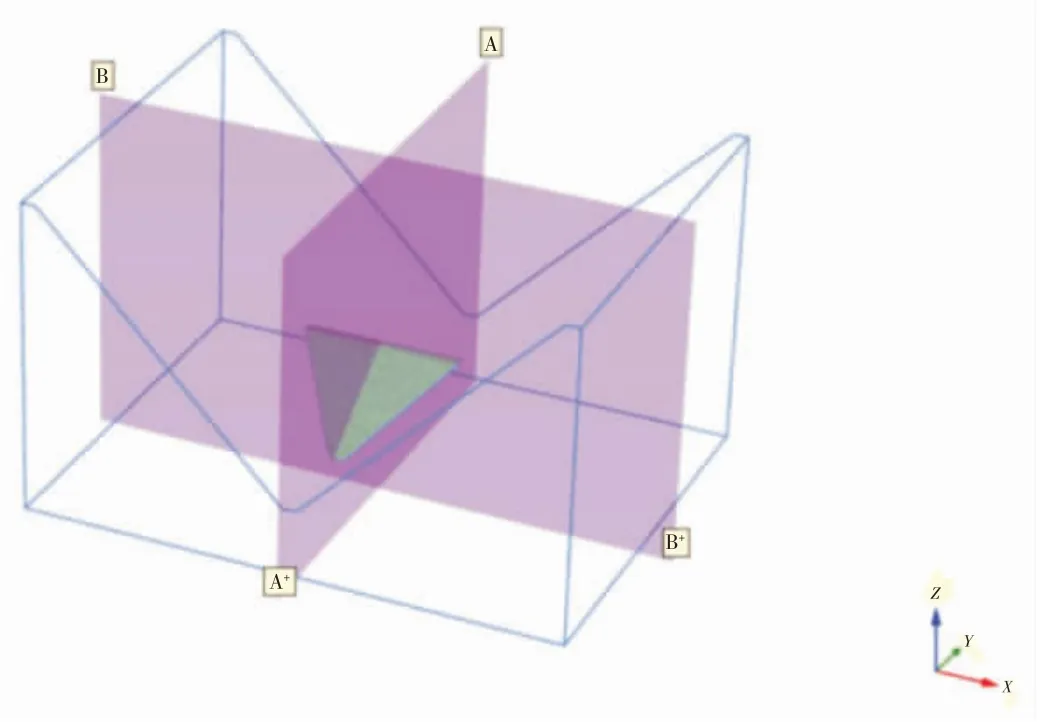
图2 横断面 （A-A）、 纵断面 （B-B） 位置图

图3 某面板堆石坝的坝体剖面图

2 河谷形状的影响分析

2.1 非对称河谷坡度的影响

图4 和图5 分别给出河谷坡度为45°、55°和55°、65°两种情况下堆石坝的应力变形分布情况，其中（a）图中正值表示拉应力、负值表示压应力；（b）图中正值表示与轴坐标正方向一致的位移、负值则相反。

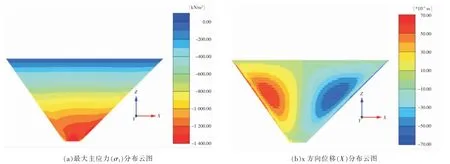
图4 45°、 55°非对称面板堆石坝 （100m） 应力位移计算结果

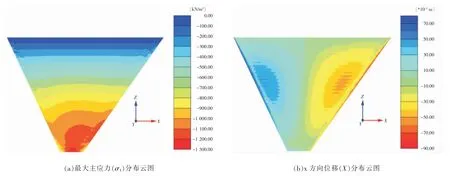
图5 55°、 65°非对称面板堆石坝 （100m） 应力位移计算结果

图（a）为堆石体大主应力分布云图，可以看出，堆石体分布云图的分布带基本呈现出水平向分布，大主应力的大小随深度逐渐增大，在坝底出现最大值且分布带呈现弯曲状， 且弯曲的程度随坡度增加而增大有成拱的趋势，随坡度增加，大主应力的最大值减小。

图（b）为堆石体x 方向位移分布云图即沿坝轴线方向位移云图，由于堆石体两岸边坡坡度不同，堆石体的非对称性使位移分布云图呈现出非对称的形态， 堆石体两侧位移呈现出向中间聚拢的趋势，这是因为坝体坝基对堆石体的约束作用，最大位移区域出现在坝高约1/2 位置处，且该值随坡度增加而增加； 堆石体沉降量分布形态随坡度的改变无明显变化，最大沉降量位于坝体中部区域处，且最大沉降量随坡度的增加而减小。 表3、表4 给出3 种不同坡度情况下， 堆石体大小主应力的最值、顺轴向位移的最值以及堆石体沉降量的最值。

表3 不同坡度坝体大小主应力最值表

表4 不同坡度坝体位移最值表

2.2 对称河谷坡度的影响

图6 和图7 分别给出河谷坡度为45°、55°的对称河谷下堆石体应力变形分布云图。 通过图（a）的对比分析可以发现， 非对称河谷与对称河谷面板堆石坝最大主应力分布形态相似， 在较缓的坡度下应力等值线成水平向分布， 随着坡度的增加等值线逐渐弯曲成拱， 与非对称河谷下的面板堆石坝相比， 对称情况下的应力拱效应显得更加明显；另外应力大小的变化情况两者也是相似的，随着坡度的增加而增大。

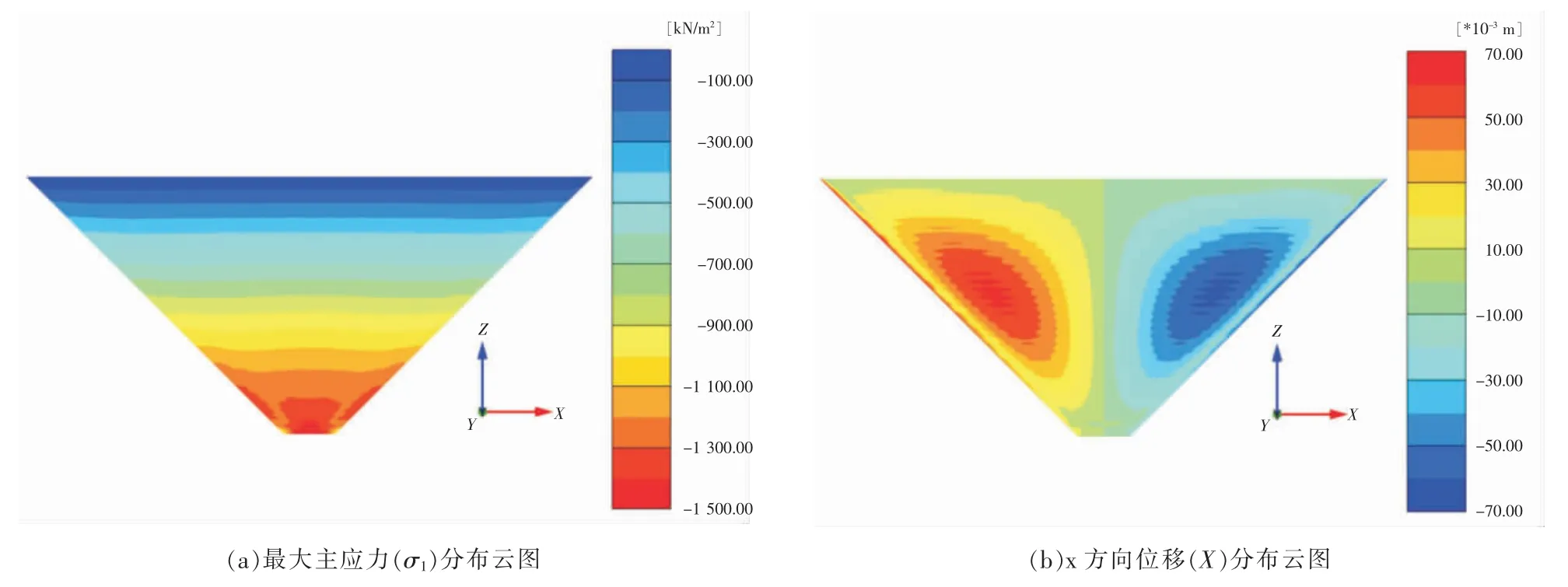
图6 45°对称面板堆石坝 （100m） 应力位移计算结果

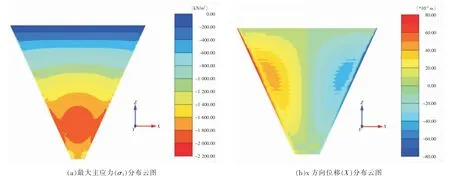
图7 65°对称面板堆石坝 （100m） 应力位移计算结果

图（b）为x 方向位移分布云图，从云图中可以明显看到一条分界线， 以分界线为界堆石体左右分别向里聚拢，并在两侧分别形成位移峰值区域；通过对比分析，随着河谷坡度增加x 方向位移数值也在增大，且位移均表现为向里聚拢；坝体沉降量分布形态与非对称河谷下坝体沉降量相似， 且形态不随坡度变化而改变， 沉降量由坝体表面向坝体内部逐渐递增， 在坝体表面沉降量较小几乎不发生沉降，最大沉降量发生在坝体中部；沉降量的大小则随坡度的增加而减小， 这是河谷坡度的增加使坝体两岸坝基河谷对坝体的竖向位移约束增强而导致的。

2.3 河谷宽高比的影响

据不完全统计， 中国目前在建及已建面板堆石 坝 数 量 超300 座[1，19，20]，随 着 大 坝 建 设 重 心 日 益向我国西部转移， 在狭窄河谷这样的特殊地形上进行面板堆石坝的建设的挑战将进一步引起人们重视。 一些学者[8，21，22]提出采用河谷宽高比（坝顶最高处河谷宽度/最大坝高） 来定量描述河谷的宽窄程度， 该方法得到大家一致认同且得到广泛的应用， 本文也将采用该指标用以标定河谷的相对宽窄程度。截止2014 年，我国已建及在建100m 以上面板堆石坝中河谷宽高比在2.5 以下数量约占30%，狭窄河谷上建设面板堆石坝的数量占不小的比例， 因而本文拟采用河谷宽高比在1—2.5 之间共12 种不同的河谷宽高比（表2）进行应力变形有限元计算。 图8—13 给出了面板堆石坝不同宽高比下坝体第一、 第三主应力及坝体位移的变化曲线图。

宽高比对面板堆石坝最小第一主应力的影响近似于线性变化， 压应力峰值大小随宽高比增大而增大， 100m 坝高情况下对称与非对称面板堆石坝最小第一主应力随宽高比变化的曲线几乎重合，而在200m 坝高情况下非对称面板堆石坝较对称坝体对应曲线整体向下移动。 这意味着在100m坝高的情况下， 非对称性对最小第一主应力的影响较小，而在200m 坝高的情况下，关注最小第一主应力则应注意非对称性对其的影响， 非对称坝体应力水平相对较高（图8）；河谷宽高比的变化引起的最大第一主应力的变化规律较为复杂， 同一坝高情况下， 对称与非对称坝体所对应曲线形状有较大差异。 100m 坝高所对应的两条曲线总体上是随宽高比的减小呈现增大的趋势，而在200m 坝高所对应曲线中， 非对称坝体所对应曲线呈现出最大第一主应力随宽高比的减小呈现减小并有趋向于正值的趋势，即可能出现拉应力。 进一步说明在200m 坝高情况下，应注意非对称性对第一主应力的影响（图9）。

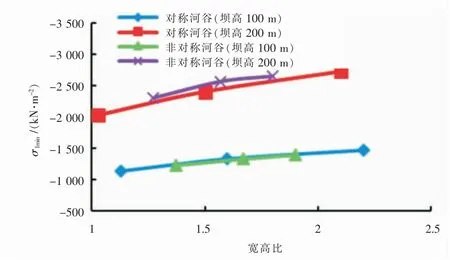
图8 宽高比对坝体最小第一主应力的影响

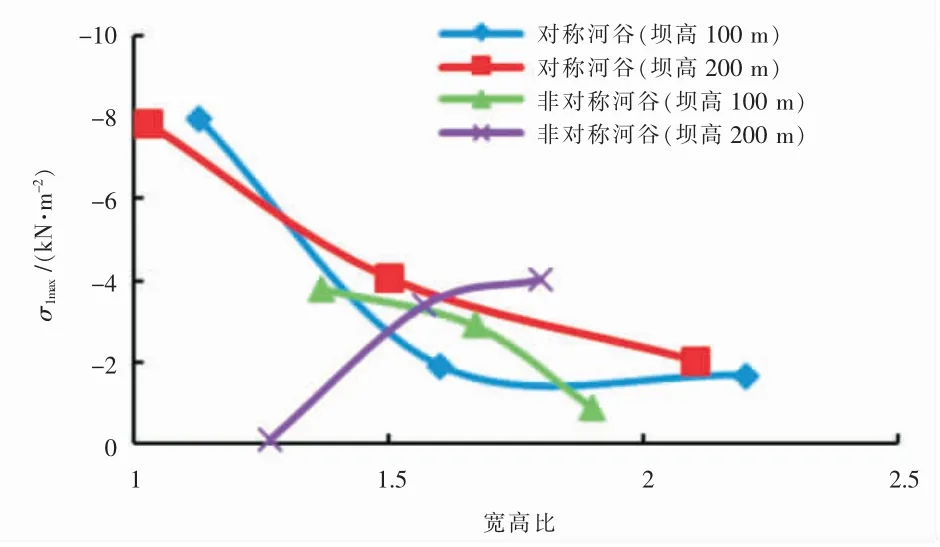
图9 宽高比对坝体最大第一主应力的影响

最大第三主应力为拉应力， 其值随河谷宽高比的减小而增大， 最大第三主应力产生的拉应力主要分布在坝肩， 在非对称坝体中拉应力分布范围陡坡较陡坡更大一些（图5）。且由于坝体的非对称性拉应力的最大值向陡坡方向偏移， 这就符合（图10）曲线中非对称坝体最大第三主应力曲线高于对称坝体的现象。 因而可以推断，在非对称河谷上修建较小宽高比的面板堆石坝可能会出现较大拉应力，从而增大坝肩出现裂缝的可能性。 最小第三主应力随河谷宽高比减小而减小， 且不同坝高下对称于非对称坝体曲线接近重合， 非对称性对面板堆石坝最小第三主应力的影响较小，受坝高、宽高比等因素影响较大（图11）。

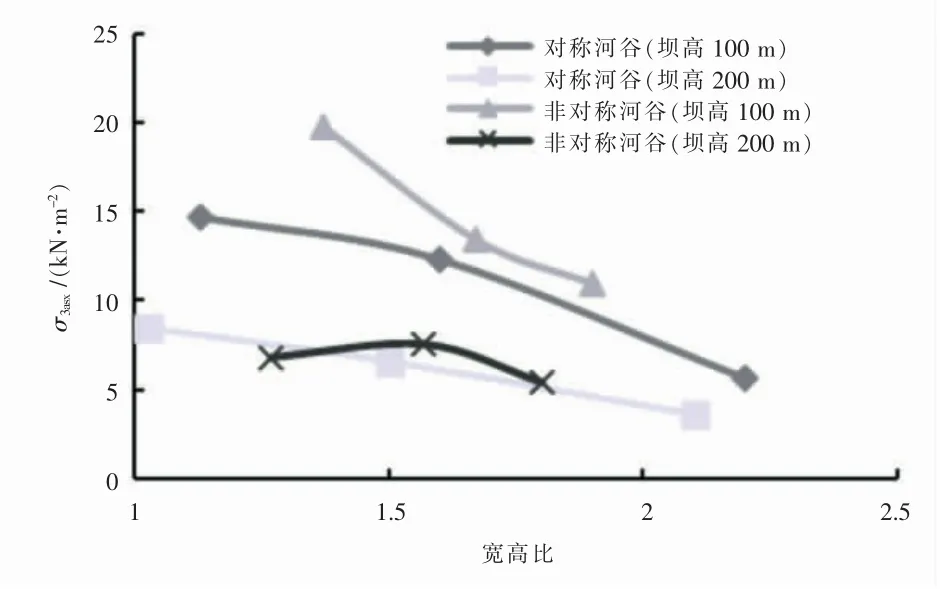
图10 宽高比对坝体最大第三主应力的影响

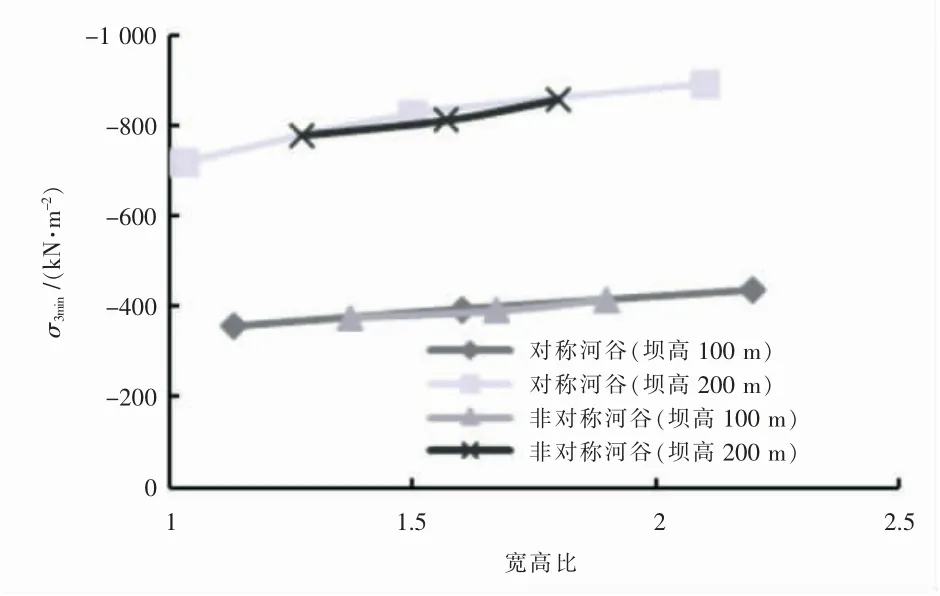
图11 宽高比对坝体最小第三主应力的影响

最大坝轴向位移随坝体宽高比变化曲线在宽高比与坝高的共同影响下，不同坝高情况下，宽高比对最大坝轴向位移的影响有较大差异。 坝高100m 的情况下，最大坝轴向位移随宽高比减小而增大；坝高200m 情况下，最大坝轴向位移随宽高比减小而减小， 两种完全相反的变化趋势说明坝高对最大坝轴向位移的影响较大。 可以推断在坝高较高的情况下，随着宽高比减小，坝基对坝体两侧的约束逐渐加强。 另外，在宽高比大于1.5 的情况下，对称坝体与非对称坝体所得曲线接近重合，对称性对最大坝轴向位移影响不大。 而在宽高比小于1.5 时，曲线出现的非重合部分，坝体非对称性的影响开始出现， 非对称坝体最大坝轴向位移要略高于对称坝体（图12）；最大沉降量随河谷宽高比减小而减小，且100m 坝高的面板堆石坝最大沉降量随宽高比变化速率较200m 坝高坝体小，故而说明坝高越高、河谷宽高比小，坝基及堆石坝两岸边坡对坝体约束能力越强， 对坝体的沉降变形影响越大。 非对称坝体与对称坝体的变化曲线重合， 可以推断坝体的非对称性对坝体的最大沉降量值影响较小（图13），但应注意非对称坝体发生最大沉降量的部位往往不在坝轴线上， 沉降量较大的区域通常稍偏向于坡度较缓的边坡。 这样的沉降量偏移现象容易引起坝体修筑及运行期间的不均匀沉降， 通过施工中采取适当分区调整碾压参数的方法， 调整坝体两岸及中心之间的沉降差避免较大的不均匀沉降。

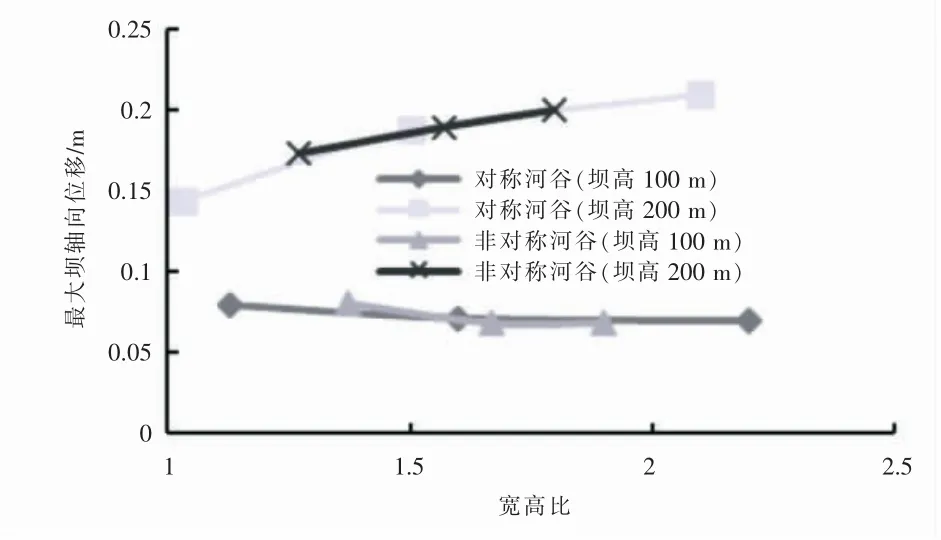
图12 宽高比对最大坝轴向位移的影响

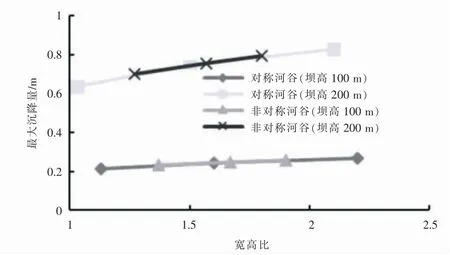
图13 宽高比对坝体最大沉降量的影响

3 结论

本文采用Plaxis 3D 有限元分析软件， 建立了窄深河谷中面板坝堆石体的三维有限元模型。 利用三维非线性有限元分析方法， 对不同河谷形态（不同河谷坡度、不同宽高比、不同对称性）下的面板堆石坝进行数值模拟。 根据所得面板堆石坝应力变形结果， 重点分析不同的河谷形态耦合作用下堆石坝体应力变形的分布规律， 得出主要结论如下：

（1）在本文的研究范围内，坡度对面板堆石坝应力变形的分布形态影响较小， 但坝体内各应力变形量均受到坡度变化的不同程度的影响； 随坡度的增加坝体中大小主应力的最值及坝体沉降量均减小， 坝体顺坝轴向位移则随坡度的增加而增大。

（2） 面板堆石坝的非对称性使得坝体内沿坝轴线方向的纵剖面上的应力变形的分布形态呈现出非对称性；大主应力、顺坝轴向位移分布形态均向陡坡偏移，易造成坝体不均匀沉降。

（3）随河谷宽高比减小，坝体内最小第一主应力，最小第三主应力，最大沉降量均减小。 最大沉降量随宽高比的变化速率受坝体非对称性影响较小，最小第一主应力在坝高200m 时随宽高比的变化速率受坝体非对称性影响较大。

（4） 坝体最大轴向位移随河谷宽高比的变化趋势与坝体高度有关。在100m 坝高时最大轴向位移随宽高比减小而增大，在200m 坝高时最大坝轴向位移随宽高比减小而减小； 非对称性对其随宽高比变化速率的影响仅在宽高比小于1.5 后出现，非对称坝体最大轴向位移随宽高比变化速率在宽高比小于1.5 明显加快，在宽高比大于1.5 时与对称坝体变化速率一致。 □