基于FPA-ELM模型的中长期径流预测——以雅砻江流域为例

洪 敏，艾 萍，2，岳 兆 新

(1.河海大学 水文水资源学院，江苏 南京 210098； 2.河海大学 计算机与信息学院，江苏 南京 211100； 3.南京工业职业技术大学 计算机与软件学院，江苏 南京 210023)

0 引 言

流域水文系统是一个复杂的动态系统，影响中长期径流过程变化的水文要素具有复杂的时空变异性。目前还没有一个通用、完善的预测模型可适用于所有情况及地区的中长期径流预测，且预测模型中的智能算法选择也在很大程度上影响中长期径流预测效果。一直以来，以BP神经网络(Backpropagation Neural Networks，BPNN)为代表的智能算法广泛应用于径流预测领域[1-3]，但在训练过程中，模型参数难以准确确定，因而整体预测效果欠佳。相比上述模型，极限学习机[4-5](Extreme Learning Machine，ELM)具有模型结构简单、通用性好、计算速度快等优点，被广泛应用于干旱、水文预报等诸多领域。但该模型的参数选取具有随机性，导致模型的鲁棒性不强，尤其是部分隐含层节点在实际应用中可能无效[6]。Yang[7]受自然界中花朵授粉行为启发，提出了花授粉算法(Flower Pollination Algorithm，FPA)。该算法具有结构简单、控制参数少、鲁棒性强及计算效率高等优点[8]。相比于遗传算法(Genetic Algorithm,GA)和粒子群(Particle Swarm Optimization，PSO)等生物启发式算法，FPA不仅具有较强的收敛速度和寻优能力，而且在收敛精度和搜索能力等方面更有优势[9]。

因此，本文提出了一种花授粉算法优化极限学习机模型的中长期径流预测方法(FPA-ELM)，并应用于雅砻江流域中长期径流预测中。通过与BPNN、支持向量机(Support Vector Machine，SVM)、ELM和GA-ELM等数据驱动模型进行比较分析，验证了本文所提算法具有更好的预测效果，可为基于智能算法的中长期径流变化趋势预测提供借鉴。

1 研究方法

本文以中长期径流预测分析为目标，主要分为数据组织、因子筛选、预测模型构建和结果评价4个方面。数据组织主要包括流域径流整体趋势变化因子构造和气候及降雨数据处理；因子筛选是通过信息熵方法计算得到影响径流的显著因子集合；预测模型为花授粉算法优化极限学习机模型，构建FPA-ELM模型，完成中长期径流预测；模型评估是选用水文预报领域常用的评价指标，综合评价预测模型的性能。

1.1 流域径流整体趋势变化因子构造

模型的输入数据主要包括两个来源：① 基于流域地形与站点空间分布的位置特征，构建能够反映流域径流整体趋势变化的综合因子；② 影响流域径流产生的降雨数据与气候相关数据。

依据粒计算理论，以水文站点的流域控制面积占比为权重乘以每个站点的月平均径流量，构造流域径流整体趋势变化因子(Comprehensive Runoff Index，COM)，用以描述流域径流的情势变化。流域径流整体趋势变化因子构造方法如下[10-11]：

(1)

(2)

式中：Wi为第i个水文站点的权重；Qi为第i个水文站点的控制面积百分比；m为流域内月均径流一致性较好的水文站点个数；Cj为第j个月的径流趋势变化因子；Cij为第i个水文站点第j个月的月均径流量。

1.2 基于信息熵的因子筛选

1.2.1偏互信息原理

当前，影响径流过程变化的关键因子的筛选方法主要包括相关系数法、先验知识法、信息熵法及主成分分析法[12-14]，且每种方法都有各自适用的领域范围。其中，偏互信息法是基于信息熵的因子筛选方法，适用于备选因子间的线性和非线性相关关系。相较于上述几个常用的因子筛选方法，偏互信息法具有减少变量的冗余度、提高因子的筛选速度等优点，因此更适用于中长期径流过程变化的因子选择。

偏互信息计算方法如下：

(3)

x′=x-E[x|z]

(4)

y′=y-E[y|z]

(5)

式中：PMI为偏互信息；fX′，Y′(x′，y′)为变量X′与Y′的联合概率密度函数；fX′(x′)为X′的边缘概率密度函数；fY′(y′)为Y′的边缘概率密度函数；E表示数学期望值；x表示输入变量；y表示预测对象；z表示已入选的输入变量集合。

偏互信息离散计算方法如下：

(6)

式中：N为离散样本个数；i为观测样本编号；fX′，Y′(xi′，yi′)为(xi′，yi′)处的联合概率密度估计；fX′(xi′)为xi′处的边缘概率密度估计；fY′(yi′)为yi′处的边缘概率密度估计。

1.2.2基于PMI的变量选择步骤

当输入变量有多个时，由于多个变量之间可能存在某种相关关系，例如X，Z为输入变量，Y为输出变量，则输入变量X与Z之间可能存在相关关系，则互信息I(Y，Z)的值可能会大于实际值。因此，本文基于条件期望方法将变量Y和Z中包含的有关X信息剔除，变量间的相关度通过偏互信息PMI来度量。剔除X后，Y记为u，Z记为v，具体定义为

(7)

u=Y-mY(x)

(8)

v=Z-mZ(x)

(9)

Y和Z之间的偏互信息转化为

PMI(Z，Y)=I(v，u)

(10)

假设C为输入变量集，Y为输出变量，S为预测模型的关键输入变量集合，Cs为候选变量，对应PMI值最大时的输入变量集合，那么基于PMI的变量筛选步骤如下：

(1) 初始化S，且S为空集；

(2) 如果C是空集，返回步骤(1)；

(3) 计算u=Y-mY(S)；

(4) 对于Cj∈C的每个元素，计算v=Cj-mCj(S)；

(5) 如果I(v，u)最大时，选取候选变量Cs；

(6) 计算赤池信息准则AIC值，如果AIC值降低，则将Cs移到最优输入变量集为S，返回步骤(2)；若AIC值增大则终止筛选。

AIC计算公式如下：

(11)

式中：ui为根据已选变量计算的Y回归残差；p为已选变量个数；n为采样个数。

AIC值随着自变量的筛选不断减小，当AIC为最小时，最优自变量集合筛选完毕。

1.3 FPA-ELM径流预测模型构建

1.3.1极限学习机

假设任意给定N个不同样本(Xi，ti)。其中，Xi=[xi1，xi2，…，xin]T∈Rn，ti=[ti1，ti2，…，tim]T∈Rm，目标函数定义如下[4]：

(12)

式中：N为样本总量；g(x)为激活函数；Wi为输入层与隐含层的权重矩阵，且Wi=[wi1，wi2，…，win]T；βi为隐含层与输出层之间的权重矩阵，且βi=[βi1，βi2，…，βim]T；bi为第i个隐含层神经元的偏置；oj为第j个样本的网络输出值；Wi·Xj为Wi和Xj的内积；C为隐含层神经元个数。

预测值与真实值误差最小，可表示为

(13)

即存在βi，bi，Wi使得：

(14)

用矩阵表示为

Hβ=T

(15)

(16)

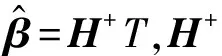
1.3.2结合K折交叉验证与花授粉算法的ELM参数优化

花授粉算法(FPA)是基于花粉传播的自然过程，依靠其他生物体的携带，彼此之间形成一种合作共生关系[15]。FPA由概率常数调节全局搜索和局部搜索之间的转换，且概率常数取值范围为0～1。FPA算法流程如图1所示，具体算法如下：

(1) 全局搜索的数学定义为

(17)

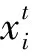
(2) 局部搜索的数学定义为

(18)

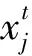
本文以上述花授粉算法为基础，提出结合K折交叉验证(K-fold Cross Validation，K-CV)与花授粉算法优化极限学习机模型参数的方法(算法流程如图2所示)，包括以下几个部分：

(1) 参数初始化。假设训练样本为[xi，yi](xi∈Rn，n为极限学习机模型的输入神经元数量，i=1，2，…，N，N为总样本数量)，构造极限学习机的激励函数以及设置隐含层节点数量，其中C为隐含层节点个数，g为极限学习机模型的迭代次数。

(2) 构造极限学习机模型的适应度函数。以K-CV的均方根误差(RMSE)作为极限学习机模型的适应度，寻找平均RMSE最小的个体。

(3) 迭代更新。计算极限学习机模型的适应度大小，并据此更新个体。

(4) 极限学习机模型最优参数生成。判断是否达到预先设定的算法终止要求，如果达到，则获得极限学习机模型的最优参数组合；否则，回到步骤(2)。

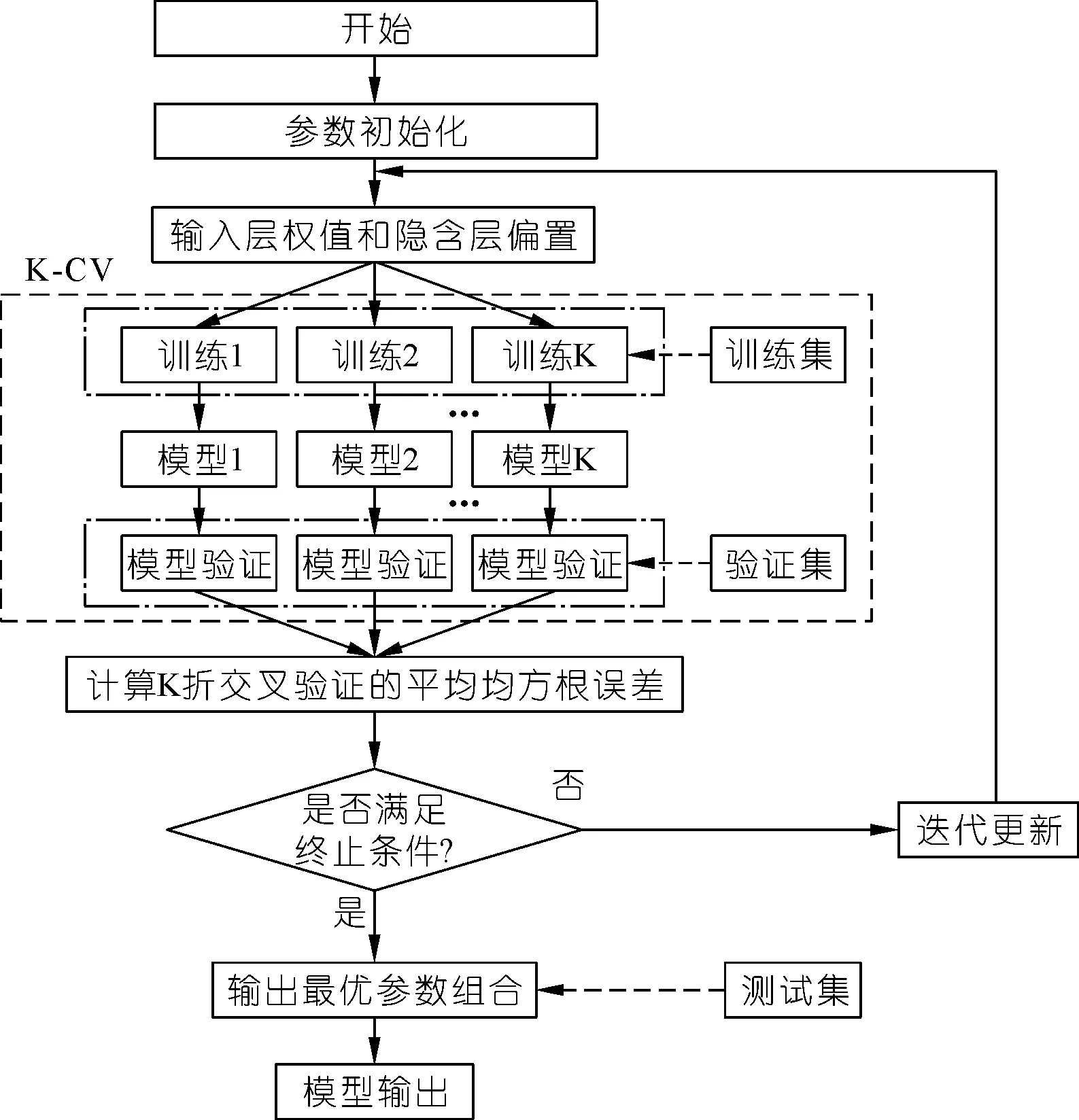
图2 FPA-ELM模型流程Fig.2 Flowchart of the FPA-ELM model

1.4 评价指标

模型预测性能评价通过选用水文预报中常用的5个指标：平均绝对百分比误差(Emape)、均方根误差(Ermse)、确定性系数(Edc)、合格率(Eqr)及运算时间(T)等，具体计算见文献[10]。

2 实例分析

2.1 研究区概况与数据资料

雅砻江流域位于青藏高原东部，流域地形落差大、水量丰沛，水资源丰富，因此开展中长期径流预测具有十分重要的现实意义和应用价值。雅砻江流域及其站点分布如图3所示。

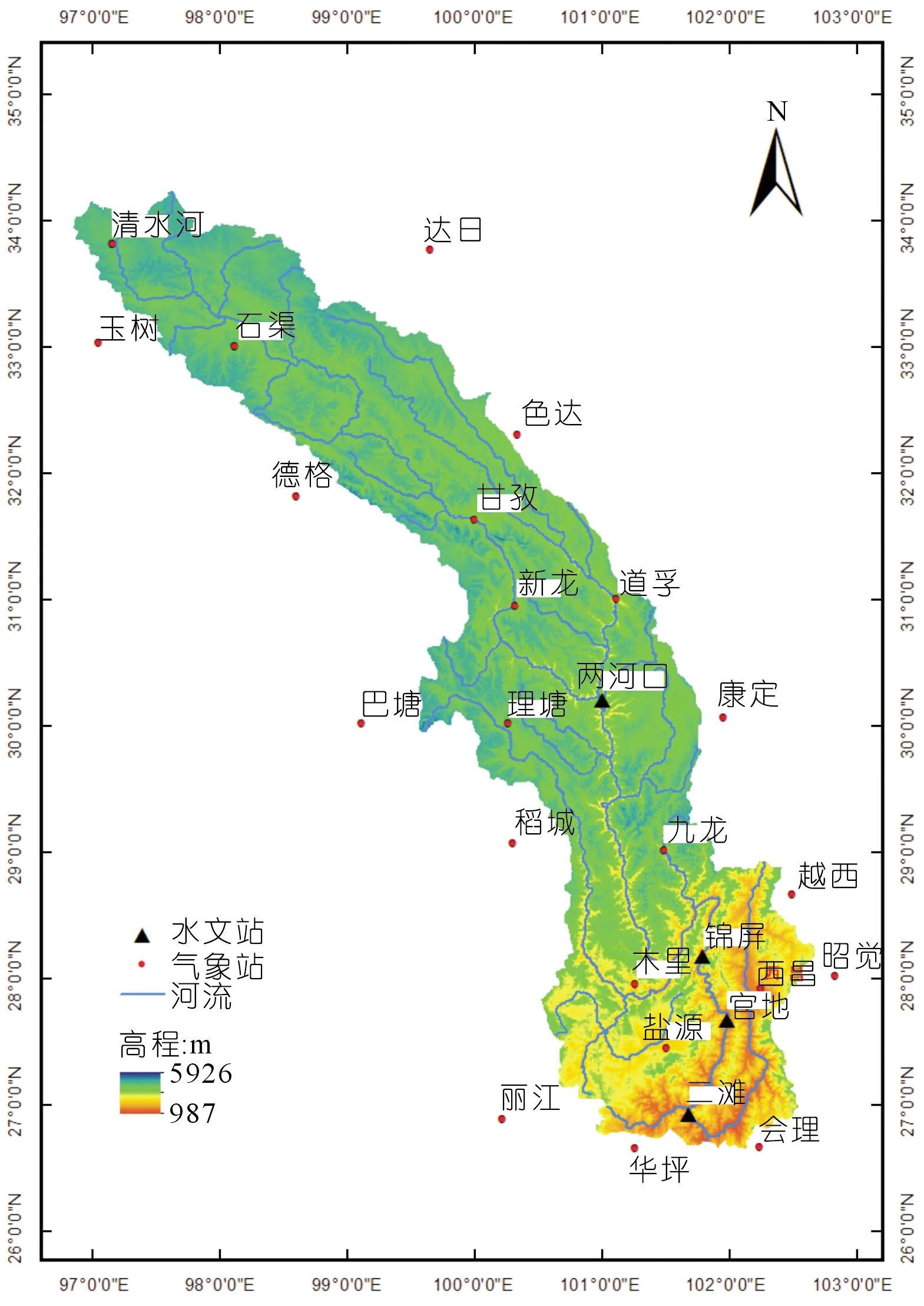
图3 雅砻江流域及其站点分布Fig.3 Yalong River Basin and its stations

本文的试验数据包括前期月径流整体趋势变化因子、气候、降水等624组数据，时间为1960年1月至2011年12月。具体包括两河口、锦屏、官地和二滩等4个水文站的径流数据、22个气象站的降雨数据以及相关气候数据。其中具体的气候数据如表1所列。

2.2 流域径流整体趋势变化因子构造

选取两河口、锦屏、官地和二滩4个水文站点的流域控制面积占比，根据公式(1)和(2)计算每个水文站点的权重值(见表2)，再以权重值分别乘以各自站点的月平均径流量(细粒度)，最终求和得到流域径流整体趋势变化因子(粗粒度)构造。

表1 相关气候数据Tab.1 Related climate data

表2 基于测站控制面积的流域径流整体趋势变化因子 构建权重Tab.2 Construction of weight of Comprehensive Runoff Index of watershed runoff based on the area controlled by stations

2.3 基于偏互信息法的关键特征因子筛选

雅砻江流域中长期径流预测的主要特征因子包括：径流整体趋势变化因子fcom(fcom(t-1)，…，fcom(t-11)，fcom(t-12))；降雨因子fr(fr(t-1)，…，fr(t-11)，fr(t-12))；气候因子fc1(fc1(t-1)，…，fc1(t-11)，fc1(t-12))，fc2(fc2(t-1)，…，fc2(t-11)，fc2(t-12))，…，fc21(fc21(t-1)，…，fc21(t-11)，fc21(t-12))，共计23×12=276个。

本文在偏互信息方法基础上，结合了人工筛选，获得预测模型的关键特征因子集，具体流程如下：

(1) 基于PMI方法计算相关性排名前20的备选因子(见表3)。

表3 基于PMI方法的备选因子相关性大小(排名前20)Tab.3 Correlation of candidate factors based on PMI method(top 20)

(2) 以上述结果为基础，通过人工挑选方式分别从径流整体趋势变化因子、降雨因子和气候因子三类对象中选取排序前5的关键特征因子集合，形成预测模型的最终特征因子输入，共计13个：径流整体趋势变化因子fcom(t-12)，fcom(t-1)，fcom(t-11)，fcom(t-2)，fcom(t-3)；降雨因子fr(t-1)，fr(t-7)，fr(t-12)；气候因子fc1(t-1)，fc15(t-6)，fc3(t-7)，fc13(t-8)，fc16(t-1)。

2.4 基于FPA-ELM模型的月径流预测

2.4.1数据集划分

基于FPA-ELM模型的月径流预测数据集划分为两个部分(7折交叉验证和模型测试)。其中，用于7-CV的数据为1960年1月至2001年12月共504组样本数据(随机选取6组用于训练，余下1组用于验证模型)，测试期2002年1月至2011年12月共120组样本数据。

2.4.2参数设置

不同算法的参数初始化设置如下：

(1) FPA：种群大小为90，最大迭代次数为600，常数P为0.8，γ为1，λ为1.5，适应度函数采用K-CV的平均RMSE，极限学习机模型的激活函数选择“sigmoid”函数。

(2) GA：种群大小、适应度函数及ELM的激活函数类似FPA，最大遗传代数设置为600，交叉概率为0.7，变异概率为0.01。

(3) BPNN采用7-CV方法，且结构与极限学习机模型一致，BPNN模型的训练函数采用“tansig”函数，学习函数采用“logsig”函数，最大训练次数设置为1 000，学习速率设置为0.1，训练算法采用LM(Levenberg-Marquardt)算法，动量因子大小设置为0.9，模型的期望误差设置为0.001。

(4) SVM模型采用RBF(Radial Basis Function)核函数，其中σ=0.5，惩罚参数C=1，ε=0.001。

2.4.3预测结果及对比分析

FPA-ELM与BPNN，SVM，ELM和GA-ELM等4种对比模型的交叉验证期和测试期的性能对比如表4所列。不同模型的预测结果对比如图4所示，预测值和观测值及确定性系数Edc对比如图5所示。

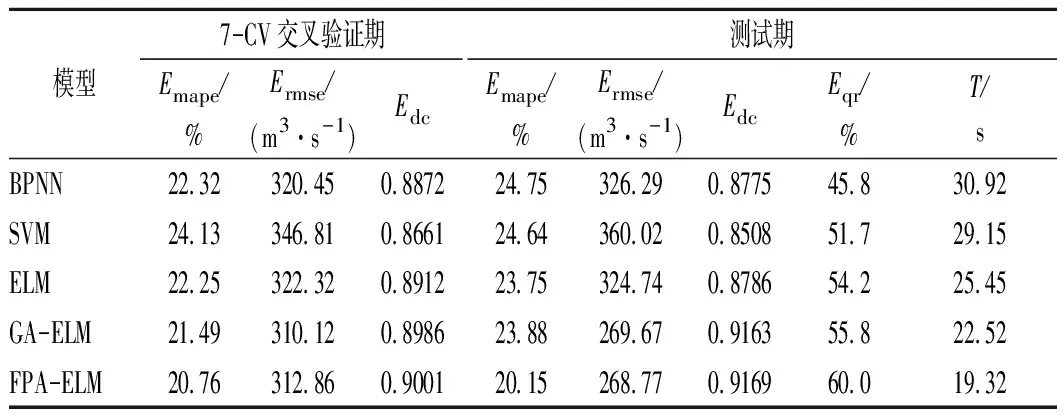
表4 不同模型在交叉验证期和测试期的性能比较Tab.4 Performance comparison of different models in cross validation period and test period

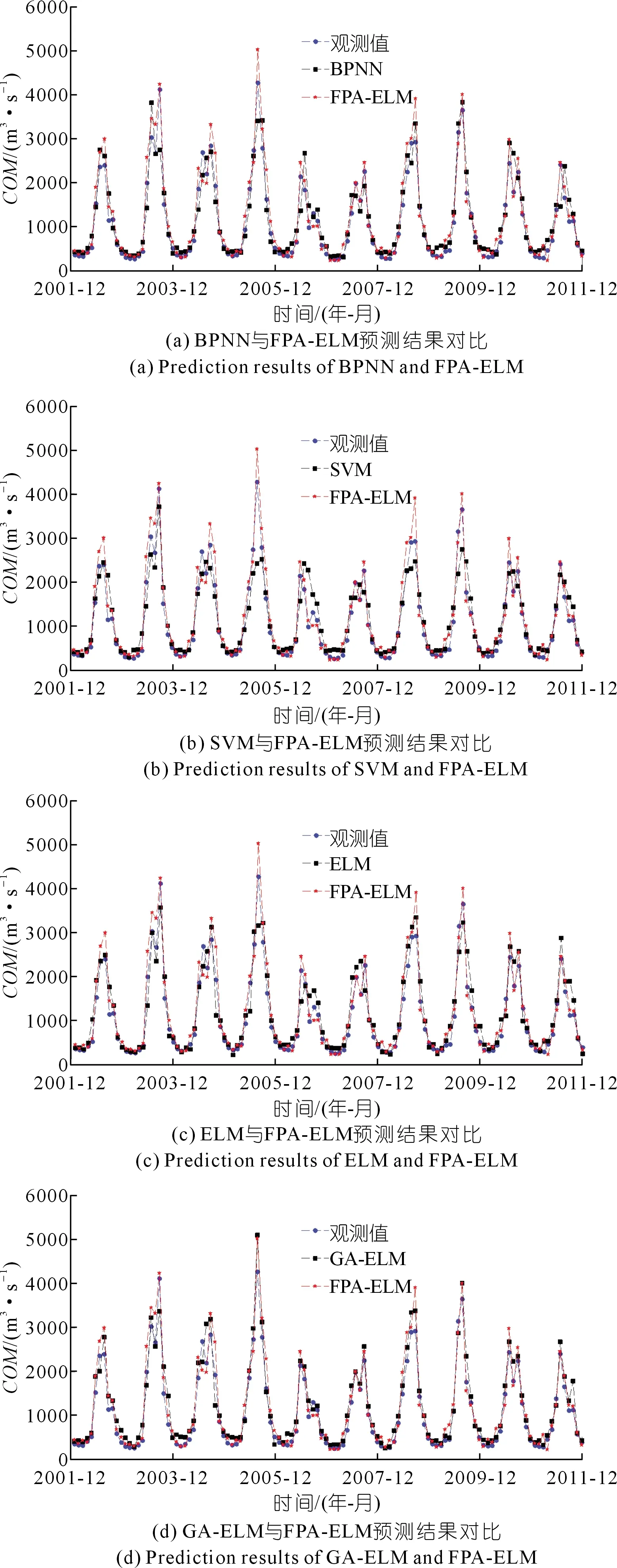
图4 不同模型的预测结果对比Fig.4 Comparison of prediction results of different models

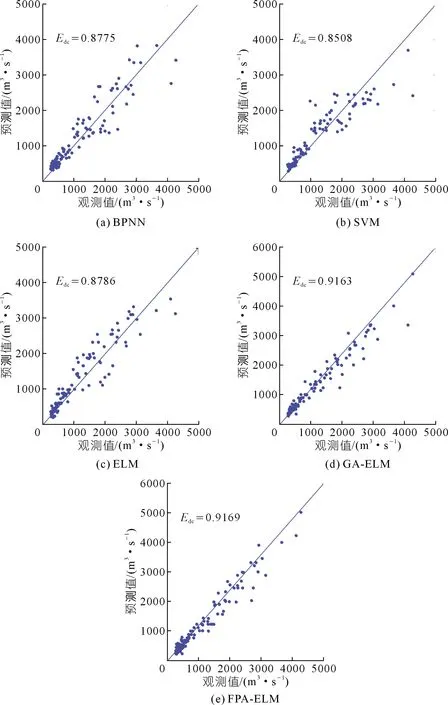
图5 不同模型的预测值和观测值对比Fig.5 Comparison on observed and predicted values of different models

上述试验结果表明：5种数据驱动预测模型均具有较好的预测效果，其中生物启发式算法优化极限学习机模型在Emape，Ermse和Edc这几个指标中整体上优于另外3种模型，特别是FPA-ELM模型的性能最优，验证了本文所提算法的优越性。其中：在Emape评价指标中，FPA-ELM模型效果最好，BPNN和SVM效果较差；在Ermse评价指标中，GA-ELM和FPA-ELM模型较小，SVM模型较大；在Edc评价指标中，5种数据驱动模型的确定系数都超过了0.85，显示了基于信息熵因子筛选方法的优势，其中FPA-ELM模型在该项指标方面表现最佳；在Eqr评价指标中，尽管FPA-ELM模型可以应用于水文作业，但5种预测模型的整体合格率较低，其主要原因在于月径流预测的预见期较长且影响中长期径流预测的主要对象及其特征因子较多，导致预测的不确定性提高，因而影响整体的中长期径流预报合格率；在运算速度评价中，FPA-ELM和GA-ELM两种生物启发式模型明显优于其他3种模型，其中FPA-ELM模型表现最佳。

综上所述，相比其他4种常用的数据驱动模型，本文所提出的花授粉算法优化极限学习机模型(FPA-ELM)在中长期径流预测方面更有优势。主要原因在于相较于传统的非线性预测模型(BPNN，SVM)，ELM具有模型结构简单、通用性好、计算速度快等优点。此外，本文结合K折交叉验证与花授粉算法，克服了传统ELM的不足，且相比于GA算法，FPA具有较强的收敛速度和寻优能力，能够快速搜索ELM的最优参数，因而整体预测效果较好。

3 结 论

(1) 构造了反映流域水情丰枯变化的流域径流整体趋势变化因子(COM)，并采用偏互信息法获得了影响中长期径流过程变化的关键因子集，形成中长期径流预测模型的关键特征因子输入。

(2) 相较于BPNN，SVM，ELM和GA-ELM等数据驱动模型，结合K折交叉验证与花授粉算法优化ELM参数构建的FPA-ELM模型，在Emape，Ermse，Edc，Eqr和运算时间等性能评价指标方面整体上优于上述4种预测模型，具有更好的预测效果，可为基于智能算法的中长期径流预测提供借鉴。