软土基坑开挖对临近既有隧道变形影响研究

韦 宗 科，陈 健，3，，5，陈 斌，黄 珏 皓，3，

(1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071； 2.中国科学院大学，北京 100049； 3.湖北省环境岩土工程重点实验室，湖北 武汉 430071； 4.岩土力学与工程国家重点实验室宁波工程学院工程软土实验中心，浙江 宁波 315211； 5.中国-巴基斯坦地球科学研究中心，北京 100049)

0 引 言

盾构隧道的变形和不均匀沉降严重影响隧道结构性能，危害隧道的正常使用和运行，降低行车舒适性和安全性，甚至引发地铁安全运营事故，造成严重后果。宁波市地处滨海平原，广泛分布着深厚海相沉积的淤泥质软黏土。宁波市地铁地下结构位于软土地层中，盾构法隧道是宁波市软土地铁隧道的主要型式。宁波市地铁1号线一期工程于2009年6月正式开工建设，2014年5月投入运营。该盾构隧道自开通运营以来，部分区间伴随着隧道变形的发展，多处管片出现了接缝渗水、大面积掉块、裂缝和破损、起皮劣化等不良现象，在2017年2月至2018年2月甚至发生局部过大变形，若不采取相关保护措施，势必引起严重的安全事故。

引起软土盾构隧道变形的因素众多，既有盾构隧道施工期的，也有运营期的，既有系统自身的，又有周边环境的，软土盾构隧道不均匀沉降是多种因素共同作用的结果。客观上来讲，最直接和最主要的影响因素是隧道周边软土变形。软土孔隙比高、压缩性强、抗剪强度低，在地铁施工过程中，隧道周边软土往往会产生较大变形。在地铁隧道运营过程中，由于地面卸载以及附近新建地下工程开挖等周边环境作用，盾构隧道周边软土的变形和位移会进一步发展[1-3]。

近年来许多学者对这个问题进行了研究，大多采用数值模拟与实测结果相结合的方法[4-8]。刘国彬等[6]采用理论分析的方法，研究时空效应对基坑工程隆起的影响，提出了时间、开挖宽度影响系数，提出隧道因受临近基坑施工影响而产生的位移变形计算方法。高广运等[7]采用数值模拟的方法，运用FLAC3D软件建立三维数值分析模型，模拟分析上海市某临近地铁隧道的基坑工程，对基坑施工整个过程进行动态模拟。邹伟彪等[8]采用数值模拟与现场实测的方法，运用数值模型对实际施工工况进行模拟，分析临近开挖卸荷对既有隧道的影响，着重研究隧道变形特征。郑刚[9-10]等采用数值模拟的方法，结合现场实测数据，采用ABAQUS软件模拟基坑施工过程，并分析临近既有隧道箱体两侧土体的影响效应。冯龙飞[11]采用数值模拟的方法，由有限元分析方法分析侧方基坑开挖对盾构隧道的影响，重点研究隧道的变形情况，并研究了有效监测与处理地铁隧道变形的措施以及应用。杨雨冰等[12]采用数值模拟的方法，运用Plaxis有限元计算软件模拟宁波市地铁1号线某区间左线隧道在邻近基坑施工时产生较大位移和横向变形。周泽林[13]采用理论分析与数值模拟的方法，在隧道-土体耦合分析基础上，提出了基坑开挖和隧道开挖卸载引起既有隧道变形的计算方法，并借助计算软件进行对比分析。杨凌云[14]采用实测分析的方法，总结归纳近年来9个大型临近隧道基坑开挖项目数据，分析基坑开挖各因素对既有隧道变形的影响，研究既有隧道在临近基坑开挖工况下的施工监测方案与防治措施。这些成果多以数值模拟的方法为基础，辅以实测结果来印证，对基坑开挖过程中周边土体和隧道结构变化过程进行研究。

本次研究以宁波市地铁1号线盾构隧道及周边工程为研究对象，运用Plaxis 2D软件建立有限元模型。计算模型选取基坑宽度B=20 m、基坑开挖深度H=12 m、隧道拱顶埋深h=12 m、隧道与基坑距离l=15 m，主要对隧道拱顶沉降和隧道最大水平位移两项指标进行分析。随后，针对基坑影响隧道变形的4个因素基坑宽度B、基坑开挖深度H、隧道拱顶埋深h、隧道与基坑距离l，设置不同的水平进行单因素敏感性分析和多因素敏感性分析，探讨了基坑开挖卸载对既有运营隧道的影响。

1 土体本构模型

大量土工试验结果表明，土体刚度在受外界扰动过程中会发生变化。随着应变的增加，刚度呈非线性衰减，应变为1%时的刚度已小于最初的一半。土体在基坑开挖过程中的应变属于小应变，应变范围为0.001%～1%。在小应变范围里，土体刚度呈现较高的特性[1-5]。基于以上特点，本文在分析基坑开挖的计算过程中，对土体采用小应变土体硬化模型，即HSS模型。

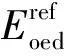
HSS模型的剪切屈服函数在主应力空间的表达式为

(1)

(2)

式中：σ1为最大主应力，σ2为中间主应力，σ3为最小主应力，γp为剪切过程中累积的塑性剪应变，qa为渐近线强度，E50为对应于50%强度的割线强度，Eur为土体的加卸载(回弹)模量。

HSS模型的剪切屈服面与盖帽屈服面在主应力空间中的形状如图1所示。

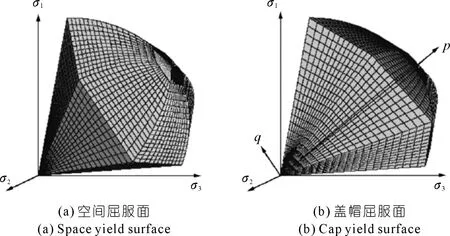
图1 HSS模型空间屈服面和盖帽屈服面Fig 1 Space yield surface and cap yield surface in HSS model

2 数值计算与分析

2.1 数值模型建立

宁波市轨道交通1号线全长46.39 km，于2015年开始运行。由于基坑进行开挖施工作业，在2017年2月至2018年2月间，1号线某临近区间发生局部过大变形。计算模型选取基坑宽度B=20 m、基坑开挖深度H=12 m、隧道拱顶埋深h=12 m、隧道与基坑距离l=15 m，主要对隧道拱顶沉降y和隧道最大水平位移x两项指标进行分析。隧道与基坑位置关系如图2所示。

图2 隧道与基坑位置关系示意Fig.2 Positional relationship between the tunnel and foundation pit

计算分析中，模型的两侧边界采用法向约束，底部边界采用全约束(法向、切向约束)。土体采用三角形15节点单元进行模拟，单元数目为2 654，节点数目为21 899。模型与有限元网格划分如图3所示。其中，隧道衬砌与地下连续墙采用板单元模拟，支撑用点对点锚杆单元模拟，其余均采用实体单元模拟，衬砌、地下连续墙与土体接触面上设置接触单元。衬砌、地下连续墙的计算参数如表1所列。支撑的计算参数如表2所列。

图3 数值计算模型与网格划分Fig.3 Numerical calculation model and meshing

表1 衬砌与地下连续墙计算参数

表2 支撑计算参数Tab.2 Calculation parameters of supporting structure

从地表以下依次分布着7 m厚的① 2淤泥质黏土，4 m厚的② 2-1淤泥，4 m厚的③ 1粉砂，21 m厚的③ 2黏土夹粉砂，12 m厚的④ 1-2粉质黏土和17 m厚的⑤ 2黏土。鉴于HSS模型既可以考虑软黏土的硬化特性，并且其刚度依赖于应力历史和应力路径，计算结果比较合理，因而在本次计算中主要软土本构关系均采用HSS模型。在充分考虑软土力学特性的前提下，同时参考和借鉴其他地区典型软土HSS模型参数，综合确定了本项目软土的HSS模型参数如表3所列。同时根据实际施工顺序，计算分析时按照实际施工过程设置计算步骤，模型计算步骤见表4。

表3 土层HSS模型计算参数[13]Tab.3 Calculation parameters of HSS model[13]

表4 基坑开挖施工步骤Tab.4 Construction steps of foundation pit excavation

2.2 地表竖向位移分析

计算模型各主要施工步骤完成时，竖向位移云图与水平位移云图如图4所示。由图4可以看出，随着基坑开挖深度的增加，基坑内土体卸荷量随之增大。基坑周边土体竖向位移呈现沉降趋势，水平位移呈现靠近基坑的趋势，两者都随着深度的增加而减少。

隧道管片在各开挖深度的沉降位移曲线与水平位移曲线如图5所示。在开挖至坑底时，隧道沉降y=-3.01 mm，隧道最大水平位移x=5.19 mm。

开挖完成后，管片变形如图6所示。基坑开挖过程中，隧道管片受周围土体变形的影响，在竖向发生沉降变形，同时在水平方向上发生向基坑方向变形的趋势。在整个过程中，由于管片刚度的影响，位移管片拱顶沉降比管片底部的要大，截面发生“横鸭蛋”状形变(见图7)。

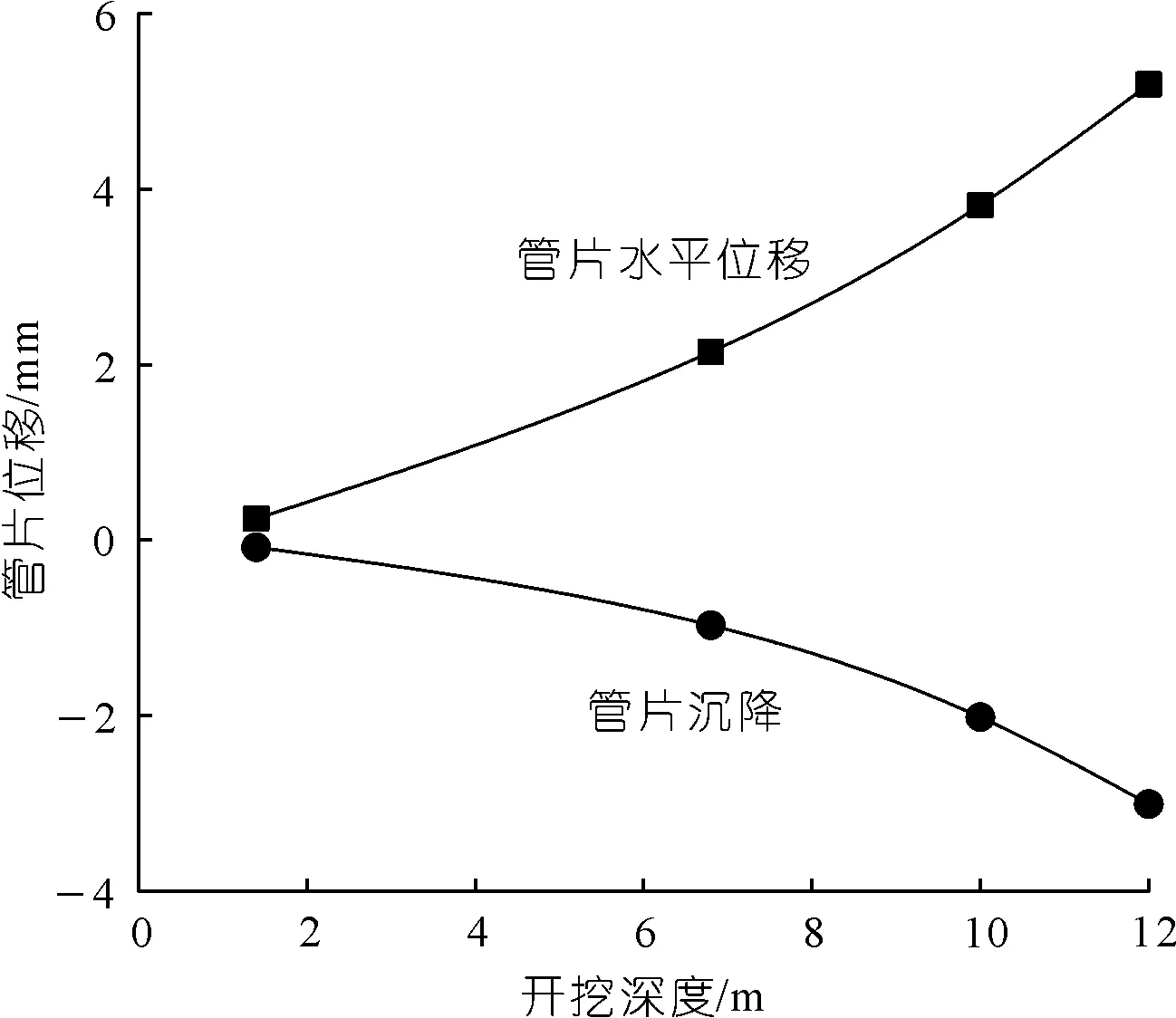
图6 管片位移曲线Fig.6 Segment displacement curve

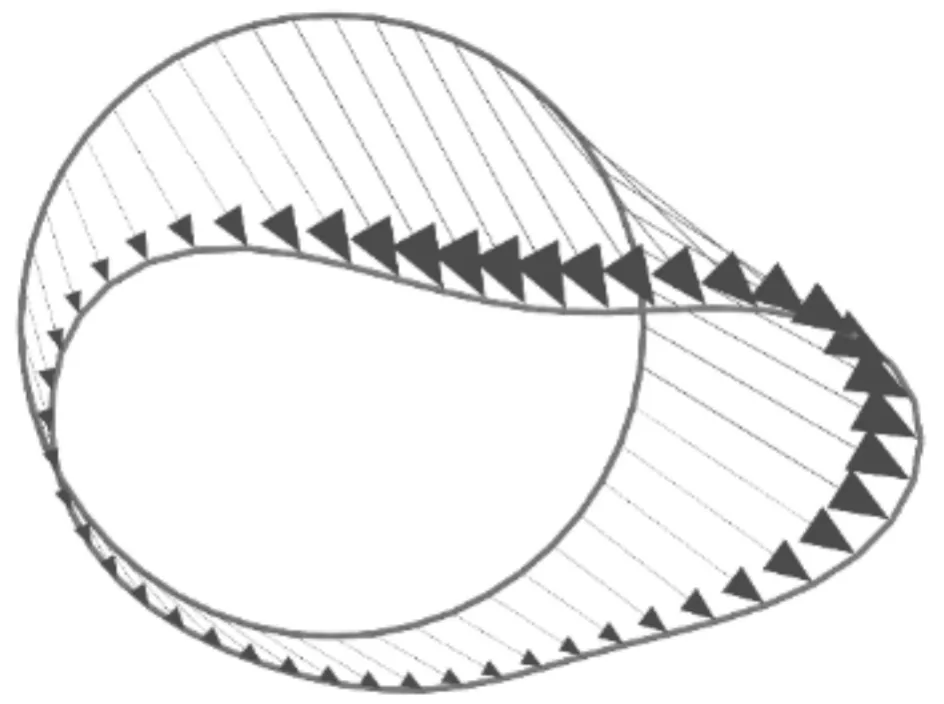
图7 开挖至地下12 m时管片变形(500倍)Fig.7 Deformation of segment when excavating to 12 m underground(500 times)

2.3 参数敏感性分析

2.3.1敏感性分析方法

对于系统特性F可以视为各因素xi的函数，即：

F=f(x1，x2，x3，…，xn)

(3)

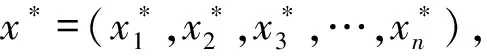
多因素分析考虑了因素之间的相关性，能反映各因素同时变动对结果的影响，主要采用正交设计法[17]。正交试验设计主要过程如下：① 确定试验因素及水平数；② 选用合适的正交表，其中正交表Ln(Sr)表示至多安排r个因素，每个因素有S种水平，共作n次试验的正交表，即n为正交表行数(安排的计算次数)，r为正交表列数(最多可安排因素的数量)；③ 列出试验方案及试验结果；④ 分析正交试验设计结果，对因素的敏感性进行排序，分析正交设计计算数据的方法一般用极差分析法[18]。

2.3.2单因素敏感性分析

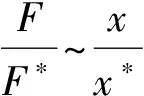
表5 基坑宽度敏感性分析参数Tab.5 Parameters for sensitivity analysis of excavation width

图8 基坑宽度B敏感性关系曲线Fig.8 Sensitivity curve of excavation width B

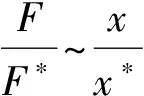
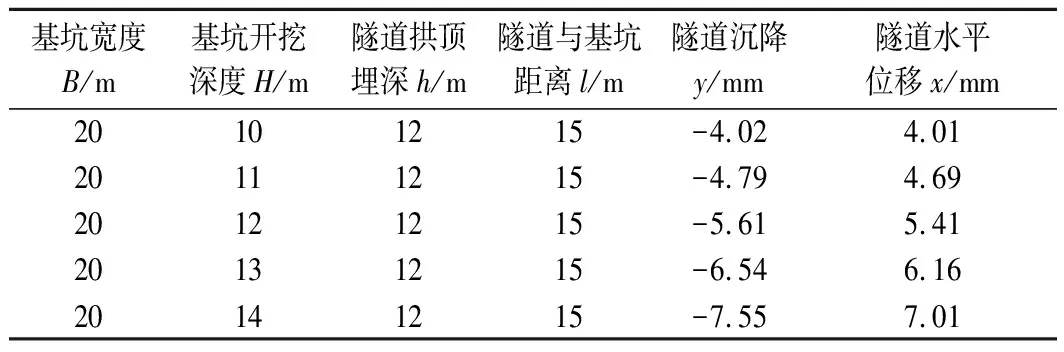
表6 基坑开挖深度敏感性分析参数Tab.6 Parameters for sensitivity analysis of excavation depth

图9 基坑开挖深度H敏感性关系曲线Fig.9 Sensitivity curve of excavation depth H

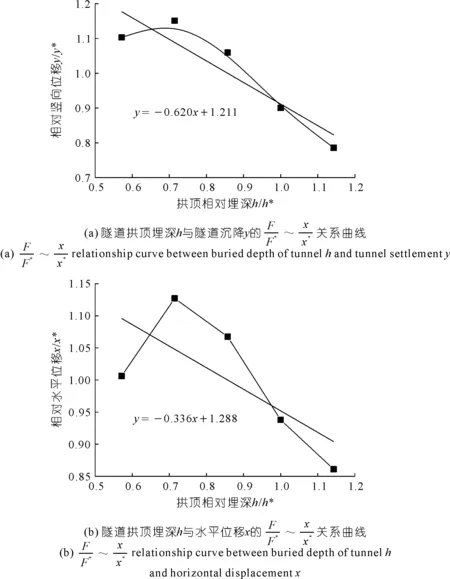
图10 隧道拱顶埋深h敏感性关系曲线Fig.10 Sensitivity curve of buried depth of tunnel h

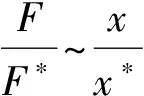
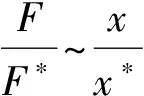
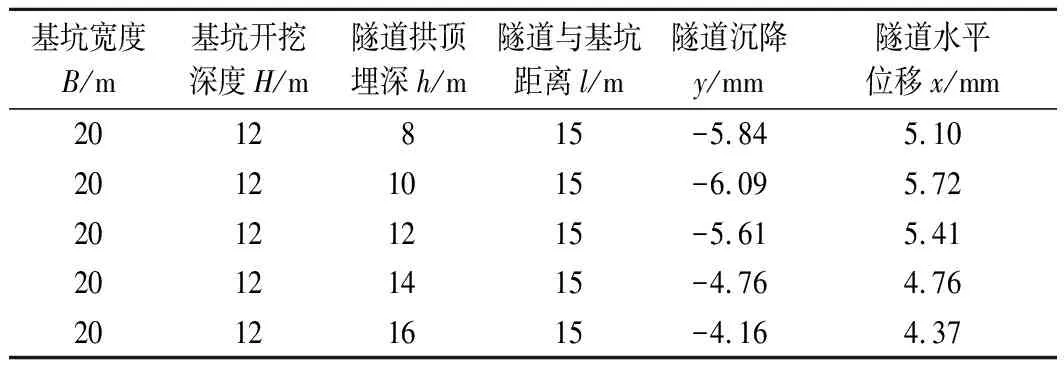
表7 隧道拱顶埋深敏感性分析参数Tab.7 Parameters for sensitivity analysis of buried depth of tunnel vault

表8 隧道与基坑距离敏感性分析参数Tab.8 Parameters for sensitivity analysis of distance between tunnel and foundation

图11 隧道基坑距离l敏感性关系曲线Fig.11 Sensitivity curve of distance l between tunnel and foundation

从图8，9，11可以看出，考虑基坑宽度、基坑开挖深度和基坑与隧道距离影响的隧道变形敏感性关系曲线均呈线性变化，其中，隧道变形与基坑宽度和开挖深度呈正相关，而与基坑隧道间距呈负相关。即，随着基坑宽度和基坑开挖深度的增加，隧道变形与所受影响程度随之增加；而随着基坑与隧道距离的增加，隧道变形与所受影响程度逐渐减小。隧道竖向位移和水平位移在隧道拱顶埋深为12 m时为最大值，之后随隧道拱顶埋深额增大，逐渐减小，表明隧道埋深12 m是一个隧道埋深对隧道变形影响的临界点。

在影响隧道沉降的因素中，基坑开挖深度H、隧道与基坑距离l、基坑宽度B3个因素中最大与最小的敏感性相差38.5%，而隧道拱顶埋深h与上述三者敏感性平均值相差53.8%。在影响隧道水平位移的因素中，基坑开挖深度H、隧道与基坑距离l、基坑宽度B3个因素中最大与最小的敏感性相差42.0%，而隧道拱顶埋深h与上述三者敏感性平均值相差74.4%。基坑开挖深度H、隧道与基坑距离l、基坑宽度B均为影响隧道沉降和水平位移的重要因素，而隧道拱顶埋深h产生的影响相对较小。

单因素分析法分析结果表明：不同参数对隧道管片的竖向位移和水平位移的影响程度不尽相同，但总体而言，影响隧道沉降和水平位移的参数敏感性由大到小依次均为基坑开挖深度H、隧道与基坑距离l、基坑宽度B、隧道拱顶埋深h。

2.3.3多因素敏感性分析

选择正交表L9(34)对隧道与基坑的参数进行敏感性分析，并进一步采用极差分析法分析正交计算结果。因素水平选取如表9所列。根据正交设计计算方案，用有限元方法计算相应的隧道沉降y与隧道水平位移x，正交设计计算方案及结果见表10。从表10可以看出，工况4对应的隧道拱顶沉降和隧道水平位移最小，是隧道变形控制的最佳方案。

表9 因素水平Tab.9 Factor levels m

根据极差分析法分析正交实验设计结果，隧道水平位移x与隧道沉降y分析结果如表11及表12所列。可以看出，基坑宽度和基坑开挖深度两个因素引起的隧道变形平均沉降量逐渐递增，而隧道与基坑距离造成的影响则与之相反。同时，不同因素影响下隧道竖向位移和水平位移的极差不同，具体为当研究不同参数对隧道竖向位移影响时，基坑开挖深度对应的极差最大，而隧道拱顶埋深对应的极差最小，表明基坑开挖深度对隧道沉降的影响最为显著，隧道拱顶埋深的影响最不明显。同理，分析不同参数对隧道水平位移影响时，隧道与基坑距离对应的极差最大，而隧道拱顶埋深对应的极差最小，表明隧道与基坑距离对隧道沉降的影响最为显著，隧道拱顶埋深的影响最不明显。由分析结果得出，隧道沉降的参数敏感性由大到小依次为：基坑开挖深度H、隧道与基坑距离l、基坑宽度B、隧道拱顶埋深h，其影响次序与单参数分析结果一致。隧道水平位移的参数敏感性由大到小依次为：隧道与基坑距离l、基坑开挖深度H、基坑宽度B、隧道拱顶埋深h。

表10 正交设计计算方案及结果Tab.10 Calculation schemes and results of orthogonal design

表11 隧道沉降的各参数极差分析Tab.11 Range analysis of parameters of tunnel settlement mm

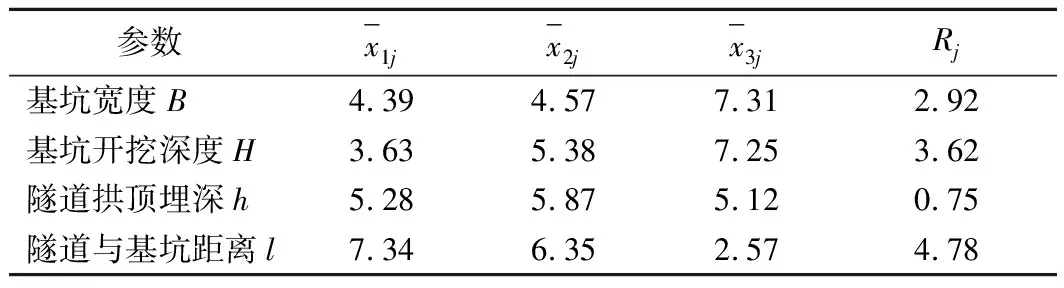
表12 隧道水平位移的各参数极差分析Tab.12 Range analysis of parameters of tunnel horizontal displacement mm

研究成果表明：考虑了多因素影响时，对于隧道沉降而言，基坑开挖深度H、隧道与基坑距离l、基坑宽度B3个因素中最大与最小的敏感性相差31.9%，而隧道拱顶埋深h与上述三者敏感性平均值相差69.0%。对于隧道水平位移而言，隧道与基坑距离l、基坑开挖深度H、基坑宽度B3个因素中最大与最小的敏感性相差38.9%，而隧道拱顶埋深h与上述三者敏感性平均值相差80.1%。基坑开挖深度H、隧道与基坑距离l、基坑宽度B均为影响隧道沉降和水平位移的重要因素，而隧道拱顶埋深h产生的影响较小。

3 结 论

(1) 不同工况下的数值模拟结果表明，基坑开挖影响下，临近既有隧道管片位移随基坑开挖深度的增大而逐渐增大。隧道管片竖向位移表现为沉降，水平位移表现为向基坑方向移动。管片呈现“横鸭蛋”状变形模式。

(2) 单因素分析结果表明，不同参数对隧道管片的竖向位移和水平位移的影响程度不尽相同。其中，基坑开挖深度H、隧道与基坑距离l、基坑宽度B3个因素中最大与最小的敏感性相差38.5%，而隧道拱顶埋深h与上述三者敏感性平均值相差53.8%；在影响隧道水平位移的因素中，基坑开挖深度H、隧道与基坑距离l、基坑宽度B3个因素中最大与最小的敏感性相差42.0%，而隧道拱顶埋深h与上述三者敏感性平均值相差74.4%。影响隧道沉降和水平位移的参数敏感性由大到小依次均为基坑开挖深度H、隧道与基坑距离l、基坑宽度B、隧道拱顶埋深h。

(3) 多因素分析结果表明，对隧道沉降而言，基坑开挖深度H、隧道与基坑距离l、基坑宽度B3个因素中最大与最小的敏感性相差31.9%，而隧道拱顶埋深h与上述三者敏感性平均值相差69.0%，表明隧道沉降的参数敏感性由大到小依次为基坑开挖深度H、隧道与基坑距离l、基坑宽度B、隧道拱顶埋深h，其影响次序与单参数分析结果一致。对隧道水平位移而言，隧道与基坑距离l、基坑开挖深度H、基坑宽度B3个因素中最大与最小的敏感性相差38.9%，而隧道拱顶埋深h与上述三者敏感性平均值相差80.1%，表明隧道水平位移的参数敏感性由大到小依次为隧道与基坑距离l、基坑开挖深度H、基坑宽度B、隧道拱顶埋深h。

(4) 单因素与多因素分析结果表明，基坑开挖深度、隧道与基坑距离、基坑宽度均为影响隧道沉降和水平位移的重要因素，而隧道拱顶埋深产生的影响较小。

本文所依托工程项目由于支护体系完善且基坑开挖方式合理，隧道变形均在规范要求范围内，满足设计要求。本文主要目的是依托该工程，研究基坑宽度、基坑开挖深度、隧道拱顶埋深以及隧道与基坑距离等因素对隧道变形的影响，进一步为类似工程的设计提供一定指导，以确定合理的基坑开挖间距、基坑设计宽度和基坑开挖深度。