基于支持向量机和贝叶斯方法的岩体参数反分析

张 雅 贤，侯 中 杰

(1.中央军委后勤保障部安置住房保障中心，北京 100036； 2.重庆大学 土木工程学院，重庆 400045)

0 引 言

随着对岩土体认识的不断深入，人们就岩土体本身的性质具有不确定性这点达成了共识。在岩土体参数不确定性表征方面，国内外学者做了大量研究工作。主要的表征方式为基于统计特征的概率分布形式，包括正态分布[1-2]、对数正态分布[3-4]、Beta分布[5]、极值I型和Weibull分布[6]。早期学者们主要是采用随机变量模型来对岩土参数的不确定性加以研究。然而，类似的研究在刻画岩土材料的随机特性时都是将同层岩土体看作均质材料，即仅在抽样时对参数取不同数值，而针对同一样本在不同空间处的参数却往往取的是同一值，这样可能导致与实际情况不相符合。近些年来随着土体空间变异性概念的提出[7]，众多学者开始采用参数随机场模型来研究岩体参数并取得众多研究成果，这意味着对岩体参数的研究实现了从“点特性”到“空间特性”的转变。Degroot等[8]为了更好地研究土体参数的自相关性，引入了极大似然估计法以及相关函数法。Phoon等[9-10]则采用统计学理论分析了不同实验参数转换的相关性、不确定性以及不同岩土材料的变异性等问题。梅松华等[11]结合工程实例，采用不同的方法实现了对土体参数相关距离的求解。随着随机场模型的进一步应用，众多以空间随机场作为理论基础的岩土工程可靠性分析方法逐渐被广泛应用[12-16]。

当前，学术界在岩土工程参数不确定性方面开展的研究非常多。但是截至目前，学术界和工业界仍尚未形成基于整个施工过程的岩土参数不确定性分析方法，而与岩土参数不确定性表征方式相关的研究则较为常见。为此，本文在岩体参数识别的基础上，融合贝叶斯理论与多输出支持向量机算法，提出基于位移与松弛深度的岩体参数概率反分析方法，并以白鹤滩水电站左岸坝基边坡为例，研究了边坡岩体参数的不确定性特征及其随施工开挖的动态更新过程。

1 多输出支持向量机和贝叶斯方法原理

1.1 多输出支持向量机原理

多输出最小二乘支持向量机(MSVM)主要源自早期的单输出支持向量机(SVM)[17-20]。对样本集为{(x1，y1)，(x2，y2)，…，(xl，yl)}，x∈Rd，y∈Rm，其中，l、d和m分别表示样本数、输入变量的维数和输出变量的维数，多输出最小二乘支持向量机(MSVM)对应的最小化问题为

(1)

式中：wi为权向量，b为阈值向量，e为误差，φ1(xi)为核函数，γ为误差因子。引入Lagrange乘子α，将式(1)转化为

(2)

以w、b、e和α为自变量对式(2)求偏导，并令偏导等于零，易得：

(3)

i=1，2，3，…，l；j=1，2，3，…，m

从而能形成关于w、b、e和α的线性方程，对该方程求解即可得出多输出最小二乘支持向量回归函数表达式：

(4)

式中：K(xi，x)=φ(xi)·φ(x)。

1.2 贝叶斯方法原理

贝叶斯方法(Bayesian method)基于概率理论，在已知事情结果的情况下反推事情发生的原因。假设随机事件A发生的概率为P(A)，随机事件B发生的概率为P(B)，那么A在B发生的情况下发生的概率P(A|B)为

(5)

这就是贝叶斯公式的最核心的一般表达式，将上式运用到反分析中时，事件A则是先验信息，B是观测结果，运用观测结果来反推先验信息就是反分析。式(1)所示的贝叶斯公式是参数反分析的基础。

(6)

式中：p(b|a)称作似然函数。此时，根据式(5)所示的贝叶斯理论得到样本与参数的联合分布为

d(b，a)=p(b|a)Rp(a)

(7)

在有观测信息b的情况下，再对参数a进行新的估计。考虑到：

d(b，a)=R(a|b)z(b)

(8)

式中：z(b)是b独立的边缘概率密度函数，求解方法为

(9)

由式(8)得到参数a的估计：

(10)

根据统计资料，有先验分布Rp(a)，观测资料为b，则代入式(6)就能推断出参数a新的概率分布。这种新的分布融入了实测资料，将更加准确，称之为后验分布。

由以上可知，为推断出可靠的后验参数估计，先验信息尤为关键。有限的先验信息一般通过实地钻孔测量得到，或者通过大量的文献调查类比得到。得到先验信息后，可根据不同的参数选择不同构建先验分布的方式，常用高斯曲线来构建概率密度函数，利用均值和变异系数来构造高斯函数作为先验分布。

2 位移-松动圈与岩体参数间的支持向量机模型

2.1 模型建立

参数的不确定性是直接影响工程设计及安全性评价可靠性的重要因素。采用多输出支持向量机(MSVM)建立监测位移与岩体参数之间的关系，然后采用贝叶斯方法融合已有的信息对岩土力学参数不确定性分布规律做出合理的估计。MSVM可用于表征监测位移、松动圈与弹性模量等岩土力学参数之间存在的非线性关系，MSVM(X)模型定义如下：

(11)

式中：X=(x1，x2，…，xN)，xi是岩土力学参数(如弹性模量、摩擦角等)组成的向量，N为力学参数的个数。Y=(y1，y2，…，yQ)是监测数据的Q维向量，包括位移和松弛深度。

将贝叶斯理论融合在MSVM模型中，不同测点力学参数与位移松弛深度之间的关系可以通过MSVM模型得出。监测点的预测结果(y1，y2，…，yk)与相应的监测结果(可以用Ymon1，Ymon2，…，Ymonk来表示)相等的可能性是参数θ的条件概率密度函数，即：

(12)

模型参数的先验分布f(θ)由参数的均值向量μθ=(μθ1，μθ2，…，μθn)和协方差矩阵Cθ给定[21]，其中：

(13)

(14)

式(12) 中的Nk(y)定义如下：

(15)

(16)

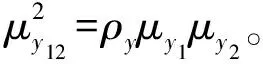
后验分布可以通过优化方法获取，在求得后验均值之后，可用下式求得后验标准差：

(17)

其中，

(18)

(19)

2.2 模型实现基本步骤

B-MSVM采用贝叶斯算法更新岩土力学参数，并且考虑了岩土体内在的不确定性。位移-松弛深度与岩土力学参数的对应关系对更新算法至关重要，本文采用 MSVM来取代传统的数值分析或模型计算方法，其主要步骤如图1所示。

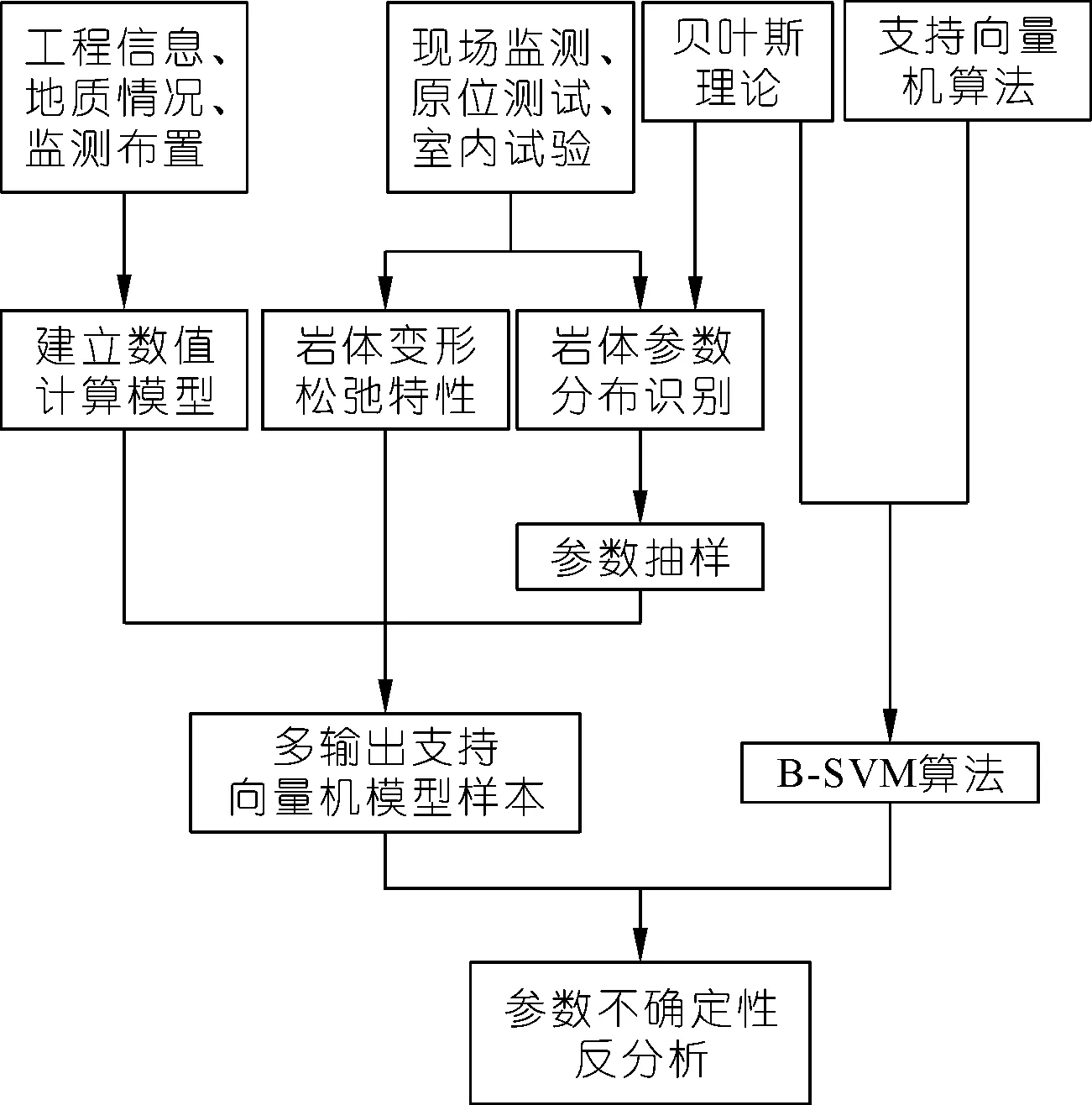
图1 基于支持向量机和贝叶斯方法的反 分析基本步骤Fig.1 Basic steps of back analysis based on support vector machine and Bayesian method

(1) 收集监测面分布、地质条件等实际工程信息，并借助ABAQUS、Phase2等主流有限元软件建立数值模型。

(2) 根据步骤(1)中所收集到的工程信息，对用于识别的训练组参数分布类型及其范围加以确定，并通过抽样法构建目标样本。

(3) 借助数值模型计算确定样本位移。

(4) 构建MSVM样本。构建岩土力学参数组合，样本集由采样点及其数据构成。通过有限元法或其他方法确定每个样本集的松弛深度、位移并定义MSVM模型。通过对公式(2)求解进而获得MSVM 模型。

(5) 由公式(12)建立贝叶斯更新模型，并计算识别参数。

(6) 由公式(17)确定参数的后验标准差，并进一步得到岩土力学参数。

(7) 根据新的开挖步中监测数据，实时更新土体参数和不确定性分布情况。

3 工程实例应用

3.1 工程简介

白鹤滩水电站左岸坝基边坡如图2所示。边坡主要由砂岩、泥岩、灰岩、凝灰岩组成。裸露的岩石主要有6类：泥岩石灰岩互层、泥岩石灰岩混合岩、层状凝灰岩、砂岩、砂岩泥岩互层、泥岩。左坝肩属陡峭的反倾岩质边坡，开挖高度从635 m降低到215 m，高差达420 m，开挖切角的范围35°～65°，分布约14个15～20 m高的长椅状台阶。边坡上存在50多个大大小小的断层，较大的断层对边坡的稳定性有很大影响。

图2 白鹤滩水电站左岸坝基边坡实景图Fig.2 Realistic view of left bank dam foundation slope of Baihetan Hydropower Station

为记录开挖期间及开挖完成之后边坡的变形，共选取了13条监测剖面，位置分布如图3所示。监测表面位移和深部变形的仪器均在边坡上沿着监测剖面布置，这些仪器可以监测边坡的变形情况，现场收集了通过多点伸长计记录的变形数据。

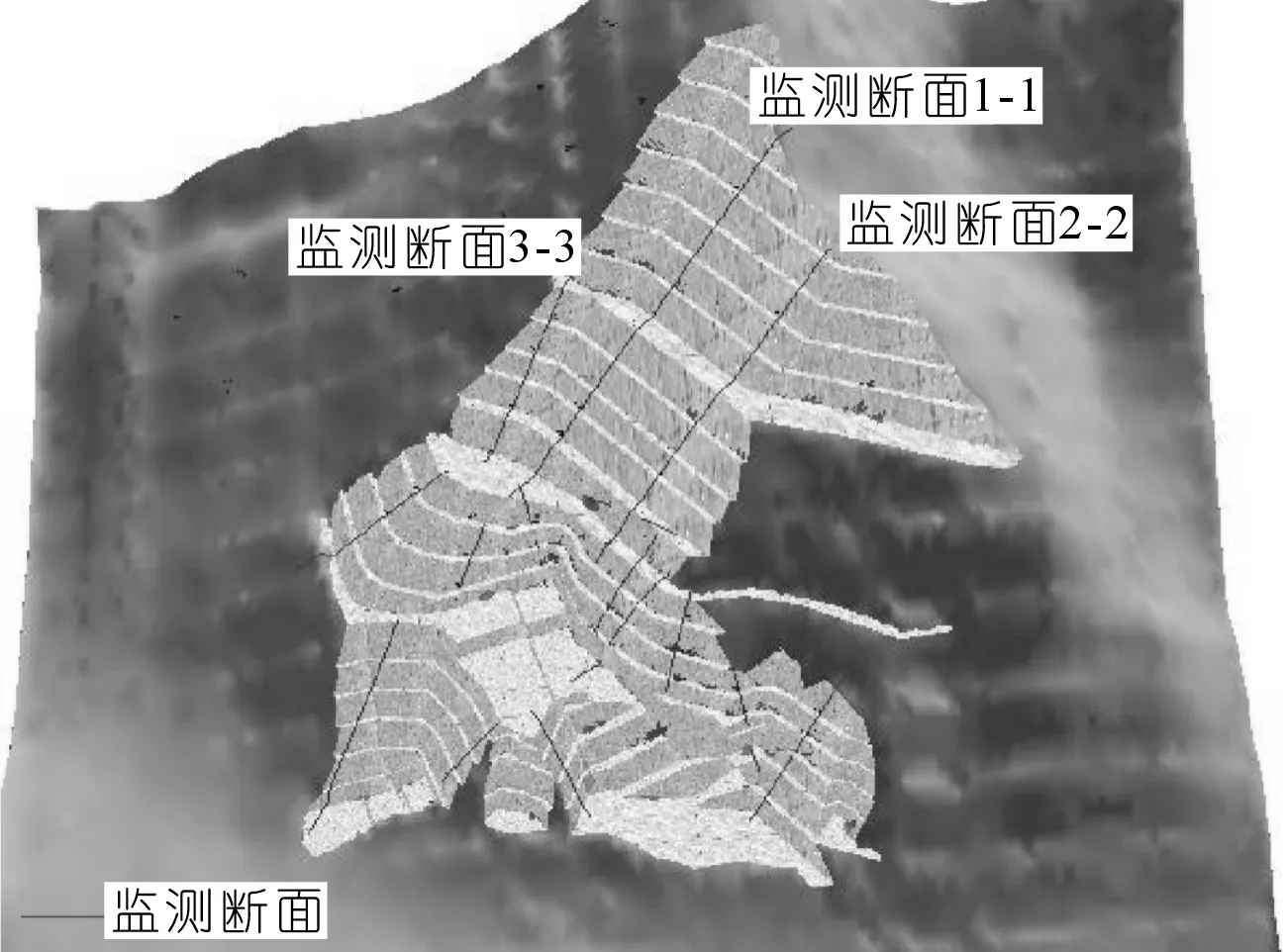
图3 监测断面位置示意Fig.3 Location of monitoring section

柱状节理玄武岩在边坡测试区域内集中发育，且柱状节理被较多的缓倾角结构面和错动带切割，除一些受构造影响的区域，柱状节理玄武岩的柱体轴线倾角基本均为60°～80°。

3.2 反分析过程

选取典型的监测断面1-1来反演边坡岩土体的力学参数，沿着1-1地质剖面的岩床包括砂岩、砂岩泥岩互层、泥岩等。此外，考虑了12个重要的断层建立有限元数值模型。数值计算中破坏准则采用摩尔库伦准则，断层采用节理单元模拟。据原位应力测试的结果，采用式(20)、(21)模拟计算原位应力。对于全风化和强风化的岩体：

(20)

式中：σx和σy分别表示与深度方向垂直的x方向和y方向的原位应力，σz表示深度方向上的应力，γ表示岩石密度，μ表示泊松比，h表示岩石上覆层的厚度。

对弱风化和无扰动的岩体：

(21)

式中：Kx和Ky分别表示原位应力在x水平方向和y水平方向的侧压力系数。

通过数值模型、现场试验或者室内试验可以计算得出复合岩体的物理力学参数。根据给定的边坡稳定性要求，反分析计算出符合正态分布的9个岩土力学参数：主要包含7个弹性模量，其中1个是弱风化岩体的弹性模量，另6个是6种岩体的弹性模量；另外2个参数是弱风化岩体和无扰动岩体的原位应力测试的侧压力系数。考虑这9个参数的原因一方面是因为这些参数对边坡稳定性有较大影响；另一方面是因为如果选择更多的参数会导致计算过程更为复杂，工程应用较为不便。

利用拉丁超立方体抽样方法建立了一个总数为50的样本组。基于前文的数值模型，采用有限元软件计算每个样本参数对应的位移值，生成50组含有不同岩土力学参数和位移的训练样本。借助MSVM算法来进一步刻画岩土力学参数与位移之间的联系。采用同样方法构建20个MSVM模型测试样本。通过研究计算位移与MSVM预测位移之间的联系得出两者的对比如图4所示。分析图4可以得知两者具有较高一致性，该对比结果也说明在概率反演分析中可用MSVM方法替代数值模型。

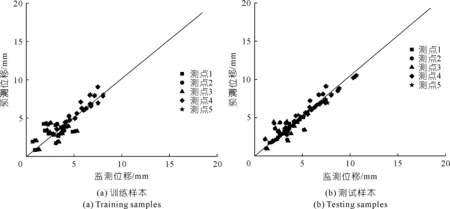
图4 有限元计算位移和MSVM预测位移的对比Fig.4 Comparison of displacement calculated by FEM and predicted by MSVM

3.3 结果比较及验证

基于本文提出的反分析方法，可以得到14个不同开挖步条件下7种不同岩体的弹性模量和2个原位侧压力系数。为了探讨不同开挖条件下B-MSVM方法的适用性，又进行了两阶段分析；第一阶段是采用监测点的位移反分析计算了13个开挖步后的岩土力学参数；第二阶段是基于第一阶段获取的岩体参数的平均值和标准差，采用第14个开挖步后的位移反分析计算岩土力学参数。

不同开挖步下由计算结果反演的岩土力学参数分布如图5所示。 随着开挖的进行，每个开挖步下参数的分布变窄，标准差也随之降低。这种参数分布的变化表明，所提出的方法可以更加准确地进行反分析，同时所提出的模型可以用于指导工程设计和施工。

通过监测点的附加信息和数据生成的标准差加深了对岩土力学参数不确定性的理解。与传统的反分析方法相比，概率反分析提供了更多的关于岩土力学参数的信息，并用一种切实可行的方式体现了岩土力学参数的不确定性。这种方法比确定性方法更合理，并能更进一步地匹配地质工程的复杂性和不确定性特征。

采用有限元数值软件基于已识别的参数计算了监测点的位移，结果如图6所示。基于参数识别计算的位移和实测位移具有较好的一致性。基于参数识别的第二阶段计算位移比第一阶段计算位移更接近实测位移，这表明位移的持续更新能提高反分析模型的准确性，概率反分析可以用来进行边坡的可靠度分析和可靠度设计。

MSVM方法预测的监测点的位移分布如图7所示。图中位移分布变窄，岩土体参数分布也变窄，这表明附加的开挖信息降低了预测位移的不确定性。这不仅说明了位移的不确定性，也说明更多的监测信息(先验信息)可以有效地降低不确定性的影响。

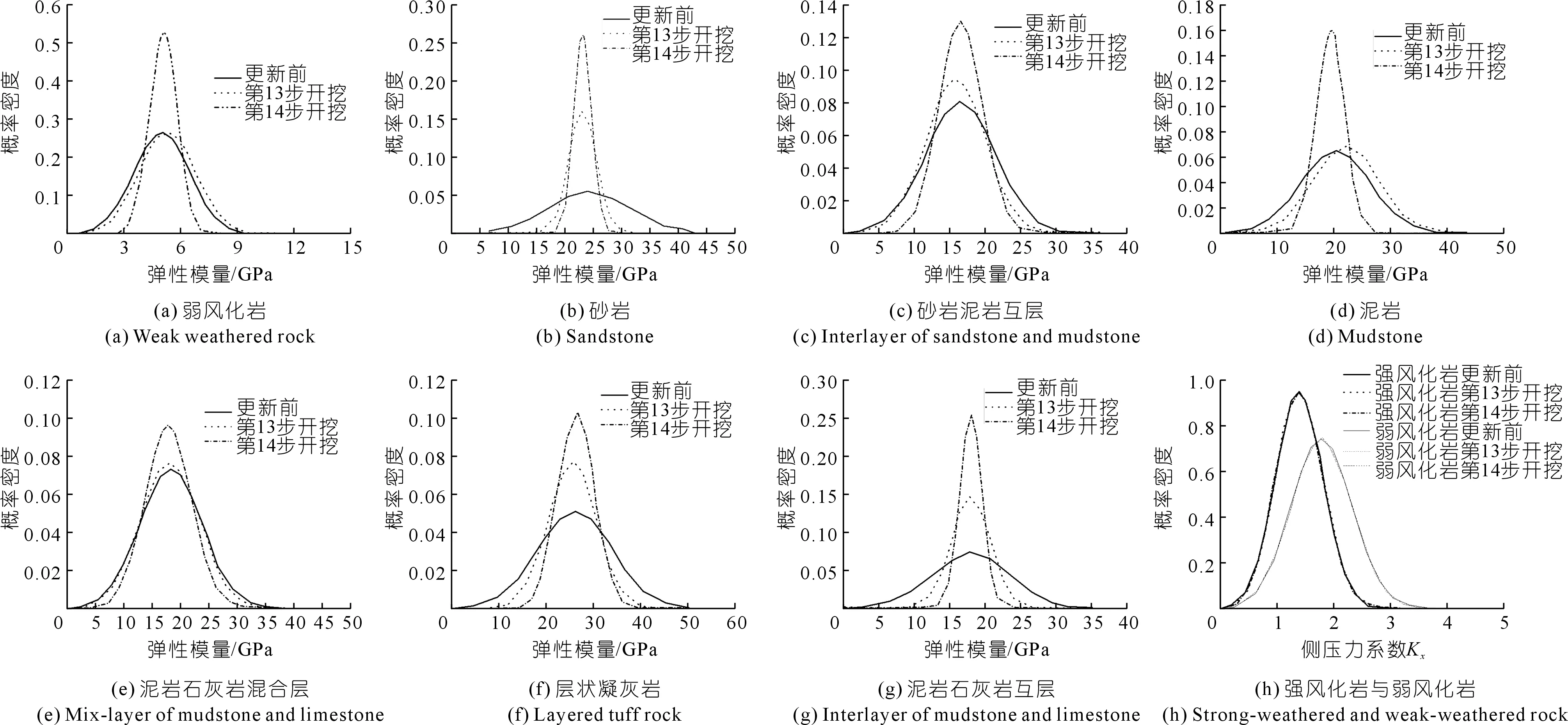
图5 不同开挖步下不同参数的不确定性对比Fig.5 Comparison of uncertainty of different parameters under different excavation steps

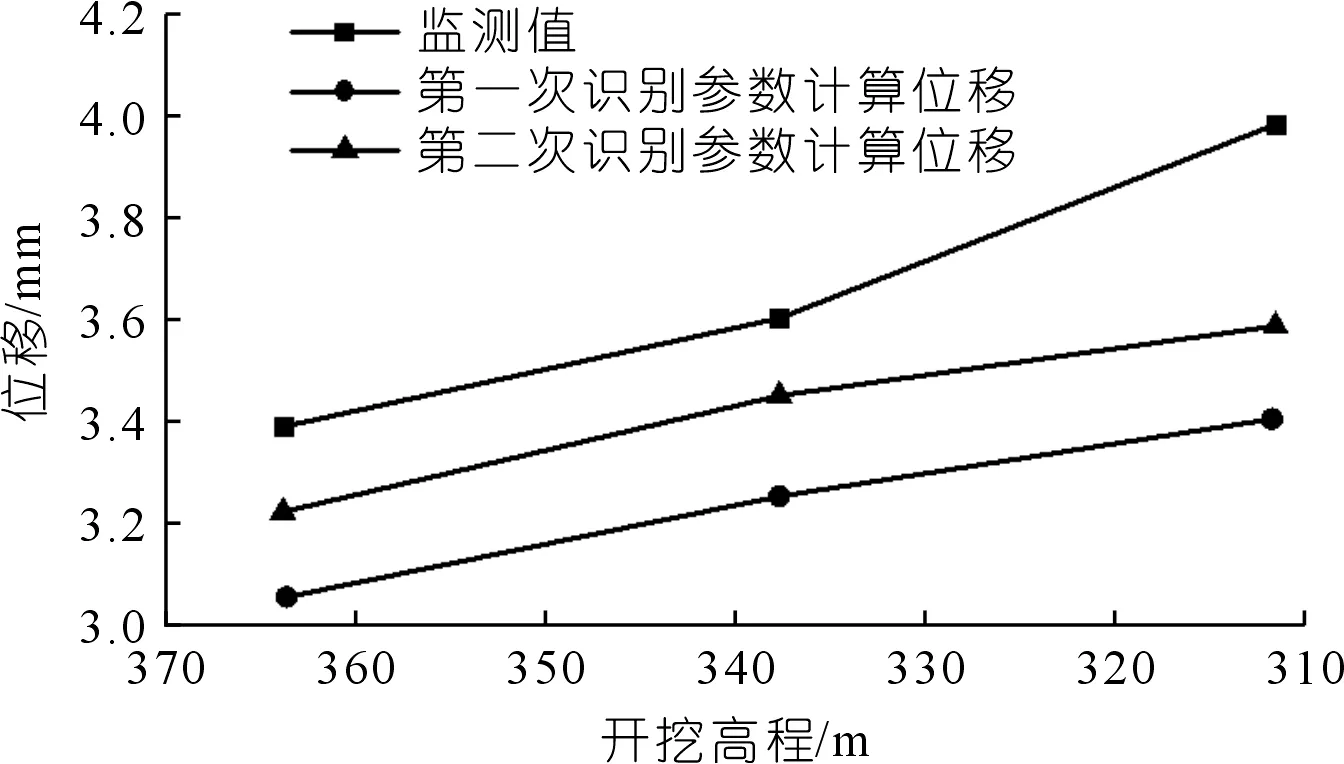
图6 监测点的计算位移与预测位移对比Fig.6 Comparison of calculated displacement and predicted displacement of monitoring points

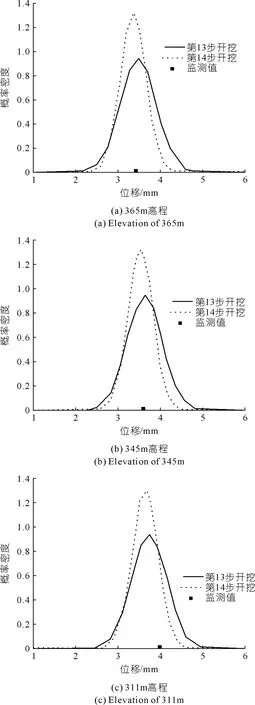
图7 不同高程开挖时B-MSVM法预测的监测点位移 分布对比Fig.7 Comparison of displacement distribution of monitoring points predicted by Bayesian-MSVM method during excavation at different elevations

4 结 论

将多输出支持向量机方法和贝叶斯理论引入到了边坡岩体物理力学参数的不确定性反分析过程之中，从而实现参数的不确定性表征，并且实现了不确定性特征随着施工过程的动态更新。提出基于位移与松弛深度的岩体参数概率反分析方法，将该方法应用于白鹤滩水电站左岸坝基边坡，主要得出如下结论：

(1) 概率反分析方法提供了更多的关于岩土力学参数的信息，比确定性方法更合理，并能更进一步地匹配地质工程的复杂性和不确定性特征。

(2) 更多的监测信息(先验信息)可以有效降低不确定性的影响，位移的持续更新能提高概率反分析模型的准确性，相应的反分析的结果可以用来进行边坡的可靠度分析和可靠度设计。

(3) 本文提出的方法可以实现参数及其不确定性特征随施工过程的动态更新，可以推广应用到类似工程中。