基于大数据的纯电动客车动力电池健康状态估算方法研究

南金瑞， 张 林， 曹万科， 何 泳， 叶许成， 张 峰

(北京理工大学 深圳汽车研究院，深圳518000)

为确保纯电动汽车的安全和正常使用，有必要对动力电池的性能进行实时测量和预警，作为一项评价电池安全和性能的关键参数——健康状态(SOH)，越来越受到政府部门和相关单位的重视[1].

近年来，随着车载电器设备的逐年增多，CAN总线通讯技术因可实现数据共享、降低制造成本等优势在车辆上得到广泛应用.汽车CAN总线系统简单来说就是在汽车内部搭建的一个局域网,以实现每个电控单元之间的信息共享[2].因此，通过CAN总线采集电池数据也是现今的主流方式.

目前部分新能源汽车BMS(电池管理系统)已具有实时预估SOH功能，但其大多基于实验室单体电池仿真模拟的SOH曲线，通过监测动力电池的实时部分指标如内阻等而计算得出SOH[3].这种方式一般在新能源汽车刚投入使用时估测比较准确，随着充放电次数的增加，误差也越来越大.而企业监测平台和车载终端的采集数据则以实际工况为基础，数据是动力电池实际运行中所受到的多种因素影响的集中体现[4].因此，以纯电动客车CAN总线通讯的广泛应用为前提，采用纯电动客车实时运行的大数据来进行动力电池SOH的研究，可以提高SOH预测的准确和及时性，确保纯电动客车动力电池的使用安全[5].

1 动力电池SOH的影响因素和估算模型的建立

1.1 动力电池SOH的影响因素

在实际使用中，由于受到多种因素的影响，研究分析电池健康状态SOH和老化原因却十分复杂[6].

对电池健康状态的分析，如果仅仅涉及某一因素或某一些因素，将导致结果严重偏离实际，而基于全部相关因素，虽然准确性高，但过程繁杂，最终可能难以实现.采用合适的数学方法，对锂离子电池实时充放电大数据进行处理和分析，实现动力电池SOH的估算更加实际和方便[7-8].

1.2 实时采集的纯电动客车运行数据分析

文中主要研究纯电动客车的营运过程的规律，在车辆使用运行过程中，大数据平台会采集到海量的车辆数据，但是在运行过程中，电池放电受负载、车速、路况、驾驶员等多种因素的影响，统计的数据没有规律性，变化较大，用于分析研究SOH比较困难；相较而言，在充电过程中，车辆始终处于静止状态，受外界因素干扰小，充电电流基本稳定，总电压和SOC平稳上升，显然，充电过程的数据比较规律、简单、易于统计.

1.3 动力电池SOH模型的建立

文中采用充电数据进行SOH预测估算，假设动力电池从0初始容量开始充电，则

(1)

式中：C0为动力电池出厂时的标称容量；t1为动力电池从初始时刻0时刻充电到截至电压所需的时间；I为动力电池的恒流充电电流.

该方法计算简便，C0标称容量很容易可以获得；仅仅是动力电池每次从容量初始值0恒流充电截止电压的时间无法直接获得.目前在大数据平台有车辆下线后的全部数据，而车辆运营初始阶段一般可将动力电池SOH视为100%，故可以计算出初始阶段动力电池全充时间.显然，只要从后续的每次充电片段数据估算出当次的全充时间，即可实现对所有充电时刻SOH的估算.

2 融合高斯过程回归的扩展卡尔曼滤波SOH算法构建

2.1 扩展的卡尔曼滤波理论

在实际中，纯电动客车动力电池的工作特性，往往呈现出杂乱无章的非线性特点，为了更好地描述动力电池的行为特点，进一步提高SOH预估的准确性，文中采用扩展卡尔曼滤波.

扩展卡尔曼滤波的核心思想是：在卡尔曼滤波基础上，通过对非线性函数线性化，实现卡尔曼滤波对非线性系统的应用扩展[9].扩展的卡尔曼滤波过程和卡尔曼滤波一样分为两个过程：预测过程和更新过程，具体公式如下.

,

(2)

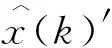
p(w)～N(0,Q).

(3)

2.2 融合高斯过程的扩展卡尔曼滤波

高斯过程回归是使用高斯过程对数据进行回归分析的非参数模型.高斯过程主要具有以下两个优点[10]：①无论随机变量如何组合，只要组合方式是线性的，都服从高斯分布；②期望和协方差函数确定了高斯过程的全部性质.

如果充分利用数学模型和数据模型的各自优势，将高斯过程回归和扩展卡尔曼滤波两种算法相融合，则可以构建出一个高精度滤波模型.在这个模型中，通过高斯过程回归的训练数据学习，可以获得扩展卡尔曼滤波的状态方程和测量方程以及协方差，进一步计算得出扩展卡尔曼滤波中所需的每一个状态估计值，从而保证了扩展卡尔曼滤波递推的正常进行[11-12].

模型的过程如下：对于循环cyclei，已取得上一循环i-1的训练数据：Dcyclei-1=[zcyclei-1(1)，zcyclei-1(2)，…，zcyclei-1(k)]；zcyclei(k)为循环i下的第k个观测量；高斯过程回归的输入值xcyclei(k)为循环i下的第k个状态量.对循环i进行扩展卡尔曼滤波，其对应的状态方程和测量方程如下.

xcyclei(k)=GPf[xcyclei(k-1),ucyclei(k-1)]+w(k),

(4)

zcyclei(k)=GPh[Dcyclei-1,x(k)]v(k),

(5)

(6)

(7)

式中：R，Q为信号方差；GP表示高斯过程回归.

考虑到曲线的特点，文中选用线性函数作为高斯过程回归的均值函数，同时，选择自动相关性确定(ARD)理性平方协函数作为核函数，即

m(x)=ax+b,

(8)

,

(9)

式中:k(xp,xq)为高斯过程回归的自动相关性确定(ARD)理性平方协函数;σf为信号标准差；σm为单独长度尺度；α为正向尺度混合系数.

此时高斯过程回归的超参数θ={a,b,σf,σm,α}.

2.3 融合高斯过程回归的扩展卡尔曼滤波SOH算法模型

文中主要研究基于纯电动客车大数据平台采集到的动力电池充电数据来估算纯电动客车动力电池SOH的方法.融合高斯过程回归的扩展卡尔曼滤波SOH算法模型如图1所示.

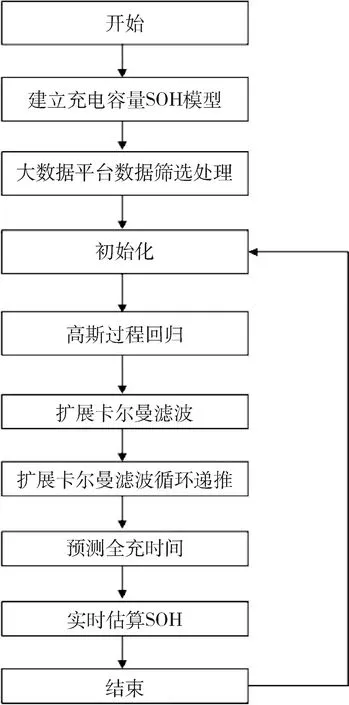
图1 融合高斯过程回归的扩展卡尔曼滤波SOH算法模型图

(1)大数据平台数据筛选处理

对大数据平台采集的相关数据进行筛选处理，使之满足本算法的要求.

(2)初始化

已知如下数据：动力电池组恒流充电电流I；动力电池组恒压充电截至电压U截至；循环cyclei对应的充电数据Dcyclei=[(tcyclei(k),Ucyclei(k))|k=1,…,ni]，tcyclei(k)是具体的数据采样时间,而且其间隔ΔT=tcyclei(k)-tcyclei(k-1)为固定值；Ucyclei(k)为动力电池组的实时电压值.

数据初始化，即i=0，初次循环为cycle0：I、V截至、tcycle0(k)、Ucycle0(k)、ΔT、初次循环恒流充电的全充数据Dcycle0=[(tcycle0(k),Ucycle0(k))|k=1,…,n0]，n0为初次循环动力电池组达到V截至时的总采样时间点个数.

(3)高斯过程回归

文中选用线性函数m(x)=ax+b作为高斯过程回归的均值函数，选择自动相关性确定(ARD)理性平方协函数作为核函数.

对初次循环cycle0的全充数据Dcycle0进行高斯过程回归，计算初始超参数θ.

(4)扩展卡尔曼滤波

对于下一循环cycle=cycle0+1，首先将cycle0次的动力电池全充时间作为cycle循环的初值，也即xcycle(1)W=tcycle0(n0)；然后,导入cycle次的片段充电数据，并开展扩展卡尔曼滤波，具体公式如下.

xcycle(k)=A(k)[xcycle(k-1)]-ΔT+w(k-1)，

(10)

zcycle(k)=GPh[Dcycle0,xcycle(k)]+v(k)，

(11)

式中:A(k)为状态矩阵，文中可将其设为单位矩阵；GPh[D0,xcycle(k)]表示利用Dcycle0数据进行的高斯过程回归并预测xcycle(k)的电压值.

(5)扩展卡尔曼滤波循环递推

预测过程：

(12)

Pcycle(k)′=A(k-1)Pcycle(k-1)A(k-1)T+Q(k).

(13)

利用差商近视雅可比矩阵对模型进行更新：

(14)

更新过程:

(15)

,

(16)

P(k)=[I-K(k)H(k)]P(k)′

.

(17)

式(12)至(17)中，R，Q分别为状态噪声w和测量噪声v对应的协方差.

(6)估算全充时间

由上述过程可知,第cycle=cycle0+1次的全充时间分成两部分：

第cycle次片段充电所用时间，也就是从t1(1)到t1(n1)的时间为ΔT×(n1-1)；

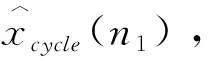
所以，第cycle=cycle0+1次的估算全充时间：

(18)

(7)更新循环

令上一循环cycle=cycle0，将cycle循环的数据作为初始数据，即[(tcycle0(k),Ucycle0(k))]=[(tcycle(k),Ucycle(k))]，且全充时间为xcycle(1),从而可以得到所有循环的估算全充时间

tcycle=xcycle.

(19)

(8)实时估算SOH

(20)

3 纯电动客车数据处理及SOH估算

3.1 纯电动客车数据处理

数据处理主要是通过相关性分析筛选出有价值的数据类型，同时对原始数据中残缺、异常的数据进行补全修正，提高数据质量,进而更加准确的估算SOH.最后得到符合要求的充电片段313个和58 930条完整数据，部分片段数据如表1所示.

表1 停车充电片段筛选划分数据表

3.2 SOH估算

在进行仿真估算前，根据前面所述融合高斯过程回归的扩展卡尔曼滤波SOH算法流程图，还需要对数据进行初始化.目前可知动力电池系统的初始标称容量Co=542 Ah;恒流充电电流I=150 A;U截至=635 V；采样时间间隔ΔT=10 S.由于初次充电全充时间不能直接从数据平台获得，文中拟采用片段充电时间对应的SOC变化来估算全充时间，即对于充电循环的全充时间，采用式(20)进行计算：

x1(0)=t0(n0)-t0(1)/ΔSOC.

(21)

此外，考虑到动力电池刚投入安装使用，车辆下线过程中，测试调试等过程的的不稳定性，容易造成数据失真，文中选择前10次停车充电循环的平均预估全充时间作为循环的全充时间.具体数据如表2所示.由表2求其平均值为13 009.64 s.

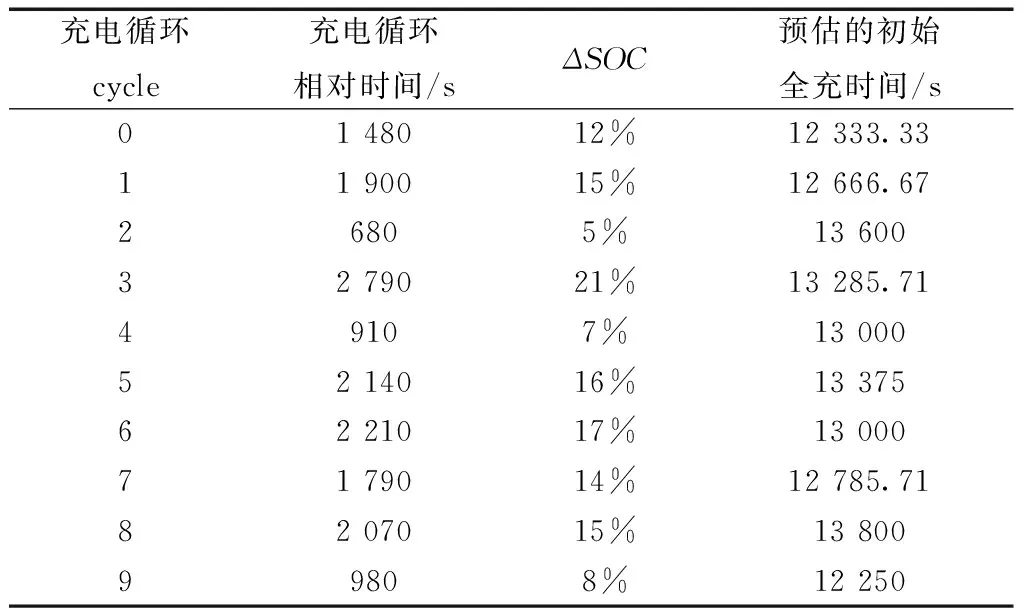
表2 停车充电片段筛选划分数据表

经过上述分析，最后确定将充电循环的全充时间x1(0)=13 010 s.基于文中采用充电容量来估算动力电池健康状态(SOH)的模型原理，由式(22)可知：

.

(22)

由于充电电流I为恒定值，标称容量是固定常数，故估算的动力电池实时容量和健康状态都与每一循环对应的的全充时间成正比.图2-4分别显示了预估的全充时间、预估的当前容量、预估的SOH与循环次数的关系及变化规律.

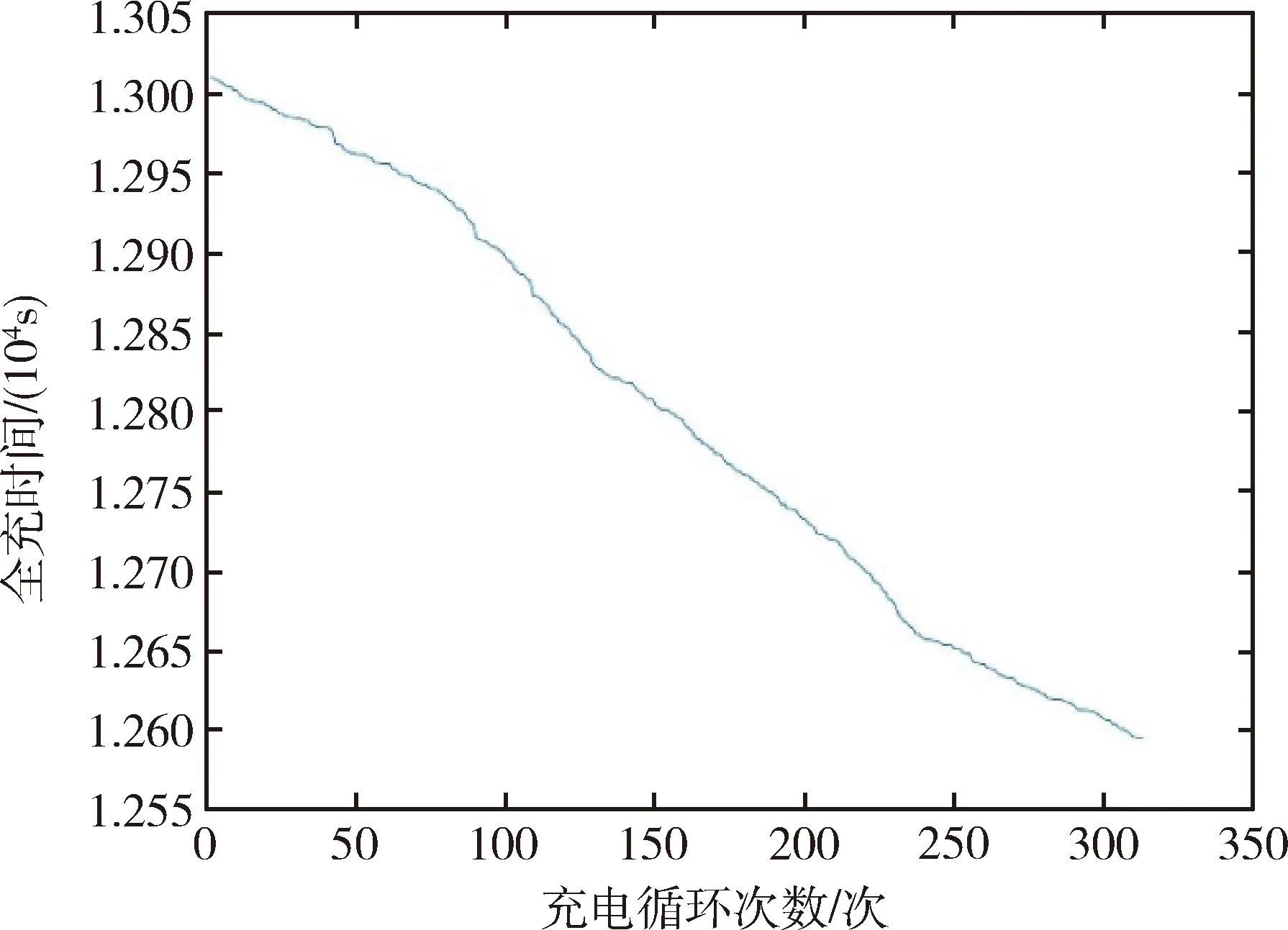
图2 预估的全充时间T与充电循环次数关系图

从图2-4可以看出，在纯电动客车动力电池使用过程中，三者均随着的充电循环次数增加呈现出总体下降、局部波动的趋势，符合实际的纯电动客车动力电池容量和SOH的变化规律；曲线整体较平滑，未呈现较大的波动，说明动力电池系统成组性能和对所有电池单体的不一致性控制较好.其中，有一些循环下降平缓，说明该循环动力电池使用较浅，可用容量变化不大；而另一些循环下降较陡峭，则表明该循环的动力电池放电较深，对健康状态SOH影响较大.

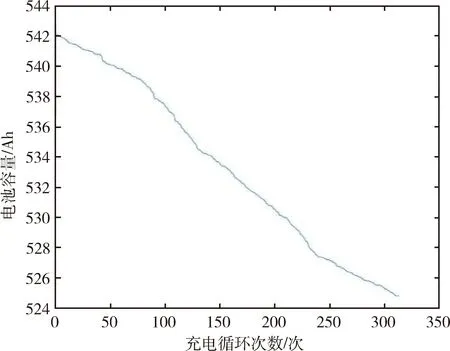
图3 预估的当前容量C与充电循环次数关系图

图4 预估SOH与循环次数关系图

文中选用的磷酸铁锂动力电池系统，是目前国内纯电动客车上应用最广泛的一种电池系统.在经过了300多次充放电循环后，该动力电池预估的全充时间从13 010秒(3.61小时)下降到12 595秒(3.50小时)，可用容量从542 Ah下降到了525 Ah，预估的SOH仍高达97%以上，说明该电池系统具有良好的充放电特性以及很高的健康状态，与实际中该动力电池系统的性能表现相符.

4 实验验证

为了评价文中建立的基于大数据的纯电动客车动力电池SOH估算方法，验证融合高斯过程回归的扩展卡尔曼滤波的SOH模型的性能，通过在2020年6月8日，10月5日，12月30日对所选取的车辆分别进行了动力电池系统充放电实验测试.

通过查询纯电动客车大数据平台可知，2020年6月8日，10月5日，12月30日三天时间所对应的前一充电循还次数分别为第221次，第254次和第312次.通过文中建立的基于大数据的纯电动客车动力电池的SOH估算方法得出的SOH值分别是97.63%，97.23%，96.83%.

文中所得到的充放电实验数据及相关计算结果与使用充电容量预估的SOH值对比如表3和表4所示.

表3 动力电池系统放电测试结果

表4 动力电池系统充电测试结果

文中采用的是基于纯电动客车运行大数据的SOH估算方法，因而预估的SOH误差主要与数据和算法有关.一方面，随着车辆的运行，异常充电数据片段会增加，由于在数据处理过程中对该片段充电数据进行了删除，会导致误差产生；另一方面，在融合高斯过程回归的扩展卡尔曼滤波SOH算法中，某些充电循环对应的充电片段数据量较少，会影响高斯过程回归的精度，进而在扩展卡尔曼滤波中，随着循环递推和迭代的进行，也会导致误差.因此，规范的充电操作，更长的车辆运行时间、更完整的后台采集数据，都可以减少误差的产生，提高SOH的估算精度.对于自带SOH实时计算功能的部分品牌电池BMS，如能将两者数据结合起来进行分析，还可进一步减小SOH的估算误差.

5 结 论

文中以车载终端实时采集的纯电动客车大数据为研究对象，分析了纯电动客车大数据平台采集的实车运行数据特点，提出了采用充电容量代替放电容量来建立动力电池健康状态SOH模型.研究利用了融合高斯过程回归的扩展卡尔曼滤波SOH算法对动力电池SOH进行估算，并且验证了其有效性.对于确保纯电动客车动力电池的安全使用具有一定的价值.由于时间的限制，纯电动客车运行仅一年多时间，得到的数据还不够充分，动力电池后续健康状态SOH的趋势在后续工作中将继续进行实验验证.