多轴联动电火花成形加工的空间摇动方法
2022-07-01孙延鑫褚皓宇奚学程赵万生
孙延鑫,秦 岭,褚皓宇,奚学程,赵万生
( 上海交通大学机械与动力工程学院,机械系统与振动国家重点实验室,上海 200240 )
闭式整体叶盘类零件是航空航天发动机的重要零件, 其零件质量直接影响发动机的可靠性、性能和成本[1]。 多轴联动电火花成形加工具有无宏观切削力、加工性能与材料的机械性能无关、可达性好以及成形精度高等优点,已成为闭式整体叶盘类零件的首选加工方法[2-3]。 闭式整体叶盘类零件的加工常采用浸液加工方式,但冲液条件差,加工过程中形成的金属碎屑、 炭黑等蚀除产物无法及时排出,大幅降低放电稳定性和加工效率,严重制约闭式整体叶盘的产能。
叶盘加工过程中的蚀除产物主要通过冲液、摇动等方式排出。 冲液方式主要有外部冲液和内部充液两种。 其中,外部冲液方式将冲液喷嘴对准叶盘流道放电加工区域,通过油泵将新鲜的工作液射入放电间隙,将放电间隙内带有高浓度蚀除产物的工作液冲出,从而降低蚀除产物浓度,维持极间稳定的放电状态[4]。 外部冲液的排屑效果在加工深度较小时更加显著。 但由于闭式整体叶盘的流道狭长且形状复杂,加工深度很大[5-7],加上放电间隙小,工作液难以通过放电间隙深入放电加工区域排屑[8],外部冲液方式对于闭式整体叶盘加工排屑的改善效果非常有限。
内冲液方式是预先在工具电极上加工冲液孔,通过冲液孔从电极内部将新鲜的高压工作液冲入加工区域,将蚀除产物从放电间隙排出[9]。 相比于外部冲液方式,内冲液方法在加工深度大时仍可将高压工作液射入放电间隙, 具有更好的排屑效果,不受加工深度的限制。 但对于闭式整体叶盘电火花加工而言,成形电极的形状弯曲程度较大,难以在电极上加工冲液孔。 因此,内冲液方式对于闭式整体叶盘的电火花加工也不适用。
在冲液排屑难以适用闭式整体叶盘放电成形加工的情况下,本文采用工具电极摇动的方式促进蚀除产物排出、维持放电稳定性、提高加工效率。 摇动是通过工具电极在伺服进给的同时围绕进给轨迹进行有规律的周期闭环运动[10],带动放电间隙内的工作液流动并在放电间隙形成非均匀流场。 由流体力学知识可知,非均匀流场液体的粘性阻力也是非均匀的, 并且最大间隙处液体的粘性阻力最小、最小间隙处液体的粘性阻力最大,使加工屑更易从最大间隙处排出[11-12],从而可获得理想的极间放电状态。 然而目前针对电极摇动的研究主要集中于单轴进给轨迹的平面摇动方面,而闭式叶盘加工的多轴联动进给轨迹空间摇动的研究十分稀少。 因此,本文以此为背景,研究了多轴联动进给轨迹的空间摇动方法,提高了闭式叶盘的加工效率。
1 工具电极空间摇动方式
工具电极空间摇动示意如图1 所示,工具电极以一定的倾斜角度装夹在夹具上,工件表面相应地倾斜,以保证工具电极轴线垂直于工件表面。 在放电加工时, 工具电极沿着其轴线方向伺服进给,同时工具电极中心在垂直于轴线的平面内进行圆周运动,该运动即为本文研究的空间摇动。

图1 工具电极空间摇动示意图
工具电极空间摇动带动放电间隙内的工作液流动并在放电间隙形成非均匀流场,促进加工屑从最大间隙处排出,降低间隙内蚀除产物含量,保证极间正常放电状态,提高电火花成形加工效率。
2 工具电极空间摇动运动学
本文使用五轴联动电火花成形加工机床。 工件安装在B、C 轴旋转工作台,通过工作台的旋转使其定位在加工位姿; 工具电极垂直于工件表面安装,通过机床的X、Y、Z 三轴带动其完成伺服进给和空间摇动。 机床的串行运动链见图2。

图2 五轴联动电火花成形加工机床的串行运动链
在工具电极空间摇动的运动学推导过程中,依据机床的串行运动链建立了机床坐标系、工件坐标系和刀具坐标系。因为在放电加工的过程中只有X、Y、Z 三轴带动工具电极运动,机床B、C 轴只起到工件与刀具的定位作用, 在放电加工过程中并不运动,所以在初始状态下可将刀具坐标系视为与机床坐标系重合,只需研究工件坐标系与机床坐标系之间的向量转换关系即可。 工件坐标系与机床坐标系的向量转换关系为:

式中:gmw(θ)是用于将工件坐标系中的向量qew转化为机床坐标系中的向量qem的转换矩阵。 其中,θ=θi;θi=θx,θy,θz,θa,θb,θc;i=x,y,z,a,b,c,为直线轴X、Y、Z和旋转轴A、B、C 相对于初始状态的位移和角位移。
工具电极空间摇动的实现思路为:求解工件坐标系下的空间摇动向量,先使用转换矩阵gmw(θ)将其变换得到机床坐标系下的空间摇动向量,再将插补周期内的空间摇动进给量按照机床坐标系下的空间摇动向量分解到各个运动轴后得到插补周期内X、Y、Z 三个运动轴的进给量,进而控制运动轴实现工具电极的空间摇动。
2.1 转换矩阵gmw(θ)的求解
根据图2,工件坐标系由机床坐标系绕B 轴、C轴旋转得到。根据旋量理论,转换矩阵gmw(θ)为初始状态下的旋转矩阵gmw(0)、C 轴的旋转矩阵eω^cθc和B轴的旋转矩阵eω^bθb的乘积,即:

初始状态下工件坐标系与机床坐标系的关系如图3 所示, 工件坐标系Ow-XwYwZw相对于机床坐标系Om-XmYmZm无角位移,根据旋量理论初始状态下的旋转矩阵gmw(0)为单位阵I3×3。

图3 初始状态下的机床坐标系与工件坐标系
θb、θc分别为机床坐标系绕B 轴、C 轴旋转的角度,即工件姿态角;为斜对称矩阵,可由B 轴、C 轴的单位矢量ωb、ωc计算得到。 对于单位矢量ω=(ω1ω2ω3)T,斜对称矩阵根据图4,ωb=(0 1 0)T、ωc=(0 0 1)T,则计算出B 轴、C 轴的斜对称矩阵

图4 机床坐标系
根据Rodrigues 公式,即:

可计算B 轴、C 轴的旋转矩阵,将ω^b、ω^c、θb、θc代入式(3),可得:


故工件坐标系到机床坐标系的转换矩阵为:

2.2 机床坐标系下的空间摇动向量求解
如图5 所示,工件坐标系下的空间摇动圆位于平面X′OY′内,平行于工件表面。O 点为空间摇动圆的圆心,n′是空间摇动平面的单位法向量,s′为空间摇动的单位位置向量,n′与s′的叉乘即为工件坐标系下的空间摇动向量,即:

图5 工件坐标系下的空间摇动向量
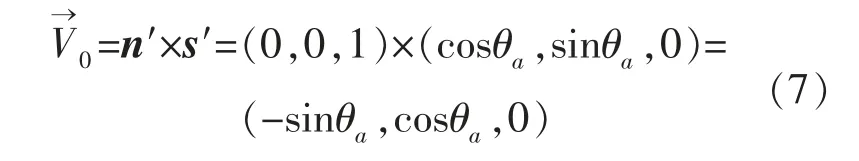
式中:θa为空间摇动的进程角,代表工件坐标系下当前时刻工具电极在空间摇动圆中的位置。


图6 机床坐标系下的空间摇动向量
将转换矩阵gmw(θ)和工件坐标系下的空间摇动向量的表达式,即将式(6)、式(7)代入式(8),计算得到机床坐标系下的空间摇动向量(a,b,c):

2.3 插补周期内机床各轴运动分量的求解
已知摇动速度v、摇动半径r 和插补周期T,可求得插补周期内空间摇动的角增量θa0,即:

对角增量θa0进行积分计算,即可求得空间摇动的进程角θa,即:

已知θc、θb,即可通过式(9)求得机床坐标系下的空间摇动向量V→(a,b,c),同时可求得插补周期内空间摇动的进给量s, 即摇动速度v 和插补周期T的乘积为:

将插补周期内空间摇动的进给量s 按照机床坐标系下的空间摇动向量V→(a,b,c)分解到X、Y、Z 三个运动轴,即可得到插补周期内三个运动轴的空间摇动进给量x、y、z 为:


综上所述,V→的模长为1,可将式(13)简化为:

结合式(10)、式(11)和式(15)可知,已知摇动速度v、 摇动半径r、 插补周期T 和工件姿态角θc、θb,即可求得插补周期内X、Y、Z 三轴的空间摇动进给量x、y、z,从而控制机床完成空间摇动。 将空间摇动与伺服进给运动相结合,即可在工具电极放电加工的同时通过空间摇动促进放电间隙内蚀除产物排出、维持理想放电状态、提高成形加工效率。
3 仿真验证
仿真验证的思路是在建模软件中模拟工具电极的伺服运动和空间摇动混合轨迹,通过比较不同工件姿态下的工具电极运动轨迹,验证空间摇动控制方法的正确性。
图7 和图8 是在伺服进给速度vs=100 μm/s、摇动半径r=1000 μm 而工件姿态角θc、θb分别均为0°、45°时的工具电极伺服运动和空间摇动轨迹。 其中,图7a 和图8a 所示工具电极运动轨迹分别由图7b、图7c 和图8b、图8c 所示伺服运动轨迹和空间摇动轨迹叠加而成。

图7 θc=0°、θb=0°时的工具电极运动轨迹

图8 θc=45°,θb=45°时的工具电极运动轨迹
图7 中工件姿态角θc、θb均为0°, 此时刀具在Z-方向伺服进给, 同时在XOY 平面内进行常规摇动,刀具轨迹为Z-方向的等距螺旋线。 图8 中工件姿态角θc、θb均为45°,由图8b 可知,此时刀具进行空间线段的伺服进给, 同时在图8c 所示的与空间线段垂直的平面内进行摇动,其刀具轨迹为伺服运动方向的等距螺旋线。
由以上仿真结果可知,本文研究的空间摇动方法可同时实现工具电极的伺服运动和空间摇动,且伺服运动方向与空间摇动平面垂直,两者叠加即可获得预想中的螺旋形工具电极运动轨迹。 在工件姿态角θc、θb为0°时, 工具电极可进行Z-方向的螺旋运动,这也证明本文的空间摇动方法对于常规摇动的普适性。
4 结束语
本文提出了一种多轴联动电火花成形加工的工具电极空间摇动方法,基于螺旋理论推导了工具电极空间摇动运动学公式,可计算得到插补周期内各个运动轴的坐标增量,为控制电火花成形加工机床运动轴实现工具电极的空间摇动提供了理论基础。 并进行工具电极运动轨迹仿真,印证了该方法的正确性和合理性。
