机床与工件相对运动对去除函数形成稳定性的影响机制研究

杨航，管瑞，黄文，何建国

（1.遵义师范学院 工学院, 贵州遵义 563006；2.中国工程物理研究院 机械制造工艺研究所, 四川绵阳 621900）

磁流变抛光技术将电磁理论，流体力学，分析化学等运用于光学元件表面加工[1]。其具有去除函数稳定，面形精度高等优点[2]。徐超等[3]对磁流变抛光去除函数建模并研究曲面曲率变化对去除函数的影响，路家斌等[4]研究了磁场分布对多磨头磁流变抛光材料去除的影响，宋辞等[5]利用加工前后的面形误差分布和仿真计算的面形残差分布，建立磁流变抛光的去除函数预测模型。磁流变抛光是在梯度磁场作用下[6]，利用磁流变抛光液转变为具有粘塑性的Bingham介质[7]，在抛光轮与工件之间的间隙形成一段凸起的“柔性抛光磨[8]”，柔性抛光缎带与工件表面接触且被工件压入一定深度，形成抛光斑[9]，对工件表面的材料进行去除。MRF去除函数定义为单位时间内柔性缎带驻留在工件同一位置时材料的去除量分布[10]。去除函数稳定性是指在单个加工周期内材料去除效率的稳定程度，其受多种因素影响，在连续加工状态下呈下降趋势，由磁流变液所致[11]。此外，磁场强度、工件硬度、抛光时间等都会对去除函数的稳定性形成影响[12]。然而对于去除函数的稳定性机制的研究还是缺乏的。而运用机床与工件之间形成的相对运动研究去除函数形成的稳定性，主要是通过分析在抛光区域工件不同速度使工件表面受到的压力不同，压力作用对工件表面材料进行去除，形成去除函数，压力稳定，去除函数达到稳定。

1 机床与工件相对运动对去除函数形成稳定性的表征

1.1 磁流变抛光机床与工件相对运动的去除机理

在磁流变抛光机床中，主要由抛光轮、磁流变液、励磁装置和运动盘相互作用对工件表面进行抛光，如图1所示。其中，抛光轮端面平行XOZ面绕穿过d点的定轴转动，磁流变液附着在抛光轮上，在磁场作用下磁流变液转变成粘塑性Bingham介质，在工件与抛光轮的间隙之间凸起为一段柔性抛光缎带，运动盘固定工件与柔性抛光缎带在抛光区域接触并嵌入一定深度形成抛光斑，随着工件与抛光轮之间的相对运动，磁流变液形成的抛光缎带对工件表面产生一定的压力，工件表面的材料在压力作用下被去除形成去除函数。而工件表面受到的压力主要由流体动压力，磁化压力组成。

图1 机床与工件相对运动的去除模型

对工件表面受到的流体动压力的求解满足雷诺方程。当工件在XOY平面做平动，设工件上某点在X轴方向的速度矢量为 νx，在Y轴方向的速度矢量为 νy， 抛光轮在抛光斑处的线速度矢量为 νp，抛光轮与工件上的点的相对速度矢量由 ν表示，即

抛光轮在抛光斑的线速度为

式中：r为抛光轮的半径；ω为抛光轮角速度。

抛光轮与工件上的点的相对速度可表示为

工件表面上某一点到抛光轮上的距离h表示为

式中：h0为工件表面与抛光轮之间的最小间隙；x为工件表面上的点的横坐标值。由动压润滑原理知，当工件在XOY平面沿X轴方向运动，假设流体动压力在Y轴方向的变化率一定，雷诺方程可简化为

式中：dPd(x，y)/dx表示动压力在X轴方向的变化率；η为磁流变液的初始黏度；为工件表面受到极大值压力点到抛光轮的间隙高度。由工件平动的几何模型和边界条件求得

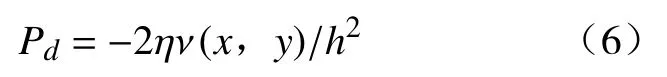
同理，可求出工件在XOY平面沿Y轴方向运动的流体动压力。

当工件在XOZ平面绕e点以半径R摆动，摆动线速度矢量为 νr，工件上的点与抛光轮的相对速度ν1表示为

工件摆动的线速度为

式中：R为工件摆动半径；ωr为工件摆动角速度。当工件摆动θ弧度时，工件表面上的点与抛光轮的相对速度ν1(θ)表示为：

工件摆动时的流体动压力为

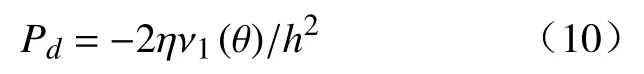
磁化压力与外加磁场的大小和工件嵌入深度有关，对于平面工件，工件做平动和摆动都是对柔性缎带的嵌入深度不变，磁场强度不变，所以磁化压力对于平面工件的运动为定值。

机床与工件相对运动的去除机理是工件的运动方式和运动速度使得其与抛光轮产生相对运动速度，工件与抛光轮之间的流体产生流体动压力，而磁场对磁流变液产生磁化压力，在抛光区域对工件表面产生压力作用，从而对工件表面的材料进行去除。

1.2 去除函数形成稳定性的表征

平面工件与机床的相对运动对去除函数的稳定性影响主要由压力在抛光斑的分布决定。抛光斑是在工件表面与抛光轮之间的间隙内，磁流变液在梯度磁场下形成的Bingham介质流体与工件表面接触并被压入一定深度而形成的，其形状如图2所示。去除函数是在抛光斑中，工件表面受到的压力对表面材料进行去除而形成。

图2 机床与工件相对运动形成的抛光斑形状

去除函数的稳定性是机床与工件相对运动时，抛光斑中工件表面受到的压力分布在抛光斑长度上的稳定程度。假设工件以不同运动速度沿X轴方向运动，在X轴上工件表面各点所受的压力不同。即在对应的s上，不同运动速度的工件表面都存在不同的压力值。抛光斑的长度为L,当工件为初始状态时，工件表面压力在抛光区域长度L上的压力均值为μ0，当工件运动时，工件不同运动速度或摆动弧度产生的压力均值为μi，去除函数的稳定性Δ表示为：

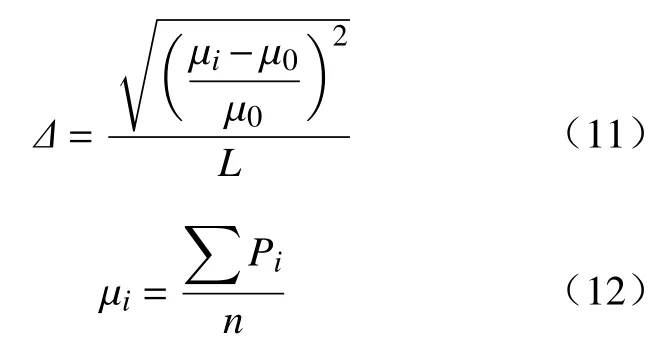
式中：i代表工件以某一个运动速度或摆动弧度对应的压力最大值和压力最小值；n代表在s上压力值分布的数量；Δ值越小，工件表面的压力越稳定，去除函数越稳定。

2 机床与工件相对运动对去除函数形成稳定性的仿真试验

2.1 试验设计

在磁流变抛光过程中，为了达到工件表面的形面要求，提高抛光过程中工件的抛光速度，因此合理设置机床与工件的相对运动速度是有必要的。但是，工件不同的运动速度以及摆动速度会对去除函数的稳定性产生不同的影响。通过试验，利用FLUENT仿真得到抛光区域的压力，利用速度对压力的实验结果进行系统的分析，最终分析磁流变抛光过程中去除函数稳定性的稳定机制。

在磁流变抛光中，磁流变液充当介质的作用使工件与其接触时工件表面的材料被去除，因此对磁流变液需要进行密度和黏度的选取。在本试验中，磁流变液的初始密度为 0.375 5 kg/m³，由于磁流变液在梯度磁场下成核区域的Bingham介质的粘度可近似由Herschel-Bulkley模型的参数代替，故采取表1所示的Herschel-Bulkley模型参数进行试验。

表1 Herschel-Bulkley模型的参数选定

实验分为两组，第1组工件在XOY平面沿X轴方向和沿Y轴方向运动，且两个方向的实验数据相同，如表2所示。实验进行到第11次，在其他参数不变的情况下，通过分别改变工件在X轴和Y轴方向的运动速度分析去除函数的稳定性。

表2 工件在X轴和Y轴方向运动对去除函数稳定性影响的实验参数

第2组是工件以相同的摆动速度绕定轴摆动，如表3所示。实验同样进行第11次时，通过工件不同的摆动弧度使机床与工件之间产生相对运动，研究去除函数的稳定性。

表3 工件摆动对去除函数稳定性影响的实验参数

2.2 工件在XOY平面平动对去除函数稳定性的影响

1）当工件在XOY平面沿X轴方向运动，不同的运动速度得到工件表面受到的压力在抛光斑中的分布以及最大压力值和最小压力值，如图3所示。

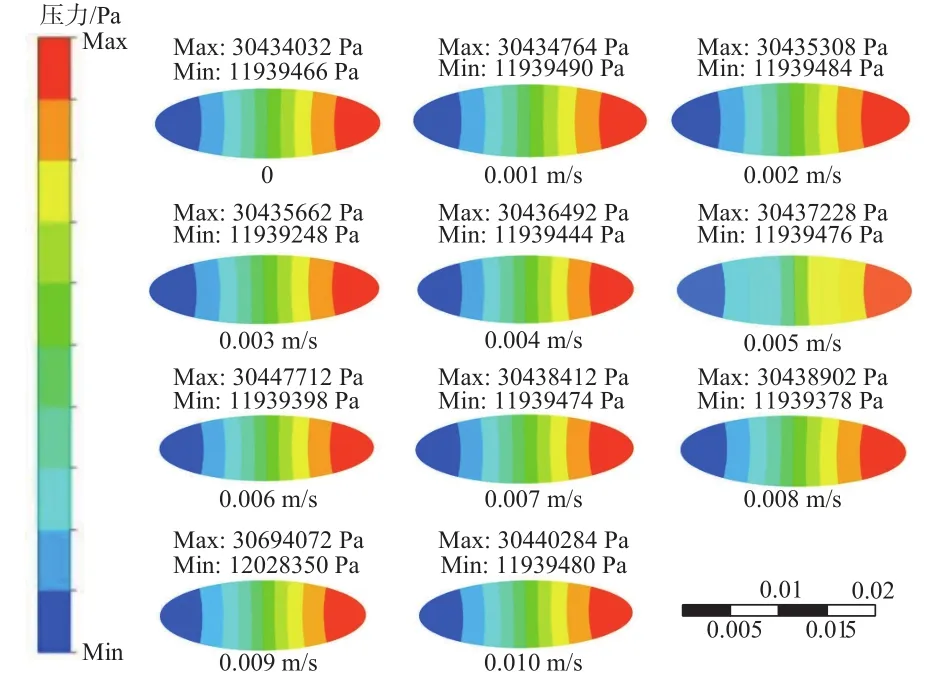
图3 工件在 X 轴方向 0 ~ 0.01 m/s形成的去除函数压力云图

当工件静止时，压力为稳定的，抛光区域的压力最大值出现在抛光刚开始时的进口处，压力最小值出现在出口处，因为工件静止，在抛光区域抛光轮的切向速度使工件与抛光轮之间的流体对工件表面产生压力，工件表面的材料被去除，当抛光一段时间，工件表面的压力减小，所以导致抛光区域压力从进口到出口逐渐减小。而当工件沿X轴方向运动，不同速度对应抛光区域的压力相对与工件静止时的压力发生改变，所以去除函数的稳定性发生改变。将仿真实验得到的压力数据转换为压力在抛光斑s上的分布曲线图，如图4所示。

图4 工件在 X 轴方向 0~ 0.01 m/s的压力在抛光斑长度s上分布

由图4，工件静止时的压力在抛光区域长度线上压力最大值最小，压力最小值处于工件速度为0.004 m/s和0.007 m/s之间。工件运动速度分别为0.004 m/s、0.006 m/s、0.008 m/s、0.003 m/s 时的压力最小值都小于工件静止时的压力最小值，其余工件运动速度对应的压力最小值均大于工件静止时的压力。而工件运动速度为0.009 m/s时，工件压力最大值和最小值都是最大的。由于磁流变抛光液以非紧密固结的方式附着在磁流变抛光轮上，当速度变化范围不大时，其通过滑移传导的速度关系对流场速度影响较弱。因而不同转速下压力分布接近。将实验得到的压力数值进行分析，得到图5所示的工件不同运动速度对应的去除函数稳定性变化图。

图5 工件在 X 轴方向 0 ~ 0.01 m/s的去除函数稳定性

图5中，当工件静止时，去除函数最稳定，随着速度的增大，Δ值越大，所以去除函数越不稳定。而工件运动速度为0.009 m/s时，去除函数的稳定性发生突变，达到最不稳定的状态，显然在抛光时这个速度是不能采用的。不考虑速度极值时的稳定性数值畸变，流场在低速情况下具有更好的稳定性，对磁流变抛光加工的确定性更高。

2）同样是在XOY平面内，当工件X轴方向的速度大小为零，工件沿Y轴方向以不同速度运动，实验得到工件表面压力在抛光区域的分布如图6所示。

图6 工件在 Y 轴方向 0 ~ 0.01 m/s形成的去除函数压力云图

图6中，虽然工件只是沿着Y轴方向运动，但是抛光轮的切向速度还是沿着X轴方向，所以工件表面受到的压力也是进口处的压力最大，从进口到出口，压力逐渐减小。将压力数值转化为压力数据转换为压力在抛光斑s上的分布曲线图，如图7所示。

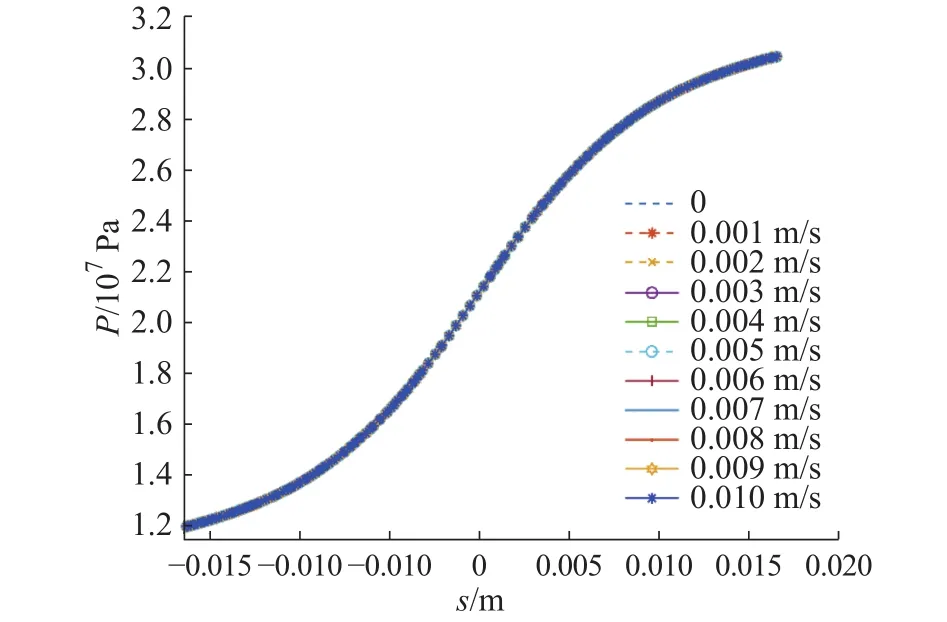
图7 工件在 Y 轴方向 0 ~ 0.01 m/s的压力在抛光斑长度s上的分布

图7中，工件在Y轴上的运动速度为0.009 m/s时，工件表面受到的压力最大值和最小值是最小的，而其他运动速度使工件表面受到的压力最大值和最小值交替分布，这是因为抛光轮速度的方向和工件的运动方向不同，抛光轮与工件之间的流体受到两个方向的流体动压力，使工件表面的材料被两个方向的压力同时去除。在Y方向其几何尺度虽然较X方向有所变化，可以看出，其受到流速变化引起的去除函数波动规律与X方向具有一致性。将工件表面受到的压力分析得到图8所示的工件在Y轴方向运动去除函数的稳定性变化图。

图8 工件在 Y 轴方向 0 ~ 0.01 m/s的去除函数稳定性

图8中当工件运动速度为0时，去除函数最稳定，当速度逐渐增大，去除函数的稳定性在波动。虽然去除函数稳定性都在减小，但是去除函数的稳定性是先减小再增大这样往复。所以，当工件在Y轴方向运动时，随着工件运动速度的增大，去除函数的稳定性是在一定速度范围内波动的。由于Y方向几何尺度较小，其数值波动在同等量级下，表现出更高的变化梯度，因此其波动性增强，稳定性下降。

2.3 工件摆动对去除函数稳定性的影响

工件摆动和工件平动不同，随着工件摆动弧度变化，工件与柔性抛光缎带的接触位置也会随之变化。工件在抛光区域长度上工件不同摆动弧度压力的分布如图9所示。

图9 工件摆动 0.472 ~ 0.528 rad形成的去除函数压力云图

由于工件摆动的线速度方向与抛光轮的线速度方向相同，同样在抛光区域的进口处压力最大，出口处的压力最小。工件的摆动弧度不同得到图10所示的压力数据转换为压力在抛光斑s上的分布曲线图。

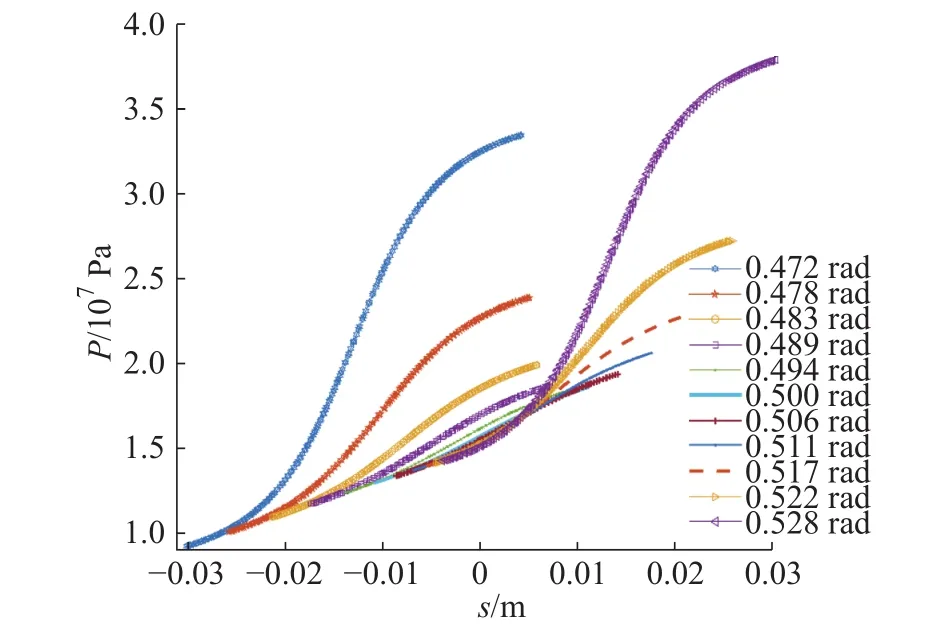
图10 工件摆动 0.472 ~ 0.528 rad 的压力在抛光斑长度s上的分布

由图10可知，工件的摆动弧度不同，抛光区域的长度不同，工件偏离抛光轮与工件中心连线角度越大，抛光区域的长度越大。抛光区域的压力最大值从 0.472 rad 到 0.500 rad 逐渐减小，从 0.500 rad到0.528 rad逐渐增大。工件摆动弧度为0.472 rad是压力最小值最小，0.528 rad是压力最小值最大。工件摆动对于流场的波动影响是复杂的，因为旋转运动可以同时改变所有位置的流场，可能引入漩涡，引起流场畸变。去除函数的稳定性如图11所示。

由图11 知，当工件摆动在 0.472 ~ 0.500 rad 内，去除函数的稳定性先增大然后减小再增大到最稳定，其中在 0.483 ~ 0.489 rad 内去除函数稳定性会产生一个波动，这个波动是由于抛光轮是特定的形状，工件摆动为0.483 rad时工件表面受到的压力均值小，而在0.489 rad时工件表面受到的压力均值大，导致突变；工件摆动在 0.500 ~ 0.528 rad 区间内，去除函数的稳定性逐渐减小。可以看出，摆动对于去除函数流场稳定性的影响是以非线性的方式发生的。这与流场内禀结构有直接的关系。

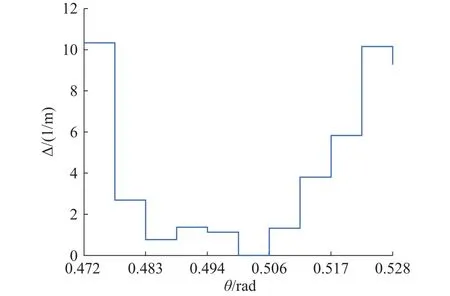
图11 工件摆动 0.472 ~ 0.528 rad 去除函数的稳定性

3 结论

1）当工件在X轴上运动，速度越大，去除函数越不稳定，但是工件运动速度是在一定范围内，速度太大，去除函数的稳定性会发生突变。

2）当工件在Y轴方向运动，去除函数在工件的运动速度范围内产生波动，因此在抛光的时候，应当选取去除函数较稳定的速度进行抛光。

3）当工件在XOZ平面摆动时，工件的位置在0.500 rad时的初始状态，去除函数最稳定，当工件摆动在 0 ~ 0.500 rad 时，弧度值越小，去除函数越不稳定；工件摆动大于0.500 rad时，去除函数的稳定性逐渐减小。因此，工件的摆动弧度需要控制在其摆线与工件初始位置时的夹角较小，才能保证抛光去除函数的稳定性较高，得到面形精度更高的工件。