某船闸枢纽主要分区渗透参数敏感性及反演分析
2022-06-30金洪杰沈振中杨金孟孙一清张文兵
金洪杰,甘 磊,沈振中,2,杨金孟,孙一清,张文兵
(1.河海大学 水利水电学院,江苏 南京210098;2.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)
1 研究背景
渗流问题是水利工程设计和建设中需重点研究的问题之一,水工程渗流安全不容忽视[1-2]。船闸是水利枢纽中的主要通航建筑物,其服役期间,闸门前后水位升降、地下水位变化、潮汐、洪峰、泄洪等过程均会对船闸及岸坡的渗流稳定及结构安全产生影响[3]。此外,在长期水头差的作用下,船闸地基及岸坡岩土体中会产生渗透水流,从而增大基底扬压力,影响船闸闸基的稳定[4]。研究船闸渗流特性具有重要的工程价值和理论意义[3-5],而各分区材料渗透参数的确定是渗流分析的前提。目前,渗透参数的获取方法主要有3种:地质勘测、试验测定和反演分析。近年来,反演分析方法已成为确定材料渗透参数的有效手段之一[6]。
渗流参数反演按求解问题不同,可分为解析法、图解法和数值法[7]。其中数值法应用最为广泛[7-10],如:何吉等[7]采用渗流有限单元法,开展了单孔压水试验的数值模拟,结合BP神经网络的非线性映射能力,提出了单裂隙岩体渗透张量的反演分析方法;Gan等[8]基于等效连续渗流介质模型,提出了一种反演破碎裂隙岩体渗透系数的新方法,并将反演所得岩体渗透系数应用于甘肃省上磨水库坝区渗流场分析;黄铭等[9]基于ANSYS软件进行二次开发,采取分层搜索法反演得到材料渗透系数,实现了海堤工程的渗流仿真。
参数反演过程中涉及的参数组合及监测数据较为繁杂,定量研究各参数变化对监测指标的影响具有重要意义。敏感性分析是一种定量表征相关因素影响程度的有效方法,其在工程渗流领域被广泛采用[10-13],如:王学武等[11]以某高坝上游土石围堰为研究对象,分析了两岸岩体和防渗墙渗透系数对基坑渗流量的影响,结果表明两岸岩体和防渗墙渗透系数对基坑渗流量的敏感性较高;周青等[12]结合阿青水电站心墙坝工程,对坝壳料、覆盖层和心墙的渗透系数进行了单因素敏感性分析,明确了各主要坝料渗透系数对坝体渗流场的影响程度;周邠鹏等[13]针对黑河金盆水库工程,开展了心墙、帷幕及两岸岩体等材料渗透系数敏感性分析,结果表明帷幕和两岸岩体的渗透系数对坝区渗流场的敏感性较高,在渗流控制及优化设计时需重点关注。本文以某大型船闸为研究对象,建立该船闸三维渗流有限元分析模型,针对船闸混凝土闸体、基岩、防渗帷幕和排水孔幕的渗透系数开展正交试验设计,研究各分区材料渗透系数对船闸渗流场的影响程度,据此进一步开展船闸主要分区材料渗透系数反演分析,以期为类似工程渗流分析评价提供借鉴。
2 渗流分析的基本原理
2.1 渗流计算
本文采用三维渗流有限元计算分析程序[14-16]对所研究的船闸的渗流性态进行计算分析,渗流有限元微分控制方程如下:
(1)

该微分方程的定解条件可分为两种:
(1)初始条件:
hc(xi,0)=hc(xi,t0) (i=1,2,3)
(2)
(2)边界条件:
hc(xi,t)|Γ1=hc1(xi,t)
(3)
(4)
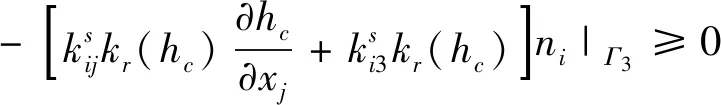
(5)
式中:t0为初始时刻,s;hc1为已知水头,m;ni为外法线方向余弦;Γ1为已知水头边界;Γ2为已知流量边界;qn为已知流量,m3/s;hc(t0)为初始t0时刻的渗流场水头,m;Γ3为逸出边界。
2.2 参数敏感性分析
通过计算获得船闸渗流场的水头分布,得到各节点计算水位H。由于地下水水位分布在一定程度上可反映船闸渗流性态,因此将其作为指标进行船闸渗流场的敏感性分析。
本文采取“正交试验设计”的方法进行因素组合设计[17],开展不同方案下船闸三维有限元渗流反演分析。通过对试验结果的极差和方差分析,筛选出对船闸基础地下水水位敏感性较高的分区渗透系数作为后续反演分析的重点对象,以提高反演效率。
(1)极差分析。采用极差大小衡量关键指标对相关因素的敏感程度,其具体计算公式如下:
(6)
Rj=max{K1j,K2j,…,Knj}-min{K1j,K2j,…,Knj}
(7)
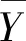
(2)方差分析。方差分析主要用来研究因素和指标之间的相关性,判断其影响是否显著。F值为方差分析中评判显著性水平的统计量值。通过比较F值,可得到各因素对指标影响程度的大小;查询F检验表,可判断该因素对指标的影响是否显著。具体公式如下:
(8)

3 工程实例
3.1 工程概况
某船闸布置于枢纽左侧宽阔的弓形凸岸。船闸基岩为新鲜花岗岩,无风化层及软弱地基;闸墩之间及两侧强风化和弱风化岩体均已被挖除,并以回填混凝土加固。船闸上游面水库属于典型季节型调节水库,水位变化较为频繁,2019年10月28日至2019年12月31日期间,库水位变化较为稳定,平均库水位为174.35 m,最大变幅为1.15 m。从左岸山体段经左侧挡水坝段、两线船闸及右侧挡水坝段的基础灌浆廊道至右侧的中间山体连接段,布置有1个监测横断面,横断面位于帷幕和孔幕之间,共布置17支测压管,可实现船闸及边坡山体地下水水位的实时监测。
3.2 有限元模型
结合该船闸工程的水文地质条件和监测点分布情况,建立三维渗流有限元计算模型。选取模型边界范围如下:下边界截取至闸室底板建基面向下延伸60 m;下游边界截取至与闸室段连接处;左、右两岸从闸室外侧开始,分别向两侧延伸3倍闸室宽度,即100 m。模型采用笛卡尔坐标系,具体定义如下:x轴平行于闸轴线,由左岸指向右岸;y轴顺河流方向,指向下游,取船闸与水库交界处为y轴零点;z轴垂直于地平面,指向上方,与实际高程一致。
综合船闸计算区域内地形地质和建筑物结构等特征,建立船闸及地基三维有限元渗流分析模型。沿模型y轴方向选取了11个控制断面,包含闸室、防渗帷幕和排水孔幕结构体断面等。模型结点总数为21 644个,单元总数为19 875个。船闸整体有限元模型及网格剖分如图1、2所示。
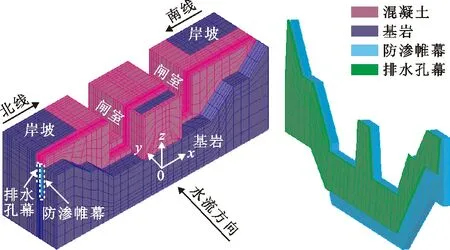
图1 船闸三维有限元模型及网格剖分示意图
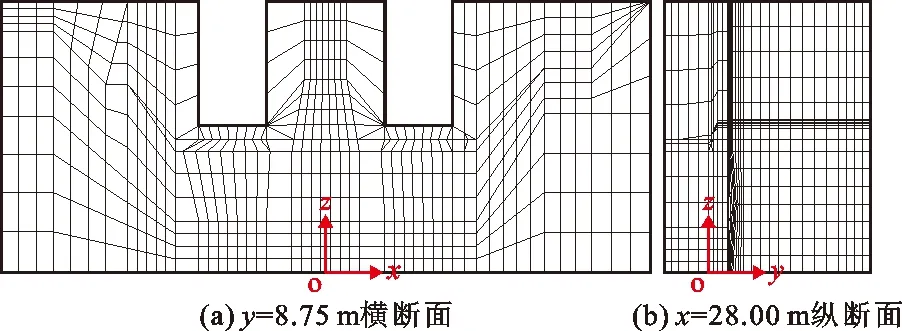
图2 船闸三维有限元模型横、纵断面网格剖分示意图
3.3 反演参数及边界条件
结合水文、地质勘测数据及监测资料,初步设定船闸模型各分区(混凝土、基岩、防渗帷幕、排水孔幕)渗透系数k的数值反演范围,具体见表1。设定左、右边坡地下水水位分别为200.00、220.00 m,反演库水位为174.35 m,该水位所处时间段水库水位变化幅度较小,船闸渗流场较为稳定,反演结果更准确。从渗流监测纵断面中选取6个典型测点在反演时段的平均水位为约束条件,测点钻孔分布于南、北线边坡、闸室及闸墩6个不同的闸段,各测点监测数据稳定、完整。6个典型测点分布及其反演时段测压管水头分别如图3和表2所示。

表1 船闸模型各分区材料渗透系数值反演范围 cm/s

图3 6个渗流监测典型测点分布示意图(单位:m)
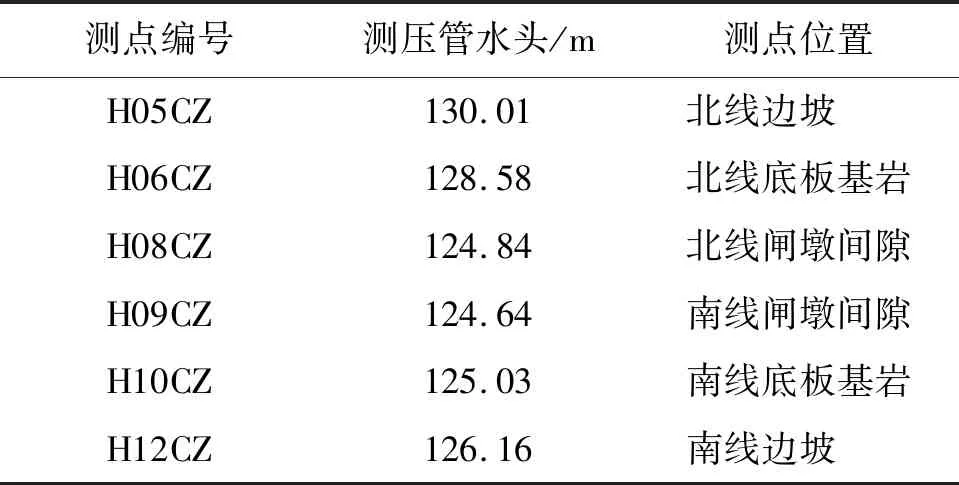
表2 库水位为174.35 m时6个典型测点的测压管水头
模型计算边界主要有3种,分别为已知水头边界、不透水边界和出渗边界。具体设置如下:已知水头边界为水库蓄水位和左、右岸地下水水位以下的给定水头边界,包括挡水面、闸室内的闸墩壁面和排水孔幕顶端;出渗边界主要为基岩内的排水廊道;不透水边界为模型底边界。
4 敏感性分析
4.1 正交实验设计
选取上述6个典型测点水头值作为计算分析的考察指标,分别标记为H5、H6、H8、H9、H10和H12;以混凝土、基岩、帷幕和孔幕4种分区的渗透系数为因素,设计正交实验。结合地勘报告及相关工程经验,设定1组材料渗透系数基准值为1.05×10-7、6.75×10-6、2.92×10-6和2.49×10-4cm/s,在此基础上分别增大和减小20%模拟高、中、低3个因素水平[18];不考虑各因素之间的交互作用并剔除等比例的渗透系数组合。根据实验因素和水平数,选择L9(34)正交试验表,确定的因素水平次序见表3,正交试验方案及结果见表4。
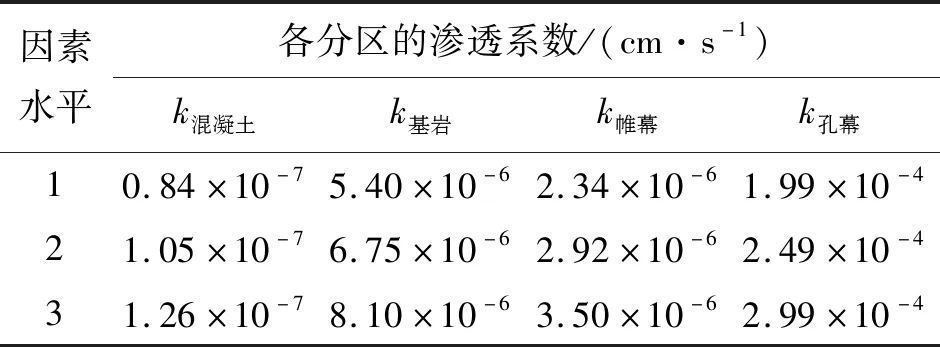
表3 船闸渗流场敏感性分析的因素与水平

表4 船闸渗流场敏感性分析L9(34)正交试验方案
4.2 极差分析
各典型测点水头指标Hi的极差分析结果如图4所示。由图4可知,混凝土、基岩、帷幕和孔幕4种分区的渗透系数对6个典型测点水头值的敏感性高低排序相同,均为k帷幕>k基岩>k孔幕>k混凝土;由此判断该4种材料中帷幕渗透系数的改变对船闸渗流场的影响最大,其次分别为基岩、孔幕和混凝土的渗透系数。

图4 船闸渗流场影响因素极差对比
为进一步研究各因素对不同测点地下水水位影响权重的变化规律,本文对极差计算结果进行归一化处理,结果见表5。由表5可知,各测点帷幕和混凝土的渗透系数对船闸地下水水位的影响权重变化幅度较小,孔幕的渗透系数影响权重随测点位置的改变其变化幅度较为明显,呈现中轴线附近大两侧小的分布趋势。
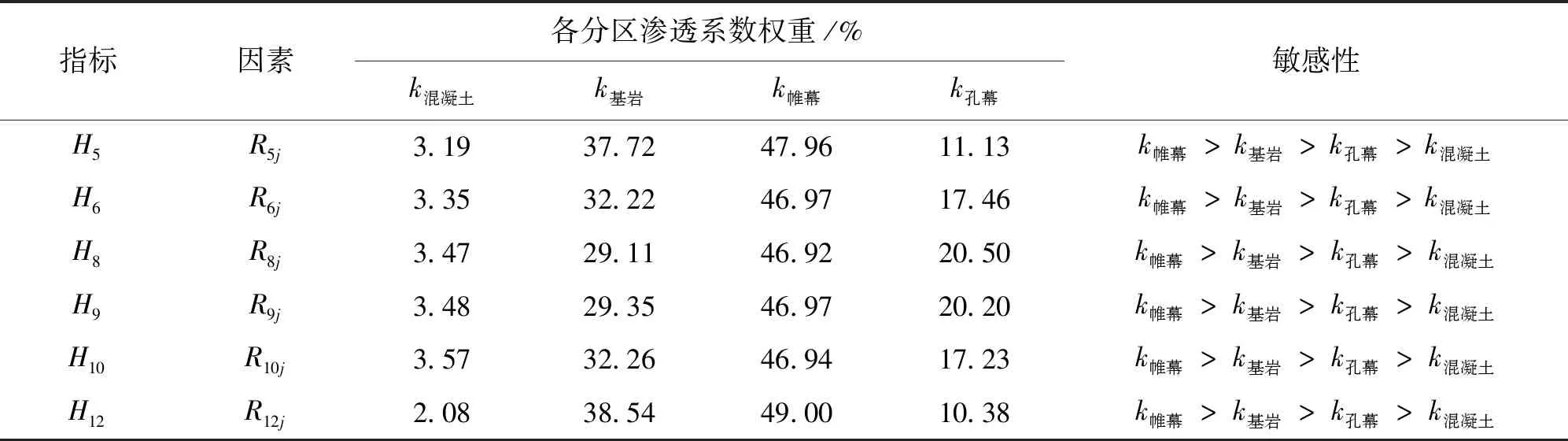
表5 各典型测点指标Hi极差的归一化分析结果
4.3 方差分析
通过极差分析对各因素的敏感程度进行了排序,结合方差分析进一步剖析试验结果,以验证极差分析结果的合理性,判断各因素对指标的影响是否显著。其分析结果见表6。
由表6可知,各因素对6个指标的显著性水平分布规律相同。结合各因素Fij值判断,其对Hi影响的显著性水平大小排序为k帷幕>k基岩>k孔幕>k混凝土,其中k帷幕和k基岩对Hi的影响显著,敏感性较高;k孔幕对于Hi的影响次之,敏感性一般;k混凝土对于Hi的影响不显著,敏感性较低。
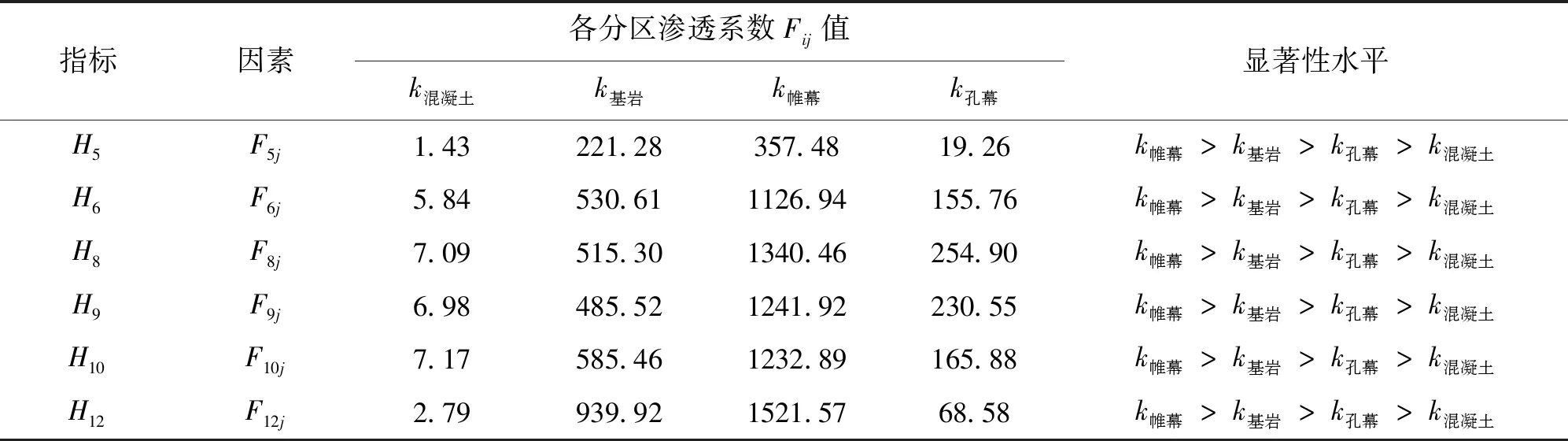
表6 各典型测点指标Hi方差分析结果
基于极差分析和方差分析获得的各因素敏感性和显著性分布规律相同,均为k帷幕>k基岩>k孔幕>k混凝土。各因素对于南北线边坡、闸底板和闸墩间隙等6个典型测点水头值的敏感性趋势相同且各分区渗透系数影响权重随着测点位置的不同而变化,其中k基岩和k孔幕的影响权重随位置变化的幅度较大。综上所述,开展该船闸工程渗透系数反演分析时,应关注帷幕、基岩和孔幕的渗透系数,混凝土的渗透系数可根据经验或参考类似工程选取。
5 参数反演及成果分析
基于船闸枢纽各分区材料渗透系数的敏感性分析,采用可变容差法[19]进行船闸渗透系数的反演计算。具体步骤如下:(1)基于地质勘测数据,初定各分区材料渗透系数的反演范围及初始值;(2)计算船闸渗流场水头分布,提取测点水头计算值,分析与实测值之间的误差是否满足要求;(3)根据上一组误差,修正渗透参数,不断重复上述操作,直到误差满足要求,即可得到计算参数值。
各分区材料的渗透系数反演计算结果见表7;6个典型测点的地下水水位实测值与反演计算值分布趋势及误差分析如图5所示。

表7 各分区材料渗透系数值反演计算结果cm/s
由图5可知,各典型测点地下水水位反演计算值与实测值的相对误差均小于3%,平均相对误差为0.97%,最大相对误差为2.37%,满足工程应用要求[20-21]。表明反演计算获得的船闸枢纽各分区材料的渗透系数与实际基本相符,可用于船闸三维渗流分析。

图5 各典型测点地下水水位反演计算值与实测值对比
图6为船闸基础地下水水位等值线分布图。由图6可知,船闸两岸岩体及闸前基岩水位趋向船闸方面逐渐下降,降幅均匀,两线闸墩处地下水水位等值线分布密集,浸润面变化剧烈,渗透坡降较大;两线船闸底板基岩的地下水水位约为125 m,低于外围水位值。为进一步分析船闸渗流性态,绘制了库水位为174.35 m时水流方向典型剖面水头等势线分布图,如图7所示。由图7可知,船闸底板等部位混凝土结构等势线分布密集,走向趋近于水平,分布规律符合工程实际。综上可知,船闸地下水水位分布规律合理,采用反演得到的计算参数开展船闸三维渗流场模拟,其模拟结果可有效反映船闸混凝土结构、基岩及两岸岩体的渗流特性。
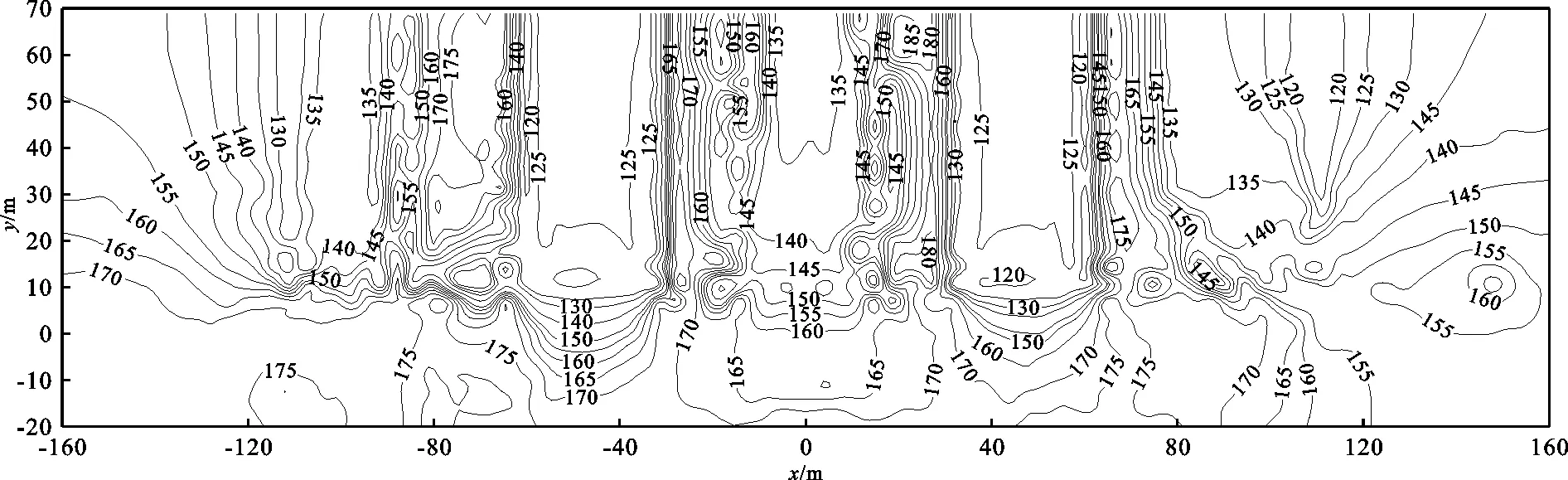
图6 船闸基础地下水水位等值线分布(单位:m)

图7 船闸段典型横断面水头等势线分布(单位:m)
6 结 论
本文针对某船闸枢纽混凝土闸体、基岩、防渗帷幕和排水孔幕的渗透参数开展了敏感性分析及渗透系数反演分析,主要结论如下:
(1)各分区材料渗透系数对船闸地下水水位的影响程度排序为:k帷幕>k基岩>k孔幕>k混凝土;帷幕、基岩和孔幕的渗透系数对船闸渗流场的影响较为显著,开展船闸各分区材料渗透系数反演分析时应重点关注影响程度较大的分区。
(2)采用可变容差法反演计算各分区材料的渗透系数时,应重点对帷幕和基岩的渗透系数进行反演,反演得到其渗透系数分别为3.04×10-6和5.51×10-6cm/s。各典型测点地下水水位反演计算值与实测值的最大相对误差为2.37%,反演结果合理,可作为该船闸枢纽渗流分析的计算参数。
(3)对船闸主要分区材料的渗透系数进行反演时,应结合敏感性分析筛选需重点反演的分区,以提高反演计算效率。本文的研究成果可为类似工程提供借鉴。
