基于IGA-BPNN的水电站厂房振动响应预测

2022-06-30陈金泉王海军刘娟莉

水资源与水工程学报 2022年3期

陈金泉，王海军，刘娟莉，刘通，梁超

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300350；2.天津大学建筑工程学院，天津300350；3.雅砻江流域水电开发有限公司二滩水力发电厂，四川攀枝花 617000)

1 研究背景

基于上述问题，本文依托某一河床式水电站原型观测数据，提出了一种基于IGA (improved genetic algorithm,改良遗传算法)-BPNN(back propagation neural network,BP神经网络)的水电站厂房振动响应预测模型。原型观测实例表明，该预测模型的精度明显高于普通BPNN模型，与GA-BPNN模型对比，IGA-BPNN模型由于对普通遗传算法做了改进，其预测精度与速度也有所提高，可满足实际工程使用的要求。

2 改良遗传算法

遗传算法(genetic algorithm,GA)是人类效仿自然界生物进化机制衍生出来的一种优化算法，具有全局概率搜索且高效并行的特点，广泛应用于组合优化类问题的求解[13]。但普通GA需要预设互换、变异操作概率，容易受人为主观因素的影响，另外在进行选择操作时，会存在某些个体适应度高于平均群体适应度而被大量复制的情况，即出现“近亲繁殖”的现象，将会造成算法早熟收敛问题[14]。

基于此，本文引入了自适应互换、变异机制加以改良，可在群体进化过程中动态调整互换、变异操作概率，克服了人为预设互换、变异操作概率这一缺点。其基本原理是：根据个体适应度与群体整体适应度的相对大小关系，在群体进化过程中动态调整互换、变异操作概率，在保证群体多样性的基础上，保护优质解的结构不被破坏，从而提高了算法的寻优性能[15-17]。

2.1 自适应互换策略

互换操作中的互换概率Pc对遗传算法的寻优性能有着重要影响，若Pc值过大，将会造成染色体适应度变化幅度较大；若Pc值过小，将会造成搜索缓慢甚至算法早熟。为减轻预设互换概率的影响，基于自动调整适应外部环境变化的思想，引入自适应互换概率，其计算公式如下：

(1)

式中:Fc为个体适应度；Fmax为最大群体适应度；Fa为平均群体适应度；Pc max为最大互换概率；Pc min为最小互换概率。自适应互换策略可根据个体适应度与群体整体适应度的相对大小，实现互换概率的自适应调整。当Fc>Fa时，以最小概率Pc min对子代染色体进行扰动，尽可能地保护优质个体；当Fc≤Fa时，Pc随着个体适应度减小而靠近Pc max。

2.2 自适应变异策略

与互换概率类似，变异概率Pm取值是否恰当也会主导寻优结果的好坏。自适应变异概率公式如下：

(2)

式中:Pm max为最大变异概率；Pm min为最小变异概率。与互换概率Pc的改进相近，当Fc>Fa时，以最小概率Pm min对子代染色体进行扰动，尽可能地保护优质染色体；当Fc≤Fa时，Pm随着个体适应度减小而靠近Pm max，经自适应变异操作形成新群体。

3 IGA优化算法函数测试

为了验证IGA的优化效果，根据上文介绍的自适应互换和变异策略原理自编程序，选用业内常用的Sphere、Three-hump Camel(TC)、Griewank和Schaffer函数作为输入进行函数测试。

(1)Sphere函数

(3)

函数定义域为：-100≤xi≤100，在(0,0，…，0)处取得全局最小值为0。

(2)Three-hump Camel函数

(4)

函数定义域为：-5≤xi≤5，-5≤xi+1≤5，在(0,0)处取得全局最小值为0。

(3)Griewank函数

(5)

函数定义域为：-600≤xi≤600，在(0,0，…，0)处取得全局最小值为0。

(4)Schaffer函数

(6)

函数定义域为：-2.048≤xi≤2.048，在(0,0，…，0)处取得全局最小值为0。

测试计算结果如表1所示。

表1 各函数的测试结果分析

由表1可以看出，从计算复杂度较低的单峰函数到复杂度较高的多峰函数，IGA的全局搜索和优化表现均优于GA，平均耗时短，克服了普通GA适应度函数收敛速度慢的缺点，也从侧面验证了该算法具有良好的鲁棒性。

4 基于IGA-BPNN的预测模型

BPNN各层由权重值和阈值相连接，网络训练的过程实际上就是调整网络权重值和阈值这两个参数的过程。BPNN训练结果的好坏很大程度上取决于初始权重值和阈值的质量，单一的BPNN模型需要预设这两个初始参数，极易受主观经验影响，引入IGA对BPNN的初始权重值和阈值进行优化，充分发挥IGA高效并行、全局搜索的特点，建立基于IGA-BPNN的预测模型，解决了BPNN之前存在的训练参数难确定、精度差、效率低等问题。具体操作流程如图1所示。

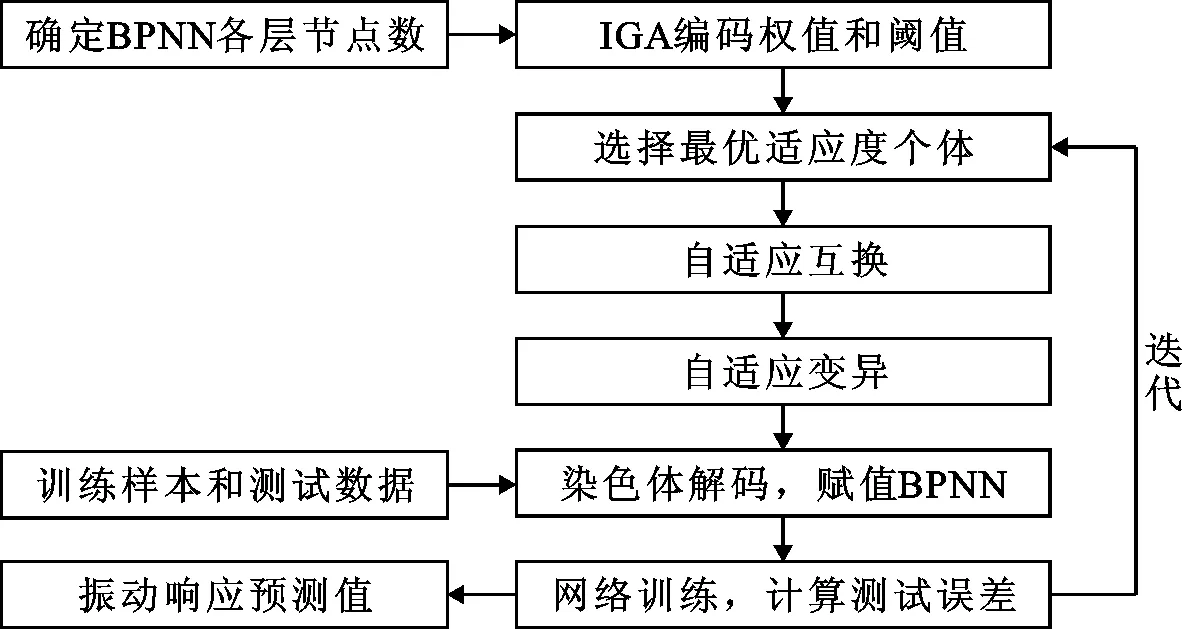
图1 基于IGA-BPNN的振动响应预测模型运行流程图

5 实例分析

结合某一河床式水电站工程实例，运用基于IGA-BPNN的预测模型对其结构振动响应进行预测研究。原型观测采用DP型低频位移振动传感器，采样频率为200 Hz，采样时长为300 s，将原型观测数据经过降噪、滤波处理后得到的位移双幅值作为预测模型的输入数据，测试工况选取4孔泄洪闸开度相同、4#机组负荷在60～120 MW的稳定运行区间，工况信息与各测点位移双幅值数据如表2、3所示，水电站厂房结构及机组测点布置如图2所示。

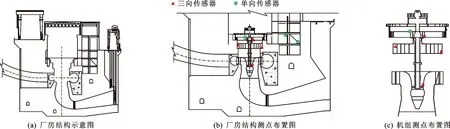
图2 实例河床式水电站厂房结构及振动测点布置

5.1 预测模型创建

分析表2、3数据可知，工况1～4泄洪闸4个闸门开度保持不变、4#机组稳定运行负荷从60 MW逐步上升到120 MW时，机组厂房结构观测部位的振动位移基本呈增大趋势，其中横河向振动位移变化最明显；分别从工况2、5、8和工况3、6以及工况4、7来看，当4#机组稳定运行负荷相同、4个闸门开度从4.7 m增至6.0 m时，机组厂房结构观测部位的振动位移也大致呈增大趋势，其中厂房结构的振动位移变化最明显；无论是机组负荷增大还是闸门开度增大的工况，均存在个别部位振动位移先增大后减小或者先减小后增大的现象，这也验证了前文提到的厂房结构振动体系具有的随机性、非线性特点，说明所取数据具有代表性。

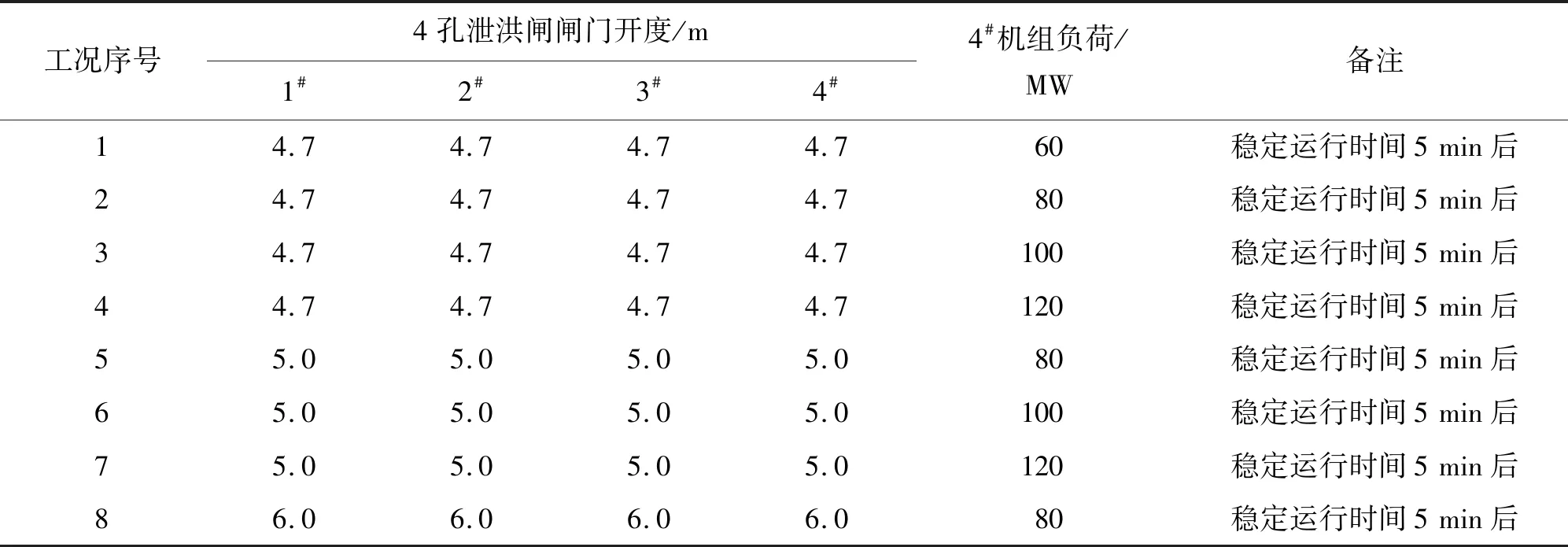
表2 厂房结构振动响应测试工况

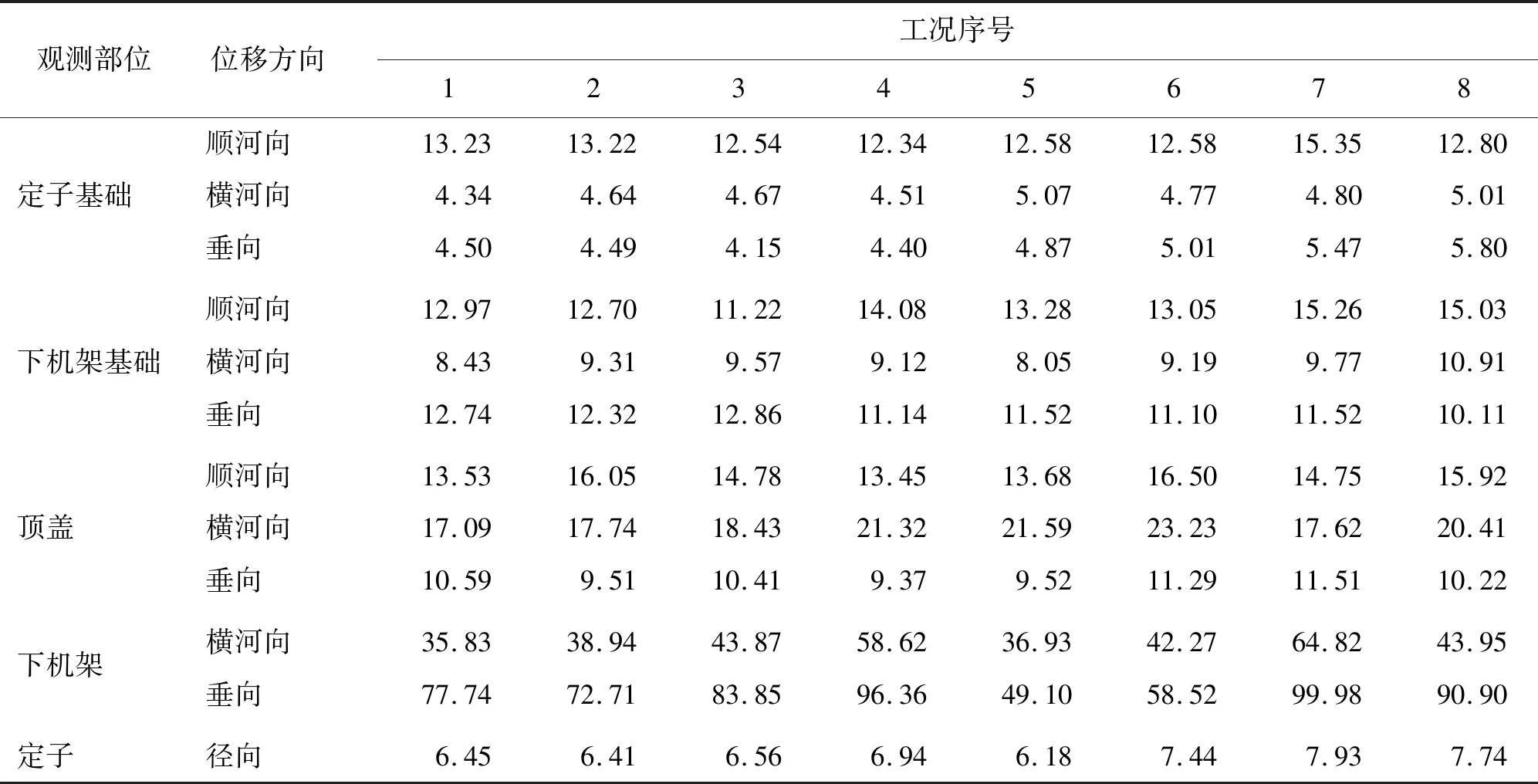
表3 各工况厂房结构观测部位振动位移双幅值数据 μm

IGA-BPNN模型的输入、输出节点数量由训练样本的特征维数决定。河床式水电站厂房上游面直接挡水，在泄洪闸开闸泄洪时，受到尾水绕流的影响，同时又作为机组的支撑结构，受到多振源的直接作用。故选取最能代表厂房机组耦合振动情况的定子基础、下机架基础、顶盖等部位的原型观测数据作为输入，输入层节点数为12，选取其中的定子基础和下机架基础部位的振动位移作为输出，输出层节点数为4。根据经验公式[18]，隐藏层节点数确定为2。

通过预处理将数据分为训练与测试两部分。训练数据用于模型的创建及神经网络的训练，测试数据则用来核验预测模型的结果和误差分析。其中检验测试数据随机采用工况7相对应的数据，训练数据采用其他工况相对应的数据。模型参数设置见表4，其中训练次数、进化次数、群体大小等参数的设置是在参照类似应用遗传算法和神经网络研究的基础上，经试算比较后确定[16-17]。

表4 厂房结构振动位移各预测模型参数设置

5.2 预测结果分析

IGA-BPNN与GA-BPNN目标函数值随迭代次数的变化如图3所示，水电站厂房结构预测所选部位振动位移的不同模型预测结果及分析如图4和表5所示。

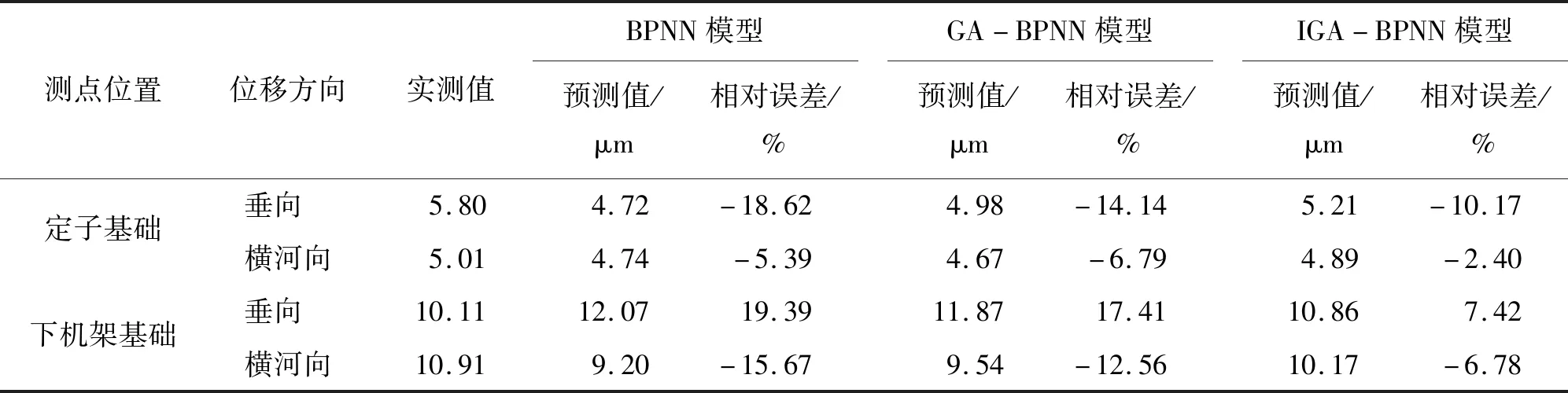
表5 厂房结构预测所选部位振动位移的不同模型预测结果分析

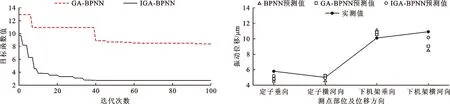
图3 IGA-BPNN与GA-BPNN目标函数值随迭代次数的变化图4 厂房结构预测所选部位振动位移的不同模型预测结果与实测值比较

由图3可知，IGA不仅可以更快速地找到网络最优权重值和阈值，而且寻优结果的质量优于GA。由图4和表5中的预测结果可知，基于IGA-BPNN预测模型的精度显著高于BPNN和GA-BPNN预测模型。IGA-BPNN模型的预测位移值均不超过0.15 mm，根据最新的水电站厂房设计规范[19]，针对机墩这类特殊结构，其振动位移的控制标准是竖向振幅小于0.15 mm，水平横向与扭转振幅之和小于0.20 mm，预测结果全部满足规范要求。结构振动位移实测最大值为1.09×10-2mm，模型预测相对误差均小于11%，即模型预测最大误差绝对值不超过1.20×10-3mm，仅为规范要求数值的0.81%，故可用于实际水电站厂房振动响应预测。

由于遗传算法和神经网络属于概率型算法，每次寻优结果会有些许不同。通过决定系数R2、平均绝对误差MAE以及均方根误差RMSE从不同维度来衡量实际预测效果，一般来说决定系数R2的大小可以反映出预测值与实测值的相关性，即R2越大，则两者的相关性越好；预测精度直接与MAE和RMSE呈负相关，即MAE和RMSE越小，则预测精度越高。各模型预测结果的统计计算分析见表6。

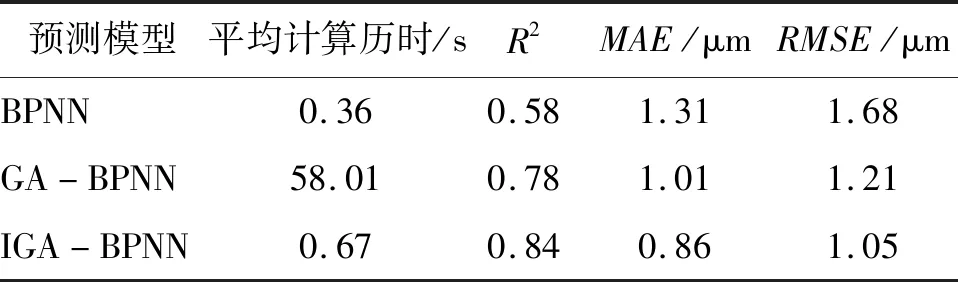
表6 各模型预测结果的统计计算分析

由表6可知，3种模型预测结果的R2均大于0.55，其中GA-BPNN和IGA-BPNN模型预测结果的R2较BPNN模型有较大提升，说明利用GA对BPNN的权重值和阈值进行优化可以显著改良预测模型；通过对比GA-BPNN模型与IGA-BPNN模型的统计参数表明，对普通GA进行改进有利于提高整个预测模型的性能。从误差来看，IGA-BPNN模型的预测效果是最优的；从计算历时来看，IGA-BPNN模型在提高预测精度的前提下，所消耗的平均计算时间远小于GA-BPNN模型，且计算代价相较于BPNN模型也增加不大。