无人机机载振动测量系统与数据归纳方法研究★
2022-06-30王妙纪春阳杨剑锋吴其琦蔡茗茜吴和龙
王妙,纪春阳,杨剑锋,3,吴其琦,蔡茗茜,3,吴和龙,3
(1.广州赛宝腾睿信息科技有限公司,广东 广州 511370;2.工业和信息化部电子第五研究所,广东 广州 511370;3.广东省无人机可靠性与安全性工程技术研究中心,广东 广州 511370;4.广西科技大学,广西 柳州 545006)
0 引言
无人机在飞行过程中由发动机产生的振动会极大地影响飞控系统上搭载的传感器测量精度及吊舱上光学载荷的成像质量,同时机上振动也会造成无人机结构疲劳损伤,因此,在无人机的研发及交付过程中需要开展振动环境试验,以此验证无人机的振动环境适应能力和耐久性水平。现有的标准没有针对无人机飞行工况的振动载荷谱,而有人机与无人机无论在技术上,还是在结构、强度、任务剖面和环境剖面等方面都存在较大的差异,因此也无法参考有人机的振动载荷谱。为了提高无人机振动环境试验与实际使用剖面的相似性,需要设计出机载轻量化振动测量系统和振动数据归纳方法。
国内无论军用标准还是民用标准都有介绍振动载荷谱编制的方法,其中,GJB/Z 126—99[1]规定了振动与冲击环境测量数据的归纳方法;GB/T 4797.9—2021[2]提出一种在贮存、运输和使用过程中测得的振动与冲击数据的归纳方法。田永卫等人[3]根据某型飞机测得的振动数据,基于现有的国军标和相关标准,提出以分测试区域不同状态下的振动规范谱编制归纳方法。高文涛等人[4]介绍了一种空勤人员位置处的1/3倍频程振动谱的归纳方法,并将这种方法得到的结果与常规方法进行了对比。杨梅等人[5]将时域分析的思想引入到机载设备可靠性振动试验的归纳方法中,提出可靠性振动试验谱型和试验时间的编制方法。雷晓波等人[6]基于现有的国军标和数理统计原理,给出了振动数据归纳流程中若干环节的具体实现方法,建立了周期振动和随机振动试飞数据的归纳方法。以上文献涉及的振动测试数据归纳方法皆以有人机为对象,针对具体的应用场景和任务需求而提出,不一定适用于无人机。本文研究对象为无人机,关注重点为机载振动对飞控系统性能的影响,基于以上研究方法提出一种无人机机载振动测量系统及振动载荷谱编制归纳的方法,为无人机振动试验剖面的制定提供工程化解决方案。
1 无人机机载振动测试系统
由于民用轻小型无人机载重小,且存放负载空间有限,因此市场上常见的商用振动测试系统难以满足无人机振动的测试需求,基于此,本研究开发出图1所示的无人机机载振动测试系统。该振动测试系统由供电锂电池、振动数据采集模块、温度传感器、温度传感器线盒、振动传感器接线和加速度传感器等组成。振动数据采集模块的基本参数如表1所示,包含12个振动数据测试通道和1个温度测试通道。如果只需要测试振动数据,则不需要接入温度传感器接线盒和温度传感器等,从而减轻飞行重量。

图1 无人机机载振动测试系统

表1 机载振动测试系统的主要功能性能参数
机载振动测试系统采用“上位机-采集模块-传感器”的3层式结构,如图2所示。数据采集模块是测量系统的中心,向下接入4个3轴加速度传感器与1个温度传感器,实现振动信号的采集与存储;向上通过无线串口与上位机通信。传感器采用2线接口方式的加速度传感器,内含X、Y、Z 3个测量轴。上位机运行采集软件,实现参数设置、波形显示和控制主机等功能。

图2 机载振动测试系统结构
2 无人机发动机振动数据采集
用于振动测试的被试无人机为TX25A型垂直起降无人机,具体的参数如表2所示。机载振动测试系统固定在机内中舱,三向加速度传感器安装在发动机固定座上,如图3所示。机载振动测试系统的采样频率为4.8 kHz,采样时间为41 s,采样点数为196 800个,发动机X、Y、Z 3个方向的振动测试时域曲线如图4所示。

表2 TX25A型垂直起降无人机参数

图3 机载振动测试系统安装图
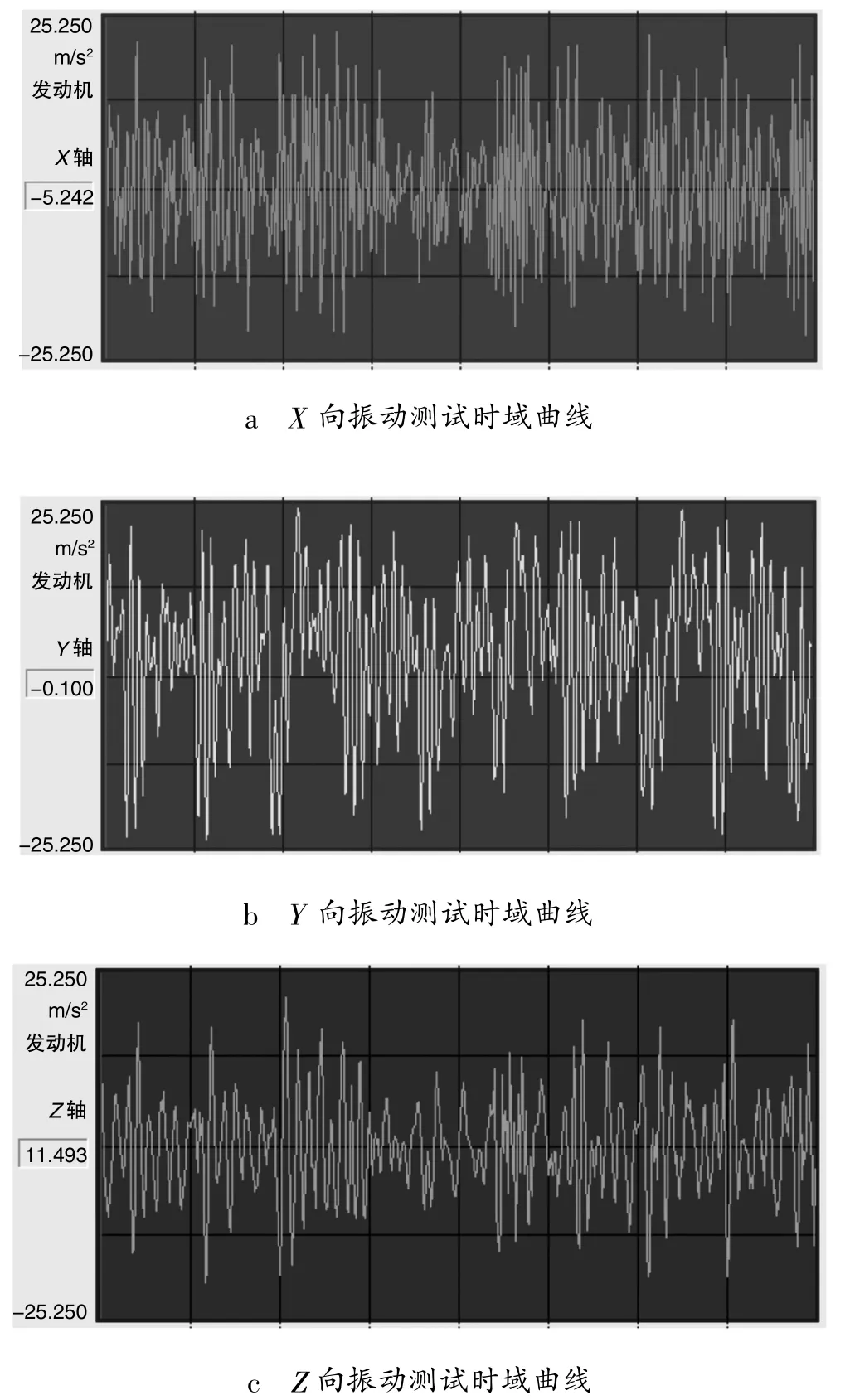
图4 TX25A型垂直起降无人机发动机振动测试时域曲线
3 振动测试数据处理
3.1 多项式趋势消除
机载振动测试系统采集到的振动数据,由于放大器随温度变化产生的零点漂移、传感器频率范围外低频性能的不稳定和传感器周围的环境干扰,往往会偏离基线,甚至偏离基线的大小还会随时间变化。偏离基线随时间变化的整个过程被称为信号的趋势项。趋势项直接影响信号的正确性,应该将其剔除。
令测试得到的振动时域信号为[x1x2…xk]T(k=1,2,3,…,n),采样时间间隔Δt=1/4 800 s。基于最小二乘法,消除线性趋势项的计算公式可表达为:

其中,yk——消除多项式趋势后的时域信号,a0和a1的表达式为:

3.2 平滑处理
机载振动采集系统采样得到的振动数据往往叠加有噪声信号。噪声信号除了有50 Hz的工频及其倍频程等周期性的干扰信号外,还有不规则的随机干扰信号。由于随机干扰信号的频带较宽,有时高频成分所占的比例较大,使得测试得到的时域曲线呈现很多毛刺、不光滑。为了削弱干扰信号的影响,需要对采样数据进行平滑处理。五点三次平滑法利用最小二乘法原理对离散数据进行三次最小二乘,计算公式为:
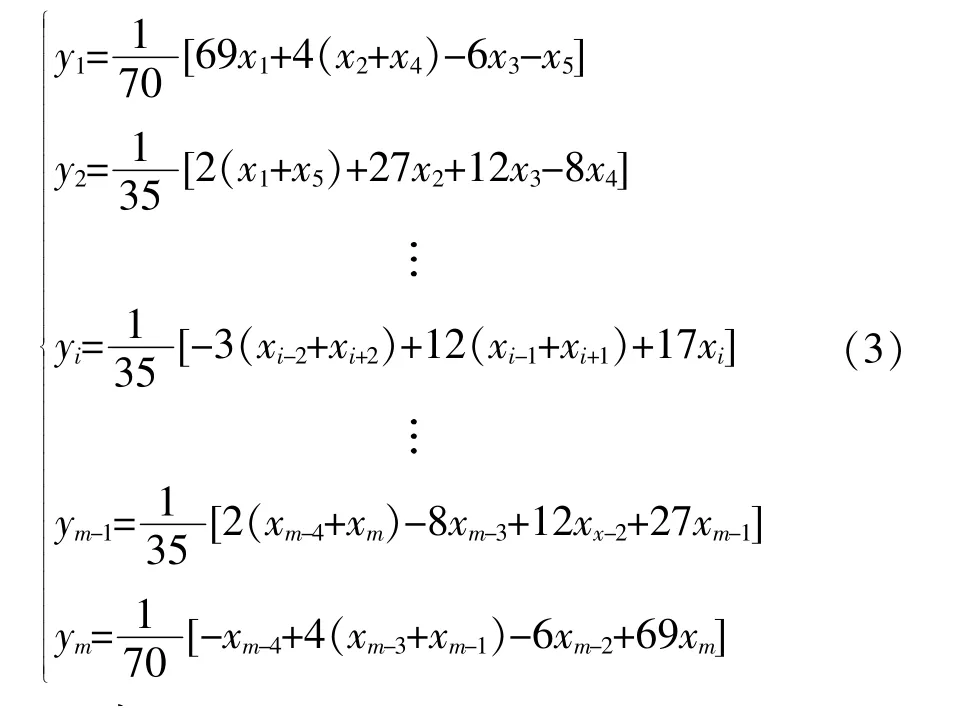
式(3)中:i=3,4,…,m-2。
3.3 频谱变换
对采集到的原始振动时域信号消除多项式趋势和平滑处理,然后进行频谱变换,将时域信号进行频谱变换获得振动信号每条谱线的功率谱密度值。本研究采用MATLAB数值分析软件中的Welch法功率谱估计函数pwelch()进行功率谱密度的求解,在频谱变换过程中使用汉宁窗函数hanning()。
4 振动载荷谱归纳
4.1 PSD谱假设检验
根据GB/T 4797.9—2021,螺旋桨式飞行器的振动信号服从对数正态分布。对PSD谱进行对数变换,并进行卡方检验是否服从正态分布。根据GJB/Z 126—99的要求,测量数据的统计学自由度需大于45°,将X、Y、Z 3个方向的振动采集数据分别等分为46个小样本,每个样本的数据量为4 096个。利用MATLAB中的卡方检验函数chi2gof()进行检验,得到X、Y、Z 3个方向分别有374、386、364条谱线的数据无法采用,对不满足要求的数据进行删除。
4.2 PSD谱归纳方法
采用正态容差限对PSD谱进行归纳,通过以下公式进行转换:

式(4)中:x——PSD谱的纵坐标值,即谱值;
y——谱值的对数。
y的正态容差限(NTL)定义为:对于y的所有可能取值,在γ置信度下,能够覆盖集合y的100β%数据的置信上限,可由下式给出:

Sy——样本标准差;
C——正态容差因子。
通过查表,在样本量为46个,置信度为50%,覆盖95%的条件下,正态单边容差因子值为1.66。
PSD谱的正态单边容差限可以通过以下公式计算得到:

TX25A型垂直起降无人机振动测试数据PSD谱在50%置信度和95%覆盖条件下的正态容差包络曲线如图5所示。

图5 无人机振动测试数据PSD的95/50NTL包络线
4.3 振动载荷谱平滑处理
对于试验室振动试验,图5中所示的曲线无法直接被使用,因此需要进行进一步的平滑处理,得到可以用于振动台的振动载荷谱。本研究采用倍频程平均法,结果表明,采用1/3倍频程平均的断点数量能够与整体形状形成最佳匹配,故选择1/3倍频程。
选用1 000 Hz为基准频率,以2为基数,1/3倍频程的中心频率为:

式(8)中:fu——倍频程带上边界;
fl——倍频程带下边界。
取倍频程带宽内的所有频率点的纵坐标的平均值,作为功率谱密度值。采用标准斜率绘制振动载荷谱,采用12 dB/oct或6 dB/oct的倍数作为斜率,可以得到标准斜率1/3倍频程平均法下的振动载荷谱曲线,如图6所示。
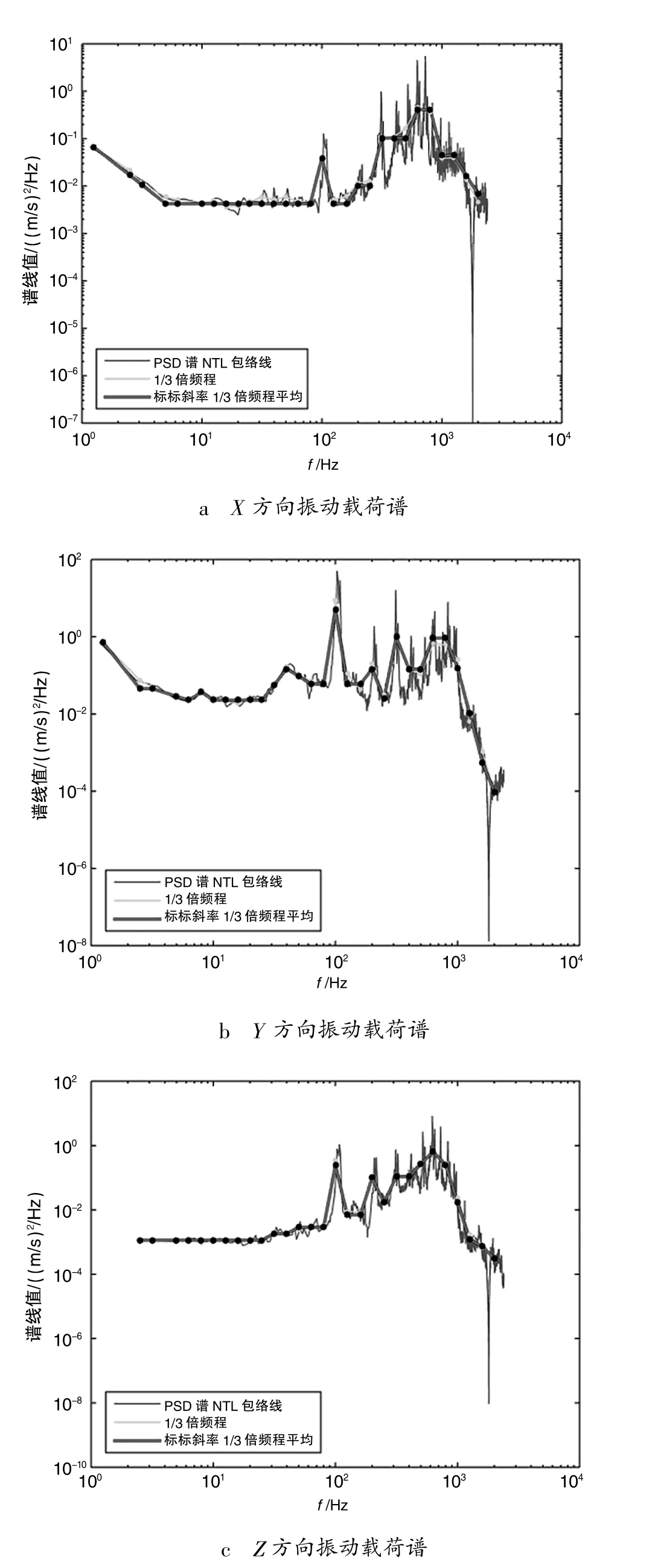
图6 TX25A型垂直起降无人机发动机振动载荷谱
5 结束语
本文提出了一种结构紧凑的机载轻量化振动测量系统,对该测量系统的主要功能性能参数及指标进行了介绍。利用该测量系统对TX25A型垂直起降无人机发动机安装面的振动进行了测量。基于测得的振动数据,给出时域信号的处理方法及利用MATLAB数值分析软件对测得的振动数据进行频谱变换。提出针对功率谱密度谱的归纳方法,该方法基于统计学原理,采用正态容差法,通过对功率谱密度值进行对数正态变换,考虑正态容差因子的影响,编制标准斜率下的无人机发动机振动载荷谱。本文给出了实现振动载荷编制的MATLAB方法,利用该方法可以快速地对测得的振动数据进行载荷谱的编制,实施简单、工程化强,具有实际的工程意义。
